Grandezze alternate sinusoidali

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Elettrotecnica

Grandezze alternate sinusoidali

Sono grandezze (nel caso di circuiti elettrici tensioni e correnti) che variano nel tempo secondo la legge:

y(t) = Y_M·sen(w·t + a_O)

rappresentabile anche graficamente:

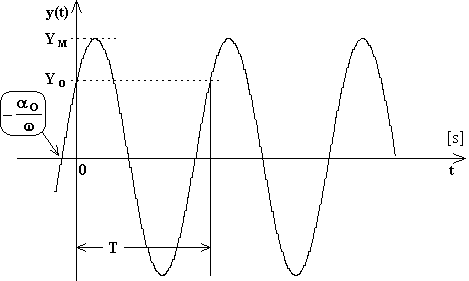
Si tratta di grandezze periodiche in quanto riassumono sempre lo stesso valore ad istanti di tempo tra di loro intervallati di K·T [s] con K = ±1 , ±2 , ... ove T [s] è detto periodo.

Si tratta di grandezze alternate in quanto, considerato un intervallo qualsiasi di tempo di ampiezza pari al periodo T , l'area sottesa dalla parte positiva della funzione è uguale all'area sottesa dalla parte negativa della funzione. Per tale motivo si dice che il valore medio in un periodo è nullo.

I valori caratterizzanti di una grandezza che varia sinusoidalmente nel tempo sono:

a) Il valore massimo Y_M ;

b) Il periodo T [s] ;

c) La frequenza f = 1 / T [Hz] che rappresenta il numero di sinusoidi al secondo;

d) La pulsazione:

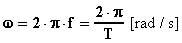
e) L'argomento iniziale a_O [rad];

f) Il valore iniziale Y_O;

g) Il valore medio in un semiperiodo:

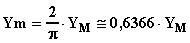
che rappresenta l'altezza del parallelogramma di base T / 2 affinché l'area del parallelogramma stesso sia uguale all'area sottesa da un'intera semionda positiva;

h) Il valore efficace:

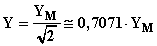
che, matematicamente, ha il significato di radice quadrata del valore medio in un periodo dei quadrati dei valori istantanei (più avanti esamineremo il suo significato fisico);

i) Il fattore di forma:

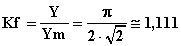
Grandezze alternate sinusoidali e vettori ruotanti

E' possibile creare una corrispondenza biunivoca tra i vettori ruotanti e le grandezze sinusoidali. Questo significa che le grandezze sinusoidali possono essere raffigurate come vettori ruotanti:

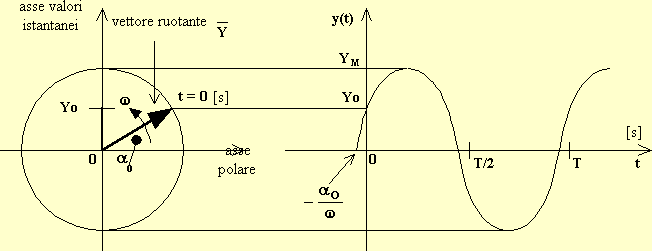
La figura rappresenta il vettore ruotante 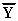a_O) , ovvero y(t). Convenzionalmente, gli angoli si intendono positivi se misurati in senso antiorario.

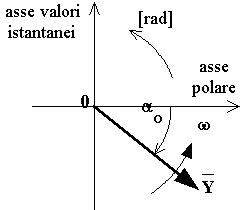
La figura sopra mostra la rappresentazione mediante il vettore ruotante di una grandezza sinusoidale che ha un argomento iniziale negativo ( pari a - a_O).

L'espressione analitica, sul piano di Gauss, del generico vettore ruotante è:

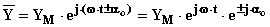
Dove e^j·^w·t è il termine che determina la rotazione.

Le grandezze sinusoidali (tensioni e correnti) nei circuiti che noi studiamo sono tutte isofrequenziali, questo significa che tutti i vettori ruotanti che le rappresentano ruotano alla medesima velocità angolare w [rad/s]. Per tale motivo i vettori ruotanti conservano nel tempo una posizione reciproca costante, quindi è sufficiente rappresentarli nella posizione che essi occupano all'istante t = 0 [s]. A questo punto, per rappresentare una grandezza sinusoidale è sufficiente un vettore statico e, per il suo trattamento analitico, l'equivalente numero complesso.

Nella figura seguente sono rappresentate due grandezze sinusoidali y_A(t) ed y_B(t) :

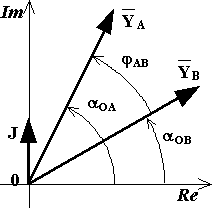
y_A(t) = Y_MA·sen(w·t + a_OA) , y_B(t) = Y_MB·sen(w·t + a_OB)

mediante i corrispondenti vettori 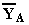w). Nella rappresentazione è omessa l'informazione riguardante il fatto che i vettori sono ruotanti e gli stessi sono riportati nella posizione assunta all'istante t = 0 [s]. Il piano di Gauss è il luogo ove rappresentare in forma grafica i numeri complessi, più precisamente l'ascissa diventa l'asse dei valori reali Re mentre l'ordinata diventa l'asse dei valori immaginari Im.

Gli angoli a_OA ed a_OB sono gli argomenti iniziali delle grandezze sinusoidali, servono per orientare i vettori rappresentativi delle grandezze sinusoidali sul piano di Gauss e vengono riportati a partire dal semiasse reale positivo seguendo la nota convenzione secondo la quale gli angoli si intendono positivi se misurati in senso antiorario (convenzione che discende direttamente da quella, già dichiarata, per la quale il verso di rotazione dei vettori ruotanti è antiorario).

L'angolo j_AB rappresenta lo sfasamento tra la grandezza sinusoidale y_A(t) e la y_B(t). Analiticamente si ha:

j_AB = a_OA - a_OB , j_BA = a_OB - a_OA , j_AB = - j_BA

Circuito puramente resistivo in regime sinusoidale, potenza attiva

E' così chiamato un circuito totalmente privo di effetti d'autoinduzione dovuta a campi magnetici variabili e di accumulo di carica dovuta a campi elettrici.

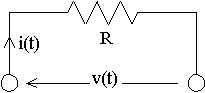
Sollecitando la resistenza R [W] con una corrente sinusoidale i(t) [A] si avrà (legge di Ohm) per ogni istante t ai capi della resistenza una caduta di tensione pari a v(t) = R·i(t) [V] pure essa sinusoidale, di eguale pulsazione, di eguale argomento iniziale e di valore massimo V_M = R·I_M [V].

Per quanto riguarda i valori efficaci si avrà la relazione V = R·I [V].

Siccome gli argomenti iniziali della tensione e della corrente sono gli stessi, si suole dire che esse sono tra di loro in fase.

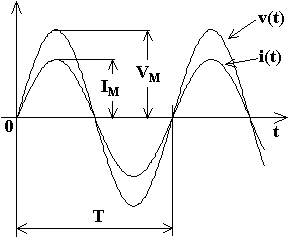
Facendo riferimento ad una corrente sinusoidale qualsiasi, per l'espressione ai valori istantanei si avranno le seguenti relazioni:

i(t) = I_M·sen(w·t + a_O) , v(t) = V_M·sen(w·t + a_O) [A]

Per l'espressione simbolica si avrà:

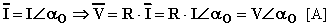
Per quanto riguarda la potenza, applicando la legge di Joule in ogni istante t si può calcolare come varia la potenza istantanea p(t) facendo il prodotto dei valori istantanei i(t) e v(t).

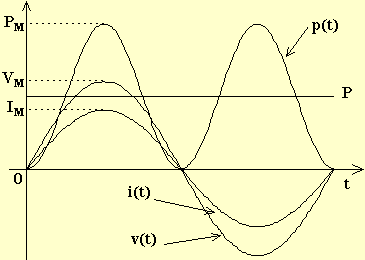
Dal grafico che così si ottiene si osserva che la potenza p(t) è una grandezza periodica (non sinusoidale) pulsante, sempre maggiore di zero,di frequenza doppia di quella della corrente. Sempre dal grafico si può osservare che il valore medio P [W] della p(t) è la metà del suo valore massimo P_M , ovvero:

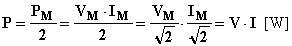
L'area sottesa dalla forma d'onda di p(t) rappresenta in un determinato intervallo di tempo l'energia ( [W]·[s] = [J] ) e tale energia è sempre positiva, questo significa che nella resistenza avviene una trasformazione di energia sempre nel senso energia elettrica Þ calore. Per tali motivi P prende il nome di potenza attiva (cioè ad essa corrisponde una effettiva trasformazione di energia). Ricordando la legge di Ohm, la potenza attiva si può anche calcolare con le relazioni:

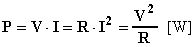
Circuito puramente induttivo in regime sinusoidale

E' tale un circuito totalmente privo di resistenza ohmica e di accumulo di carica dovuto a campi elettrici. L'unico parametro elettrico che caratterizza un circuito puramente induttivo è perciò la sua induttanza. L'induttanza (chiamata pure coefficiente di autoinduzione) è definita dal rapporto tra il flusso di campo magnetico (originato dalla corrente che percorre il circuito) che si concatena col circuito e la corrente che percorre il circuito stesso:

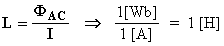
Il valore di induttanza di un circuito dipende dalla geometria del circuito e dalla permeabilità magnetica del mezzo che circonda il circuito: se queste sono costanti, l'induttanza è costante. Per tale motivo, l'induttanza di un circuito avvolto su di un nucleo ferromagnetico non è costante ma varia al variare della corrente nel circuito in quanto al variare della corrente varia il campo magnetico e, con esso, la permeabilità (noi, comunque, considereremo costante l'induttanza). Invece, l'induttanza di un circuito in aria è rigorosamente costante essendo costante la permeabilità magnetica dell'aria.

Si supponga di avere un circuito puramente induttivo, di induttanza costante L [H], percorso da una corrente sinusoidale i(t) = I_M·sen(w·t) [A]. A causa della induttanza L, si autoconcatenerà col circuito un flusso:

f_A_C(t) = L· i(t) = L·I_M· sen(w·t) = F_ACM· sen(w·t) [Wb]

con F_ACM = L·I_M [Wb]. Ovviamente tale f_A_C(t) , essendo proporzionale in ogni istante alla corrente, varierà esso pure nel tempo con legge sinusoidale.

Per via della legge generale dell'induzione elettromagnetica, la variazione nel tempo del flusso autoconcatenato produrrà una forza elettromotrice autoindotta di valore:

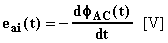
che gode delle seguenti proprietà:

a) e_ai(t) è proporzionale alla rapidità con cui varia il flusso concatenato nel tempo;

b) e_ai(t) ha in ciascun istante un verso tale da opporsi alla causa che la genera, perciò sarà contraria alla corrente quando questa aumenta facendo aumentare f_A_C(t) , mentre avrà lo stesso verso della corrente quando questa diminuisce facendo diminuire f_A_C(t).

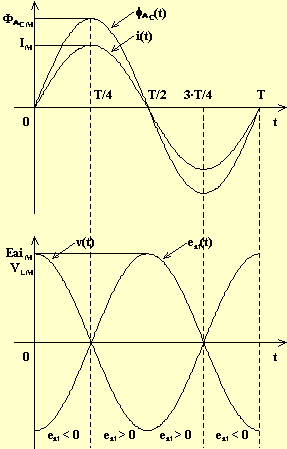
Dal secondo punto si determina immediatamente il segno della f.e.m.a.i., dal primo punto si determina la sua intensità che è nulla quando la pendenza della i(t) , e quindi di f_A_C(t) , è nulla (vedi gli istanti T/4 , 3·T/4 ), mentre è massima quando la pendenza della i(t) , e quindi di f_A_C(t) , è massima (vedi gli istanti 0 , T/2 ,T ).

Il risultato che si ottiene è una f.e.m.a.i. sinusoidale ed in ritardo di un quarto di periodo (ovvero p/2 ) rispetto sia al flusso che alla corrente:

Inoltre, qualitativamente, si può pure affermare che il valore massimo di f.e.m.a.i. sarà tanto più grande quanto più è grande il valore massimo del flusso e quanto più rapida è la variazione di f_A_C(t) nel tempo (cioè quanto più è grande la sua pulsazione w):

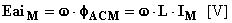
Abbiamo fino ad ora dedotto quanto vale la f.e.m.a.i. dovuta ad una corrente sinusoidale circolante in un circuito puramente induttivo, supponiamo ora che la corrente i(t) venga impressa nel circuito puramente induttivo da un generatore sinusoidale.

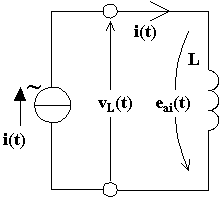
Applicando la legge di Ohm generalizzata all'intero circuito (generatore più resistenza) e facendo riferimento ai valori istantanei si deduce che dovrà essere in ogni istante nulla la somma algebrica della tensione v_L(t) ai capi dell'induttanza e della forza elettromotrice indotta e_ai(t) :

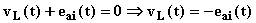
cioè la tensione v_L(t) è in ogni istante uguale ed opposta alla f.e.m.a.i. e_ai(t). Ciò significa (vedi anche il grafico):

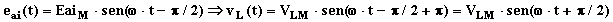
dove ovviamente V_LM = Eai_M. Confrontando con i(t), si dirà che la tensione v_L(t) ai capi dell'induttanza è in anticipo di p/2 ed il suo valore massimo vale .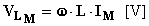

Passando dall'espressione delle grandezze sinusoidali nella forma di valori istantanei alla forma simbolica (vettori ruotanti e relativi numeri complessi) quanto ottenuto può essere così riassunto:

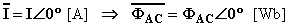
con F_AC = L·I [Wb] ( F_AC ed I valori efficaci ).

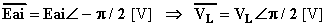
con Eai = V_L = w·L·I [V].

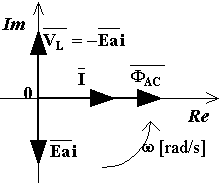
La quantità:

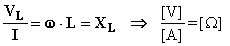
è chiamata reattanza induttiva ed ha le dimensioni di una resistenza. La quantità 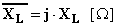è chiamata reattanza induttiva immaginaria ed è un operatore vettoriale in quanto se applicato al numero complesso rappresentante la corrente fornisce il numero complesso rappresentante la tensione ai capi dell'induttanza:

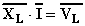
La figura riportata sopra mostra le varie grandezze sinusoidali prese fino ad ora in considerazione rappresentate sul piano di Gauss.

Circuito puramente capacitivo in regime sinusoidale

E' così chiamato un circuito totalmente privo di resistenza ohmica e di effetti d'autoinduzione dovuti a variazioni di campi elettromagnetici. L'unico parametro elettrico che caratterizza un circuito puramente capacitivo è la sua capacità elettrica. La capacità del circuito rappresenta l'attitudine del circuito ad accumulare carica elettrica quando nel dielettrico circostante sia presente un campo elettrico. Se V è la d.d.p., Q la carica accumulata, C la capacità elettrica, si ha:

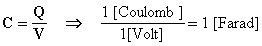
Al fine di dedurre il comportamento della capacità in regime sinusoidale, è importante ricordare il fenomeno della carica e della scarica del condensatore facendo particolare attenzione al verso della corrente i(t) e della tensione v_C(t) ai capi del condensatore:

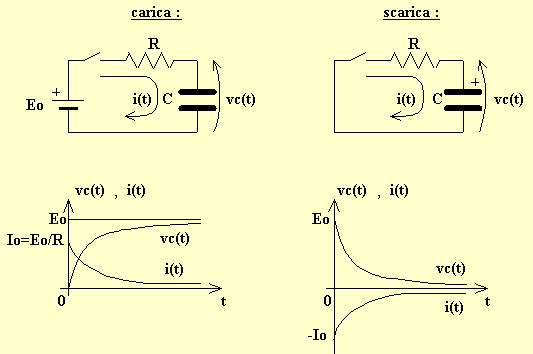
N.B.: l'istante t = 0 [s] coincide, sia per la carica che per la scarica all'istante di chiusura dell'interruttore nel relativo circuito. Le varie funzioni v_C(t) ed i(t) sia nella carica che nella scarica sono di tipo esponenziale, con costante di tempo pari a R·C [s] e quindi con un tempo d'esaurimento pari a circa 5·R·C [s]. Nel caso di circuito in corrente continua, in ogni caso, una volta esauritosi il transitorio la corrente nel circuito è identicamente nulla in quanto il condensatore costituisce a regime un'interruzione del ramo ove si trova inserito.

Supponiamo ora di avere un condensatore di capacità C, inizialmente scarico, collegato ai morsetti di un generatore di tensione sinusoidale v(t). Vediamo di ricavare qualitativamente l'andamento della corrente. Le considerazioni che seguono sono conseguenti al fatto che:

a) durante gli intervalli di carica la corrente deve avere lo stesso verso (segno) della tensione, mentre durante gli intervalli di scarica la corrente è opposta alla tensione;

b) la corrente ha modulo massimo quando inizia la carica, nullo quando la tensione di carica raggiunge il massimo.

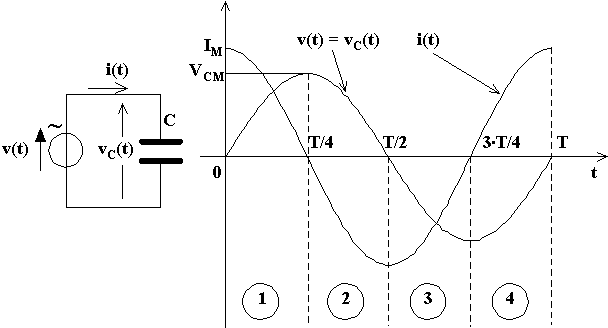
Nel primo quarto di periodo (1), avendosi un intervallo di carica la tensione aumenta positivamente da zero al valore massimo V_CM , il condensatore deve corrispondentemente assorbire una corrente di carica positiva, la quale parte dal suo valore massimo I_Me va poi gradatamente diminuendo fino a ridursi a zero nell'istante in cui il condensatore raggiunge il suo stato di massima carica.

Nel secondo quarto di periodo (2), trattandosi di un intervallo di scarica la tensione alle armature diminuisce da V_CM a zero, il condensatore dovrà corrispondentemente scaricarsi mediante una corrente analoga alla precedente ma di verso (segno) opposto e perciò negativa.

Nel terzo quarto di periodo (3), trattandosi di un intervallo di carica di segno opposto a quello della fase (1), la tensione alle armature aumenterà da zero a -V_CM ed il condensatore sarà interessato da una corrente di carica che varierà da -I_M a zero.

Nell'ultimo quarto di periodo (4), trattandosi di un intervallo di scarica la tensione alle armature diminuirà in valore assoluto da |-V_CM| a zero e la corrente dovrà variare analogamente a quanto avvenuto nell'intervallo (3) ma con verso (segno) opposto.

E' importante osservare che la tensione ai capi del condensatore è obbligata ad essere uguale a quella sinusoidale del generatore, cioè deve essere v(t) = v_C(t) e che la corrente, sia durante gli intervalli di carica che di scarica, non potrà variare con legge esponenziale essendo sia la carica che la scarica non libere ma vincolate dalla tensione sinusoidale presente ai capi del condensatore. Quindi anche la corrente i(t) sarà sinusoidale.

Si riconosce in tal modo che mentre la tensione alle armature del condensatore varia secondo la funzione sinusoidale v_C(t) , la corrente attraverso il condensatore varia secondo una funzione i(t) pure sinusoidale, ma sfasata di un quarto di periodo in anticipo rispetto alla tensione. In forma analitica:

v_C(t) = V_CM·sen(w·t) [V] , i(t) = I_M·sen(w·t + p/2) [A]

Si può poi dimostrare che è I_M= w·C·V_CM [A] ed analoga relazione vale per i valori efficaci. Intuitivamente si può infatti osservare che tanto più grandi sono C e V_CM , tanto più grande sarà la quantità di carica accumulata sulle armature del condensatore. Inoltre la variazione nel tempo della quantità di carica accumulata rappresenta l'intensità della corrente e, perciò, se è elevato w sarà più grande la corrente essendo più grande la variazione di carica nel tempo.

Passando dall'espressione delle grandezze sinusoidali nella forma di valori istantanei alla forma simbolica (vettori ruotanti e relativi numeri complessi) quanto ottenuto può essere così riassunto:

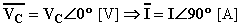
con V_C[V] ed I [A] valori efficaci.

La quantità:

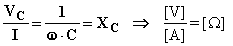
è chiamata reattanza capacitiva ed ha le dimensioni di una resistenza. La quantità 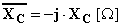è chiamata reattanza capacitiva immaginaria ed è un operatore vettoriale in quanto se applicato al numero complesso rappresentante la corrente fornisce il numero complesso rappresentante la tensione ai capi del condensatore:

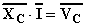
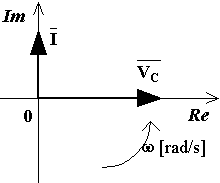
La figura riportata sopra mostra le varie grandezze sinusoidali prese fino ad ora in considerazione rappresentate sul piano di Gauss.

Fonte: http://www.itiscopernicofe.it/itis/didattic/matdid/3H/3%5EH-Elettrotecnica.doc

Grandezze alternate sinusoidali