Densità
Densità
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Densità
DENSITA’
INTRODUZIONE
In fisica alcune grandezze servono a descrivere le caratteristiche dei corpi esaminati. Chi ha massa maggiore, 1 dm3 di paglia o 1 dm3 di piombo? Le due dimensioni volumiche sono identiche, ma le masse? Per esperienza diremo che ha massa maggiore 1 dm3 di piombo. Ma su cosa si fonda questa nostra certezza?
Rispondiamo alla domanda capovolgendo il problema. Chi occupa il volume maggiore tra 1 kg di piombo e 1 kg di paglia? E qui si capisce che il volume della paglia deve essere maggiore del volume del piombo, e non di poco. Rispondiamo per esperienza solo perché abbiamo comunque una chiara idea dei due corpi.
E se i due corpi da confrontare fossero meno noti della paglia e del piombo? Immaginiamo di porci la stessa domanda considerando due liquidi come ad esempio la benzina e il diesel. Qui l’esperienza aiuterebbe solo i più esperti, ma per rispondere alla domanda dobbiamo introdurre il concetto di densità.
Da ciò che abbiamo appena osservato è evidente che sostanze diverse presentano una diversa capacità di addensare la materia. Se però ci limitassimo alle semplici osservazioni cadremmo nello stesso errore degli scienziati prima di Galileo: ci baseremmo soltanto su ciò che vediamo ma così facendo la nostra ricerca finirebbe per aggirarsi vanamente per un oscuro laberinto. Perciò seguiremo l’esempio di Galileo: non ci baseremo solo sulle semplici osservazioni ma analizzeremo il problema con misure, tabelle, grafici e calcoli ben precisi.
PRIMA ANALISI
Non si può mai iniziare un’analisi fisica vera e propria senza avere a disposizione delle misure. Nella figura accanto abbiamo due dadi di stesso lato di 10cm. Essi hanno perciò entrambi lo stesso volume: 1.000cm3 = 1dm3. Il primo è di Legno, il secondo di Ferro. Se li pesiamo, però, vediamo che il primo possiede una massa di 0,62 kg mentre il secondo ha una massa di ben 7,8kg: questo perché i due cubi sono composti da sostanze diverse. E’ evidente che la materia nel Ferro è più addensata che nel legno: infatti, dentro 1dm3 di Ferro vi stanno 7,8 kg di massa mentre dentro lo stesso volume vi entrano solo 0,62 kg di legno. Comunemente diciamo che il Legno è più leggero del Ferro: più propriamente dovremmo affermare che il Ferro è in grado di concentrare nello stesso volume più materia del legno.
Adesso ci poniamo di risolvere il problema di trovare una grandezza fisica che descriva la capacità di una sostanza di concentrare la materia. Per farlo useremo la matematica. Consideriamo il Legno ed il Ferro e facciamo una Tabella Massa-Volume. Partiamo dal ferro. Poiché un cubetto di volume 1dm3 di Ferro possiede 7,8kg di materia, due cubetti avranno un volume complessivo di 2dm3 ed una massa complessiva di 7,8kg X 2 = 15,6kg; 3 volume possiederanno un volume complessivo di 3dm3 ed una massa di 7,8kg X 3 = 23,4kg, ecc…
Finisci tu la Tabella!
Tabella 1: Massa e Volume per Ferro e Legno
FERRO |
LEGNO |
||
MASSA (kg) |
VOLUME (dm3) |
MASSA (kg) |
VOLUME (dm3) |
7,8 |
1 |
0,62 |
1 |
15,6 |
2 |
1,24 |
2 |
23,4 |
3 |
? |
3 |
46,8 |
6 |
3,72 |
? |
78 |
? |
? |
10 |
? |
20 |
12,4 |
? |
Cosa puoi vedere dalla Tabella? Pensaci un po’ Il…………………… rimane costante! In altre parole, se divido la Massa per il Volume di una stessa sostanza il valore che ottengo non cambia mai, qualunque sia la Massa o il Volume usato. Per il Ferro il rapporto Massa/Volume vale 7,8 kg/dm3 ; per il Legno 0,62 kg/dm3. Questo rapporto è chiamato universalmente massa volumica o molto più comunemente densità e viene solitamente indicato con il simbolo d, r (rho) o δ (delta). Noi utilizzeremo quest’ultimo simbolo e scriveremo:
δ = Massa/Volume (1)
Posso perciò dare una prima definizione di densità:
la densità è il rapporto fra la Massa e il Volume di una sostanza (definizione matematica)
Per misurare la densità di un corpo possiamo misurarne la massa con una bilancia. Per misurare il volume possiamo invece usare dell'acqua e un cilindro graduato come abbiamo visto nella sezione in Laboratorio. Dal momento che nel Sistema Internazionale la massa si misura in kilogrammi (kg) e il volume in m3 avremo che l'unità di misura della densità assoluta d nel Sistema Internazionale è il kg/m3, anche se spesso si usa la densità in kg/dm3, kg/litro, g/cm3 e g/litro. In generale la densità dei solidi è maggiore della densità dei liquidi che a sua volta è maggiore della densità dei gas, ma esiste un'importante eccezione, l'acqua: il ghiaccio (solido) galleggia sull'acqua (liquida) perché la sua densità è minore di quella dell'acqua.
Bene. Adesso che sappiamo cosa è la densità dobbiamo studiarne le proprietà.
GRANDEZZE INTENSIVE ED ESTENSIVE
Da ciò che abbiamo osservato, la proprietà che caratterizza la densità è che essa non dipende dalla Massa o dal Volume di un oggetto ma solo dal tipo di sostanza che lo compone. In altre parole: ogni sostanza possiede la sua propria densità. Vediamo perché.
Dimostriamo che 100kg di Ferro possiedono la stessa densità di 100g di Ferro. Se ho tante palline di Ferro da 100g l’una, per ottenere 100kg devo metterne insieme 1.000; così facendo la Massa aumenta di 1.000 volte ma anche il Volume aumenta di 1.000 volte e la densità, che è definita dalla frazione Massa/Volume, non cambia perché ho moltiplicato per 1.000 sia il numeratore (Massa) sia il denominatore (Volume).
Una grandezza che non dipende dalla quantità di materia si dice intensiva, all’opposto di quelle che dipendono dalla quantità di materia che si chiamano estensive. In altre parole, le grandezze intensive sono quelle che assumono sempre lo stesso valore indipendentemente da quanta materia sto considerando; all’opposto, le grandezze estensive sono quelle il cui valore cambia quando cambia la massa. La densità è sicuramente intensiva perché non dipende dalla massa, come abbiamo appena osservato sopra. Per chiarirti le idee, nomina qualche grandezza estensiva ed almeno un’altra grandezza intensiva che tu conosci già.
Poiché è intensiva, la densità dipende solo da cosa compone un oggetto e per questo è molto importante. Infatti, la densità è considerata a tutti gli effetti la “carta di identità” del corpo in esame. Ogni corpo ha una propria densità che lo distingue e, tramite essa, si può risalire alla sua composizione chimico-fisica.
PROPORZIONALITA’ DIRETTA FRA MASSA E VOLUME
Adesso diamo una seconda occhiata alla Tabella. Cosa notiamo? Fissata la sostanza (Ferro o Legno), Massa e Volume sono ……………………………………….. fra loro! Dalle Scuole Medie sapete che due grandezze sono tra loro direttamente proporzionali quando “all’aumentare dell’una aumenta anche l’altra con la stessa proporzione” . Ed infatti se osservate la Tabella, una volta che è fissata la sostanza, se raddoppia la massa raddoppia anche il volume, se triplica la massa triplica anche il volume … e viceversa.
Le grandezze direttamente proporzionali godono di una importantissima proprietà: “se due grandezze sono direttamente proporzionali, esse hanno sempre rapporto costante e viceversa” . Ma allora il fatto che il rapporto Massa/Volume –cioè la densità- di una sostanza rimanga costante qualunque sia il Volume o la Massa è una diretta conseguenza del fatto che Massa e Volume sono direttamente proporzionali!
Il rapporto fra due grandezze direttamente proporzionali si chiama costante di proporzionalità diretta. Ma il rapporto fra Massa e Volume è proprio la densità! Da ciò segue subito una seconda definizione:
la densità è la costante di proporzionalità diretta fra Massa e Volume di una sostanza (def. geometrica)
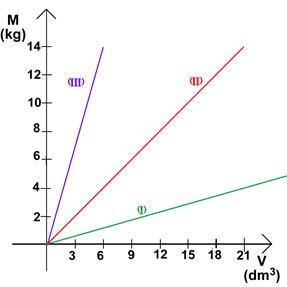
Figura 1: Grafico Massa-Volume per 3 sostanze differenti
 ANALISI GRAFICA
ANALISI GRAFICA
Se alle medie avete fatto dei grafici, dovreste già conoscere qual è il grafico di due grandezze direttamente proporzionali. Disegnate voi il grafico della Tabella 1, con la Massa sull’asse Y ed il Volume sull’asse X! Cosa viene fuori?
Adesso guardate la figura accanto: esso mostra i grafici Massa-Volume di tre sostanze diverse.
Voglio conoscere la densità delle tre sostanze: come posso fare? Pensaci un po’…
Adesso che hai calcolato le tre densità confronta le tre rette: cosa noti?
Rifletti per un attimo su come hai ottenuti i valori della densità: hai segnato un punto sulla retta leggendo i suoi valori di Massa e di Volume, cioè i valori Y ed X del punto, dopodiché li hai divisi fra loro. Puoi perciò scrivere:
δ = Y/X (2)
Il rapporto “Y/X” di una qualsiasi retta passante per l’origine si chiama pendenza della retta. Perciò possiamo dare una terza definizione di densità:
la densità è la pendenza della retta del grafico Massa-Volume di una sostanza (def. grafica)
ANALISI FISICA
Torniamo alla Tabella 1. Abbiamo detto che il Ferro ed il Legno hanno una densità ben precisa (δFerro=7,8 kg/dm3 ; δLegno=0,62 kg/dm3): ma questi valori corrispondono proprio a quello della Massa quando il Volume è 1dm3! E’ un caso? Pensaci….
Ecco allora la quarta ed ultima definizione di densità, quella più fisica in quanto lega direttamente questa grandezza al concetto di concentrazione di materia da cui siamo partiti:
la densità rappresenta la massa contenuta in un’unità di volume (definizione fisica)
Dunque, a parità di Volume il Legno ha una Massa minore del Ferro perché la sua densità è minore e dunque dentro lo stesso Volume di 1dm3 è in grado di contenere meno materia.
Riassumiamo tutte e quattro le definizioni con un unico esempio. Un geologo afferma che:”il marmo possiede una densità di 2,7kg/dm3”. Ciò significa che:
- Il rapporto fra la Massa ed il Volume di un qualsiasi frammento di marmo, grande o piccino che sia, è sempre 2,7kg/dm3
- La Massa ed il Volume del Marmo sono direttamente proporzionali e la loro costante di proporzionalità è 2,7kg/dm3
- Il grafico Massa-Volume del Marmo è una retta passante per l’origine la cui pendenza - cioè il rapporto Y/X – è sempre 2,7kg/dm3
- Un dm3 di marmo possiede sempre una massa di 2,7kg
Fonte: http://www.liceoagnoletti.it/attivita/attivita_professori/fisicafacile/Documenti/IB_IF_DENSITA.doc
Autore del testo: non indicato nel documento di origine
Parola chiave google : Densità tipo file : doc
Densità
Visita la nostra pagina principale
Densità
Termini d' uso e privacy