Dinamica relativistica

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Dinamica relativistica

DINAMICA RELATIVISTICA

Quando le velocità in gioco dei corpi è sensibilmente inferiore alla velocità della luce le leggi fondamentali della dinamica e le leggi di conservazione della quantità di moto e dell’energia sono quelle definite dalla fisica classica.

Se, invece, le velocità sono prossime a c, come per esempio negli acceleratori di particelle e nei raggi cosmici, tali leggi cambiano. In particolare la quantità di moto totale di un sistema definita come prodotto di massa e velocità, 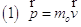non si conserva in tutti i sistemi di riferimento inerziali, cioè nei sistemi che si muovono di MRU l’uno rispetto all’altro. In tal caso la legge di conservazione vale solo se la quantità di moto classica viene sostituta con quella relativistica definita nel seguente modo:

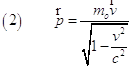
Oss 1. La quantità di moto classica e relativistica differiscono per il fattore 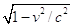, lo stesso termine che è presente nelle equazioni per la dilatazione

temporale e per la contrazione delle lunghezze che, essendo minore di uno rende la quantità di moto relativistica sempre maggiore di quella classica.

Oss 2. La grandezza m₀ è la massa a riposo del corpo, ovvero la massa misurata in un sistema in cui il corpo è in quiete. Tale massa nella formulazione classica (1) fornisce anche la misura dell’inerzia del corpo, cioè la sua tendenza a mantenere la velocità che possiede. Invece nella relazione relativistica (2) si deve fare ben distinzione tra massa e inerzia. Infatti, mentre la massa a riposo di un corpo è un invariante, cioè non cambia a seconda del sistema di riferimento che la misura, la sua inerzia dipende dal sistema di riferimento in cui è misurata. E’ possibile così definire la massa inerziale relativistica:

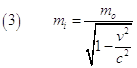
E’ importante evidenziare che una tale dipendenza della massa inerziale dalla velocità non significa che il corpo in moto diviene più grande, nel senso di essere più ricco di materia. La (3) stabilisce invece che quanto maggiore è la velocità del corpo rispetto a un dato osservatore, tanto più difficile è modificare il suo stato di moto applicando una medesima forza.

Einstein dimostrò che la massa inerziale fornisce più informazione rispetto alla massa invariante 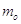di un corpo, perché stabilisce anche il contenuto di energia di un corpo rispetto al mondo esterno. In particolare per un corpo in movimento a velocità v, la sua energia totale E è data:

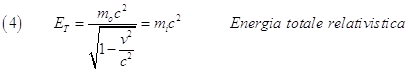
Oss1. Questa relazione, stabilendo un’equivalenza tra massa ed energia, dice quanta energia può essere estratta da un corpo di data massa e viceversa quanta massa è equivalente a una data quantità di energia. Quindi a creare la massa (inerziale) di un corpo non v’è solo la sostanza che posso pesare di cui questo è composto ma anche qualunque forma di energia. Un corpo caldo per esempio ha una massa maggiore di uno freddo perché ha un’energia termica più grande; analogamente un corpo ruotante su se stesso ha una massa maggiore di uno non ruotante perché il primo ha più energia rotazionale.

Oss2. L’espressione (4) mostra che mentre nella fisica classica un corpo fermo lontano da campi di forze (gravitazionale, elettrico, magnetico) non ha energia, nella fisica relativistica il corpo in quiete possiede un’energia intrinseca cioè a riposo diversa da zero espressa dalla relazione:

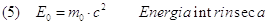
Oss3. Il “tasso di cambio” tra energia e massa è particolarmente favorevole per la massa per la presenza del termine c². Questo “vantaggio” è sfruttato nei reattori nucleari i quali sono una sorta di “forno” in cui l’energia viene generata tramite una reazione di fissione a catena controllata. Ad esempio, una delle possibile reazioni che si possono verificare durante la fissione dell’isotopo dell’uranio U-235 è:

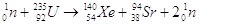
Avviene che la somma delle masse dei prodotti della reazione è minore della somma delle masse

dei reagenti. Questa perdita di massa si trasforma, per la (5), in energia. Nelle stelle l’enorme quantità di energia da esse liberata è dovuta alla fusione di due protoni e di due neutroni, provenienti da atomi di idrogeno, per formare un nucleo di elio liberando un’energia:

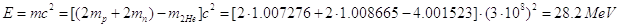
E’ un’energia molto elevata tenendo conto che si tratta di un singolo processo. Si ricordi, a titolo di esempio, che l’energia di legame delle molecole d’acqua è di circa 6 eV. Da ciò si deduce che l’energia che si libera durante i processi nucleari è milioni di volte superiore a quella che si può ottenere dai processi chimici a parità di materiale coinvolto!

Oss4. Se un corpo quando è in movimento ha un’energia totale data dalla (4) mentre quando è fermo la sua energia è fornita dalla (5) è evidente che la sua energia cinetica relativistica vale:

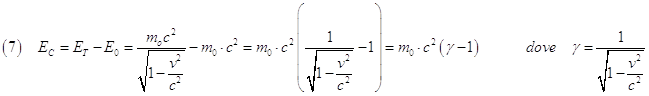
Oss5. In un sistema isolato non si conserva in generale l’energia cinetica né l’energia a riposo ma l’energia totale (4) definita anche come:

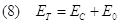
RELAZIONE TRA ENERGIA E QUANTITA’ DI MOTO (*)

Dimostriamo ora la seguente relazione fra l’energia totale, la quantità di moto e l’energia a riposo:

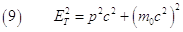
Al secondo membro della (9) sostituiamo p con la sua espressione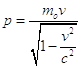

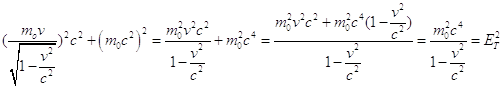
Oss1. L’equazione (9) è utile perché permette di calcolare rapidamente la quantità di moto se è nota l’energia totale o viceversa. In particolare, se voglio determinare l’energia totale:

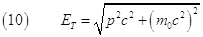
Oss 2. La (9) non è limitata soltanto per corpi o particelle dotati di massa ma anche per le particelle avente massa a riposo nulla cioè per i fotoni, i costituenti delle onde elettromagnetiche, come la luce. Per le onde elettromagnetiche, essendo m₀=0, la (9) si riduce alla seguente:

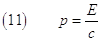
Quindi, un fascio di luce o di ogni altro tipo di onde elettromagnetiche, pur non avendo massa, trasportando energia possiede quantità di moto.

Che un'onda elettromagnetica trasporti energia è evidente per tutti. Infatti, è proprio attraverso i suoi raggi luminosi che il Sole ci riscalda e permette la vita sulla terra. Ma cosa vuol dire che l'onda trasporta quantità di moto? Vuol dire che, se un'onda elettromagnetica incide su una parete e viene da essa assorbita, non solo la parete si scalda ( l'energia dell'onda viene assorbita) ma essa

acquista anche una quantità di moto. Poiché una variazione della quantità di moto è associata a un impulso 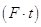, si può capire come un fascio di luce investendo un corpo, possa sviluppare su di esso una forza per un certo tempo ed una pressione.

Questa proprietà della luce è alla base del cosiddetto “effetto fotoelettrico” di fondamentale importanza in molte applicazioni tecnologiche, basti ricordare i pannelli fotovoltaici.

Alle onde elettromagnetiche possiamo quindi associare grandezze tipiche ondulatorie come la frequenza e la lunghezza d'onda e grandezze tipiche dei corpuscoli come l'energia e la quantità di moto.

(*) formule utili che legano v-Ec e v-p: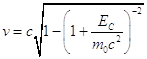

Fonte: http://www.fisicaweb.org/doc/relativita/DINAMICA%20RELATIVISTICA.doc

Sito web :http://www.fisicaweb.org

Autore del testo: non indicato nel documento di origine

Parola chiave google : Dinamica relativistica tipo file : doc

Dinamica relativistica