Viscosità
Viscosità appunti
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Viscosità
Quando un blocco scivola su un pavimento ruvido, risente di una forza di attrito che si oppone al moto. Analogamente, un fluido che scorre su una superficie ferma risente di una forza che si oppone al moto. La caratteristica di opporsi al moto viene chiamata viscosità del fluido. Fluidi come l’ aria hanno bassa viscosità, fluidi più densi come l’acqua hanno viscosità maggiore e fluidi come il miele o la melassa sono caratterizzati dalla loro alta viscosità.
Per entrare più in dettaglio, consideriamo una situazione di grande importanza pratica: lo scorrere di un fluido in un condotto. Esempi di sistemi di questo tipo sono l’acqua che scorre in un tubo metallico e il sangue che scorre in un’arteria o in una vena.
Se il fluido fosse ideale, cioè con viscosità zero scorrerebbe nel tubo con una velocità di modulo uguale in tutto il fluido, come indicato nella figura A.
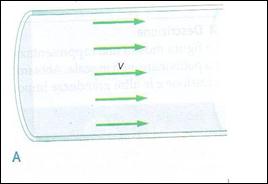
I fluidi reali, con viscosità diversa da zero, scorrono in modo simile a quello mostrato nella figura B.
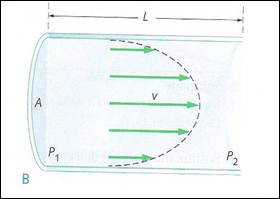
In questo caso, il fluido è in quiete vicino alle pareti del tubo e scorre con la sua massima velocità nel centro del tubo. Poiché porzioni adiacenti del fluido scorrono le une sulle altre con velocità di modulo diverso, dobbiamo esercitare una forza sul fluido per mantenere il flusso, proprio come dobbiamo esercitare una forza per far scivolare un blocco su una superficie ruvida.
La forza che causa lo scorrimento di un fluido è fornita dalla differenza tra le pressioni P1- P 2, in una data lunghezza L del tubo.
Sperimentalmente vediamo che la differenza di pressione richiesta per mantenere il fluido in movimento è proporzionale alla lunghezza del tubo e al modulo della velocità media v del fluido.
Per esempio, la viscosità dell’acqua a temperatura ambiente è 0,00101N· s/m2 e la viscosità del sangue a 37°C è 0,0027N· s/m2. Nella tabella sottostante sono riportate alcune viscosità.
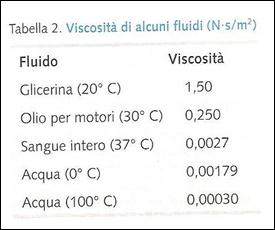
Un modo conveniente di caratterizzare il flusso di un fluido è in funzione del volume di fluido che passa per un dato punto in un determinato intervallo di tempo. Sappiamo inoltre che il volume che passa attraverso una sezione in un determinato intervallo di tempo è semplicemente vA, la portata, dove V è il modulo della velocità media del fluido e A è l’area della sezione del tubo attraverso la quale scorre il fluido. Ricavando dall’equazione P1- P 2 = 8ph è il modulo della velocità media, otteniamo v = (P1- P 2)A/8phL.
Autrice: Surace Maria Pia
Fonte: estratto da http://www.francescozumbo.it/zumbo/lavori-studenti/2008/cd-5g-2007-2008/lavori/maria-pia-surace-5g-2007-2008.doc
Sito web da visitare: http://www.francescozumbo.it/
Parola chiave google : Viscosità tipo file : doc
Visita la nostra pagina principale
Viscosità
Termini d' uso e privacy