Fisica appunti
Fisica appunti
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

PROGETTO DI FISICA DI MARIA PIA SURACE
In fisica, quando parliamo di fluidi, ci riferiamo a sostanze che possono scorrere rapidamente da un punto all’altro e che non hanno una forma propria, ma assumono quella del recipiente che le contiene. Quando utilizziamo il termine fluidi, solitamente, ci riferiamo sia a liquidi sia a gas. E’ difficile pensare a qualcosa di più importante dei fluidi per la nostra vita quotidiana. Infatti, iniziamo la nostra vita come una cellula piena di fluidi e sospesa in un fluido. Viviamo immersi in un fluido che respiriamo. I fluidi che percorrono il nostro sistema circolatorio sono la ninfa della nostra esistenza. Se non fosse per i gas presenti nella nostra atmosfera e per l’acqua sulla superficie della terra, noi non potremmo esistere.
Perciò, per la notevole importanza che assumono in natura, i fluidi forniscono un’ottima opportunità per applicare le conoscenze di fisica.
![]()
![]()
Le proprietà fisiche usate per descrivere gli oggetti solidi (massa, volume ecc..) spesso non sono sufficienti o sono comunque scomode per descrivere i fluidi, per i quali occorre introdurre grandezze opportune. Una caratteristica molto utile per descrivere un fluido è la sua densità, p, definita come il rapporto fra la massa, M , e il volume, V.
M
V
 p =
p =
Più denso è un materiale, più massa ha in un determinato volume. E’ opportuno notare che la densità è la stessa, qualunque sia la quantità di massa totale del sistema.
Per esempio per riempire un recipiente cubico con il lato di un metro, occorre una tonnellata di acqua. Quindi l’acqua ha la seguente densità:
paq = densità dell’acqua =1000kg/m3
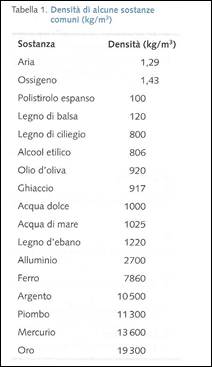
L’elio che riempie un pallone aerostatico, per esempio,ha una densità di appena 0,179 kg/m3 e la densità dell’aria nella nostra stanza è circa 1,29 kg/m3. nella parte alta della scala della densità c’è l’oro, che allo stato solido ha una densità di 19300 kg/m3
Ulteriori esempi di densità di materiali comuni sono riportati nella tabella sottostante:
![]()
Un’altra caratteristica dei fluidi, come sappiamo, è la pressione, P.
La pressione, P, è una misura della forza per unità di area:
P = F/A
La pressione aumenta se aumenta la forza esercitata su una data area o se una data forza viene applicata su un’area minore. Per esempio, se premiamo con un dito su un palloncino (come mostrato nella foto), non otteniamo grandi effetti e notiamo solo una piccola deformazione. Se invece premiamo con uno spillo con la stessa forza, facciamo scoppiare il pallone. La differenza sta nel fatto che la stessa forza, applicata a un’area più piccola, causa una pressione abbastanza grande da rompere il pallone.

Pressione atmosferica
Siamo tutti abituati a vivere e lavorare sotto pressione, circa 1kg-peso per cm2. Questa è la pressione atmosferica, Pat, diretta conseguenza del peso dell’aria sopra di noi.
In unità SI, la pressione atmosferica ha il seguente valore:
Pat = 1,01 · 105 N/ m2
Viene introdotta per la pressione la nuova unità di misura specifica, il pascal (Pa):
1 Pa = 1 N/m2
Questa unità di misura deve il suo nome allo scienziato francese Blaise Pascal (1623-1662), pioniere negli studi sui fluidi. Perciò la pressione atmosferica può essere scritta come:
Pat = 101 kPa

L’aria intorno a noi esercita una forza di circa 1 kg p su ogni cm2 del nostro corpo. Poiché questa
forza è uguale in tutte le direzioni ed è contrastata da un’uguale pressione all’interno del nostro corpo, generalmente non ci accorgiamo che esiste. Tuttavia, se si pompa l’aria fuori da un reci-
piente sigillato (a sinistra), la pressione atmosferica produce una forza non bilanciata verso l’in-
terno. Il collasso del recipiente che ne risulta, illustra in modo evidente la pressione che ci circon-
da. Una stecca pneumatica (a destra) utilizza lo stesso principio della pressione non bilanciata.
Una manica di plastica viene posta intorno all’arto offeso e gonfiata a una pressione maggiore di quella atmosferica e quindi della pressione interna del corpo. L’aumento della pressione esterna
rallenta l’emorragia e tende anche a immobilizzare l’arto nel caso possa essere fratturato. ( le stecche pneumatiche vengono adoperate dagli escursionisti o da altre persone che possono trovarsi
nella necessità di un trattamento di emergenza lontano da un presidio medico. Prima di essere gon-
fiata, la stecca pneumatica ha le dimensioni e il peso di una carta di credito).
In meterologia viene spesso ancora utilizzata, per la pressione atmosferica, un’altra unità, il bar, definito come:
1bar =105 Pa = 1Pat
Pressione relativa
In molti casi siamo interessati alla differenza tra una data pressione e quella atmosferica. Per esempio, un pneumatico sgonfio al suo interno non ha una pressione zero, ma uguale a quella atmosferica. Per gonfiare lo pneumatico a 241 kPa, la sua pressione interna deve essere maggiore di quella atmosferica di questa quantità: perciò, P = 241kPa + Pat = 342 kPa.
Per trattare situazioni del genere, introduciamo la pressione relativa, Pr, definita come:
Pr = P - Pat
Perciò è la pressione relativa che viene determinata attraverso un manometro per la pressione degli pneumatici. Quindi, dobbiamo ricordare che la pressione reale in questi casi è maggiore di una quantità Pat.

La pressione è uguale in tutte le direzioni
Per spiegare questa ulteriore caratteristica della pressione utilizziamo l’esempio riportato qui sotto:
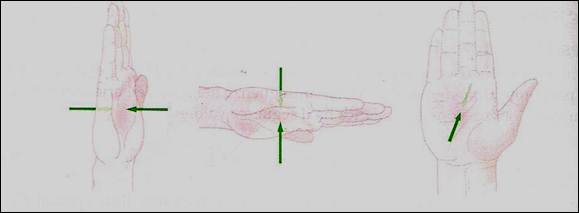
La figura illustra le forze esercitate sulla mano dalla pressione atmosferica. Se la mano è verticale,
la pressione atmosferica spinge verso destra e verso sinistra in modo uguale, cosicché la mano non risente di alcuna forza risultanti. Se essa è posta orizzontalmente, la pressione atmosferica esercita sulla mano forze verso l’alto e verso il basso che hanno essenzialmente la stessa intensità, dando di nuovo una risultante nulla. Questa eliminazione delle forze esiste indipendentemente dall’orientazione della mano.
Perciò possiamo concludere che:
La pressione in un fluido agisce in modo uguale in tutte le direzioni ed è sempre perpendicolare alla superficie sulla quale si esercita.
Nei fluidi la pressione è strettamente legata alla profondità. Infatti se prendiamo in considerazione, per esempio, un sottomarino da guerra possiamo notare come l’aumento di pressione sia dovuto all’aumento della quantità di acqua che pesa sul sottomarino a mano a mano che scende in profondità.
Per comprendere meglio come funziona questo fenomeno, consideriamo un contenitore cilindrico riempito fino a un’altezza h con un fluido di densità p, come nella figura sottostante. La superficie superiore del fluido è aperta all’atmosfera, con una pressione Pat. Se l’area di questa superficie è A, la forza esercitata dall’atmosfera sulla superficie superiore del fluido è:
Fsup = Pat · A
Sul fondo del contenitore, la forza verso il basso è data dalla Fsup più il peso del fluido.
Ricordando che il peso, che indichiamo con la lettera W per distinguerlo dalla nostra pressione, è uguale al prodotto della massa m per l’accelerazione gravitazionale g,e a sua volta la massa è uguale al prodotto della densità p per il volume v possiamo scrivere così:
W = m · g = p · v · g = p (h · A) g
Quindi abbiamo:
Finf = Fsup + W = Pat · A + p ( h· A)g
Infine, otteniamo la pressione sul fondo dividendo Finf per l’area A:

Pat· A + p (h· A)g
A

Finf
A
Perciò a mano a mano che scendiamo a una profondità h in un fluido di densità p, la pressione cresce di:
p · g ·h
Naturalmente, questa relazione non vale solo per il fondo del recipiente, ma per qualsiasi punto a profondità h al di sotto della superficie. Perciò se la profondità cresce di h, la pressione aumenta di pgh. A una profondità h, quindi, la pressione P è data da:
P = Pat + pgh
Questa espressione vale per qualsiasi liquido con densità costante p la cui superficie è alla pressione atmosferica Pat.
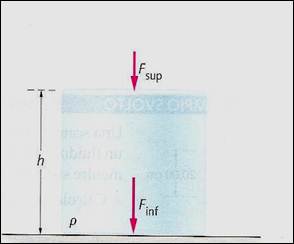
Pressione e peso di un fluido: la forza che spinge Variazione della pressione con la profon-
verso il basso, sul fondo del recipiente, è maggiore dità: se il punto 2 è maggiore del punto 1 di
di quella che spinge verso l’alto, sulla superficie h, la sua pressione è maggiore di una quan-
superiore del fluido. La differenza è data dal peso tità pgh.
del fluido contenuto nel recipiente.

Un importante strumento basato sulla variazione di pressione legata alla profondità è il barometro, che può essere utilizzato per misurare la pressione atmosferica. Il più semplice tipo di barometro fu costruito per la prima volta da Evangelista Torricelli nel 1643. per fabbricare questo barometro dobbiamo riempire un lungo cilindro di vetro con un liquido di densità p. Poi lo capovolgiamo e lo immergiamo nello stesso tipo di liquido contenuto in una vaschetta, come mostrato nella figura sottostante. Una parte del fluido contenuto nel cilindro fluirà nella vaschetta, lasciando uno spazio vuoto nella parte superiore. Né rimarrà, tuttavia, abbastanza da creare una differenza di livello h tra il liquido nella vaschetta e quello nel cilindro.
L’idea fondamentale del barometro è quella che questa differenza di altezza è direttamente correlata alla pressione atmosferica che spinge sulla superficie del liquido nella vaschetta. Per comprendere come ciò avvenga, osserviamo innanzitutto che la pressione nella parte vuota, in alto, del cilindro è zero. Quindi, la pressione a una profondità h al di sotto del vuoto è 0 + pgh = pgh. Al livello del liquido nella vaschetta sappiamo che la pressione è una atmosfera, Pat . Pertanto, segue che:
Pat = pgh
Se queste pressioni non fossero uguali, ci sarebbe una differenza di pressione tra il liquido nel cilindro è quello nella vaschetta, quindi una forza risultante e un fluire del liquido. Perciò una misura di h ci fornisce immediatamente la pressione atmosferica.
Un fluido che viene spesso utilizzato in questo tipo di barometro è il mercurio (Hg), che ha una densità p = 1,3595 · 104 kg /m3. la corrispondente altezza della colonna di mercurio è:
Pat
pg
1,013 · 105 Pa
(1,3595 · 104 kg / m3) (9,81 m /s2 )
 h = = = = 760 mm
h = = = = 760 mm
In effetti, la pressione atmosferica è definita in termini di millimetri di mercurio (mmHg):
1 atmosfera = Pat = 760 mmHg


Un'altra caratteristica dei fluidi è senz’altro quella che essi tendono a livellarsi se la pressione sulla loro superficie è la stessa in ogni punto della superficie stessa.
Prendiamo in considerazione per esempio un tubo a U ( come mostrato nella figura sottostante), contenente una certa quantità di liquido di densità p. Il liquido raggiunge lo stesso livello su entrambi i rami del tubo, che sono aperti all’atmosfera. Pertanto, la pressione alla base di ogni ramo è la stessa: Pat + pgh. Quindi il fluido che si trova nella sezione orizzontale del tubo viene spinto con uguale forza dai due lati e di conseguenza rimane fermo.

Quando i livelli sono uguali, la pressione alla
base di ciascun ramo di un tubo a U è la stessa.
Di conseguenza il fluido nella sezione è in
equilibrio.
In quest’altra figura invece i due rami del tubo a U sono riempiti a livelli differenti. Pertanto la pressione alla base dei due rami è diversa, con una pressione alla base dei due rami è diversa, con una pressione maggiore alla base del ramo di destra. Il fluido che si trova nella sezione orizzontale, allora, sentirà una forza risultante verso sinistra che lo farà muovere in quella direzione riequilibrando i livelli del liquido nei due rami.
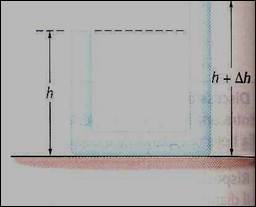
Con altezze diverse, le pressioni sono differenti.
In questo caso, la pressione è maggiore alla base
del ramo di destra, quindi il liquido fluisce verso
sinistra e i livelli si riequilibrano.
Possiamo arrivare alla stessa conclusione considerando la situazione di minima energia. Consideriamo un tubo a U che sia inizialmente riempito allo stesso livello in entrambi i rami. Ora trasportiamo, sollevandola, una piccola quantità di fluido da un ramo all’altro, creando così un dislivello. Questa operazione provoca un aumento dell’energia potenziale della quantità di fluido, perché l’unica cosa che è variata nel sistema è la sua posizione. Perciò, concludiamo che il sistema ha un minimo di energia quando i livelli del liquido sono uguali e una maggiore energia quando sono diversi. Se due liquidi differenti con diverse densità vengono messi nello stesso tubo a U, i livelli nei due rami non sono uguali. Però la pressione alla base di ciascun ramo deve essere uguale come nel caso di un singolo fluido.
. 

Sappiamo che se la superficie di un fluido di densità p è esposta all’atmosfera con una pressione.
Pat, la pressione a una profondità h al di sotto della superficie è:
P = Pat + pgh
Supponiamo ora che la pressione atmosferica venga aumentata da Pat a Pat + DP.
Di conseguenza , la pressione alla profondità h sarà:
P = Pat + DP + pgh = ( Pat + pgh ) + DP
Perciò, incrementando la pressione alla superficie del fluido di una quantità DP, abbiamo aumentato della stessa quantità la pressione in ogni punto del fluido.
Questo è il principio di Pascal:
Una pressione esterna applicata a un fluido racchiuso in un recipiente viene trasmessa inalterata in ogni punto del fluido.
Un classico esempio di applicazione del principio di Pascal è l’ elevatore(o torchio) idraulico, mostrato schematicamente nella figura sottostante. È formato da due cilindri, uno di area di base
A1, l’altro di area di base A1 > A2. I cilindri, contenenti ciascuno un pistone, sono collegati attraverso un tubo e riempiti con un fluido.
Inizialmente i pistoni sono allo stesso livello ed esposti all’atmosfera.
Supponiamo di premere su un pistone 1 con una forza F1 verso il basso. Ciò provoca un aumento di pressione della quantità:
DP = F1 / A1
Per il principio di Pascal, la pressione nel cilindro 2 aumenta della stessa quantità.
Pertanto, sul pistone 2 abbiamo un aumento della forza verso l’alto dovuto al fluido pari a:
F2 = (DP) A2
Sostituendo DP = F1 / A1, troviamo:
A2
A1
 F2 = ( F1 / A1 ) A2 = F1 > F1
F2 = ( F1 / A1 ) A2 = F1 > F1
Più precisamente, supponiamo che A2 sia 100A1. Quindi, premendo verso il basso sul pistone 1 con una forza F1, spingiamo verso l’alto sul pistone 2 con una forza F2 = 100F1, cioè la nostra forza è stata moltiplicata per 100.
Proprio come una leva, c’è una compensazione tra lo spostamento che deve fare la forza F1 e l’ aumento ottenuto. Questo fatto viene illustrato nella figura sottostante, dove mostriamo il pistone 1 che viene spinto verso il basso di un tratto d1. Ciò fa spostare un volume di fluido uguale a A1d1. Lo stesso volume di liquido fluisce nel cilindro 2, dove causa l’ innalzamento del pistone 2 di un tratto d2. Uguagliando i due volumi, abbiamo:
A1d1 = A2d2
Oppure:

A1
A2
Perciò, nell’esempio appena dato, se muoviamo il pistone 1 giù di un tratto d1, il pistone 2 sale di un tratto d2 = d1/100. la nostra forza sul pistone 1 è stata moltiplicata per 100, ma la distanza percorsa dal pistone è stata divisa per 100.
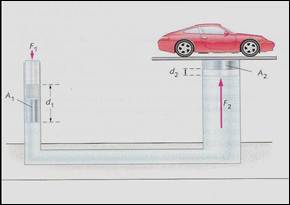
ELEVATORE IDRAULICO
Una forza F1 applicata sul pistone piccolo causa una forza molto più grande F2 che agisce sul pistone 2.
![]()
Il fatto che la pressione aumenti con la profondità porta a molte conseguenze importanti. Una di queste è che un fluido esercita una spinta verso l’alto su qualsiasi oggetto vi sia immerso. Questa forza viene chiamata forza di galleggiamento o forza di Archimede.
Per comprendere l’origine del galleggiamento, consideriamo un blocco di forma cubica immerso in un fluido di densità p, come nella figura sottostante.
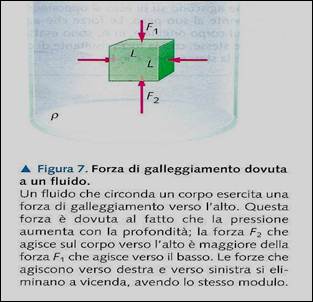
Il fluido circostante esercita forze normali su ognuna delle facce. Chiaramente, le forze orizzontali che spingono verso destra e verso sinistra sono uguali e quindi si eliminano a vicenda, non avendo nessun effetto sul blocco.
La situazione, tuttavia, è piuttosto differente per le forze verticali. Osserviamo, per esempio, che la forza verso il basso esercitata sulla faccia superiore è minore di quella verso l’alto esercitata sulla faccia inferiore, poiché la pressione sulla faccia più bassa è maggiore. Questa differenza tra le forze dà luogo a una forza risultante verso l’alto, la forza di galleggiamento.
Calcoliamo questa forza.
Innanzitutto, assumiamo che il lato del blocco abbia lunghezza L e che la pressione sulla superficie superiore sia P1. La forza verso il basso quindi è:
F1 = P1A = P1L2
Ricordiamo che l’area di un quadrato di lato L è L2 . Poi consideriamo la faccia inferiore. La pressione su questa faccia è data dall’equazione P2 = P1 + pgh, con una differenza di profondità
h = L:
P2 = P1 + pgL
Pertanto, la forza verso l’alto esercitata sulla faccia inferiore del cubo è:
F2 = P2A = ( P1+ pgL ) L2 = P1L2 + pgL3 = F1 + pgL3
Se fissiamo la direzione positive verso l’alto, la forza verticale risultante esercitata dal fluido sul blocco è:
F tot = F2 – F1 = pgL3
Come avevamo previsto, il blocco risente di una forza risultante verso l’alto.
Il valore esatto della forza di galleggiamento è di una certa importanza, come vedremo. Ricordando che il volume del cubo è L3 , ne segue che pgL3 è il peso del fluido che occuperebbe lo stesso volume del cubo. Pertanto, la forza di galleggiamento è uguale al peso del fluido spostato per far posto al cubo. Questo è un caso particolare del principio di Archimede:
Un corpo completamente immerso in un fluido sente una spinta di
galleggiamento verso l’alto di intensità uguale al peso del fluido
spostato.
Più in generale se una parte di volume V di un corpo viene immersa in un fluido di densità p, la forza di galleggiamento può essere espressa come:
Fg = pgV
Il volume V può essere il volume totale del corpo oppure anche una sua frazione.
Per vedere che il principio di Archimede è del tutto generale, consideriamo l’oggetto immerso mostrato nella figura A. Se rimpiazzassimo questo oggetto con un equivalente volume di fluido, come risulta nella figura B, nel recipiente non ci sarebbe altro che fluido in equilibrio
statico.
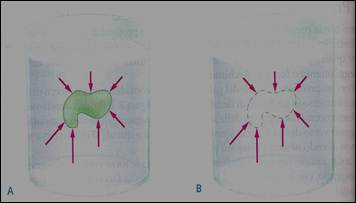
Di conseguenza, concludiamo che la forza risultante su questo«oggetto fluido» deve essere verso l’alto e di intensità uguale al suo peso. E’ qui l’idea chiave di questo problema: poiché il corpo originale e l’«oggetto fluido» occupano la stessa posizione, le forze che agiscono sulle loro superfici sono identiche e quindi la forza risultante è la stessa per i due corpi.
Pertanto, il corpo originale sente una spinta verso l’alto uguale al peso del liquido che ha spostato, che è uguale al peso dell’«oggetto fluido».
Il galleggiamento
Quando un oggetto galleggia, la spinta di Archimede è uguale al suo peso. Supponiamo di immergere lentamente un blocco di legno in un recipiente d’acqua. All’inizio solo una piccola quantità d’acqua viene spostata e la spinta di Archimede è una frazione del peso del blocco. Se lasciassimo il blocco in questo momento, esso si immergerebbe ulteriormente nell’acqua. Mentre continuiamo a immergere il blocco , una maggior quantità d’acqua viene spostata, facendo aumentare la spinta di Archimede
.

Infine, raggiungiamo la situazione della figura 9B, nella quale il blocco inizia a galleggiare. In questo caso la spinta di Archimede uguaglia il peso del legno. Questo significa che il peso dell’acqua spostata è uguale al peso del blocco di legno.
Quindi:
Un corpo galleggia se sposta una quantità di fluido pari al suo peso.
Ciò è illustrato nella figura 10A, nella quale mostriamo il volume d’acqua che ha il peso uguale al peso del blocco di legno. Analogamente, nella figura 10B mostriamo la quantità d’acqua necessaria per avere lo stesso peso di un blocco di metallo. Chiaramente, se il metallo viene completamente immerso, la spinta di Archimede è solo una frazione del suo peso e quindi affonda. Se invece, il metallo ha la forma di una scodella, come nella figura 10C, può spostare un volume d’acqua che abbia il suo peso e quindi galleggiare.

Un altro modo per cambiare il galleggiamento di un corpo è quello di alterare la sua densità.
![]()
Supponiamo di voler innaffiare il cortile, ma di non avere un ugello nebulizzatore alla fine del tubo. Senza nebulizzatore l’acqua esce dal tubo piuttosto lentamente e raggiunge il terreno a una distanza di non oltre mezzo metro. Se però mettiamo un dito alla fine del tubo, chiudendo l’apertura fino a farla diventare molto piccola, l’acqua spruzza con una velocità più alta e va molto più lontano. Perché diminuire l’apertura produce questo effetto?
Per rispondere a questa domanda, iniziamo considerando un semplice sistema che si comporta allo stesso modo. Immaginiamo che un fluido scorra con velocità v1 all’interno di un condotto cilindrico con una sezione di area A1,come nella parte sinistra della figura sottostante. Se il condotto si restringe a una sezione di area A2 come nella parte destra della figura, il fluido scorrerà con una nuova velocità v2 .
Possiamo trovare la velocità nella sezione più stretta del condotto supponendo che la quantità dei fluido che passa per il punto 1 in un dato tempo Dt debba anche passare per il punto 2 nello stesso tempo. Se non fosse così, il sistema acquisterebbe o perderebbe una certa quantità di fluido. Per trovare la massa di liquido che passa dal punto1 nel tempo Dt , osserviamo che il fluido in questo tempo percorre una distanza v1Dt. Di conseguenza il volume del fluido che passa dal punto1è:
DV1 = A1 v1Dt
Quindi, la massa di fluido che passa dal punto1 è:
Dm1 = p1DV1 = p1 A1 v1Dt
Analogamente, la massa che passa dal punto2 nel tempo Dt è:
Dm2 = p2DV2 = p2 A2 v2Dt
Osserviamo che il fluido può avere densità diverse nei punti1 e 2.
Infine, uguagliando queste due masse otteniamo la relazione tra v1 e v2 :
Dm1 = Dm2
p1 A1 v1Dt = p2 A2 v2Dt
Semplificando Dt troviamo:
p1A1 v1 = p2 A2 v2
Questa equazione viene chiamata equazione di continuità
Possiamo comprimere facilmente la maggior parte dei gas, e questo significa che la loro densità può variare. La maggior parte dei liquidi, invece è praticamente incomprimibile, perciò la loro densità rimane essenzialmente costante. Salvo diverso avviso, assumeremo che tutti i liquidi che tratteremo in questo testo siano perfettamente incomprimibili. Perciò, per i liquidi, p1 e p2 sono uguali e l’ equazione di continuità si riduce alla seguente:
A1 v1 = A2 v2

In questo paragrafo applicheremo il teorema dell’ energia cinetica ai fluidi, stabilita una relazione tra la pressione di un fluido, il modulo della sua velocità e l’altezza alla quale si trova. Questa relazione è nota come equazione di Bernoulli.
![]()
Iniziamo considerando un sistema nel quale varia il modulo della velocità come quello mostrato nella figura sottostante.
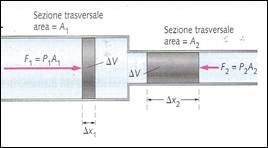
Abbiamo già mostrato che il modulo della velocità del fluido aumenta nel passaggio dalla zona 1 alla 2; indagheremo ora sulla corrispondente variazione nella pressione.
Calcoleremo prima il lavoro totale eseguito sul fluido mentre si muove da una da un’ altra zona all’ altra. Questo risultato dipenderà dalla pressione nel fluido. Una volta ottenuto il lavoro totale, il teorema dell’ energia cinetica ci permetterà di uguagliarlo alla variazione dell’ energia cinetica del fluido. Tutto ciò ci fornirà la relazione desiderata tra la pressione e i modulo della velocità.
Consideriamo una quantità di fluido di lunghezza Dx1, che viene spinta nella direzione del moto dalla pressione P1. Perciò la pressione esegue un lavoro positivo, DW1, su tale quantità. Osservando che la forza esercitata è F1 = P1DA1 e che il lavoro è dato dal prodotto di questa forza per lo spostamento, il lavoro sul fatto sulla quantità è:
P1= F1Dx1 = =A1Dx1
Il volume dell’elemento di fluido è DV1 = A1Dx1, così il lavoro fatto da P è:
DW1 = P1 DV1
Ora, quando il fluido arriva nella zona 2,ridente di una forza in direzione opposta al suo moto dovuta alla pressione P2. Perciò P2 esegue un lavoro negativo sulla quantità di fluido. Seguendo lo stesso procedimento di prima, possiamo scrivere il lavoro fatto da P2 come:
DW2 = - P2DV2
Per un fluido incomprimibile, il volume della quantità non cambia nel passare dalla zona 1 alla 2. Pertanto:
DV1 = DV2 = DV
Utilizzando questo risultato, possiamo scrivere il lavoro totale fatto sulla quantità di fluido come segue:
DWtotale = DW1 + DW2 = P1DV - P2DV = (P1 - P2 ) DV
Il passo finale è quello di uguagliare il lavoro totale alla variazione dell’energia cinetica:
DWtotale = (P1 - P2 ) DV = Kfinale - Kiniziale = K2- K1 1
Troviamo l’energia cinetica della quantità di fluido, sapendo che la sua massa è:
1
Dm = pDV
Perciò la sua energia cinetica è:
1
2
1
2
 K = (Dm)v2 = ( pDV) v2
K = (Dm)v2 = ( pDV) v2
Utilizzando questa espressione nell’equazione 1, abbiamo:
1
2
1
2
 DWtotale = (P1 - P2 ) DV = ( pv12 – pv22) DV
DWtotale = (P1 - P2 ) DV = ( pv12 – pv22) DV
1
2
1
2
 P1 + pv12 = P2+ pv22
P1 + pv12 = P2+ pv22
1
2
 L’equazione 2 equivale a dire che P + pv2 è costante. Perciò c’è una specie di equilibrio tra la
L’equazione 2 equivale a dire che P + pv2 è costante. Perciò c’è una specie di equilibrio tra la pressione in un fluido e il modulo della sua velocità: se la velocità aumenta, la pressione diminuisce.
![]()
Se il fluido scorre attraverso il condotto mostrato nella figura sottostante, la sua altezza aumenta da y1 a y2 nel passare da una regione all’altra. Poiché l’area del condotto è costante, tuttavia, la velocità non cambia. Perciò la variazione dell’energia cinetica dell’elemento di fluido mostrato nella figura è nulla.
Il lavoro totale fatto sulla quantità di fluido è la somma di quello fatto dalla pressione in ciascuna delle due zone più quello fatto dalla gravità. Il lavoro fatto dalla pressione è, perciò:
DWpressione = DW1 + DW2 = ( P1 - P 2 ) DV
Mentre la quantità di fluido sale, la gravità compie su di essa un lavoro negativo. Ricordando che la massa della quantità è:
Dm = pDV
Il lavoro fatto della gravità è:
DWgravità = - Dm (y1- y2) = pDVg (y1- y2)
Ponendo il lavoro totale uguale a zero ( essendo Dk = 0), otteniamo:
DWtotale = DWpressione + DWgravità = ( P1 - P 2 ) DV - pg(y1- y2) DV = 0
Semplificando DV e riordinando come prima, otteniamo:
P1 + pg y1 = P2+ pg y2
In questo caso è P + pg y che è costante, quindi la pressione diminuisce se aumenta l’altezza.

![]()
Consideriamo un recipiente d’acqua mostrato nella figura sottostante. Se viene praticato un foro nella superficie laterale del recipiente a una profondità h al di sotto della superficie, qual è il modulo della velocità dell’acqua che esce dal foro?
1
2
 P1 + pv12 + pg y1 = Pat + 0 + pgh
P1 + pv12 + pg y1 = Pat + 0 + pgh
Per il punto 2 abbiamo che l’altezza è y2 = 0, per la scelta fatta dell’origine e la velocità di uscita dal foro v2 è l’incognita. La pressione P2 è la pressione atmosfera, perché il foro mette in comunicazione l’acqua con l’atmosfera. Perciò, per il punto 2 si ha:
1
![]() 2
2
1
2
 P2 + ppv22+ pg y2 = Pat + pv22 + 0
P2 + ppv22+ pg y2 = Pat + pv22 + 0
Uguagliando le espressioni trovate, otteniamo:
1
![]() 2
2
1
![]() 2
2
 P1 + pv12 + pg y1 = P2 + pv22+ pg y2
P1 + pv12 + pg y1 = P2 + pv22+ pg y2
 Pat + pgh = Pat + 1 pv22
Pat + pgh = Pat + 1 pv22
![]()
Risalendo rispetto a v2 troviamo:
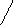 v2 = 2gh
v2 = 2gh
Questo risultato è noto come la legge di Torricelli.
L’espressione trovata per v2 è la velocità di un corpo che cade in caduta libera da un’altezza h. in altre parole, l’acqua emerge dal foro con una velocità che ha lo stesso modulo che avrebbe se fosse caduta dalla superficie. Analogamente, se il flusso d’acqua che emerge dal foro fosse diretto verso l’alto avrebbe esattamente una velocità di modulo tale da farla salire ad una altezza h, proprio fino alla superficie libera dell’acqua.

![]()
Finora abbiamo considerato soltanto liquidi «ideali». In particolare, abbiamo supposto che i liquidi scorressero senza perdite dovute all’ attrito e che le molecole del liquido non interagissero l’una con l’altra. In questo paragrafo considereremo le conseguenze che si hanno quando queste supposizioni non valgono più.
![]()
Quando un blocco scivola su un pavimento ruvido, risente di una forza di attrito che si oppone al moto. Analogamente, un fluido che scorre su una superficie ferma risente di una forza che si oppone al moto. La caratteristica di opporsi al moto viene chiamata viscosità del fluido. Fluidi come l’ aria hanno bassa viscosità, fluidi più densi come l’acqua hanno viscosità maggiore e fluidi come il miele o la melassa sono caratterizzati dalla loro alta viscosità.
Per entrare più in dettaglio, consideriamo una situazione di grande importanza pratica: lo scorrere di un fluido in un condotto. Esempi di sistemi di questo tipo sono l’acqua che scorre in un tubo metallico e il sangue che scorre in un’arteria o in una vena.
Se il fluido fosse ideale, cioè con viscosità zero scorrerebbe nel tubo con una velocità di modulo uguale in tutto il fluido, come indicato nella figura A.
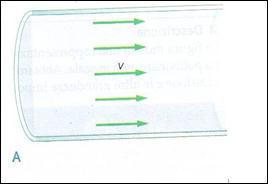
I fluidi reali, con viscosità diversa da zero, scorrono in modo simile a quello mostrato nella figura B.
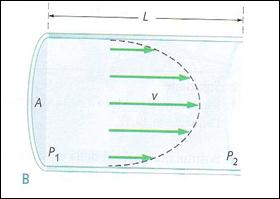
In questo caso, il fluido è in quiete vicino alle pareti del tubo e scorre con la sua massima velocità nel centro del tubo. Poiché porzioni adiacenti del fluido scorrono le une sulle altre con velocità di modulo diverso, dobbiamo esercitare una forza sul fluido per mantenere il flusso, proprio come dobbiamo esercitare una forza per far scivolare un blocco su una superficie ruvida.
La forza che causa lo scorrimento di un fluido è fornita dalla differenza tra le pressioni P1- P 2, in una data lunghezza L del tubo.
Sperimentalmente vediamo che la differenza di pressione richiesta per mantenere il fluido in movimento è proporzionale alla lunghezza del tubo e al modulo della velocità media v del fluido.
Inoltre, è inversamente proporzionale alla sezione A del tubo. Combinando queste osservazioni, possiamo scrivere la differenza di pressione nella seguente formula:
vL
A
 P1- P 2 a
P1- P 2 a
La costante di proporzionalità tra la differenza di pressione e vL/A è legata al coefficiente di viscosità, h, di un fluido. Infatti, la viscosità è definita in modo che la differenza di pressione sia data dalla seguente espressione:
vL
A
 P1- P 2 = 8ph
P1- P 2 = 8ph
Da questa equazione possiamo vedere che le dimensioni del coefficiente di viscosità sono N· s/m2.
Un’unità comunemente utilizzata negli studi sui fluidi viscosi è il poise, in onore del fisiologo francese Jean Léonard Marie Poiseuille (1799-1869), definito come:
1poise = 1dyn· s/cm2
Per esempio, la viscosità dell’acqua a temperatura ambiente è 0,00101N· s/m2 e la viscosità del sangue a 37°C è 0,0027N· s/m2. Nella tabella sottostante sono riportate alcune viscosità.
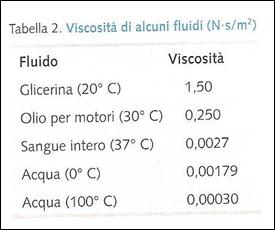
 Un modo conveniente di caratterizzare il flusso di un fluido è in funzione del volume di fluido che passa per un dato punto in un determinato intervallo di tempo. Sappiamo inoltre che il volume che passa attraverso una sezione in un determinato intervallo di tempo è semplicemente vA, la portata, dove V è il modulo della velocità media del fluido e A è l’area della sezione del tubo attraverso la quale scorre il fluido. Ricavando dall’equazione P1- P 2 = 8ph è il modulo della velocità media, otteniamo v = (P1- P 2)A/8phL. Moltiplicando questa espressione per l’area del tubo si ha:
Un modo conveniente di caratterizzare il flusso di un fluido è in funzione del volume di fluido che passa per un dato punto in un determinato intervallo di tempo. Sappiamo inoltre che il volume che passa attraverso una sezione in un determinato intervallo di tempo è semplicemente vA, la portata, dove V è il modulo della velocità media del fluido e A è l’area della sezione del tubo attraverso la quale scorre il fluido. Ricavando dall’equazione P1- P 2 = 8ph è il modulo della velocità media, otteniamo v = (P1- P 2)A/8phL. Moltiplicando questa espressione per l’area del tubo si ha:
DV
Dt
(P1- P 2) A2
8ph
 modulo della velocità del flusso = = vA =
modulo della velocità del flusso = = vA =
utilizzando il fatto che l’area della sezione del tubo è A = pr4, dove r è il suo raggio, otteniamo il risultato conosciuto come equazione di Poiseuille:
(P1- P 2) pr4
8ph
DV
DV
 =
=
Osserviamo che la portata varia con la quarta potenza del raggio del tubo, perciò una piccola variazione del raggio corrisponde a una grande variazione della portata.
![]()
La superficie dell’acqua e degli altri fluidi si comporta per molti aspetti come se fosse una membrana elastica. Questo effetto è conosciuto come tensione superficiale.
Per comprendere l’origine della tensione superficiale, iniziamo osservando che le molecole di un fluido esercitano forze attrattive le une sulle altre. Perciò una molecola che si trova all’interno del fluido risente di forze in tutte le direzioni dovute alle molecole che la circondano da tutti i lati , come indicato nella figura sottostante. La forza risultante su tale molecola è zero. Se una molecola si avvicina alla superficie, tuttavia, risente di una forza risultante che tende ad allontanarla dalla superficie poiché non ci sono molecole di fluido dall’altra parte per attrarre la molecola in quella direzione. Ne segue che deve essere effettuato del lavoro per spostare una molecola dall’interno di un fluido verso la superficie e che l’energia del fluido aumenta per ogni molecola spostata in tale direzione.
Poiché occorre dell’energia per aumentare la superficie di un liquido, la situazione è simile all’energia richiesta per allungare una molla o un filo di gomma. Perciò la superficie di un liquido si comporta come se fosse elastica, resistendo alla tendenza ad aumentare la sua area.

Fonte: http://www.francescozumbo.it/zumbo/lavori-studenti/2008/cd-5g-2007-2008/lavori/maria-pia-surace-5g-2007-2008.doc
Autore: MARIA PIA SURACE
APPUNTI DI FISICA
APPUNTI SINTETICI PER IL RECUPERO
Premessa
Questi appunti sintetici non contengono figure, dimostrazioni ed esempi, pertanto non sostituiscono né il libro di testo né gli appunti delle spiegazioni in classe.
Essi sono una esemplificazione dei concetti minimi di sufficienza ed uno strumento di recupero per una didattica breve.
LA FISICA
La FISICA è la scienza che studia i fenomeni che avvengono in natura senza trasformazione di materia.
METODO SPERIMENTALE
Il metodo sperimentale è il metodo di indagine scientifica per studiare i fenomeni naturali.
Esso si basa sulla sperimentazione e sull’elaborazione dei dati misurati. Le fasi sono:
Si osserva un fenomeno, si raccolgono dei dati, si formula un’ipotesi , si esegue una sperimentazione in laboratorio. Se i risultati della sperimentazione confermano l’ipotesi fatta, questa si assume come legge del fenomeno.
Una legge è la descrizione di come avviene un fenomeno. Essa si considera vera fino a quando qualcuno ne dimostra il contrario.
GRANDEZZE, MISURA E MISURAZIONE
Tutti i corpi hanno delle proprietà, alcune delle quali si possono misurare e si dicono proprietà oggettive, esse esprimono una quantità , per esempio il peso, il volume ecc.
Altre proprietà di un corpo non sono misurabili e sono soggettive, esse esprimono una qualità, per esempio la bellezza, la simpatia, l’estetica, ecc.
La Fisica si occupa delle proprietà oggettive che si chiamano grandezze.
Una grandezza è qualunque proprietà della materia che si può misurare.
Misurare significa confrontare una grandezza con un’altra presa come riferimento.
L’unità di misura è una grandezza che viene presa come riferimento per misurare altre grandezza della stessa natura.
La misura è il valore di una grandezza che si legge nella misurazione
La misura si esprime mediante un numero seguito dall’unità di misura.
2,7 m 15 kg 23 s
Essa esprime quante volte l’unità di misura è più grande della grandezza da misurare.
ERRORI DI MISURAZIONE
Quando si eseguono le misurazioni si commettono degli errori che ci impediscono di conoscere il valore vero di una misura.
Quando si usa uno strumento la misura che si ottiene ha un errore detto errore di sensibilità.
L’errore di sensibilità è dato dalla variazione minima di una grandezza che lo strumento riesce a misurare. L’errore di sensibilità è uguale al valore che si legge sulla scala dello strumento tra due suddivisioni successive (in una squadra da disegno generalmente è 1mm=0,1cm).
Un modo per ridurre gli errori consiste nell’effettuare un numero di misurazioni e poi si calcola la media aritmetica delle misure ottenute.
Per calcolare il valore medio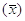 si sommano tutte le misure effettuate (x1, x2,…xn) ed il risultato si divide per il loro numero (n):
si sommano tutte le misure effettuate (x1, x2,…xn) ed il risultato si divide per il loro numero (n):
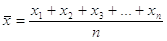
E’ possibile determinare anche il valore dell’ incertezza assoluta (ia o Ea); il metodo più semplice consiste nel calcolare la semidispersione massima (d): si sottrae al valore massimo delle misure il valore minimo, la differenza si divide per due:
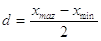
L’incertezza relativa (ir o Er) si calcola dividendo l’incertezza assoluta con il valore medio:
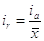
L’incertezza relativa si esprime spesso in percentuale, che si ottiene moltiplicando l’incertezza relativa per 100.
Il valore medio rappresenta il valore più probabile della misura,
L’incertezza assoluta esprime il valore dell’errore commesso nelle misurazioni.
L’errore relativo ci dà indicazione sulla precisione della misura.
Ottenuto il valore medio e l’incertezza assoluta si può scrivere l’intervallo di indeterminazione
(o di incertezza).
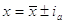
valore vero = valore medio 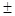 incertezza assoluta
incertezza assoluta
L’intervallo di indeterminazione indica un insieme di valori tra cui molto probabilmente è compreso il valore vero.
Quindi per esprimere la misura di una lunghezza che è stata misurata ottenendo il valore 12,5cm usando un righello con la suddivisione in mm (ossia con un errore di sensibilità di 1mm=0,1cm) si scrive:
L = ( 12,5 ± 0,1 ) cm
L è il simbolo della grandezza: la lunghezza
12,5 è la misura che è stata letta
± è il simbolo dell’intervallo di indeterminazione
0,1 è l’incertezza della misura
cm è l’unità di misura
Una misura si dice diretta se viene letta direttamente sullo strumento di misura.
Una misura è indiretta se si ottiene da calcoli eseguiti con altre grandezze
(Esempio l’area di un rettangolo = base x altezza)
SISTEMA DI MISURA INTERNAZIONALE
Per uniformare nel mondo le unità di misura, gli scienziati si sono riuniti e di comune accordo hanno definito le unità di misura valide per tutti, ottenendo il Sistema Internazionale (SI)
Un sistema di misura è un insieme di unità di misura usato per misurare le grandezze, alcune delle quali sono fondamentali e tutte le altre sono derivate.
Una grandezza si dice fondamentale se la sua unità di misura è stata scelta arbitrariamente.
Le grandezze derivate sono quelle le cui unità di misura derivano dalle grandezze fondamentali.
Due grandezze sono omogenee se sono della stessa natura e possono essere misurate con la stessa unità di misura (esempio: l’altezza, la profondità ,l’altitudine, lo spessore sono delle lunghezze)
Il sistema internazionale è l’insieme delle unità di misura riconosciute a livello internazionale.
Le grandezze fondamentali del sistema internazionali sono sette:
Grandezza Unità di misura
Lunghezza l metro m
Massa m chilogrammo kg
Tempo t secondo s
Temperatura T kelvin K
Intensità luminosa I candela cd
Intensità di corrente elettrica i ampere A
Quantità di sostanza grammo-molecola (mole) mol
Occorre fare attenzione a distinguere la massa dal peso.
La massa si può definire, in modo pratico, come la quantità di materia contenuta in un corpo.
Il peso, detto anche forza peso, è la forza con cui un corpo è attratto dalla Terra.
Nello spazio, lontano dai pianeti, la massa non varia mentre il peso è nullo.
Relazioni tra grandezze
Due grandezze sono direttamente proporzionali se al raddoppiare di una raddoppia anche l’altra,oppure al dimezzare di una dimezza anche l’altra.
Esempio: l’importo da pagare è direttamente proporzionale al numero di matite acquistate.
In fisica: l’allungamento di una molla è direttamente proporzionale alla forza applicata.
In formula: il rapporto tra le grandezze è costante : Y : X = K
Due grandezza sono inversamente proporzionali se al raddoppiare di una l’altra dimezza.
Esempio: nella divisione di un pacchetto di caramelle, il numero di caramelle che spetta a ciascuno è inversamente proporzionale al numero dei ragazzi.
In fisica: il volume di una siringa contenente aria è inversamente proporzionale alla forza applicata sul pistone della siringa.
In formula: il prodotto tra le grandezze è costante : Y x X = K
FORZE E LORO MISURAZIONE
In natura troviamo vari tipi di forze:
- elastica:
- di gravità
- elettrica
- magnetica
- muscolare
- ecc.
Alcune forze agiscono per contatto, ossia è necessario il contatto tra i corpi per poter applicare la forza, altre hanno un’azione a distanza, cioè si esercitano anche quando i corpi sono a distanza (esempio: forza di gravità, forza magnetica tra due calamite ecc.)
La forza è una grandezza fisica capace di:
- deformare un corpo ( esempio una molla che si allunga a causa di una forza)
- modificare il moto di una corpo ( es. un calcio ad un pallone)
- mantenere in equilibrio un corpo (la reazione dei un chiodo a cui è appeso un quadro)
La forza nel Sistema Internazionale si misura in Newton (N).
Altra unità di misura usata praticamente è il chilogrammo-forza (kgf)
1 kgf = 9,81 N (a volte si approssima: 1 kgf ≈ 10N)
LEGGE DEGLI ALLUNGAMENTI ELASTICI o legge di Hooke
Se una molla (corpo elastico) si tira con una forza essa si allunga (deforma).
Se si raddoppia la forza applicata, si nota che la deformazione raddoppia, quindi possiamo affermare:
(legge di Hooke) La deformazione di un corpo elastico è direttamente proporzionale alla forza applicata e il loro rapporto è costante.
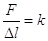
che si può anche scrivere come:
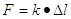
dove: F= forza; k= costante elastica; Δl = (variazione di lunghezza) deformazione
Sotto l’azione delle forze i corpi si deformano elasticamente se il valore della forza agente è inferiore al valore della resistenza del materiale.
Se si supera il valore di resistenza il corpo o si spezza (rottura fragile) o si deforma in modo permanente (plasticizzazione).
Il comportamento elastico si ha quando annullando la forza il corpo ritorna nella forma iniziale.
Il comportamento plastico si ha quando il corpo resta deformato dopo aver tolto la forza agente.
GRANDEZZE SCALARI E VETTORIALI
Le grandezze scalari, sono quelle grandezze che si possono definire con la sola misura.
( Esempi: massa, tempo, temperatura, lunghezza, volume, superficie ecc..).
Le operazioni con le grandezze scalari si eseguono mediante l’algebra numerica.
Le grandezze vettoriali sono quelle che per definirle completamente occorre precisare:
l’intensità o modulo, la direzione, il verso e il punto di applicazione.
(Esempi: forza, spostamento, velocità, momento ecc..).
Per rappresentare le grandezze vettoriali si usano i VETTORI, che sono dei segmenti orientati.

Per sapere se una grandezza è vettoriale bisogna considerare se ha senso rispondere alle domande:
- In che direzione agisce la grandezza? In che verso?
Se ha senso rispondere alle domande la grandezza è vettoriale, altrimenti è scalare.
La retta di azione di un vettore è la retta alla quale esso (segmento orientato) appartiene.
Il vettore risultante è un vettore che da solo ha gli stessi effetti di un sistema (insieme) di vettori. Il vettore risultante è la somma dei vettori dati.
Il vettore equilibrante è un vettore che da solo annulla l’effetto di un insieme di vettori.
Il vettore equilibrante è opposto al vettore risultante.
Somma tra due vettori (regola del parallelogramma):
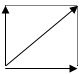
MOMENTO E COPPIA DI FORZE
Il momento di una forza rispetto ad un punto di rotazione è una grandezza vettoriale che ha il modulo pari al prodotto del modulo della forza per il braccio della forza.
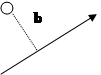
M = F • b
F
Il braccio di una forza rispetto ad un punto di rotazione è la minima distanza tra il punto e la retta di azione della forza. La distanza si deve misurare sulla retta perpendicolare con la retta di azione della forza passante per il punto di rotazione.
Il momento quindi è una grandezza che misura l’effetto rotazionale di una forza.
Il momento, nel Sistema Internazionale, si misura in newton per metro (Nm); un’altra unità di misura è il chilogrammo-forza per metro (kgfm).
Una coppia di forze sono due forze parallele e discordi aventi lo stesso modulo.
Il momento di una coppia di forze è costante rispetto a qualunque punto di rotazione che si consideri.
Esso è dato dal prodotto del modulo di una delle forze (F) per la distanza (d) delle loro rette di azione.
M =F • d
EQUILIBRIO DEI CORPI
MODELLI: CORPO RIGIDO, PUNTO MATERIALE
Nello studio dei fenomeni fisici la scienza si serve dei modelli.
Un modello è la semplificazione di un fenomeno reale. Le semplificazioni introdotte servono a facilitare lo studio dei fenomeni naturali.
Per esempio, nello studio del movimento dei corpi si considera un modello in cui i corpi si muovono senza attriti.
Due modelli sono: il corpo rigido e il punto materiale
Un corpo si considera rigido se sotto l’azione di forze non si deforma e non si rompe. Naturalmente il corpo rigido è un modello astratto, perché i corpi reali si deformano e si rompono.
Un corpo reale si può considerare rigido se le deformazioni che subisce sono trascurabili rispetto alle sue dimensioni.
Un altro modello è il punto materiale.
Il punto materiale è un corpo avente massa ma privo di volume.
Un corpo può essere considerato un punto materiale se le sue dimensioni sono trascurabili rispetto alle distanze considerate nel fenomeno. (Esempio: l’automobile che percorre l’autostrada)
I VINCOLI
Un vincolo è qualunque causa che limita il movimento di un corpo.
Il vincolo per avere la sua funzione deve essere in grado di annullare l’effetto delle forze applicate al corpo. La forza con cui reagisce il vincolo è detta reazione vincolare.
I vincoli ideali sono in grado di reagire a qualunque forza; i vincoli reali hanno un limite di resistenza.
BARICENTRO
Il baricentro di un corpo è il punto di applicazione della forza peso del corpo. La forza peso di un corpo è la risultante di tutte le forze peso delle piccole particelle di cui è costituito il corpo.
Il centro di massa è il punto in cui si può pensare concentrata la massa del corpo quando esso viene considerato come punto materiale.
Per i corpi non molto estesi il baricentro coincide con il centro di massa.
EQUILIBRIO DEL CORPO RIGIDO
Un corpo rigido è in equilibrio se:
- la somma vettoriale di tutte le forze applicate al corpo è nulla : F tot = 0
- la somma vettoriale di tutti i momenti delle forze applicate al corpo è nulla: M tot = 0
MACCHINE SEMPLICI
Una macchina semplice è un dispositivo che permette di equilibrare due forze, una detta forza motrice (Fm),o potenza, e l’altra detta forza resistente (Fr), o resistenza.
Una macchina è vantaggiosa se la forza motrice è maggiore della forza resistente: Fm > Fr.
Una macchina è svantaggiosa se la forza motrice è minore della forza resistente: Fm< Fr
Una macchina è indifferente se la forza motrice è uguale alla forza resistente: Fm = Fr
Il vantaggio si calcola dividendo la forza resistente con la forza motrice: 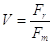
LE LEVE
Una leva è un corpo (asta rigida) girevole intorno ad un punto detto fulcro.
La leva è di primo genere se il fulcro è posto tra la forza motrice e la forza resistente.

Fm
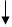
Fr
La leva di primo genere può essere:
- Vantaggiosa: se il fulcro è posto più vicino alla forza resistente;
- Svantaggiosa: se il fulcro è posto più vicino alla forza motrice;
- Indifferente: se il fulcro è posto nel mezzo tra la forza motrice e la forza resistente.
Fr
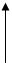 La leva è di secondo genere se il fulcro è posto ad un estremo e la forza resistente è posta tra il fulcro e la forza motrice.
La leva è di secondo genere se il fulcro è posto ad un estremo e la forza resistente è posta tra il fulcro e la forza motrice.

Fm

La leva di secondo genere è sempre vantaggiosa; al limite è indifferente se la forza motrice e resistente sono applicate nello stesso punto.
La leva è di terzo genere se il fulcro è posto ad un estremo e la forza motrice è posta tra il fulcro e la forza resistente.
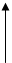
Fm

La leva di terzo genere è sempre svantaggiosa; al limite è indifferente se la forza motrice e la forza resistente sono applicate nello stesso punto.
Una leva è in equilibrio se il momento della forza motrice è uguale al momento della forza resistente, applicando questa uguaglianza si risolvono i problemi sulle leve:
Mm =Mr
Fm • bm = Fr • br
CARRUCOLA FISSA
La carrucola fissa è una ruota che gira attorno ad un asse, disposto normalmente e al centro della ruota, sostenuta da una staffa fissata ad un vincolo.
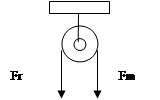
La carrucola serve a variare la direzione di una forza, mentre il modulo della forza non viene modificato.
La carrucola fissa, è una macchina indifferente poiché la forza motrice è uguale alla forza resistente:
Fm = Fr
La carrucola fissa equivale ad una leva di primo genere indifferente (i due bracci sono uguali).
CARRUCOLA MOBILE
La carrucola mobile è una carrucola che scorre lungo una corda con un capo fissato ad un vincolo.
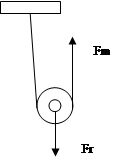
La forza resistente (Fr) è applicata nella staffa attaccata all’asse della carrucola, mentre la forza motrice è applicata al capo libero della fune.
E’ una macchina vantaggiosa poiché la forza motrice è uguale alla metà della forza resistente:
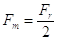
Quindi il vantaggio (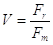 ) per la carrucola mobile è uguale a 2.
) per la carrucola mobile è uguale a 2.
La carrucola mobile equivale ad una leva di secondo genere che ha la forza resistente posta nel punto di mezzo tra il fulcro e la forza motrice.
STATI DELLA MATERIA
In natura i corpi si posso presentare in tre stati:
- solido: i solidi hanno forma e volume propri;
- liquido: i liquidi hanno volume proprio e la forma del recipiente che li contiene;
- aeriforme: gli aeriformi non hanno né forma e né volumi propri e sono comprimibili.
I liquidi e gli aeriformi sono detti anche fluidi perché hanno la proprietà di poter “fluire” attraverso un foro o un tubo
DENSITÀ E PESO SPECIFICO
La densità è il rapporto tra la massa di un corpo ed il volume che la massa occupa.
Densità = massa : volume ρ = m : V
L’unità di misura nel S.I. è kg/m3
Il peso specifico è il rapporto tra il peso di un corpo ed il suo volume
Peso specifico = peso : volume γ = Fp : V
L’unità di misura nel S.I. è N/m3 ma si misura anche in kgf/m3
Il peso specifico si calcola anche con la densità:
Peso specifico = densità x accelerazione di gravità
γ = ρ x g
dove g = 9,81 m/s²
IDROSTATICA
L’idrostatica è il capitolo della fisica che studia l’equilibrio dei corpi fluidi (liquidi ed aeriformi)
LA PRESSIONE
La pressione è data dal rapporto tra il modulo della forza agente perpendicolarmente su una superficie e l’area della superficie stessa.
Pressione = forza perpendicolare : area della superficie 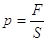
Dove (p) è la pressione, (F) è la forza ed(S) è l’area.
La pressione, nel Sistema Internazionale, si misura in pascal (Pa): 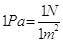
Altra unità di misura, non del S.I., è l’atmosfera (atm): 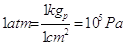
LEGGE DI PASCAL
La pressione esercitata su una qualunque superficie di massa fluida si trasmette in tutti i punti, in tutte le direzioni e con lo stesso valore.
LEGGE DI STEVINO
La pressione idrostatica è direttamente proporzionale all’altezza (h) della colonna di fluido sovrastante e alla densità (ρ) del fluido stesso.
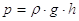
La pressione idrostatica è la pressione dovuta al peso proprio del fluido.
Per la legge di Stevino la pressione ad una data profondità dipende solo dalla densità e dalla profondità dal livello del liquido e non dipende dalla forma del recipiente.
PRINCIPIO DI ARCHIMEDE
Un corpo immerso in un liquido è soggetto a una forza diretta dal basso verso l’alto (verticalmente), il cui modulo è uguale al peso del liquido spostato.
Sa = ρl x g x Vci
Dove DF è la spinta di Archimede, (ρl) è la densità del liquido, g è l’accelerazione di gravità (=9,81m/s²) e (Vci) è il volume del corpo immerso.
Un corpo galleggia se la spinta di Archimede è maggiore della forza peso del corpo, altrimenti affonda. Ossia galleggia se la densità del corpo è inferiore a quella del liquido, altrimenti affonda.
CINEMATICA
La CINEMATICA è il capitolo della fisica che studia il moto dei corpi da un punto di vista qualitativo.
ELEMENTI DEL MOTO
Gli elementi necessari per poter descivere un moto sono tre:
1) SISTEMA DI RIFERIMENTO
2) TRAIETTORIA
3) LEGGE ORARIA
Il sistema di riferimento è un punto, o un insieme di punti, rispetto al quale si misurano le posizioni degli altri oggetti.
Normalmente, si assume come sistema di riferimento un sistema di assi cartesiani x, y, z.
Un corpo è in MOTO quando varia la sua posizione rispetto al sistema di riferimento.
Un corpo è in QUIETE se la sua posizione non varia rispetto al sistema di riferimento.
Il sistema di riferimento si considera in quiete (fermo).
La traiettoria è l’insieme delle posizioni occupate dal punto materiale durante il moto (ossia la scia).
La legge oraria è una relazione che lega lo spazio percorso con l’intervallo di tempo impiegato.
Può essere espressa in tre modi:
1) Mediante un’equazione matematica, per es: s(t) = 2+3*t
2) Mediante una tabella, per es. la tabella oraria dei treni.
- Mediante un grafico in cui il tempo è posto nelle ascisse e lo spazio percorso nelle ordinate.
GRANDEZZE DEL MOTO
Le grandezze del moto sono:
1) Spazio percorso;
2) Tempo impiegato;
3) Velocità;
4) Accelerazione .
VELOCITA’ MEDIA E VELOCITA’ ISTANTANEA
La velocità media (v) è data dal rapporto tra lo spazio percorso e il tempo impiegato ed è riferita ad un intervallo di tempo più o meno grande.
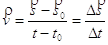
Dove (s) è l’ascissa della posizione finale al tempo (t), e (s0) è l’ascissa della posizione iniziale al tempo(t0). (Ds= s-s0) è lo spazio percorso e (Dt=t-t0) è il tempo impiegato.
La velocità si misura in 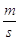 (chilometri/ore).
(chilometri/ore).
Per passare da 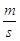 si divide per 3,6.
si divide per 3,6.
Pertanto 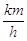
La velocità media, equivale ad una velocità costante di un corpo che impiega lo stesso tempo per percorrere la stessa distanza. La velocità media viene calcolata dall’inizio alla fine.
La velocità istantanea è la velocità calcolata in un tempo piccolissimo.
Un intervallo di tempo si può considerare piccolissimo se nella sua durata la velocità del corpo resta costante.
L’ACCELERAZIONE
Si definisce accelerazione (a) il rapporto tra la variazione di velocità ed il tempo impiegato.
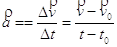
Dove: (Dv= v-v0) è la variazione di velocità e (Dt= t-t0) è il tempo impiegato.
(v) è la velocità al tempo (t) e (v0) è la velocità iniziale al tempo (t0).
L’accelerazione è una grandezza vettoriale e si misura in 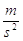
L’accelerazione, indica la rapidità con cui varia la velocità di un corpo. Si può anche definire come la variazione di velocità che si ha nel tempo unitario 1s.
Un corpo possiede accelerazione negativa quando decelera e accelerazione positiva quando accelera.
STUDIO DEI MOTI
I moti sono definiti da due aggettivi: il primo è riferito alla forma della traiettoria (rettilinea, circolare, parabolica, ellittica, ecc.); il secondo è riferito alla variazione del modulo della velocità ( uniforme, uniformemente accelerato, ecc.)
MOTO RETTILINEO UNIFORME
Moto rettilineo: moto che avviene su una traiettoria rettilinea.
Moto uniforme: moto che avviene con il modulo della velocità costante
E’ il moto che avviene sulla traiettoria rettilinea con velocità costante. Può essere anche definito come il moto di un corpo che percorre spazi uguali in tempi uguali.
La legge oraria, o equazione del moto, si ricava dalla formula di definizione della velocità (in cui si è posto t0=0):
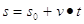
s0 è l’ascissa della posizione iniziale e 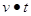 è lo spazio percorso.
è lo spazio percorso.
MOTO RETTILINEO UNIFORMEMENTE ACCELERATO
È il moto che avviene su una traiettoria rettilinea con accelerazione tangenziale costante.
L’equazione che lega il modulo della velocità (v) con il tempo impiegato (t) è la seguente:
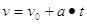
dove v0 è la velocità iniziale ed a è il modulo dell’accelerazione (costante).
L’equazione del moto (legge oraria) completa è la seguente:
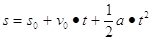
Dove s0 è l’ascissa della posizione iniziale. Se il corpo parte da fermo (v0=0) e dalla posizione di origine del sistema di riferimento (s0=0), la legge oraria si semplifica in:
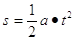
LA DINAMICA
La DINAMICA è il capitolo della fisica che studia le cause del moto, ossia studia la relazione tra forze applicate e accelerazione del corpo.
1° PRINCIPIO DELLA DINAMICA o d’inerzia
Quando la risultante delle forze applicate ad un corpo è nulla, esso o è fermo o si muove di moto rettilineo uniforme.
2° PRINCIPIO DELLA DINAMICA o principio fondamentale
L’accelerazione che una forza imprime a un corpo ha modulo direttamente proporzionale al modulo della forza e inversamente proporzionale alla massa del corpo. Forza ed accelerazione hanno la stessa direzione e lo stesso verso.
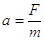
Dove (a) è l’ accelerazione, (F) è la forza applicataed (m) è la massa del corpo.
Con il secondo principio si può definire l’unità di misura della forza nel Sistema Internazionale (SI): un Newton è la forza che applicata alla massa di un chilogrammo l’accelera di un metro/secondo2 (misura dinamica della forza): 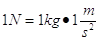
Il secondo principio è detto fondamentale perché comprende anche il primo. Infatti se la risultante delle forze applicate al corpo è nulla, si ha che anche l’accelerazione è nulla, ossia la velocità del corpo non varia. Pertanto se il corpo è fermo resta fermo e se è in moto prosegue con velocità costate (moto rettilineo uniforme).
Dal secondo principio si ha anche la relazione tra massa (m) e peso (P) di un corpo: il peso è la forza di attrazione tra un corpo e la Terra e che accelera il corpo, quando è in caduta libera, con accelerazione pari a g=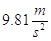 (accelerazione di gravità):
(accelerazione di gravità):
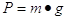
3° PRINCIPIO DELLA DINAMICA o di azione e reazione
Se un corpo esercita un’azione su un altro corpo, quest’ultimo reagisce con un’azione uguale e contraria.
IL LAVORO
Si definisce lavoro il prodotto tra la forza applicata ad un corpo e lo spostamento che esso subisce nella direzione della forza.
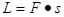
Nel sistema internazionale si misura in joule (J):
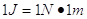 (1 Joule = 1 Newton x 1 metro).
(1 Joule = 1 Newton x 1 metro).
Il lavoro è una grandezza scalare. Esso può essere motore e resistente.
LAVORO MOTORE: se la forza è responsabile dello spostamento del corpo. Questo si ha quando l’angolo compreso tra la direzione della forza e la direzione dello spostamento è minore di 90°;
LAVORO NULLO: se la direzione della forza è perpendicolare (angolo retto) alla direzione dello spostamento. In questo caso la forza né favorisce né ostacola lo spostamento del corpo;
LAVORO RESISTENTE: se la forza si oppone al movimento del corpo.
Questo si ha quando l’angolo compreso tra la direzione della forza e la direzione dello spostamento è maggiore di 90°.
LA POTENZA
La potenza è data dal rapporto tra il lavoro (L) compiuto e l’intervallo di tempo (t) impiegato.
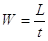 )
)
Nel Sistema Internazionale, si misura in Watt (simbolo W).
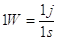 )
)
La potenza indica la rapidità con cui una macchina o un corpo compie lavoro.
Considerando che il lavoro è pari a 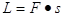
Un multiplo del watt è il chilowatt: 1kW=1000W
La potenza si misura anche in cavalli vapore (CV o HP): 1HP = 1CV =736W
L’ENERGIA
Un corpo possiede energia quando è in grado di compiere lavoro.
Per misurare l’energia posseduta da un corpo si valuta il lavoro compiuto per fargliela acquisire, oppure il lavoro che il corpo potrebbe compiere.
Tutte le volte che si compie lavoro si ha uno scambio di energia, ossia il corpo che compie lavoro cede energia ad un altro che la riceve.
L’energia in natura si presenta sotto varie forme:
ENERGIA POTENZIALE , ENERGIA CINETICA, ENERGIA ELETTRICA
ENERGIA TERMICA, ENERGIA CHIMICA
ENERGIA MAGNETICA, ENERGIA NUCLEARE ecc…
Tutti i tipi di energia, nel Sistema Internazionale, si misurano in Joule (J).
PRINCIPIO DI CONSERVAZIONE DELL’ENERGIA
L’energia né si crea e né si distrugge ma si trasforma da una forma ad un’altra.
ENERGIA POTENZIALE
L’energia potenziale è l’energia posseduta da un corpo grazie alla posizione che occupa.
ENERGIA POTENZIALE GRAVITAZIONALE
E’ l’energia posseduta dai corpi rispetto al pianeta ad esempio la Terra.
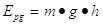
Dove (m) è la massa del corpo, g (= 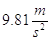 ) è l’ accelerazione gravitazionale , (h) è l’altezza rispetto ad un piano di riferimento e (Epg) è l’ energia potenziale gravitazionale.
) è l’ accelerazione gravitazionale , (h) è l’altezza rispetto ad un piano di riferimento e (Epg) è l’ energia potenziale gravitazionale.
L’energia potenziale dipende dal piano di riferimento rispetto al quale si misura l’altezza (h).
ENERGIA CINETICA
E’ l’energia posseduta da un corpo grazie alla sua velocità.
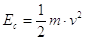
Dove(v) è la velocità del corpo, (m) è la sua massa ed (Ec) è l’ energia cinetica.
TEOREMA SULL’ENERGIA CINETICA
Il lavoro compiuto su un corpo è uguale alla variazione della sua energia cinetica.
L =DEc
Quando il corpo riceve lavoro aumenta la sua energia cinetica,
mentre se il corpo compie lavoro diminuisce la sua energia cinetica.
ENERGIA MECCANICA
Si definisce energia meccanica (Em) la somma tra l’energia potenziale gravitazionale (Epg) e l’energia cinetica (Ec) di un corpo:
Em= Epg + Ec
Se su un corpo in moto agisce solo la forza peso, l’energia meccanica del corpo è costante, ossia si conserva.
Un forza è conservativa se il lavoro compiuto in uno spostamento dipende solo dalle posizioni iniziale e finale.
Una forza è non conservativa se il lavoro compiuto dipende dal percorso seguito dal corpo.
LEGGE DELLA DILATAZIONE TERMICA LINEARE
[Pagg. 155-158]
Quando un corpo varia la sua temperatura varia anche il suo volume e le dimensioni dei suoi lati.
Se un corpo ha una dimensione molto grande rispetto alle altre due (un filo, un’asta ecc.) allora si parla di dilatazione termica lineare.
La legge della dilatazione termica lineare dice che: l’allungamento che un corpo filiforme subisce per dilatazione termica, è direttamente proporzionale alla lunghezza iniziale, alla variazione di temperatura e dipende dal materiale.
Δl=λloΔT
Dove:
- Δl è l’allungamento: Δl = l-lo= lunghezza finale – lunghezza iniziale.
- λ è il coefficiente di dilatazione termica lineare, che dipende dal tipo di materiale,i valori di questo coefficiente si trovano nelle tabelle. [pag 156]
- ΔT è la variazione di temperatura: ΔT=T-To= Tfinale – T iniziale.
Sostituendo Δl = l-lo e ricavando l si ha la formula per calcolare la lunghezza finale:
l = lo(1+ λΔT)
RELAZIONE TRA CALORE E TEMPERATURA
[Pagg. 163-170]
Quando viene fornito calore ad un corpo, se non varia il suo stato (solido, liquido, aeriforme), aumenta la sua temperatura, se invece viene raffreddato diminuisce la sua temperatura. A parità di calore scambiato (Q), la variazione di temperatura (ΔT) non è uguale per tutti i corpi, ma dipende dalla massa del corpo e dal tipo di materiale di cui è costituito.
LEGGE:
La quantità di calore che bisogna fornire ad un corpo di massa (m) è direttamente proporzionale alla variazione di temperatura(Δt), alla massa del corpo (m) e dipende dal materiale, mediante il calore specifico (C).
Q = C m ΔT
Dove: (Q) è il calore scambiato, (C) è il calore specifico [pag 166] ,(m) è la massa del corpo ,(Δt) è la variazione di temperatura:. ΔT= T-To = temperatura finale – temperatura iniziale.
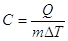 Il CALORE SPECIFICO è la quantità di calore che bisogna fornire ad un corpo di massa 1Kg per far variare la sua temperatura (T) di 1°C o 1°K.
Il CALORE SPECIFICO è la quantità di calore che bisogna fornire ad un corpo di massa 1Kg per far variare la sua temperatura (T) di 1°C o 1°K.
Il calore specifico dipende esclusivamente dal materiale di cui è costituito il corpo e non dalla massa o dal volume.
La CAPACITA’ TERMICA di un corpo è la quantità di calore che bisogna fornire a quel corpo di massa m per variare la sua temperatura di 1°C. La capacità termica viene indicata con: Ct.
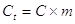
UNITA’ DI MISURA DEL CALORE
L’unità di misura del calore è la CALORIA (cal). Si usa anche la CHILOCALORIA (Kcal)
1Kcal=1000cal
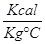 Una CHILOCALORIA è la quantità di calore necessaria per elevare la temperatura di 1Kg di acqua pura da 14,5°C a 15,5°C.
Una CHILOCALORIA è la quantità di calore necessaria per elevare la temperatura di 1Kg di acqua pura da 14,5°C a 15,5°C.
L’unità di misura del calore specifico è:
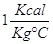
Pertanto il calore specifico dell’acqua è pari a
EQUIVALENZA TRA CALORE E LAVORO
Il calore è una forma di energia (energia termica) pertanto si misura in joule.
L’equivalenza tra caloria e joule è provata dall’esperienza di Joule, da cui risulta:
1Kcal=4186J 1cal=4,186J 1Kcal=1000cal
CAMBIAMENTI DI STATO
Stati di aggregazione della materia
Un corpo:
- è allo stato solido se ha volume e forma propria;
- è allo stato liquido se ha volume proprio e forma del recipiente che lo contiene;
- è allo stato aeriforme se ha forma e volume del recipiente che lo contiene.
Liquidi ed aeriformi sono detti anche fluidi.
SCHEMA RIASSUNTIVO DEI PASSAGGI DI STATO:
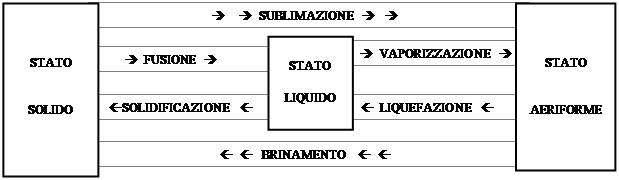
LEGGI DELLA FUSIONE E DELLA SOLIDIFICAZIONE
1) Ogni sostanza fonde a una determinata temperatura che è la stessa di solidificazione.
2) La temperatura di fusione, o di solidificazione, è una caratteristica della sostanza e non dipende dalla massa.
3) Durante la fusione, o la solidificazione, la temperatura si mantiene costante fino a trasformazione ultimata.
4) per fondere una massa unitaria (1kg) di sostanza occorre una quantità di calore detto calore di fusione (viene anche detto calore latente di fusione), che dipende dalla sostanza di cui è costituito il corpo.
LEGGI DELL’EBOLLIZIONE
1) L’ebollizione è un processo di vaporizzazione che interessa tutta la massa liquida e non solo lo strato superficiale.
2) Un liquido bolle a una temperatura detta punto di ebollizione che dipende dalla sua natura e dalla pressione esterna, ma non dalla sua massa.
3) La tensione del vapore saturo del liquido alla temperatura di ebollizione è uguale alla pressione esterna agente su di esso.
4) Durante l’ebollizione, se non cambia la pressione esterna, la temperatura del liquido si mantiene costante fino a completa vaporizzazione.
5) Per vaporizzare una massa unitaria di liquido (1kg), preventivamene portata al punto di ebollizione, occorre una certa quantità di calore, che prende il nome di calore di vaporizzazione e che dipende dalla natura del liquido.
ELETTRIZZAZIONE
Un corpo possiede una carica elettrica quando ha un eccesso o un difetto di elettroni.
Un corpo possiede una carica positiva quando sono in difetto gli elettroni; possiede invece carica negativa, quando sono in eccesso gli elettroni.
La carica elettrica si misura in coulomb (C).
Ci sono tre modi per elettrizzare un corpo:
1) PER STROFINIO
2) PER CONTATTO
3) PER INDUZIONE O POLARIZZAZIONE
L’elettrizzazione per induzione, si ha nei corpi conduttori;
L’elettrizzazione per polarizzazione, si ha nei corpi isolanti.
I corpi sono:
1) ISOLANTI (O DIELETTRICI) se non permettono lo spostamento di cariche elettriche (elettroni) nel loro interno.
2) CONDUTTORI se permettono il passaggio di corrente nel loro interno.
FORZE ELETTRICHE e LEGGE DI COULOMB
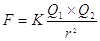 Due cariche elettriche puntiformi si attraggono o si respingono con una forza diretta secondo la loro congiungente, di intensità direttamente proporzionale al loro prodotto e inversamente proporzionale al quadrato della loro distanza.
Due cariche elettriche puntiformi si attraggono o si respingono con una forza diretta secondo la loro congiungente, di intensità direttamente proporzionale al loro prodotto e inversamente proporzionale al quadrato della loro distanza.
Dove:
- (F) è la forza di interazione tra le cariche, misurata in Newton (N). F è positiva se di repulsione, negativa se di attrazione.
- (K) è la costante di Coulomb e per cariche poste nel vuoto vale Ko= 9*109 N*m²/C².
- (Q1 Q2) sono le due cariche elettriche, che si misurano in Coulomb (C). Esse devono essere inserite nella formula con il loro segno positivo o negativo.
- (r) è la distanza tra le cariche elettriche, misurata in metri (m).
Due cariche dello stesso segno (+ e+; - e -) si respingono, cariche con segno diverso si attraggono.
INTENSITA’ DI CORRENTE ELETTRICA
La corrente elettrica è un movimento ordinato di cariche elettriche.
L’intensità di corrente elettrica (i), indica la carica (q) che attraversa una sezione di un conduttore nell’unità di tempo (t).
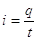
L’intensità di corrente è una grandezza fondamentale e si misura in ampere.
L’amperometro è uno strumento che misura l’intensità di corrente elettrica. In un circuito va sempre collegato in serie.
Il voltmetro o voltometro, è lo strumento che misura la differenza di potenziale elettrico. In un circuito va sempre collegato in parallelo.
1a LEGGE DI OHM
La differenza di potenziale (V) ai capi di una resistenza elettrica è direttamente proporzionale all'intensità di corrente (i) che vi circola.
V=R*i
R=V/i
Dove (R) è la resistenza elettrica (costante).
La costante di proporzionalità è la resistenza elettrica del conduttore. Essa si misura in ohm (simbolo W)
La resistenza elettrica dipende dalla forma geometrica del conduttore e dal tipo di materiale di cui è costituito; dipende anche dalla temperatura del conduttore.
Gli utilizzatori di un circuito dotati di resistenza elettrica sono detti resistori.
2a LEGGE DI OHM
La resistenza elettrica di un conduttore metallico filiforme è direttamente proporzionale alla sua lunghezza (l), inversamente proporzionale all’area (A) della sua sezione e dipende dalla resistività (ρ) del materiale.
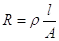
La resistività dipende dal tipo di materiale del conduttore.
COLLEGAMENTO DELLE RESISTENZE
Le resistenze possono essere collegate in serie e in parallelo.
COLLEGAMENTO IN PARALLELO:
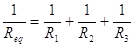
COLLEGAMENTO IN SERIE:
Req = R1 + R2 + R3
ENERGIA E POTENZIALE ELETTRICA
L’energia elettrica è data dal prodotto tra la differenza di potenziale, l’intensità di corrente ed il tempo:
Energia elettrica: ε =V * i * t
La potenza elettrica è data dal prodotto tra la differenza di potenziale e l’intensità di corrente elettrica:
Potenza elettrica: W =V * i
ENERGIA ELETTRICA IN UNA RESISTENZA: EFFETTO JOULE
L’energia elettrica in una resistenza è dissipata (trasformata) in calore.
Effetto JOULE : La quantità di calore che si sviluppa in una resistenza (R) è direttamente proporzionale al quadrato dell’intensità di corrente (i) che vi circola e al tempo (t):
Q = R * i² * t
Fonte: http://www.ipssceinaudi.it/materialedidattico/APPUNTI%20DI%20FISICA%20PROF%20DI%20RUZZA.doc
autore: PROF DI RUZZA
Fisica appunti
Visita la nostra pagina principale
Fisica appunti
Termini d' uso e privacy