Baricentro e leve

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Baricentro e leve

BARICENTRO
Peso e baricentro
Gli esperimenti sulle sagome appese e gli oggetti sul piano sono utili per introdurre un’altra particolarità della forza: il punto di applicazione. Questi esperimenti sono anche esempi di una fisica applicata a corpi estesi, aspetto che non era stato preso in considerazione precedentemente.
I ragazzi potrebbero pensare che il baricentro sia sempre all'interno di un corpo. Qualche opportuna domanda potrà rivelare il loro pensiero e una serie di esperimenti, atti a mettere in crisi le opinioni che via via emergono dalla discussione, renderà chiaro il concetto che la posizione del baricentro dipende dalla distribuzione delle masse e può anche essere esterno a un oggetto.

Esperimento: Come trovare il baricentro?
Scopo: si può trovare il baricentro di un cartoncino sagomato, assimilabile ad una figura piana
Materiale: filo a piombo, chiodo, compasso, squadra, superficie verticale per fissare il chiodo, un altro spago, cartoncino forbici, martello
Procedimento: sospendendolo per due diversi punti: le verticali per tali punti si intersecano nel baricentro. Un corpo appeso si dispone infatti in una posizione di equilibrio stabile e il baricentro del corpo si trova pertanto sempre sulla verticale sotto al punto di sospensione
Disegnare sul cartoncino un cerchio (compasso), un rettangolo (squadra) e una figura irregolare e poi ritagliarli.e praticare lungo il bordo di ogni figura due fori.
Fissare sulla superficie verticale il chiodo e appendere una delle figure ritagliate utilizzando uno dei fori e il filo a piombo: tracciar con la matita la linea indicata dal filo a piombo. Appendere la stessa figura per l’altro foro e tracciare la linea indicata dal filo a piombo, tracciare con la stessa procedura due linee sulle altre due figure.
Se sospendiamo l’oggetto mediante un filo fissato nel punto prima individuato, esso sta in equilibrio.

Osservazioni: Cosa accade? Le figure restano immobili, perché sono appese per il loro baricentro! Si deduce che la forza esercitata dal filo equilibra una forza che è la somma, se immaginiamo di dividere l’oggetto in tante piccole parti, dei pesi di tutte queste parti e che è quindi il peso totale dell’oggetto. Il punto individuato si chiama baricentro, che risulta essere, appunto, il punto di applicazione del peso dell’oggetto.

Quale riga cade prima?
Il fatto che un bambino sia più soggetto di un adulto a cadere a terra quando inciampa ha una spiegazione scientifica. L’adulto, poiché il suo baricentro è più alto, cade più lontano e quindi ha più tempo per riprendersi. Per oggetti simili più è alto il baricentro e più tempo impiega a cadere…per esempio si può fare una “gara di caduta” tra righe di lunghezza diversa. Mettere le due righe in piedi su una estremità, a fianco a fianco, e lasciare cadere nello stesso istante: vincerà la più corta. Si può poi dimostrare che il tempo di caduta dipende davvero dal baricentro e non dall’altezza reale dell’oggetto si può dimostrare ripetendo l’esperimento dopo aver appesantito la riga più lunga vicino all’estremità inferiore: questa volta vincerà la riga più lunga!

Baricentro alto e baricentro basso

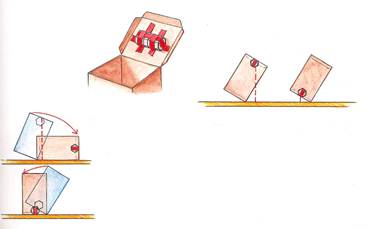Materiale: scatola di cartone a base quadrata con alette per chiuderla, peso di circa 30 g, nastro adesivo.

Procedimento: aprire la scatola e sull’aletta che fa da coperchio fissa il peso con il nastro adesivo e poi richiudila. Appoggia la scatola su un piano in modo che il peso si trovi in alto e spingila per inclinarla fino a farla cadere, capovolgi la scatola in modo che il peso sia in basso e spingila per farla cadere ancora.

Commento e conclusione
Con il peso in alto una piccola spinta è sufficiente per far cadere la scatola, con il peso in basso la spinta deve essere più forte, altrimenti la scatola si inclina molto ma torna alla posizione di partenza.
Quando il baricentro è in alto è sufficiente una piccola spinta per far sporgere il baricentro oltre la base di appoggio e la scatola cade. Se il peso è basso ci vuole una spinta maggiore per farlo uscire dalla base di appoggio.
Le automobili come gli altri veicoli sono costruiti in modo che il baricentro rimanga sempre tra le ruote e ci siano poche possibilità di rovesciamento in caso di incidente. Per questo il motore che è molto pesante viene messo in basso soprattutto nei veicoli alti.

Una scatola che rotola in salita
Appesantendo una scatola rotonda in modo che il suo centro di gravità si trovi sul bordo, invece che nel centro, com’è naturale, si può far rotolare una scatola in salita o in discesa. Il trucco è una striscia di piombo tagliata da un vecchio tubo. Piegare la striscia a forma di J e fissarla a cavallo del bordo della scatola aperta. Quando si richiude il coperchio segnare la posizione del peso. Per far rotolare la scatola in discesa mettere la scatola su un piano inclinato in modo che il peso sia in alto ma spostato verso la parte del piano in discesa. Per far andare la scatola in salita (in senso contrario alla legge di gravità!) collocare la scatola con il peso in alto lievemente spostato verso la parte del piano in salita. La lunghezza del piano deve essere tale che la scatola raggiunga la sommità proprio quando il peso è sceso in fondo.

La scatola magica
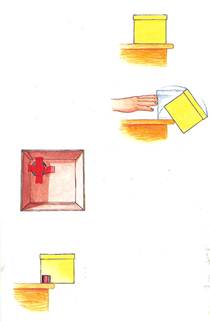
Materiale: una scatola di cartone con coperchio, delle monete, nastro adesivo, un tavolo su cui lavorare.

Procedimento: Appoggiare la scatola vicino al bordo e spostarla gradualmente in modo che sporga sempre più.

Commento e conclusione
Quando il punto centrale della base supera la base di appoggio (cioè il bordo del tavolo), la scatola cade.
Aprire la scatola e fissare le monete con il nastro adesivo e richiuderla.
Appoggiare la scatola al tavolo e ripetere l’esperimento.
La scatola non cade anche se il punto centrale supera il bordo del tavolo.
Finché l’angolo con le monete è appoggiato al tavolo la scatola rimane in equilibrio.

Quando la scatola è vuota il baricentro è al centro e se questo esce dalla base di appoggio (il tavolo) la scatola cade perché la forza di gravità agisce su questo punto. Quando metti le monete nell’angolo spostano il baricentro, per cui la scatola rimane in equilibrio finché quel punto si trova sulla base di appoggio.

Perché cadiamo?
Il corpo umano ha un baricentro che è situato all’incirca all’ombelico, se esso rimane entro la base di appoggio (tra i due piedi) il corpo è in equilibrio, se si sposta al di fuori cade. Quando siamo seduti il baricentro è molto spostato ma la sedia impedisce di cadere. Prova ad alzarti senza mettere i piedi sotto la sedia e tenendo lo braccia lungo i fianchi: impossibile! Per alzarsi l ‘unico modo è mettere i piedi sotto la sedia oppure mettere le braccia avanti. I bambini piccoli fanno fatica ad alzarsi proprio perché hanno una piccola base di appoggio.

EQUILIBRIO
I ragazzi vengono invitati a disporre alcuni oggetti in equilibrio. L’insegnante fa altrettanto. Si discute sul significato che viene attribuito alla parola "equilibrio", per poi precisare quello usato in un linguaggio scientifico.
Equilibrio e forze
Esperimento: il tiro alla fune e altro…
Anche per questo argomento si comincia con un gioco: il tiro alla fune. Se le squadre tirano la fune con la stessa forza, si ha equilibrio.

Dal gioco si passa al semplice esperimento del fermaglio tra due elastici.
L’attrezzatura può essere costruita dai ragazzi.
Il fermaglio viene mantenuto in equilibrio, cioè fermo, da due elastici uguali, deformati allo stesso modo. Ciò conferma che, per mantenere in equilibrio un oggetto su cui agiscono due forze, queste devono essere uguali ed opposte.

Se un oggetto è in equilibrio appeso ad una molla vuol dire che anche la molla fa forza. In questo modo si sottolinea il fatto che per mantenere un oggetto in equilibrio occorrono almeno due forze. Si propongono situazioni di equilibrio di oggetti tirati da due forze, per far notare che l’equilibrio viene mantenuto se le due forze hanno la stessa intensità, uguale retta di azione e verso opposto.

Corpo in equilibrio sotto l'azione di due forze Qualunque sia la forza con cui si tira un oggetto, quella che lo mantiene in equilibrio lungo la stessa direzione è uguale ed opposta. Due dinamometri aventi le stesse caratteristiche attaccati ad un fermaglio lungo una guida vengono allungati dello stesso tratto.

Esperimento: Equilibrio con due forze che spingono
Una palla di gomma piuma fa sperimentare l’equilibrio di forze che premono: esse devono essere uguali perché la palla stia ferma..La palla è in equilibrio tra due forze opposte. Le forze deformano la palla allo stesso modo. Ciò conferma che le due forze hanno lo stesso valore.

Esperimento: i vincoli…forze che sostengono!
Equilibrio su un piano solido
Un corpo appoggiato
Un oggetto appoggiato su un piano orizzontale è in equilibrio perché il piano esercita una forza, una reazione vincolare opposta al peso del corpo.

Procedimento
Si appoggia l’oggetto sul piano. Si constata la situazione di equilibrio.
Sull’oggetto agisce la forza peso, che da sola non potrebbe mantenere l’oggetto in equilibrio. Basta togliere il sostegno e l’oggetto cade. Il sostegno quindi esercita forze che mantengono l’oggetto in equilibrio.
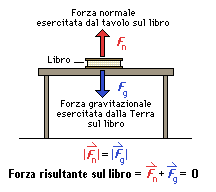Questa premessa porta ad introdurre, attraverso l’analisi di situazioni concrete, una forza particolare, la forza esercitata dal vincolo (tavola o altro elemento che sorregge l’oggetto).

Si osserva un oggetto su un tavolo. E’ in equilibrio? Allora quante forze ci sono? Quali forze? Non ci sono effetti visibili, ma certamente tangibili: solleviamo l’oggetto, esso pesa; premiamo sul tavolo, esso resiste, fa forza su di noi. Sull’oggetto agisce la forza peso, che da sola non potrebbe mantenere l’oggetto in equilibrio. Basta togliere il sostegno e l’oggetto cade. Il sostegno quindi esercita forze che mantengono l’oggetto in equilibrio. Un oggetto appoggiato su un piano orizzontale è in equilibrio perché il piano esercita una forza, una reazione vincolare opposta al peso del corpo.

Proviamo a ripetere l’esperimento sistemando due scatole di scarpe a 10 cm di distanza, appoggiando sui coperchi un cartoncino e sopra questo, in corrispondenza dello spazio tra le scatole l’oggetto. Il cartoncino si piega perché non riesce a contrastare la forza di gravità che attira il bicchiere verso il basso. Mettere un secondo cartoncino sotto il precedente e osservare cosa accade.

Equilibrio in un liquido: Si mette un ovetto nell’acqua contenuta in un recipiente trasparente. Galleggia. Ci sono forze? Sfruttiamo l’analogia con l’esperimento precedente, per arrivare a far concludere che le forze sono almeno due: il peso dell’ovetto e la forza che lo sostiene.

Equilibrio in un gas: Ma anche il palloncino galleggia nell’aria. Anche l’aria fa come l’acqua. Il palloncino è salito in alto, quasi tocca il soffitto, rimane sospeso trattenuto da un filo legato ad un sostegno. Quante forze ci sono sul palloncino? Il peso, la forza di sostegno dell’aria, quella del filo legato al sostegno: tre forze. Anche tre forze possono tenere un oggetto in equilibrio e anche più di tre, ma mai una sola.

Il peso appeso: il dado appeso alla molla è in equilibrio. C’è la forza peso del dado. Se il dado non fosse appeso alla molla, non sarebbe in equilibrio, perché cadrebbe; quindi c’è, anche in questo caso, una seconda forza, opposta ed uguale al peso, esercitata dalla molla, che possiamo chiamare forza elastica.

La macchinina sullo scivolo mostra che il piano in discesa non è più in grado di sostenerla e occorre agganciarla ad un elastico fissato al bordo dello scivolo. Ma il piano non dà nessun contributo? Basta inclinarlo diversamente per far constatare come la tensione dell’elastico vari e così mettere in evidenza il contributo del piano. La macchinina è in equilibrio su uno scivolo. Anche in questo caso ci sono tre forze: il peso della macchinina, la forza elastica dell’elastico che la trattiene e la forza di sostegno del tavolo.

Un’automobilina posta sul piano inclinato viene tenuta ferma da un dinamometro parallelo al piano. La forza misurata dal dinamometro cresce con l’inclinazione del piano: è pari al peso dell’automobilina quando il piano è verticale e l’automobilina è appesa; diventa zero quando il piano è orizzontale.

Al posto dell’elastico…l’attrito! Sullo scivolo c’è ora un piccolo aeroplano; è in equilibrio senza essere trattenuto dall’elastico. Si nota che il piano di appoggio è ruvido. La ruvidità del piano produce una forza (attrito), che assieme alla forza peso e alla forza del sostegno mantiene in equilibrio l’aeroplanino, che non scivola giù (e neppure decolla da questa rampa di lancio!).

Equilibrio

1. La tartaruga è appoggiata sul tavolo e rimane ferma, in equilibrio. Quali sono le forze agenti sulla tartaruga?
nessuna
solo la forza peso
due forze aventi risultante nulla, il peso della tartaruga e la forza del tavolo
solo la forza del tavolo

2. Un fermaglio è mantenuto fermo in posizione orizzontale da due molle tese. Se si aumenta la tensione (l’allungamento) di una molla:
anche l’altra molla si allunga, ma di meno
anche l’altra si allunga, della stessa quantità
l’altra molla resta della stessa lunghezza

3. Si provi ora a variare la pendenza del piano inclinato, spostando il fermo. Si osservi attentamente l’indicazione del dinamometro e la sua direzione per ogni angolo realizzabile, anche nei casi in cui il piano è inclinato di 0° (piano orizzontale) o di 90° (piano verticale).
Si compili poi la tabella seguente.

INCLINAZIONE DI 0°

Direzione del dinamometro:
orizzontale
verticale
inclinata rispetto al piano
orizzontale

Intensità della forza misurata:
 massima
 nulla
 intermedia

L’automobilina è in equilibrio?
 si
 no
 non so

Quante sono le forze agenti?
 una
 due
 più di due

INCLINAZIONE DI 90°

Direzione del dinamometro:
 orizzontale
 verticale
inclinata rispetto al piano
orizzontale

Intensità della forza misurata:
 massima
 nulla
 intermedia

L’automobilina è in equilibrio?
 si
 no
 non so

Quante sono le forze agenti?
 una
 due
 più di due

INCLINAZIONE QUALSIASI

Direzione del dinamometro:
 orizzontale
 verticale
 inclinata rispetto al piano
orizzontale

Intensità della forza misurata:
 massima
 nulla
 intermedia

L’automobilina è in equilibrio?
 si
 no
 non so

Quante sono le forze agenti?

una
due
più di due

INCLINAZIONE DI 0°

Quali sono le forze agenti?
 il peso
 la reazione del piano
 la forza di richiamo della
molla del dinamometro

La reazione del piano:
 non c’è
 è sempre opposta al peso
 è perpendicolare al piano

INCLINAZIONE DI 90°

Quali sono le forze agenti?
 il peso
 la reazione del piano
 la forza di richiamo della
molla del dinamometro

La reazione del piano:
 non c’è
 è sempre opposta al peso
 è perpendicolare al piano

INCLINAZIONE QUALSIASI

Quali sono le forze agenti?
 il peso
 la reazione del piano
 la forza di richiamo della
molla del dinamometro

La reazione del piano:

non c’è
è sempre opposta al peso
è perpendicolare al piano

3a. In quale dei tre casi appena considerati si realizza un equilibrio con più di due forze?
 inclinazione di 0°
 inclinazione di 90°
 inclinazione intermedia

3b. Perchè ci sia equilibrio è necessario avere:
 una forza
 due forze
 almeno due forze

4. Poggiando su un piano inclinato la tartaruga, senza trattenerla con il dinamometro, si faccia in modo che resti ferma, in equilibrio.

4a. Quali e quante forze agiscono sulla tartaruga?
.................................................................................................................................................

.................................................................................................................................................

4b. Come mai non cade?
................................................................................................................................................

.................................................................................................................................................

Equilibrio per rotazione degli oggetti
Equilibrio di un'asta girevole: le leve
Perché i ragazzi svolgano questo esperimento in maniera quantitativa, è preferibile usare materiale di laboratorio oppure materiale costruito con attenzione: l’asta deve essere omogenea, l’articolazione perno e foro deve avere il minimo attrito, i fori di sospensione ben centrali, i pesetti devono essere uguali.
I ragazzi devono sospendere l’asta al sostegno infilando il perno in uno dei fori centrali e poi nell’altro. Si chiede loro se riconoscono una diversità nelle due situazioni di equilibrio. Si discute fino a stabilire una sorta di regola: se il perno di sospensione è…., altrimenti….. Si chiede poi di mettere l’asta in modo tale che rimanga orizzontale. Si lavora con i pesi fino a individuare la relazione tra pesi e distanza.

Esperimento: Equilibrio di oggetti appoggiati non omogenei

Ovetti con la stessa forma e le stesse dimensioni stanno in equilibrio su un piano orizzontale in posizioni diverse. In ogni ovetto è stato aggiunto un sovrappeso in posizione diversa. Essi hanno pertanto i baricentri in posizioni diverse. Se vengono spostati dalla posizione di equilibrio tendono a riassumerla. Ogni oggetto tende ad assumere la posizione che minimizza l’energia potenziale del sistema e realizza una condizione di equilibrio stabile, per la quale il baricentro risulta nel punto più basso possibile.

Procedimento: Si aprono i contenitori e si sistema al loro interno della plastilina appesantita da un piombino, facendola aderire alla parete in punti diversi nei vari recipienti. Richiusi gli oggetti, questi vengono appoggiati su un tavolo. Si nota che essi assumono una ben determinata posizione di equilibrio, legata alla posizione della parte appesantita. Se vengono rimossi da tale posizione, tendono a tornarvi

Ovetti in equilibrio

1. Si osservino gli ovetti appoggiati sul tavolo. Sono apparentemente uguali. Prendendoli in mano ed osservandoli attentamente, si può ancora affermare che sono uguali? Per che cosa differiscono?

.................................................................................................................................................

.................................................................................................................................................
2. Questo suggerisce una spiegazione alle loro diverse posizioni di equilibrio?

.................................................................................................................................................

.................................................................................................................................................
3. Si provi a spostare gli ovetti dalle loro posizioni di equilibrio. Cosa succede?

.................................................................................................................................................

.................................................................................................................................................
4. Capovolgendo l’ovetto 2 si riesce a metterlo in equilibrio. In cosa differisce il suo comportamento da quello dell’ovetto 1? Provare.

.................................................................................................................................................

.................................................................................................................................................
5. Si consideri ora l’ovetto 3: quante possibili posizioni di equilibrio si possono avere?

.................................................................................................................................................

CONCLUSIONI
6. Dobbiamo distinguere tre diverse condizioni di equilibrio, che possiamo chiamare di equilibrio stabile, instabile e indifferente. Scrivi nella casella il numero dell’ovetto che ha il comportamento descritto.

L’ovetto __________ spostato dalla posizione di equilibrio, comincia ad oscillare intorno a tale posizione. L’equilibrio è stabile.

L’ovetto __________, spostato dalla posizione di equilibrio, si allontana da tale posizione. L’equilibrio è instabile.
L’ovetto _________, spostato dalla posizione di equilibrio, si trova ancora in equilibrio. L’equilibrio è indifferente.

L’ovetto _________, è in equilibrio stabile, instabile o indifferente? _______________

7. Da cosa dipende la posizione di equilibrio?

.................................................................................................................................................

.................................................................................................................................................
8. Quale oggetto di uso quotidiano o quale giocattolo fa venire in mente quello che si è osservato?

.................................................................................................................................................
.
................................................................................................................................................

.................................................................................................................................................

Esperimento: Equilibrio di una guida omogenea

Inseriamo il perno fissato al sostegno nel foro centrale dell’asta, quello che corrisponde al centro di simmetria. L’asta assume infinite posizioni di equilibrio.
Si spiega questo fatto considerando che sull’asta agiscono due forze: quella del sostegno e la forza peso; queste forze si annullano sempre.

Esperimento: Asta con sovrappesi
Si sistema l’asta con il perno nel foro centrale sopra il baricentro. L’asta è in equilibrio in posizione orizzontale. Sistemiamo lo stesso numero di oggetti a ugual distanza dal punto di sospensione. L’asta rimane in equilibrio in posizione orizzontale. Togliamo un oggetto da una parte e l’equilibrio orizzontale si perde. Facendo altre prove, si potrà notare che distanze dal punto di sospensione dell’asta e numero di oggetti sono tra loro correlati.

Sistemiamo un oggetto alla tacca 10 del lato sinistro. Sul lato destro, per avere l’equilibrio, si possono avere le seguenti disposizioni:

distanza	10	5	2
n. oggetti	1	2	5

Il prodotto tra distanza e numero oggetti è costante. L’esperimento è una conferma della relazione teorica sull’equilibrio dei corpi rigidi girevoli intorno ad un perno. La relazione puo’ essere espressa nel nostro caso così: I prodotti della forza e la distanza della sua retta d’azione dal punto di sospensione (fulcro) devono essere uguali nei due bracci dell’asta.

Dati dell'utente

Età

Scuola

maschio
femmina

La bilancia

1. Si appenda un pupazzetto a uno dei chiodi sull’asta. Cosa succede?

................................................................................................................................................

....................................………………………………………………………………………………

2. Per ripristinare l’equilibrio si deve appendere un altro pupazzetto:
(barrare tutte le opzioni che si ritengono adeguate )

A di ugual peso B di peso maggiore

C dalla stessa parte

D dall’altra parte E alla stessa distanza

F ad una distanza maggiore
G dalla parte opposta dell’asta

H ad una distanza minore I di minor peso

3. Usando un pupazzetto di peso doppio, cosa si deve fare per ripristinare l’equilibrio?

 metterlo alla stessa distanza del primo dal punto di sospensione dell’asta

 metterlo a una distanza doppia del primo dal punto di sospensione dell’asta

 metterlo a metà della distanza del primo dal punto di sospensione dell’asta

CONCLUSIONI

4. Perché l’asta stia in equilibrio, quali condizioni si devono verificare?

.................................................................................................................................................

Esperimento: Corpi di forma irregolare girevoli attorno ad un punto - Le forze dei muscoli
Le sagome di parti del corpo sono vincolate in un punto e sostenute in posizione orizzontale con un dinamometro applicato in un altro punto. L’equilibrio dei momenti che si realizza con il dinamometro quando si aggiunge in un punto della sagoma un pesetto permette di capire il tipo di forza esercitata dai muscoli nelle diverse situazioni.

Perché le funi si spezzano sotto l’azione di carichi leggeri?
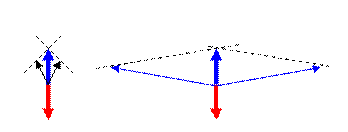Perché le corde per stendere i panni e le funi che reggono le amache si spezzano spesso anche sotto l’azione di carichi leggeri? Una causa è facile da individuare: legate insieme due elastici e nel punto di unione fissate un oggetto leggero, tenendo gli elastici quasi paralleli il peso li allunga a mala pena, divaricando gli elastici l’allungamento diventa appena maggiore ma se si tenta di disporre gli elastici in linea retta si ottiene un risultato sorprendente: non si può allungarli ulteriormente perché le forze necessarie per sostenere il peso diventano molto grandi e gli elastici si spezzano facilmente!

Seggiolini a catena
Materiale: gruppo di 10 bambini più o meno della stessa altezza
Procedimento: i bambini devono mettersi in cerchio, uno dietro le spalle dell’altro, quando viene dato il via ogni bambino piega le gambe e si siede sulle ginocchia del bambino dietro, è importante che i movimenti avvengano insieme.
Osservazione: si crea una struttura stabile e nessuno cade…il peso di ogni bambino infatti è sostenuto dalle ginocchia di quello dietro come se fosse appoggiato a una sedia.

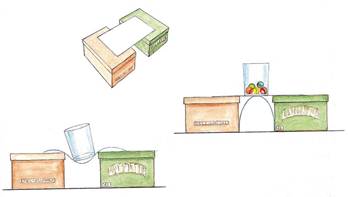Un sostegno resistente
Materiale: due cartoncini leggeri, un bicchiere largo, biglie, due scatole di scarpe
Procedimento: sistemare le scatole a 10 cm di distanza, appoggiare sui coperchi un cartoncino e sopra questo, in corrispondenza dello spazio tra le scatole il bicchiere. Il cartoncino si piega perché non riesce a contrastare la forza di gravità che attira il bicchiere verso il basso. Mettere il secondo cartoncino sotto il precedente tra le due scatole in modo che si formi un arco e che la parte centrale dei cartoncini sia a contatto. Appoggia il bicchiere e metti all’interno le biglie. La nuova struttura sostiene il peso del bicchiere e quello delle biglie. La nuova struttura ad arco è molto resistente e se sollecitata non si piega ma si comprime, per questo gli archi sono utilizzati per la costruzione di ponti edifici e dighe.

Bracco di ferro col sale
Materiale: tubo di vetro spesso o di metallo di circa 12 mm di diametro e 30 cm di lunghezza, una bacchetta di legno lievemente più lunga che si adatti liberamente al tubo, sale, tovagliolo di carta e elastico.
Chiudere una estremità del tubo con due strati di carta fissandola con l’elastico, versate nel tubo circa 8 cm di sale e inserire la bacchetta, sfidate ora a spingere fuori il cappuccio di carta premendo in maniera regolare sulla bacchetta di legno. Se il cappuccio è stato chiuso bene non si sposterà. La forza verso il basso esercitata dalla bacchetta è trasportata in gran parte dalle molecole del sale in forze dirette obliquamente e trasversalmente per cui la maggior parte della spinta è sostenuta dalla parete del tubo. Per lo stesso motivo la sabbia arresta in modo efficace i proiettili e la terra al di sopra delle gallerie e delle metropolitane si sostiene da sola!

Baricentro e leve