Fenomeni magnetici

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Fenomeni magnetici

I fenomeni magnetici sono prodotti dalle correnti elettriche e, tra i fenomeni magnetici c'è la creazione di forze elettromotrici, quindi di correnti elettriche.
Analizziamo il campo magnetico prodotto da un filo percorso da una intensità di corrente I.
Utilizziamo come sonda un ago magnetico sospeso. La sonda assume orientazioni diverse a seconda della posizione. L'inviluppo delle rette che rappresentano la direzione dell'asse dell'ago magnetico, dà luogo a circonferenze, concentriche con il filo percorso dalla corrente I, che stanno su piani ad esso perpendicolari. Sono le linee di forza magnetiche, linee cioè che indicano, per ogni punto la direzione ed il verso del campo magnetico che orienta l'ago: la direzione è quella della tangente alla linea nel punto, il verso quello uscente dal Nord dell'ago.
Il verso della corrente ed il verso della linea di forza magnetica sono associati secondo la regola del pugno destro come mostrato in figura (le dita chiuse sono concordi con il verso sulla linea)

Possiamo anche sperimentare che su linee maggiormente distanti dal filo, l'intensità della coppia che orienta l'ago è minore. Se osserviamo che la corrente I necessariamente si sviluppa in un percorso chiuso, possiamo affermare che linee di corrente (che sono le linee di forza del campo elettrico nel conduttore) sono concatenate con le linee di forza magnetiche.
In ogni punto dello spazio definiremo un vettore H, chiamato campo magnetico, che ha direzione e verso coincidenti con quello della tangente alla linea di forza passante per quel punto ed intensità proporzionale alla coppia che orienta l'ago-sonda; in pratica proporzionale all'intensità di corrente ed inversamente proporzionale alla distanza dal filo, o, ciò che è lo stesso, inversamente proporzionale alla lunghezza della circonferenza che corrisponde alla linea di forza che passa per quel punto. In definitiva:
H=I/2pd
Avremmo potuto pervenire allo stesso con il teorema di Ampere. Esso lega il campo magnetico alle correnti elettriche ricorrendo al concetto matematico di circuitazione di un vettore. Il teorema afferma che la circuitazione del campo H è uguale alla totale intensità di corrente che attraversa la linea utilizzata per il calcolo della circuitazione.
Per semplicità enunceremo il teorema in questo modo: si consideri una qualsiasi linea di forza magnetica e la si suddivida in n parti in ciascuna delle quali possa essere ritenuto H costante. Eseguendo la somma degli n prodotti HiDli dove Dli è la lunghezza dell'i-esima porzione di linea ed Hi il campo costante, si ottiene la somma algebrica delle intensità di corrente che attraversano la linea di forza.
Sono considerate positive le intensità di corrente il cui verso convenzionale è associato al verso della linea di forza come il senso di avanzamento di una vite destrogira rispetto al verso di rotazione. Sinteticamente
SHiDli=SaI (i=1...n)
Applicando questo teorema alla configurazione già esaminata, essendo H di intensità costante in ogni punto di una linea di forza, lo si può raccogliere a fattor comune e scrivere
HSDli=I (i=1...n)
ma SDli non è altro che la lunghezza della circonferenza e, se indichiamo con d la distanza del punto dal filo, cioè il raggio della linea di forza, possiamo concludere di nuovo con H*2pd=I.
La struttura tecnicamente più significativa per creare campi magnetici è il solenoide.
Immaginiamo di avvolgere del filo conduttore su un supporto prismatico. Il numero di giri completi effettuati con il filo è il numero di spire N del solenoide. Se stabiliamo una corrente nel filo avvolto, si ottiene un campo magnetico le cui linee di forza sono qualitativamente rappresentate nella figura dove è mostrato anche il modo pratico di individuare il verso delle linee magnetiche: chiudendo la mano destra con le dita (mignolo, anulare, medio, indice) nel senso della corrente convenzionale (in figura uscente rosso, entrante azzurro) il pollice indica il verso positivo delle linee di forza magnetica, in altre parole il polo Nord del solenoide.

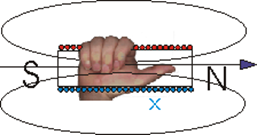
Consideriamo una linea di forza che si concatena con la totalità delle spire e suddividiamola in due parti: una interna alle spire ed una esterna.

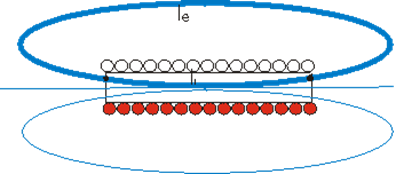
Se con Hi indichiamo il campo magnetico che supponiamo costante nel percorso interno di lunghezza li e con He il campo esterno che supponiamo costante per tutta la lunghezza le possiamo scrivere per il teorema di Ampere:

Hili+Hele=SaI
se si può ritenere He*le = 0, ipotesi valida per i solenoidi lunghi (li/d>10 con d diametro delle spire), essendo la somma algebrica delle correnti pari a N*I dove I è la corrente nelle N spire, si ha
Hili=NI
cioè
H=NI/l essendo H=Hi, l=li
Il campo magnetico interno ad un solenoide lungo è proporzionale all'intensità di corrente che percorre le spire e la costante di proporzionalità è il numero di spire per unità di lunghezza.
Allo stesso tipo di relazione saremmo giunti analizzando un avvolgimento toroidale.

Le spire sono uniformemente avvolte su un supporto a forma di ciambella, toro in matematica. Le linee di forza sono circonferenze con lo stesso centro del toro, tutte interne alle spire. Se si considera la linea di forza media (azzurra nel disegno) di raggio Rm=(Ri+Re)/2, osservando che per ragioni di simmetria il campo magnetico H ha lo stesso valore in ogni punto si può scrivere, sempre per il teorema di Ampere, 2pRmH=NI cioè ancora
H=IN/l
( l=2pRm è la lunghezza della linea di forza)
che definisce ancora la dipendenza di H dalla I e dal numero di spire per unità di lunghezza.
L'unità di misura di H che deriva ovviamente dallo stesso teorema di Ampere che definisce H, è l'Ampere su metro [H]=[A][M]-1
Riflettiamo ora su quanto ottenuto. L'intensità di corrente elettrica genera il campo magnetico. Ogni punto dello spazio è caratterizzato da un vettore che abbiamo chiamato campo magnetico le cui caratteristiche sono determinate dall'intensità di corrente e dal suo numero di rotazioni complete e dalla lunghezza della linea di forza. Si è dunque definita un'entità legata alla causa del campo. Nulla è stato detto circa gli effetti prodotti: ad esempio, quali sono e se dipendono dal mezzo materiale in cui si sviluppa il campo? Possiamo con una certa sicurezza pensare che dipendono da H e, probabilmente anche dal mezzo, ma come tenerne conto?
Un problema simile si è già presentato affrontando lo studio della stessa corrente elettrica e molti altri sono i fenomeni fisici analoghi cui potremmo riferirci. Ma ripensiamo alla corrente nei conduttori. Le cariche libere possono assumere un movimento comune se sono soggette ad un campo elettrico che viene generato da una separazione di cariche quantificata in generale come differenza di potenziale.Il campo elettrico è legato dunque alla separazione di carica come il campo magnetico è legato alle cariche in moto. Il campo elettrico nei conduttori dà origine ad un movimento di cariche libere tanto più intenso quanto più intenso è il campo e dipendente dal tipo di conduttore in cui il campo è impresso. In pratica si può dire che la densità di corrente (effetto) è proporzionale al campo elettrico e la costante di proporzionalità è una caratteristica del mezzo materiale che chiamiamo conduttività.
Sinteticamente
J=gK
J è la densità di corrente [A][M]-2 e K il campo elettrico [V][M]-1 L'unità di misura di g è [W]-1[M]-1
Per riconoscere quali sono gli effetti prodotti da un campo magnetico possiamo far riferimento alla struttura fondamentale mostrata nel disegno, che chiameremo Principio del generatore.

Un conduttore giacente sul piano del disegno, è immerso, per la lunghezza l, in un campo magnetico le cui linee di forza sono perpendicolari al piano nel disegno con verso entrante (x).
Se si sposta il conduttore trasversalmente, con una velocità costante perpendicolare alla sua lunghezza ed alle linee di forza magnetiche, si può rilevare ai suoi capi una differenza di potenziale, la f.e.m. indotta E, proporzionale al prodotto della lunghezza del conduttore per la velocità. La costante di proporzionalità è una proprietà del campo magnetico e del mezzo nel quale esso si sviluppa. Viene indicata con B e chiamata induzione magnetica.
Per quanto riguarda il verso della f.e.m. E si può ricorrere alla regola della mano destra (la freccia in corrispondenza di E indica il +)
:
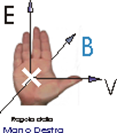Si ha
E=Blv
Dall'analisi dimensionale vediamo che l'unità di misura di B, denominata Tesla vale
[T]=[V][s][M]-2
La grandezza fisica avente le dimensioni di un impulso di tensione [V][s], detto weber [Wb], viene chiamata flusso magnetico ed indicata con F. L'induzione B appare allora come un flusso magnetico per unità di superficie, o specifico e, se è possibile paragonare il flusso magnetico al flusso di cariche elettriche o corrente elettriche allora B può essere paragonato alla densità di corrente. Il flusso è una entità matematica definita nei campi vettoriali è lo si può graficamente immaginare come l'insieme di linee di forza che attraversano una superficie.
Il disegno successivo mostra invece l'altro effetto che chiameremo Principio del motore.

Se nel conduttore è impressa una corrente di intensità I esso risente di una forza trasversale perpendicolare alla sua lunghezza ed alle linee del campo e si ha che l'intensità di questa forza è proporzionale al prodotto l*I. La costante di proporzionalità è identica a quella trovata in precedenza per cui viene indicata ancora con B.
Per quanto riguarda il verso della Forza si può ricorrere alla regola della mano sinistra:

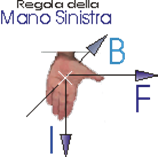
Si ha
F=BlI

Dall'analisi dimensionale vediamo che
[T]=[N][s][M]-1[C]-1
identica a quella precedente essendo [N][C]-1=[V][M]-1
Possiamo allora riconoscere come effetto magnetico proprio B e, constatando con esperimenti successivi che a parità di H, B dipende dal mezzo, porre
B=mH
dove m m è denominata permeabilità magnetica assoluta del mezzo. L'unità di misura la ricaviamo dall'analisi dimensionale
[T][A]-1[M]=[V][s][M]-2[A]-1M]=[W][s][M]-1=[H][A]-1
avendo posto [H]=[W][s] ][s] unità di misura,
Se il mezzo è il vuoto la permeabilità assoluta vale
m0= 4p10-7 H/m
Si definisce costante dielettrica relativa il numero puro dato dal rapporto tra la permeabiltà assoluta del mezzo e la permeabilità assoluta del vuoto.
mr=m/m0

Fonte: http://vgg.labcad.di.unimi.it/cbus/webscu/2005/Istituto_Maria_Consolatrice/_private/Contenuti/Fisica/Fenomeni%20magnetici.doc

Sito web da visitare: http://vgg.labcad.di.unimi.it/cbus

Autore del testo: non indicato nel documento di origine

Nota : se siete l'autore del testo sopra indicato inviateci un e-mail con i vostri dati , dopo le opportune verifiche inseriremo i vostri dati o in base alla vostra eventuale richiesta rimuoveremo il testo.

Fenomeni magnetici