Dispensa di fisica

I riassunti, le citazioni e i testi contenuti in questa pagina sono utilizzati per sole finalità illustrative didattiche e scientifiche e vengono forniti gratuitamente agli utenti.

DISPENSE DI FISICA

Cinematica

Traiettoria e legge oraria

La meccanica si divide in tre grandi settori: la statica che studia l'equilibrio dei corpi, la cinematica che studia il moto dei corpi senza indagarne le cause e la dinamica che studia il moto e le sue cause. In questa sezione cominceremo lo studio della cinematica, limitandoci al movimento di punti materiali. Un corpo si può considerare con buona approssimazione un punto materiale se le sue dimensioni sono piccole rispetto alle dimensioni della regione di spazio in cui avviene il moto.

È importante chiarire fin dall'inizio che il moto in fisica è un concetto relativo. Supponiamo di essere su un treno in prossimità di una stazione ferroviaria. Fuori dal finestrino vediamo un altro treno e notiamo che si sta muovendo rispetto a noi. È impossibile da questa sola osservazione stabilire quale dei due treni si sta muovendo rispetto alla stazione. Voi che state leggendo queste pagine siete fermi rispetto alla stanza nella quale vi trovate ma nello stesso tempo la Terra vi sta trasportando a una velocità di oltre 100mila chilometri all'ora attorno al Sole.

In genere è importante stabilire un sistema di riferimento rispetto al quale descrivere il moto: ad esempio nel caso del moto di un treno i binari costituiscono un buon sistema di riferimento e la stazione ferroviaria può essere considerata come l'origine di tale sistema di riferimento. In generale il sistema di riferimento è una retta se il moto avviene lungo una retta, è un piano cartesiano se il moto avviene su un piano, è tridimensionale se il movimento avviene nello spazio.
Una volta stabilito il sistema di riferimento, per poter descrivere un moto bisogna stabilire qual è l'insieme delle posizioni che vengono assunte dal corpo in movimento. Tale insieme prende il nome di traiettoria. Ad esempio, la traiettoria di un corpo in caduta libera è una retta verticale, la traiettoria di un proiettile sparato orizzontalmente da un cannone è una curva che prende il nome di parabola. In questi esempi la traiettoria è un grafico nello spazio, che unisce fra loro tutte le posizioni occupate dal corpo, man mano che il tempo passa.

La scelta del sistema di riferimento e la traiettoria non sono sufficienti per descrivere in maniera univoca il moto di un corpo. La stessa traiettoria infatti può essere percorsa in molti modi diversi, ad esempio un treno può percorrere lo stesso binario rettilineo a diverse velocità. In altre parole, la traiettoria da sola non è sufficiente per stabilire dove si trova un corpo ad un certo istante di tempo. È importante specificare anche qual è la legge oraria del moto. La legge oraria è una relazione matematica che lega tra loro il tempo t e la posizione s occupata dal corpo in quell'istante di tempo. Se il moto avviene in una sola dimensione, ad esempio lungo una retta, il grafico della legge oraria è una linea in un piano cartesiano avente lo spazio s in ordinata e il tempo t in ascissa. Come abbiamo già detto in precedenza, alla stessa traiettoria possono corrispondere leggi orarie diverse, a conferma del fatto che traiettoria e legge oraria sono due concetti totalmente indipendenti.

Velocità

Nella precedente sezione abbiamo detto che la stessa traiettoria può corrispondere a leggi orarie diverse, in particolare la stessa traiettoria può essere percorsa a velocità diverse. In generale la conoscenza della legge oraria consente il calcolo della velocità di un corpo. Infatti se conosciamo dove si trova il corpo ad ogni istante di tempo conosciamo anche quanto spazio ha percorso in un certo intervallo di tempo. La velocità media v di un corpo si definisce come il rapporto tra lo spazio Δs percorso in un certo intervallo di tempo e l'intervallo di tempo Δt impiegato a percorrerlo: v = Δs / Δt. Se conosciamo il punto iniziale s1 in cui si trova il corpo nell'istante iniziale t1 e il punto finale s2 in cui si trova il corpo all'istante t2 possiamo riscrivere Δs = s2 - s1 e Δt = t2 - t1, da cui la formula per la velocità media diventa vm = (s2 - s1) / (t2 - t1). L'unità di misura della velocità nel Sistema Internazionale è il metro al secondo (m / s).

Accelerazione

In generale la velocità di un corpo non rimane costante nel tempo ma può aumentare o diminuire. Una grandezza fisica importante per descrivere il moto di un corpo è l'accelerazione media, la quale viene definita come il rapporto tra la variazione di velocità e l'intervallo di tempo in cui tale variazione avviene: am = (v2 - v1) / (t2 - t1). Dal momento che l'unità di misura della velocità nel Sistema Internazionale è il metro al secondo (m / s), l'unità di misura dell'accelerazione è il metro al secondo quadro (m / s2). Come nel caso della velocità anche qui possiamo introdurre il concetto di accelerazione istantanea: l'accelerazione media diventa uguale all'accelerazione istantanea quando rendiamo molto piccolo l'intervallo di tempo t2 - t1. L'accelerazione media in un intervallo molto piccolo di tempo coincide con l'accelerazione del corpo in quell'istante di tempo.

Esempi di moto

Moto rettilineo uniforme

Dopo aver introdotto i concetti fondamentali che servono a studiare la cinematica, ossia traiettoria e legge oraria, velocità e accelerazione, andremo ora a studiare alcuni esempi particolari di moto. Il primo esempio di moto che consideriamo è il moto rettilineo uniforme, ossia un moto che avviene su una traiettoria rettilinea con velocità costante. Dal momento che la velocità di un corpo v è definita come v = Δs / Δt, se v è costante anche il rapporto Δs / Δt è costante. Questo vuol dire che lo spazio percorso Δs e l'intervallo di tempo impiegato a percorrerlo Δt sono direttamente proporzionali.
Dalla definizione stessa di velocità possiamo ricavarci la legge oraria del moto rettilineo uniforme. Per prima cosa, invertendo la formula che definisce la velocità, otteniamo: Δs = v · Δt, con v costante. Tale relazione può essere riscritta come s - s0 = v · (t - t0), dove s0 è la posizione occupata dal corpo all'istante iniziale t0, mentre s è la posizione occupata dal corpo all'istante di tempo generico t. Come caso particolare, consideriamo il caso in cui l'istante iniziale t0 coincide con il momento in cui facciamo partire il cronometro. Allora possiamo porre t0 = 0 e otteniamo: s - s0 = v · t. Sommando s0 ad entrambi i membri otteniamo finalmente la legge oraria del moto rettilineo uniforme: s = v · t + s0. Tale relazione ci dice che, per conoscere la posizione del corpo s ad ogni istante di tempo t, dobbiamo conoscere la posizione iniziale del corpo s0 e la sua velocità v. Ad esempio se all'istante iniziale il corpo si trova a s0 = 20 m dall'origine del sistema di riferimento e mantiene una velocità costante di v = 10 m / s, avremo che dopo un tempo t = 30 s il corpo si troverà a s = 10 m / s · 30 s + 20 m = 320 m dall'origine del sistema di riferimento.

Moto rettilineo uniformemente accelerato

Un altro esempio molto importante di moto è il moto rettilineo uniformemente accelerato, caratterizzato da una traiettoria rettilinea e da un'accelerazione costante. Questo significa che in un moto rettilineo uniformemente accelerato l'accelerazione a non varia nel tempo. Se ora ci ricordiamo com'è definita l'accelerazione, a = (v - v0) / (t - t0), possiamo dire che in un moto rettilineo uniformemente accelerato il rapporto tra la variazione di velocità v - v0 e l'intervallo di tempo t - t0 è uguale a una costante. Questo vuol dire che la variazione di velocità e l'intervallo di tempo in cui tale variazione avviene sono direttamente proporzionali: v - v0 = a · (t - t0).

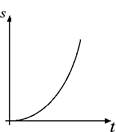Come caso particolare, supponiamo di far partire il cronometro all'istante t0 = 0 e che in quell'istante il corpo risulti fermo v0 = 0. In questo caso la velocità del corpo v e il tempo t risultano direttamente proporzionali: v = a · t e il grafico è la retta passante per l'origine riportata in figura:
Andiamo ora a ricavarci la legge oraria del moto rettilineo uniformemente accelerato. Come abbiamo detto nella precedente sezione lo spazio s percorso dal corpo è dato dall'area del triangolo che ha per base il tempo t e per altezza la velocità v raggiunta dal corpo all'istante t. Ricordandoci ora che v = a · t, la legge oraria del moto uniformemente accelerato diventa s = 1/2 · v · t = 1/2 · a · t2. Se nel moto rettilineo uniforme lo spazio percorso è direttamente proporzionale al tempo t, nel moto rettilineo uniformemente accelerato lo spazio è direttamente proporzionale al quadrato del tempo.

Forze ed Equilibrio

LE FORZE

Definizione operativa

Una forza rappresenta una grandezza fisica vettoriale, la cui intensità è misurata con uno strumento chiamato dinamometro.
L’unità di misura delle forze è il Newton (N) che rappresenta una unità derivata (N = kg·(m/s2))
La forza è un vettore perché oltre all’intensità è necessario specificare anche direzione e verso.

La forza peso
Sulla Terra, ogni corpo subisce una forza-peso, che è la forza di gravità con cui è attratto dalla Terra, quindi questo tipo di forza agisce a distanza.
La forza-peso e la massa sono grandezze diverse:

la forza-peso è un vettore, la cui intensità è misurata con il dinamometro, mentre la direzione è quella verticale e il verso rivolto in direzione del centro della Terra.
la massa è uno scalare ed esprime la quantità di materia di cui è costituito un corpo, si misura con una bilancia a piatti uguali

mentre la massa non cambia mai qualsiasi parte dell’universo noi andiamo, la forza-peso invece cambia.

Come è facilmente dimostrabile, in un dato luogo, la forza-peso di un corpo è direttamente proporzionale alla sua massa. Il fattore di proporzionalità è chiamato accelerazione di gravità e si indica con il simbolo g , tale valore cambia da punto a punto sulla Terra, in particolare al livello del mare vale circa 9,8 N/kg

FP=g·m

Equilibrio per traslazioni

Condizione di equilibrio

In questa sezione vogliamo cominciare a studiare la statica, ossia quella parte della meccanica che si occupa dell'equilibrio dei corpi. Partiremo con lo studio dell'equilibrio dei corpi per traslazioni. Un corpo subisce una traslazione quando ogni suo punto si sposta della stessa quantità nella stessa direzione e nello stesso verso, in altre parole quando ogni suo punto è sottoposto allo stesso vettore spostamento.

In fisica giocano un ruolo importante i cosiddetti corpi rigidi. Un corpo rigido è un corpo che non si può deformare, ossia un corpo in cui ogni punto mantiene nel tempo la stessa distanza da ogni altro punto del corpo. In generale studiare il moto o l'equilibrio di un corpo rigido può non essere banale se il corpo rigido non ha forma regolare. Se però il corpo rigido ha forma regolare (ad esempio sferica) si può immaginare tutta la massa del corpo concentrata in un punto che è il centro di simmetria del corpo (nell'esempio della sfera, il suo centro). Questo centro di simmetria va anche sotto il nome di baricentro.

Lo studio del moto oppure dell'equilibrio del corpo rigido viene in questo modo ridotto allo studio del moto oppure dell'equilibrio di un particolare punto dotato di massa, ossia di un particolare punto materiale. In queste lezioni useremo sempre per semplicità questo modello del punto materiale, ossia immagineremo tutta la massa M del corpo rigido concentrata nel baricentro che pertanto risulterà sottoposto a una forza-peso totale pari a M · g, dove g = 9.8 N / kg. Più in generale, si può utilizzare il modello del punto materiale quando il corpo è molto più piccolo delle dimensioni fisiche che caratterizzano il problema e quando le direzioni di tutte le forze agenti sul corpo si incontrano in un unico punto.

Anche nel linguaggio di tutti i giorni diciamo che un corpo è in equilibrio quando non si muove. Cerchiamo ora di tradurre questa definizione a parole di equilibrio in formule matematiche, limitandoci per il momento alle traslazioni. Abbiamo visto che le forze hanno effetti dinamici, ossia sono in grado di mettere in movimento i corpi ai quali sono applicate. Per avere equilibrio per traslazioni è perciò necessario che la somma vettoriale di tutte le forze applicate al corpo in esame sia uguale a 0:

Ad esempio consideriamo due squadre che giocano a tiro alla fune: se una squadra applica una forza diretta orizzontalmente da destra a sinistra di intensità F e la squadra avversaria applica una forza di ugual intensità F, ma diretta orizzontalmente da sinistra a destra, avremo che la somma dei due vettori forza, uguali ed opposti, è uguale a zero e la fune risulta perciò in equilibrio.
Se ragioniamo in termini di componenti dei vettori avremo che, per avere equilibrio, la somma di tutte le componenti orizzontali dei vettori forza deve essere uguale a zero, così come deve essere uguale a zero la somma di tutte le componenti verticali dei vettori forza. Vedremo nelle prossime sezioni varie applicazioni di questo concetto.

Forza equilibrante, reazione vincolare

Abbiamo visto nella sezione precedente che la condizione di equilibrio per traslazioni è l'annullamento della forza totale (detta anche risultante) applicata al corpo. Vediamo quali conseguenze ha questa condizione di equilibrio. Supponiamo che ci sia una forza che agisce su un corpo. Evidentemente il corpo non è in equilibrio. Come facciamo a ripristinare la condizione di equilibrio? Possiamo aggiungere una seconda forza uguale ed opposta alla prima, ossia una forza con ugual direzione, uguale intensità ma verso opposto. Una forza con queste caratteristiche è detta forza equilibrante.

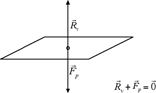Un esempio in cui entra in gioco la forza equilibrante è quello di un corpo posto su un tavolo. Sappiamo che ogni corpo dotato di massa è soggetto a una forza-peso. Perché allora il corpo risulta essere in equilibrio? Evidentemente perché esiste una forza in grado di equilibrare la forza-peso del corpo: il tavolo, con la sua presenza, esercita una forza sul corpo uguale ed opposta alla forza-peso. Questa particolare forza equilibrante prende il nome di reazione vincolare del piano:

Ovviamente la forza peso di un corpo può essere equilibrata anche per mezzo di più forze, come nel caso dell'insegna in figura tenuta in equilibrio grazie alla tensione esercitata da due fili:

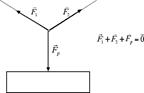Usando la regola del parallelogramma è facile verificare graficamente che la somma vettoriale delle due tensioni esercitate dai fili obliqui è esattamente uguale alla forza-peso dell'insegna. In questo modo la risultante di tutte le forze è uguale a zero e l'insegna risulta in equilibrio.

Equilibrio per rotazioni

Momento di una forza

Per introdurre il concetto di momento di una forza partiamo dalla seguente domanda: perché nelle porte le maniglie sono sempre dalla parte opposta rispetto ai cardini? Supponiamo di voler aprire un vecchio portone poco oliato. Dalla nostra esperienza sappiamo che si fa meno fatica (in altre parole, è sufficiente applicare una forza minore) spingendo il portone dalla parte opposta rispetto ai cardini. Altro esempio che ci può aiutare è quello della chiave inglese e del bullone. Anche in questo caso è molto più facile ruotare il bullone applicando la forza all'estremità del manico della chiave inglese, ossia nel punto più lontano rispetto al punto attorno al quale avviene la rotazione. Da tutti questi esempi ricaviamo che, in presenza di un corpo che può ruotare, gli effetti di una forza applicata al corpo dipendono da tre fattori:

l'intensità della forza: se applichiamo una forza maggiore, la rotazione del bullone o del portone risulta essere agevolata;
il punto di applicazione della forza: a parità di intensità la rotazione è notevolmente agevolata se applichiamo la forza nel punto più lontano dal centro di rotazione;
la direzione della forza: se applichiamo una forza diretta lungo il manico della chiave inglese non si verifica alcuna rotazione.

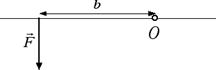
Nella figura riportata sopra O è il punto attorno al quale avviene la rotazione (ad esempio il centro del bullone), b è la distanza tra la retta d'azione della forza e il punto attorno al quale avviene la rotazione. Questa distanza prende anche il nome di braccio della forza. Il momento di una forza M si definisce come il prodotto dell'intensità F della forza per la lunghezza b del braccio: M = F · b. Dal momento che nel Sistema Internazionale la forza si misura in newton e il braccio in metri l'unità di misura del momento della forza è il newton per metro (N · m). Ad esempio, se l'intensità della forza è F = 5 N e il braccio misura b = 6 cm avremo un momento della forza pari a M = 5 N · 0.06 m = 0.3 N · m. Come casi particolari, se la retta d'azione della forza passa per il centro di rotazione O abbiamo che b = 0. In questo caso il momento della forza si annulla e non si verifica alcuna rotazione.

Il momento di una forza è la grandezza che regola i movimenti di rotazione. A questo punto è chiaro che possiamo aumentare il momento M sia aumentando l'intensità della forza F sia aumentando il braccio b: questo è il motivo per cui il portone si apre più facilmente se lo spingiamo dalla parte opposta rispetto ai cardini o per cui il bullone si allenta più facilmente spingendo una chiave inglese all'estremità del manico. Per convenzione si associa un segno alle rotazioni: il momento di una forza è un numero positivo se le rotazioni che esso provoca sono antiorarie, è invece un numero negativo se le rotazioni che esso induce sono orarie. Questa convenzione sarà di fondamentale importanza nella prossima sezione, dove andremo a stabilire quali sono le condizioni di equilibrio di un corpo che può ruotare.

Condizione di equilibrio

Abbiamo visto che, nel caso dei moti di traslazione, la condizione di equilibrio è data dall'annullarsi della risultante delle forze applicate al corpo. Vogliamo ora chiarire qual è la condizione di equilibrio per un corpo che è libero di ruotare. Abbiamo visto nella precedente sezione che il momento di una forza assume segni positivi o negativi a seconda del senso in cui avviene la rotazione. La condizione di equilibrio per rotazioni è data dall'annullarsi della somma di tutti i momenti che vengono applicati al corpo, ossia: Mtot = M1 + M2 + M3 + ... = 0. Se prescindiamo dai segni, possiamo anche dire che un corpo non ruota quando la somma di tutti i momenti orari applicati al corpo è uguale alla somma di tutti i momenti antiorari. Questa è la condizione di equilibrio per rotazioni.

Leggi della dinamica

Primo principio della dinamica

Galileo enunciò il primo principio della dinamica: Un corpo persevera nel suo stato di quiete o moto rettilineo uniforme, a meno che non intervenga una causa esterna a modificarne lo stato. Il primo principio della dinamica è anche detto principio d'inerzia. L'inerzia è la proprietà che un corpo possiede di opporsi al cambiamento del suo stato di moto: è tanto maggiore quanto maggiore è la massa del corpo.
Da quanto abbiamo appena visto, il primo principio della dinamica ci dice che, quando nessuna forza agisce su un corpo, il corpo mantiene la sua velocità: se il corpo è fermo rimane fermo, se si muove a una certa velocità continua a muoversi con la stessa velocità. Nella realtà gli esperimenti ideali di Galileo sono difficili da realizzare a causa delle forze d'attrito. Esistono però certi dispositivi, come il ghiaccio secco o la rotaia a cuscino d'aria, tramite i quali è possibile ridurre al massimo gli attriti e riprodurre con buona approssimazione gli esperimenti ideali di Galileo.

Secondo principio della dinamica

Nella precedente sezione abbiamo visto che, se nessuna forza agisce su un corpo, tale corpo mantiene invariata la sua velocità. Cosa succede invece quando applichiamo una forza costante ad un corpo? Una forza costante F produce un'accelerazione costante a. In particolare, forza ed accelerazione sono direttamente proporzionali e la costante di proporzionalità coincide con la massa m del corpo. Possiamo pertanto scrivere che F = m · a.
Non dobbiamo però dimenticarci che sia la forza che l'accelerazione sono due grandezze vettoriali. Il secondo principio della dinamica ci dice che la forza e l'accelerazione hanno la stessa direzione e lo stesso verso. In termini vettoriali possiamo perciò scrivere il secondo principio della dinamica come: . La grandezza fisica m è detta massa inerziale ed è una misura dell'inerzia del corpo.

Terzo principio della dinamica

Il terzo principio della dinamica afferma che se un corpo A esercita su un corpo B una certa forza . Tale principio è detto anche principio di azione e reazione: ad ogni azione corrisponde un azione uguale e contraria.

Temperatura e dilatazione termica

Scale termometriche

La materia è formata da molecole ognuna delle quali ha una sua velocità e, di conseguenza, una sua energia cinetica. Tanto maggiore è l'energia cinetica di queste molecole, tanto maggiore è la temperatura. Infatti la temperatura di un corpo è un indice dell'agitazione termica, ossia dell'energia cinetica delle molecole che compongono il corpo. Per renderci conto di ciò è sufficiente accendere un fuoco e osservare le molecole d'aria presenti nei dintorni: ci accorgiamo subito che l'aumento di temperatura nei pressi del fuoco comporta un aumento della velocità delle molecole.

La misura della temperatura, che è una grandezza fisica fondamentale nel Sistema Internazionale, si basa su due fenomeni fisici distinti che andremo ad analizzare in dettaglio: l'equilibrio termico e la dilatazione termica. Cominciamo a studiare l'equilibrio termico: quando poniamo a contatto due corpi aventi temperatura diversa, le molecole di questi due corpi subiscono continui urti e in questi urti il corpo più caldo cede energia cinetica al corpo più freddo finché le molecole dei due corpi vengono ad avere in media la stessa energia cinetica. A livello macroscopico questo si riflette nel fatto che i due corpi vengono ad avere la stessa temperatura.
L'altro fenomeno su cui si basa la misura della temperatura è la dilatazione termica, ossia l'effetto per il quale quando scaldiamo un corpo, esso si dilata. Su questi due principi fisici si basa il termometro clinico. Infatti quando poniamo il termometro clinico a contatto con la nostra pelle, cediamo parte del nostro calore al termometro finché si arriva a una temperatura di equilibrio (che praticamente coincide con quella del nostro corpo). Il mercurio presente all'interno del termometro clinico si dilata a causa dell'aumento di temperatura e dalla dilatazione termica del mercurio possiamo risalire alla temperatura del nostro corpo.

Per tarare un termometro è importante fissare delle temperature di riferimento. Queste temperature sono: 0°C (temperatura di fusione del ghiaccio a pressione atmosferica) e 100°C (temperatura di evaporazione dell'acqua). Questo intervallo di 100°C viene poi diviso in 100 parti uguali per definire il grado Celsius (°C), detto anche grado centigrado. Questa prima scala di temperatura, che è quella che usiamo quotidianamente, prende il nome di scala centigrada o scala Celsius.
Esistono altre scale di temperatura, a cominciare dalla temperatura assoluta, che si misura in gradi Kelvin (K). È anch'essa una scala centigrada ma tutte le temperature risultano traslate rispetto alla scala Celsius. In generale, se indichiamo con TC la temperatura del corpo in gradi Celsius e con TK la temperatura dello stesso corpo in gradi Kelvin vale la seguente relazione TK = TC + 273.15. In particolare, la temperatura 0 K = -273.15°C corrisponde al cosiddetto zero assoluto. Questa è una temperatura limite: è infatti impossibile scendere al di sotto dello zero assoluto. Questa temperatura corrisponde infatti a energia cinetica nulla da parte di tutte le molecole. Nella pratica, è molto difficile raggiungere lo zero assoluto anche se con le moderne tecniche si sono raggiunte temperature dell'ordine del µK (10-6 K). Le temperature più alte presenti in natura si raggiungono invece nel centro delle stelle: ad esempio, all'interno del Sole si raggiungono i 3 milioni di gradi Kelvin.
Una terza scala termometrica è utilizzata nei paesi anglosassoni e prende il nome di scala Fahrenheit. In tale scala la temperatura di fusione del ghiaccio, 0°C, corrisponde a 32°F mentre la temperatura di ebollizione dell'acqua, 100°C, corrisponde a 212°F. È chiaro già da questa corrispondenza che la scala Fahrenheit non è una scala centigrada.

Dilatazione lineare

Come abbiamo detto nella precedente sezione, uno dei principi fisici su cui si basa la misura della temperatura con un termometro clinico è la dilatazione termica che in questa sezione andremo ad analizzare un po' più in dettaglio. Quando vengono riscaldati i corpi si dilatano. Consideriamo ad esempio un'asta di lunghezza l0 a una temperatura iniziale T0. Portiamo l'asta a una temperatura finale T in modo tale che la variazione di temperatura sia uguale a ΔT = T - T0. L'asta si allungherà di una quantità pari a Δl, come indicato nella figura seguente:
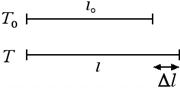Sperimentalmente si verifica che l'allungamento Δl è direttamente proporzionale alla lunghezza iniziale dell'asta l0 e alla variazione della temperatura ΔT, ossia Δl = λ l0 ΔT. Il coefficiente di proporzionalità λ prende il nome di coefficiente di dilatazione lineare. Dal momento che λ = Δl / (l0 · ΔT) avremo che il coefficiente di dilatazione lineare si misura in °C-1 oppure in K-1.
Il coefficiente di dilatazione lineare dipende dalla sostanza che prendiamo in esame. Nella tabella seguente riportiamo i valori di λ per alcune sostanze:

Sostanza	Piombo	Alluminio	Ferro	Acciaio
λ (°C-1)	2.9·10-5	2.4·10-5	1.2·10-5	1.2·10-5

Dilatazione volumica

Un discorso analogo a quello che abbiamo visto nella precedente sezione vale se abbiamo a che fare con dei solidi tridimensionali anziché con delle aste. Supponiamo per semplicità di considerare un cubo di lato iniziale l0 e, di conseguenza, di volume iniziale V0 = (l0)3. Supponiamo anche di andare ad aumentare la temperatura da T0 a T0 + ΔT. Ognuno dei lati del cubo subirà una dilatazione lineare, ossia la lunghezza finale del lato sarà l = l0 + Δl. Andiamo a calcolarci il volume finale del cubo:
V = l3 = (l0 + Δl)3 = (l0)3 + 3 · (l0)2 · Δl + 3 · l0 · (Δl)2 + (Δl)3.
Ora la dilatazione termica Δl è in genere un numero piccolo, pertanto nella precedente espressione, quando eleviamo al quadrato o al cubo Δl otterremo degli addendi trascurabili rispetto agli altri termini. Pertanto, ricordandoci anche che Δl = λ · l0 · ΔT, possiamo approssimare il volume del cubo come segue:
V ≈ (l0)3 + 3 · (l0)2 · λ · l0 · ΔT = (l0)3 + 3 · λ · (l0)3 · ΔT = V0 + 3 · λ · V0 · ΔT.
In definitiva, la variazione di volume dovuta alla dilatazione termica è ΔV = k · V0 · ΔT, dove k = 3 · λ è il cosiddetto coefficiente di dilatazione volumica. Come conseguenza del fatto che la dilatazione di un cubo o di un qualunque solido tridimensionale può avvenire lungo tre distinte direzioni abbiamo che il coefficiente di dilatazione volumica è il triplo del coefficiente di dilatazione lineare.

Termologia

Calore specifico

Legge fondamentale della termologia

Ci sono diversi modi per aumentare la temperatura di una sostanza liquida, come ad esempio l'acqua: ponendo la sostanza a diretto contatto con una fiamma, agitando l'acqua, esponendo l'acqua ai raggi del sole oppure facendo passare corrente nell'acqua. Un'esperienza fondamentale al riguardo è quella del mulinello di Joule schematizzato nella figura che segue:

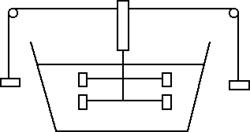L'energia potenziale dei pesi si converte progressivamente in energia cinetica di rotazione del cilindro e delle pale ad esso collegate. Tali pale agitano l'acqua contenuta nel recipiente. Alla fine, quando i pesi giungono a terra, il sistema progressivamente si ferma e, se si misura la temperatura dell'acqua, si scopre che è aumentata. Di quanto? Supponiamo che ΔE sia la perdita di energia meccanica del sistema (coincidente con l'energia potenziale gravitazionale iniziale dei pesi). Indichiamo invece con ΔT l'aumento di temperatura dell'acqua. Quello che si scopre è che il rapporto tra la variazione di energia ΔE e la variazione di temperatura ΔT è uguale a una costante C, detta capacità termica dell'acqua.
La capacità termica è una caratteristica della sostanza che stiamo considerando ma dipende anche dalla massa m della sostanza. È abbastanza intuitivo infatti che, a parità di energia fornita, riusciamo a riscaldare molto più facilmente un corpo che ha una piccola massa (nella fattispecie una piccola quantità di acqua). Infatti la capacità termica C può essere riscritta come C = c · m, dove c è una costante che dipende dalla sostanza in esame e prende il nome di calore specifico, m è invece la massa della sostanza. In definitiva possiamo riscrivere la variazione di energia meccanica dei pesi ΔE come ΔE = c · m · ΔT. Vale la pena menzionare fin da subito il valore del calore specifico dell'acqua che useremo spesso negli esercizi: c = 4186 J / (kg · K). Questo significa che sono necessari 4186 J di energia per alzare di 1 grado Kelvin la temperatura di 1 kg di acqua. Questo valore elevato rende l'acqua uno stabilizzatore termico: i terreni ricchi di acqua, i mari o i laghi si riscaldano molto di meno rispetto ai terreni aridi o ai deserti.

L'energia meccanica dei pesi non viene dunque persa ma viene acquistata sotto forma di calore dall'acqua. Il calore acquistato o ceduto da una sostanza che aumenta la sua temperatura di ΔT è uguale a

Q = c · m · ΔT.

Questa relazione prende il nome di legge fondamentale della termologia.

Poiché il calore ceduto determina un aumento della temperatura, ossia, a livello microscopico, un aumento dell'energia cinetica delle molecole, possiamo concludere che il calore è una forma di energia, detta anche energia termica. Se teniamo in considerazione questo fatto, possiamo dire che quella che si conserva non è l'energia meccanica ma la somma di energia meccanica ed energia termica. Quando ci sono degli attriti sappiamo che l'energia meccanica non si conserva. Ora abbiamo scoperto qual è la ragione: in presenza di attriti parte dell'energia meccanica viene convertita in energia termica, ossia in calore.
Per concludere questa sezione, vogliamo menzionare come un'altra unità di misura molto usata per il calore sia la caloria: una caloria è la quantità di calore necessaria per portare 1 g d'acqua dalla temperatura di 14.5°C alla temperatura di 15.5°C. È facile rendersi conto che le definizioni di caloria e di calore specifico dell'acqua implicano la seguente equivalenza: 1 cal = 4.186 J. Se usiamo la caloria come unità di misura del calore, il calore specifico verrà ad essere misurato in cal / (g°C).

Trasferimenti di energia

Cambiamenti di stato

Calore latente di fusione

Lo scopo principale di questa sezione è quello di provare come il calore ceduto a un corpo non sempre implichi un aumento di temperatura. L'eccezione è costituita dai cambiamenti di stato. Quando noi forniamo calore a un blocco di ghiaccio, la temperatura del ghiaccio aumenta fino ad arrivare a 0°C. Se forniamo ulteriore calore notiamo che la temperatura del ghiaccio non aumenta ma rimane costante. In questa fase infatti il calore fornito serve per far fondere il ghiaccio.
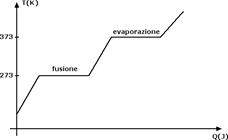Quando tutto il ghiaccio è fuso, il calore che forniamo all'acqua serve di nuovo per aumentare la sua temperatura finché arriviamo a una temperatura di 100°C. A quel punto il calore ulteriore che cediamo serve al nuovo cambiamento di stato, da liquido a gas. In questa fase di nuovo la temperatura rimane costante finché tutta l'acqua non è evaporata. L'andamento della temperatura T in funzione del calore Q è riportato nel seguente grafico:
Dopo questa introduzione qualitativa cerchiamo di capire quanto calore serve per far fondere una massa m di ghiaccio o di una qualunque sostanza allo stato solido. È abbastanza intuitivo che questo calore risulta tanto maggiore quanto maggiore è la massa m di sostanza da fondere. In particolare, il calore di fusione Q e la massa m sono direttamente proporzionali Q = λf · m. Il coefficiente di proporzionalità prende il nome di calore latente di fusione e dipende dalla sostanza che prendiamo in esame. Dal momento che λf = Q / m la sua unità di misura nel Sistema Internazionale è il J / kg. Nel caso particolare dell'acqua abbiamo che λf = 3.34 · 105 J / kg. Questo significa che, a pressione atmosferica, per fondere 1 kg di ghiaccio servono 3.34 · 105 J.

È importante precisare a pressione atmosferica perché, se cambiamo la pressione, le grandezze fisiche che caratterizzano il cambiamento di stato cambiano. Ad esempio, se aumentiamo la pressione sul ghiaccio possiamo abbassare la temperatura di fusione al di sotto degli 0°C. Ci si può rendere conto di ciò mantenendo a qualche grado sotto lo zero un blocco di ghiaccio. Appoggiando sopra tale blocco un filo dotato alle sue estremità di due pesi, abbiamo che la pressione esercitata dal filo sul ghiaccio abbassa la temperatura di fusione e il ghiaccio sotto il filo comincia a fondere. Il filo riesce a penetrare nel blocco di ghiaccio mentre al di sopra del filo la pressione torna ad essere quella atmosferica e si ricrea il blocco di ghiaccio visto che siamo a una temperatura inferiore a 0°C. In questo modo il filo riesce ad attraversare completamente il blocco di ghiaccio!

Calore latente di evaporazione

Abbiamo visto nella precedente sezione che i cambiamenti di stato avvengono a temperatura costante ma con scambio di calore. Di seguito riportiamo i nomi e le temperature che caratterizzano i cambiamenti di stato dell'acqua.

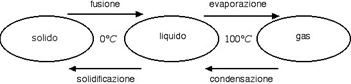
In alcuni casi (es.: naftalina) è possibile far avvenire il cambiamento di stato da solido a gas senza passare attraverso la fase liquida. Questo processo prende il nome di sublimazione. Il passaggio opposto da gas a solido prende invece il nome di brinamento, dal momento che la brina ne è un tipico esempio.
Il calore latente di evaporazione dipende dalla sostanza che prendiamo in considerazione. Come il calore latente di fusione, anche il calore latente di evaporazione è direttamente proporzionale alla massa m, ossia Q = λv · m. Il coefficiente di proporzionalità λv dipende dalla sostanza che prendiamo in considerazione. Nel caso dell'acqua a pressione atmosferica λv = 2.25 · 106 J / kg. Questo vuol dire che serve una quantità di calore pari a Q = 2.25 · 106 J per far evaporare 1 kg di acqua. Viceversa, la condensazione di 1 kg di acqua porta a una cessione di Q = 2.25 · 106 J per ogni kilogrammo.
L'elevato calore latente di evaporazione rende l'acqua molto efficace nello spegnimento del fuoco: infatti l'evaporazione dell'acqua in prossimità di un incendio permette di assorbire notevoli quantità di calore alla sostanza che brucia. Inoltre, il vapor acqueo che si crea, avvolgendo il corpo in fiamme, ne ostacola l'afflusso dell'ossigeno necessario per la combustione.

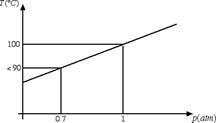Anche nel processo di evaporazione bisogna specificare la pressione alla quale avviene il processo. Ad esempio, la temperatura di evaporazione dell'acqua aumenta all'aumentare della pressione, come emerge dal seguente grafico:
A 0.7 atmosfere (pressione che si ha per esempio a 3000 m di altezza) la temperatura di evaporazione dell'acqua è inferiore a 90°C. Questo è il motivo per cui la pasta in montagna si scuoce. Il fatto che la temperatura di evaporazione diminuisca al diminuire della pressione comporta anche la necessità per gli astronauti nello spazio di indossare delle tute pressurizzate, in grado di evitare l'evaporazione del sangue che altrimenti potrebbe avvenire anche alla temperatura della navicella.
Su questi principi fisici si basa anche la macchinetta per il caffè espresso. La parola stessa espresso deriva da extra pressione. Nella macchinetta del caffè il vapore presente al di sopra dell'acqua genera una pressione sull'acqua che risale per il condotto centrale. La polvere di caffè è stata compressa ed oppone resistenza. In queste condizioni la pressione di vapore cresce, l'acqua bolle a 120°C e la sua capacità di estrarre aroma dal caffè è notevolmente accresciuta. Su meccanismi analoghi si basa il funzionamento della pentola a pressione.

Propagazione del calore

In generale abbiamo visto che, quando forniamo calore ad un corpo, la sua temperatura aumenta oppure, se siamo in prossimità di un cambiamento di stato, la temperatura non aumenta ma il calore viene utilizzato per indurre il cambiamento di fase della sostanza in esame. Ma quando forniamo calore a un corpo, come avviene la propagazione del calore al suo interno?
Esistono tre modi diversi con cui si propaga il calore:

conduzione: avviene nei solidi. L'energia termica viene trasferita attraverso la vibrazione degli atomi che costituiscono il solido ma non c'è trasferimento di materia.
convezione: avviene nei fluidi. L'acqua quando si scalda subisce un processo di dilatazione termica: all'aumentare del volume diminuisce la densità, quindi l'acqua calda tende a salire. Le molecole d'acqua si spostano e si mescolano tra loro (moti convettivi),
irraggiamento: avviene anche in assenza di materia, grazie alla propagazione della radiazione elettromagnetica (ad esempio quella proveniente dal Sole).

Il calore si propaga dal corpo a temperatura più alta a quello a temperatura più bassa in maniera rapida se il materiale ha una elevata conducibilità termica k (ad esempio nei metalli), in maniera lenta se il materiale ha una bassa conducibilità termica (ad esempio negli isolanti).

ELEMENTI DI ELETTROSTATICA

La carica elettrica
La carica elettrica è una proprietà delle particelle che costituiscono gli atomi.
Con questo termine, si identificano i mattoni che costituiscono le molecole. Queste ultime rappresentano l’elemento indivisibile che conserva ancora tutte le proprietà della sostanza in esame. Molte sostanze hanno molecole costituite da singoli atomi. Come abbiamo già discusso, nel caso di alcune sostanze che alla temperatura ambiente sono solide, gli atomi sono organizzati in una struttura ordinata che costituisce il reticolo cristallino.
Dalla discussione sulla struttura atomica risulta che la carica elettrica è trasportata dalle particelle che costituiscono gli atomi in particolare dai protoni e dagli elettroni. Abbiamo anche visto che sia i protoni che gli elettroni trasportano la stessa carica ma di segno opposto:

carica elettrica elementare: e = 1.6·10-19C

Non è stata trovata finora alcuna particella avente una carica più piccola della carica dell’elettrone.
Quindi la carica elettrica è quantizzata, cioè ogni altra carica elettrica sarà un multiplo intero della carica dell’elettrone.

In un sistema isolato, la somma delle cariche positive e negative si mantiene costante. Tale enunciato esprime la legge di conservazione della carica elettrica

Fenomeni di elettrizzazione
Se gli atomi di un corpo acquistano o perdono elettroni, il corpo stesso risulta possedere rispettivamente un eccesso di cariche negative o di cariche positive e quindi risulta elettrizzato.
Un corpo si dice elettrizzato se al suo interno viene a mancare l'equilibrio tra elettroni e protoni, cioè tra cariche negative e cariche positive.
Un corpo può essere elettrizzato in vari modi:per strofinio, per contatto e per induzione.

Elettrizzazione per strofinio:

Certi corpi hanno la proprietà di elettrizzarsi se vengono strofinati con un panno di lana.
Questo metodo viene detto elettrizzazione per strofinio.

Strofinando con un panno di lana il vetro o materiale simile al vetro, in essi si manifesta elettricità positiva: durante lo strofinio si ha un trasferimento di elettroni dal vetro alla lana, perciò il vetro risulta elettrizzato positivamente mentre la lana negativamente.
Strofinando con un panno di lana l' ebanite o sostanze simili, in esse si manifesta elettricità negativa: in questo caso avviene il trasferimento di elettroni dalla lana all' ebanite, perciò quest’ultima risulta elettrizzata negativamente, mentre la lana positivamente

Elettrizzazione per contatto:

L' elettrizzazione per contatto consiste nell' elettrizzare un corpo neutro ponendolo a contatto con uno carico.
Se disponiamo di un oggetto elettricamente carico e lo portiamo a contatto con un corpo neutro attraverso la zona di contatto avviene il trasferimento di un certo numero di cariche elettriche dal primo corpo al secondo.
Poichè subito dopo il passaggio i due corpi presentano elettricità dello stesso segno, essi tenderanno a respingersi.

Elettrizzazione per induzione:

L'elettrizzazione per induzione consiste nel produrre una separazione di cariche in un corpo neutro avvicinando ad esso un corpo carico.
Se accostiamo una bacchetta di vetro, oppure una bacchetta di ebanite elettrizzate a dei pezzetti di carta, questi in entrambi i casi vengono attratti dalla bacchetta.
Questo fenomeno avviene perchè un corpo carico, cioè elettrizzato, è in grado di elettrizzare un corpo neutro, cioè di provocare in quest’ultimo una separazione di cariche per semplice avvicinamento, cioè senza che vi sia stato passaggio diretto di cariche nei due corpi.

Conduttori e isolanti
Rispetto alla capacità di trasportare le cariche elettriche, i materiali possono essere classificati in conduttori e isolanti.
Si chiamano conduttori le sostanze in cui le cariche si possono muovere liberamente, mentre si chiamano isolanti tutte le sostanze in cui le cariche non si possono muovere o si muovono con grande difficoltà.

Sono conduttori tutti i metalli, gli organismi viventi e la grafite; sono isolanti la plastica, il vetro e il legno. I conduttori non possono essere elettrizzati per strofinìo.
Ripetendo l' esperimento d' elettrizzazione per strofinìo con una forchetta metallica, invece che con l' ebanite, si osserva che i pezzettini di carta non vengono attratti.
Possiamo strofinare il metallo della forchetta con la lana quanto vogliamo, ma non sarà possibile esercitare nessuna forza verso la carta.
Questo accade perchè i metalli disperdono velocemente le cariche elettriche acquisite con lo strofinìo. Le cariche infatti si disperdono nel terreno, passando attraverso la mano, il braccio e il corpo di chi l'impugna. Si può ovviare a questo isolando il metallo con un manico di plastica, in questo caso sarà possibile elettrizzare per strofinio anche un metallo.

Nei conduttori gli elettroni sono liberi di muoversi. La causa del comportamento dei conduttori risiede nella struttura dei loro atomi. Gli elettroni non sono fortemente legati ai loro nuclei ma possono muoversi da un atomo all' altro. E' proprio il movimento libero degli elettroni a conferire ai conduttori la proprietà di trasportare l' elettricità.

Negli isolanti gli elettroni sono legati al loro nucleo e difficilmente possono spostarsi da un punto all' altro.

La legge di Coulomb
La forza di attrazione o di repulsione tra due corpi puntiformi carichi elettricamente è direttamente proporzionale al prodotto delle cariche possedute dai due corpi e inversamente proporzionale al quadrato della loro distanza.

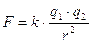
k0 = 9·109 N·m2/C2 Calcolata ne vuoto.

In generale si è portati ad utilizzare un’altra costante, detta costante dielettrica del mezzo considerato: e = 1/4·p·k
mentre con e0 = 1/4·p·k0 si indica la costante dielettrica nel vuoto

er = e / e0 si indica la costante dielettrica relativa ed è sempre maggiore di 1.
e0= 8,85·10-12 C2/N·m2

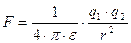
e = e0·er

Corrente elettrica

Definizione di corrente

Nei metalli sono presenti uno o due elettroni per atomo nei livelli più esterni. Questi elettroni sono poco legati ai rispettivi atomi e pertanto sono dotati di una grande mobilità. Quando inseriamo un filo di materiale conduttore in un circuito elettrico, ossia quando colleghiamo il filo ai due capi di un generatore, ad esempio una pila, gli elettroni più esterni, carichi negativamente, si dirigono verso il polo positivo generando in questo modo una grande quantità di cariche in movimento: ha così origine una corrente elettrica.

In particolare, si definisce corrente i il rapporto tra la quantità di carica elettrica Q che passa attraverso una sezione unitaria del circuito, e l'intervallo di tempo Δt in cui questo passaggio avviene: i = Q / Δt. L'unità di misura della corrente nel Sistema Internazionale è l'ampere. Dal momento che la carica Q si misura in coulomb e il tempo in secondi avremo che 1 A = 1 C / 1 s. Per convenzione il verso della corrente coincide con quello in cui si muovono le cariche positive, quindi dal polo positivo al polo negativo del generatore. Quindi il verso della corrente non coincide con il verso del moto degli elettroni.

Per misurare la corrente si usa uno strumento detto amperometro che va inserito in serie con l'utilizzatore X come nella figura di sinistra. Per misurare la differenza di potenziale presente tra due punti, ad esempio ai capi dell'utilizzatore X, dobbiamo usare uno strumento detto voltmetro e inserirlo in parallelo all'utilizzatore X come nella figura di destra:

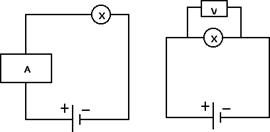
In generale, il ruolo del generatore è quello di mantenere in moto le cariche elettriche all'interno del circuito elettrico fornendo loro l'energia necessaria. Ai capi di ogni utilizzatore ci ritroviamo poi parte di questa differenza di potenziale.

Definizione di resistenza e prima legge di Ohm

Abbiamo visto nella precedente sezione che la differenza di potenziale ΔV fornita dal generatore mette in movimento le cariche elettriche in un circuito dando origine a una corrente elettrica i. A parità di differenza di potenziale applicata, la corrente i che passa in un circuito dipende dalle caratteristiche del materiale conduttore che si è utilizzato. Ogni conduttore manifesta infatti una certa resistenza al passaggio della corrente, dovuta agli urti tra le cariche degli elettroni in movimento all'interno del conduttore e gli atomi delle impurità presenti nel circuito.
In termini matematici si definisce resistenza R di un conduttore il rapporto tra la differenza di potenziale ΔV applicata e l'intensità di corrente i, ossia R = ΔV / i. Dal momento che la corrente i compare al denominatore abbiamo che in un conduttore con grande resistenza R circola una piccola corrente i, viceversa un conduttore con piccola resistenza R è caratterizzato da elevate correnti i. L'unità di misura della resistenza è l'ohm (simbolo Ω, omega maiuscola): 1 Ω = 1 V / 1 A.

In generale, all'aumentare della differenza di potenziale ΔV aumenta anche la corrente i ma ci sono varie possibili relazioni tra i e ΔV a seconda del conduttore che prendiamo in considerazione. C'è però una categoria importante, costituita dai conduttori metallici, per i quali possiamo dire qualcosa di più. Infatti per i conduttori metallici vale la prima legge di Ohm, ossia la differenza di potenziale ΔV ai capi di un conduttore e la corrente i che vi circola sono direttamente proporzionali: ΔV = R · i e la resistenza R è la costante di proporzionalità. La curva caratteristica risulta pertanto una semiretta passante per l'origine:
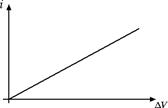Dunque se misuriamo con un voltmetro la differenza di potenziale ΔV e con un amperometro la corrente i scopriamo che in un metallo il rapporto R = ΔV / i è costante. Nei conduttori metallici la resistenza non dipende dalla differenza di potenziale ΔV che applichiamo al conduttore.

Da cosa dipende allora la resistenza in un conduttore metallico? La risposta è data dalla seconda legge di Ohm. La resistenza R in un conduttore metallico dipende dal materiale di cui è fatto il filo, dalla sua lunghezza l e dalla sua sezione A. Più precisamente, R = ρ l / A, ossia la resistenza è direttamente proporzionale alla lunghezza l del filo e inversamente proporzionale all'area A della sezione. La costante di proporzionalità ρ (simbolo che corrisponde alla lettera greca ro) dipende dal tipo di metallo che prendiamo in considerazione e va sotto il nome di resistività. Nella seguente tabella riportiamo la resistività di alcuni metalli comuni:

Metallo	Rame	Argento	Acciaio	Alluminio
ρ (Ω · m)	1.7 · 10-8	1.6 · 10-8	2 · 10-7	2.8 · 10-8

Resistività piccola vuol dire piccola resistenza, ossia buona capacità di condurre elettricità. Dal momento che ρ = R · A / l, l'unità di misura della resistività nel Sistema Internazionale è l'ohm per metro (&Omega · m).

Effetto Joule

Ricordiamo che la potenza assorbita da un utilizzatore è data dalla formula P = ΔV · i. Se il conduttore soddisfa la prima legge di Ohm ΔV = R · i con R costante. In questo caso possiamo perciò riscrivere la potenza assorbita dal conduttore come P = R · i2. Questa formula gioca un ruolo importante nell'effetto Joule che andremo ora a illustrare.

Nel corso delle nostre lezioni di fisica abbiamo più volte parlato di energia. Finora abbiamo introdotto tre diverse forme di energia: l'energia meccanica o lavoro che può a sua volta essere presente sotto forma di energia cinetica, energia potenziale gravitazionale ed energia potenziale elastica. Abbiamo poi introdotto l'energia termica o calore e infine l'energia elettrica. Abbiamo più volte detto che l'energia non si crea e non si distrugge ma si può trasformare da una forma all'altra. L'effetto Joule descrive la trasformazione di energia elettrica in energia termica, ossia in calore.

Se avviciniamo una mano a una lampadina accesa sentiamo del calore, perché la corrente elettrica passando attraverso il filo di tungsteno incontra una certa resistenza R al suo passaggio. La resistenza gioca nei fenomeni elettrici il ruolo dell'attrito, nel senso che ostacola il passaggio delle cariche elettriche. L'energia elettrica che viene convertita in calore per effetto Joule è data dalla seguente formula: Q = P · Δt = ΔV · i · Δt = R · i2 · Δt. Questa legge prende anche il nome di legge di Joule.
Moltissimi sono gli elettrodomestici che si basano sull'applicazione dell'effetto Joule: dalla lavatrice allo scaldabagno, dalla stufa elettrica alla piastra metallica, dal fornelletto all'asciugacapelli al tostapane. Tutti questi elettrodomestici assorbono energia elettrica per convertirla in calore tramite l'effetto Joule. Ricordiamo ora che il calore che forniamo a una certa sostanza di calore specifico c comporta un aumento di temperatura ΔT regolato dalla legge fondamentale della termologia: Q = c m ΔT. Uguagliando questa espressione al calore prodotto per effetto Joule: c m ΔT = R i2 Δt possiamo ad esempio ricavarci l'aumento di temperatura ΔT dell'acqua dello scaldabagno.

Conduttori in parallelo

Nella precedente sezione abbiamo visto che ogni conduttore è caratterizzato da una sua resistenza R. Le resistenze (o, più precisamente, i resistori) sono il secondo utilizzatore che entra nei circuiti elettrici, a fianco dei condensatori. Il simbolo con cui si indica una resistenza in un circuito è . Come i condensatori, anche le resistenze possono essere collegate tra loro in serie o in parallelo. In questa sezione cominciamo ad analizzare il collegamento di due resistenze in parallelo.
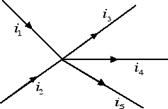Per poter analizzare il collegamento di resistenze in parallelo dobbiamo preliminarmente enunciare il primo principio di Kirchoff. Consideriamo un nodo di un circuito, ossia un punto nel quale convergono più conduttori, come nella figura sottostante.
Il primo principio di Kirchoff afferma che la somma delle correnti che entrano in un nodo è uguale alla somma delle correnti che escono dal nodo: i1 + i2 = i3 + i4 + i5. Il primo principio di Kirchoff è una diretta conseguenza del principio di conservazione della carica elettrica, in base al quale in un certo intervallo di tempo la carica elettrica che entra in un nodo del circuito deve essere uguale alla carica elettrica che esce.
Abbiamo ora tutti gli elementi per studiare il collegamento dei conduttori in parallelo. Supponiamo di avere due resistenze collegate in parallelo come nella figura seguente:

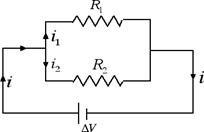
Applicando il primo principio di Kirchoff abbiamo che la corrente i che entra nel nodo è uguale alla somma delle correnti che ne escono: i = i1 + i2. Si definisce resistenza equivalente quella resistenza che, sostituita al posto delle due resistenze in parallelo, produce nel circuito elettrico lo stesso effetto. Per trovare la resistenza equivalente è importante notare come la differenza di potenziale ai capi delle due resistenze in parallelo è la stessa ed è uguale alla differenza di potenziale ΔV fornita dal generatore. Applicando il primo principio di Kirchoff possiamo andare a calcolarci l'inverso della resistenza equivalente: 1 / Re = i / ΔV = (i1 + i2) / ΔV = i1 / ΔV + i2 / ΔV = 1 / R1 + 1 / R2. Dunque se le resistenze sono collegate in parallelo si sommano gli inversi delle resistenze. Nel caso di due sole resistenze abbiamo: Re = (R1 ∙ R2 ) / (R1 + R2 ). La potenza assorbita è invece uguale alla somma delle potenze assorbite: P = i · ΔV = (i1 + i2) ΔV = P1 + P2.

L'importanza del collegamento in parallelo sta nel fatto che il circuito elettrico presente nelle nostre case è un circuito in parallelo: quando accendiamo un elettrodomestico andiamo ad aggiungere una resistenza in parallelo, la resistenza equivalente del circuito diminuisce e in questo modo viene assorbita una quantità maggiore di corrente.

Conduttori in serie

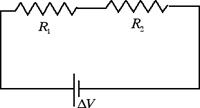In questa sezione vogliamo trovare la resistenza equivalente nel caso di due conduttori collegati in serie, come nella figura seguente
Se colleghiamo due resistenze in serie è l'intensità di corrente ad essere la stessa in tutte le resistenze. La differenza di potenziale (o tensione) fornita dal generatore ΔV si ritrova invece in parte ai capi della prima resistenza ΔV1 e in parte ai capi della seconda resistenza ΔV2. Avremo perciò: ΔV = ΔV1 + ΔV2. La resistenza equivalente Re è data da: Re = ΔV / i = ΔV1 / i + ΔV2 / i = R1 + R2. Dunque nel collegamento in serie le resistenze si sommano.

Anche le potenze assorbite si sommano nel collegamento di resistenze in serie. Infatti la potenza assorbita è data da: P = i · ΔV = i · (ΔV1 + ΔV2) = P1 + P2.
Ora che abbiamo introdotto il collegamento in serie e in parallelo delle resistenze possiamo spendere qualche parola in più sugli amperometri e i voltmetri. Abbiamo già detto che gli amperometri vanno inseriti in serie mentre i voltmetri vanno inseriti in parallelo, come nella figura seguente:

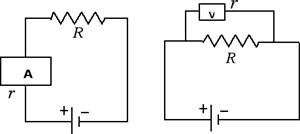
Ora sia l'amperometro che il voltmetro sono dotati di una loro resistenza interna. Cerchiamo di capire come devono essere tali resistenze interne per non interferire con la misura. Cominciamo dal caso dell'amperometro: essendo inserito in serie, la resistenza equivalente è Re = R + r. Affinché la resistenza equivalente non si discosti di molto dalla resistenza R è necessario che la resistenza interna dell'amperometro risulti essere piccola, in modo che Re ≈ R.
Diverso è invece il discorso relativo al voltmetro. Infatti affinché il voltmetro non assorba troppa corrente del circuito è necessario che la resistenza interna del voltmetro sia il più grande possibile. Un altro modo per rendersi conto di ciò è quello di considerare la formula per la resistenza equivalente quando il collegamento è in parallelo: 1 / Re = 1 / R + 1 / r. Affinché la resistenza interna del voltmetro contribuisca il meno possibile alla resistenza equivalente bisogna fare in modo che 1 / r ≈ 0. L'inverso di r è prossimo a zero solo quando la resistenza interna r, che compare al denominatore, è un numero molto grande.

Fonte: http://digilander.libero.it/quantum2008/APPUNTI/dispense%20fisica%20rid.doc
Autore: Prof. Cimmino

Dispensa di fisica