Energia potenziale gravitazionale

 

 

 

Energia potenziale gravitazionale

 

I riassunti, le citazioni e i testi contenuti in questa pagina sono utilizzati per sole finalità illustrative didattiche e scientifiche e vengono forniti gratuitamente agli utenti.

 

L’energia potenziale gravitazionale

Consideriamo un corpo che si trova ad una quota hA rispetto ad un livello terra h=0; su di esso agisce la forza peso .

Il lavoro compiuto dalla forza peso sul corpo quando esso precipita dal livello hA al livello intermedio hB è dato da  dove ∆h=hA-hB è lo spazio percorso in caduta.

Al livello hB il corpo possiede una energia  di tipo cinetico.
Da dove proviene tale energia?
Ovvero ci chiediamo se anche al livello hA esso possedesse una qualche forma di energia che poi è si è trasferita al corpo durante la caduta.
La risposta è affermativa!!

Al livello hA il corpo possedeva una energia UA di tipo potenziale che serviva per mantenere il corpo in quella posizione.
Poniamo  per  definizione.
Quindi il corpo possiede già al livello hA una energia di tipo potenziale pari al lavoro compiuto dalla forza peso P per portare il corpo dal livello hA al livello hB.
Quale sarà l’energia potenziale che compete al corpo nel livello di riferimento considerato hB ?
Seguendo la definizione appena data, essa sarà data dal lavoro compiuto dalla forza peso P per portare il corpo dal livello hB allo stesso livello hB quindi .
Riepilogando abbiamo:

In tutto questo ragionamento abbiamo considerato come livello di riferimento il livello hB , ma nulla ci vieta di considerare come livello di riferimento per esempio la linea di terra h=0 e ripetendo le stesse considerazioni abbiamo che:

Osserviamo che:
La scelta del livello zero di riferimento influisce sul valore dell’energia potenziale in un certo livello, ma non ha nessun effetto sulla differenza di energia potenziale fra due livelli.

 

Quindi in generale possiamo affermare che
La differenza di energia potenziale tra un livello hA e un livello hB di riferimento è data dal lavoro compiuto dalla forza peso P per far cadere l’oggetto da hA a hB

Invece un corpo posto ad un livello hA da un livello di riferimento zero h0 possiede una differenza di energia potenziale:

definita attraverso il lavoro compiuto dalla forza peso P=mg per portare il corpo dal livello h al livello zero.

Ancora più in generale possiamo dire che:
l’energia potenziale posseduta da un corpo di massa m al livello h è:

Osserva che essendo m e g costanti, l’energia potenziale dipende unicamente dalla quota h.
L’unità di misura dell’energia potenziale è il Joule (J).

Fino ad ora abbiamo studiato due tipi di energia meccanica fondamentali: l’energia cinetica K (associata al movimento) e l’energia potenziale U (associata alla posizione).
Nella tabella qui sotto sono riportate i valori dell’energia potenziale e cinetica nel livello di partenza A, in un livello intermedio B e nel livello zero di riferimento.

Sappiamo che:
LA-B = KB –KA                  (per il teorema dell’energia cinetica)
LA-B = UA - UB                (per la definizione di energia potenziale)
E quindi                KB –KA = UA - UB
Cioè                     KB + UB = KA + UA
Quindi possiamo concludere enunciando:
La legge di conservazione dell’energia meccanica E
Durante la caduta l’energia potenziale e l’energia cinetica variano in modo indipendente l’una dall’altra ma in modo che la loro somma sia sempre costante, cioè salvaguardando il bilancio energetico:

questo accade quando il sistema è isolato e le forze sono conservative.
Ricordiamo che una forza si dice conservativa quando il lavoro compiuto dalla forza non dipende dal percorso ma solo dalla posizione iniziale e da quella finale.
La forza peso e la forza elastica sono due esempi di forze conservative.
La forza di attrito non è conservativa.

 

Fonte: http://www.tiby.it/tinti/documenti%20Tinti/8%20energia%20potenziale.doc

 

Autore del testo: non indicato nel documento di origine

 

---

 

Energia potenziale gravitazionale

 

 

 

 

 

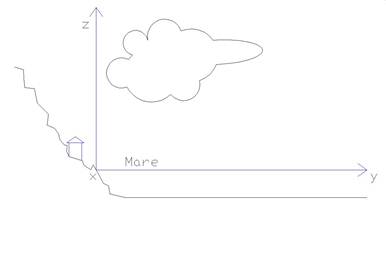
L’energia potenziale gravitazionale è   tipica di un corpo che si trova ad una determinata altezza (z) rispetto al livello del mare che considereremo come livello -0-, o per meglio dire il punto di origine delle forze, in questo caso il campo gravitazionale terrestre (g), come per l’energia cinetica è fondamentale la massa del corpo che prendiamo in considerazione.
La quantità di energia potenziale di un corpo di massa (M), sospeso ad un’altezza (z) e sottoposto ad un’accelerazione di gravità (g) sarà data dalla seguente formula: 

E pot. = M * g * z               e pot. (spec.) = g * z

       

 

 

 

 

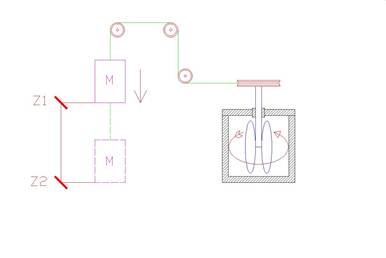
Il seguente esperimento descrive chiaramente il concetto di energia potenziale, dove il peso M si muove dalla posizione z1 alla posizione z2 variando la sua energia potenziale e trasformandola in energia cinetica, la quale tramite un sistema di carrucole sarà trasmessa alla turbina situata nel calorimetro adiabatico, la quale movendosi scalderà l’acqua presente nel calorimetro. L’energia potenziale iniziale si è trasformata in calore o per meglio dire energia termica, immagazzinata nel calorimetro , il quale essendo adiabatico conserverà il calore fino a che non si decida di utilizzare quest’energia termica per produrre lavoro.

Autore: Corrado Capovani

http://www.ramsete.com/DispenseArch01/Capovani139453/Corrado%20Capovani%20matr.%20139453.doc

 

 

Energia potenziale gravitazionale

 

 

Visita la nostra pagina principale

 

Energia potenziale gravitazionale

 

Termini d' uso e privacy