Entropia

 

 

 

Entropia

 

I riassunti, le citazioni e i testi contenuti in questa pagina sono utilizzati per sole finalità illustrative didattiche e scientifiche e vengono forniti gratuitamente agli utenti.

 

IIA LEZIONE DEL 15 NOVEMBRE 2001 (ore 16 - 18):
“L’ENTROPIA”

 

Il disordine

Per determinare se una reazione possa avvenire spontaneamente, sia pure in un tempo illimitato, occorre imparare a misurare l’ordine e il disordine prodotto quando le molecole interagiscono, cioè l’entropia.

Il fatto che una reazione avvenga o no spontaneamente dipende da due grandezze che talvolta cooperano, ma più spesso sono in conflitto tra di loro: il calore o energia e il disordine o entropia. Nel processo di fusione di un ghiacciolo, l’acqua, mediante il congelamento, può perdere calore, passare ad uno stato di minor energia e provocare un incremento dell’ordine nel cristallo di ghiaccio. Al contrario, un ghiacciolo può passare, attraverso il processo di fusione, ad uno stato di maggior disordine, ma solo se gli viene fornito abbastanza calore da rompere i legami idrogeno presenti nei suoi cristalli (fig. 1). I fattori energetici sono dunque a favore del congelamento, mentre quelli entropici sono favorevoli alla fusione. Possiamo perciò affermare che l’energia gioca un ruolo più importante alle basse temperature, mentre l’entropia è il fattore predominante alle temperature più elevate. La temperatura alla quale queste opposte tendenze si bilanciano rappresenta il punto di fusione del ghiaccio.

 

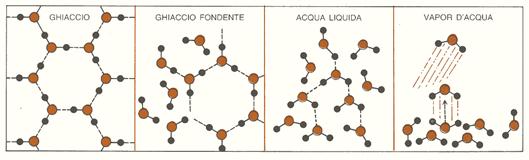
Figura 1: il disordine aumenta passando dal ghiaccio al vapor d’acqua.

Il buon senso dice che i processi spontanei sono quelli che portano alla diminuzione di qualche tipo di energia; ma questo spesso non è vero. La maggior parte delle reazioni chimiche spontanee sono esotermiche, cioè sottraggono energia e la liberano sotto forma di calore. Se solamente questi processi fossero spontanei, allora tutti i gas del nostro universo condenserebbero a liquidi, tutti i liquidi in solidi cristallini e il mondo non sarebbe costituito d’altro che di rocce e ghiaccio. Dobbiamo quindi considerare un secondo fattore nei processi naturali, cioè il disordine; le reazioni spontanee non solo tendono ad andare nella direzione in cui si ha una minor energia, ma anche in quella caratterizzata da un maggior disordine. In alcuni casi le due tendenze si rinforzano a vicenda, in altri il risultato è il compromesso delle due opposte inclinazioni.

La grandezza termodinamica entropia presenta quindi alcune interessanti proprietà: in qualsiasi reazione spontanea o processo reale che avvenga in un sistema isolato (cioè in un sistema in cui energia, calore e materia non possono entrare né uscire) si assiste sempre ad un aumento dell’entropia. Ciò significa che, a parte le considerazioni energetiche, le reazioni spontanee sono quelle che vanno nella direzione di maggior entropia.

Come possiamo misurare il disordine? I mezzi per far ciò provengono dalla fisica studiata intorno alla metà dell’Ottocento da William Thomson (più tardi nominato lord Kelvin) e Rudolf Clausius. Essi furono colpiti dal fatto che l’interconversione di calore e lavoro fosse una strada a senso unico: è facile convertire completamente l’energia in calore, mentre la trasformazione inversa non è mai completa. La versione di Thomson della seconda legge della termodinamica stabilisce che è impossibile, per un qualsiasi processo ciclico e ripetibile, assumere calore e convertirlo completamente in lavoro senza perderne una certa aliquota a favore di un sistema a temperature più basse. La seconda legge fa dunque del calore la forma di energia più degradata, facile da ottenere ma non da convertire.
A livello molecolare, l’energia cinetica è un movimento coordinato di tutte le molecole di un solido nella stessa direzione (fig. 2).

 

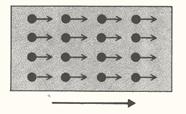
Figura 2.

Il calore di un corpo è il moto scoordinato delle singole molecole attorno alle loro posizioni di equilibrio (fig. 3). L’energia cinetica è un moto organizzato e coerente, mentre il calore è un moto casuale ed incoerente. E’ facile trasformare il primo in secondo, ma è impossibile effettuare il processo in senso opposto.

 

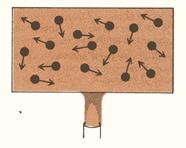
Figura 3.

 

Una delle conseguenze della seconda legge della termodinamica e degli studi di Kelvin e Clausius fu dunque l’invenzione di una nuova ed utilissima grandezza: l’entropia. Secondo la definizione originaria, questa grandezza dipendeva solo da calore e temperatura: con misure calorimetriche, si può determinare l’entropia di qualunque sostanza ad una determinata temperatura. Tali valori vengono denominati “entropie della terza legge” e si possono trovare in tabulati simili allo schema seguente.

 

SOSTANZA	ΔH°298 (Kcal/mole)	ΔG°298 (Kcal/mole)	S°298 (cal/grado·mole)
Na (g)	25,98	18,67	36,72
Na (s)	0,00	0,00	12,20
C (s, diamante)	0,45	0,69	0,58
C (s, grafite)	0,00	0,00	1,36
CH3OH (g)	-48,10	-38,70	56,80
CH3OH (l)	-57,04	-39,75	30,30
CH3OH (aq)	-58,77	-41,88	31,63
NH4Cl (s)	-75,38	-48,73	22,60
H2O (g)	-57,80	-54,64	45,11
H2O (l)	-68,32	-56,69	16,72
HCl (g)	-22,06	-22,77	44,62
HCl (aq)	-40,02	-31,35	13,20

 

Tabella 1: fornisce i valori standard (ΔH°) e le energie libere standard (ΔG°) per la formazione dei composti a partire dagli elementi, nei loro stati standard; vengono inoltre riportate le entropie (S°) termodinamiche di tutti i composti, calcolate secondo la terza legge della termodinamica.
Lo stato fisico del composto è specificato da: (g) = gas, (l) = liquido, (s) = solido, (aq) = soluzione acquosa.

 

Nonostante i dati sperimentali, è per merito di Boltzmann che riusciamo ad interpretare al meglio i valori delle entropie relative usando il concetto di disordine. Egli, come verrà illustrato meglio più avanti, affermò che:

S = K · log W,

dove K è la costante di Boltzmann e W la probabilità di uno stato del sistema, definita come il numero delle possibili configurazioni che danno origine allo stesso stato termodinamico.

I risultati sperimentali ci forniscono alcune significative conclusioni:

1. L’entropia, o disordine, aumenta ogni volta che un liquido o un solido si trasformano in gas (ad esempio nel caso dell’acqua, come si vede in fig. 4, e del sodio metallico, Na).

 

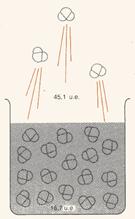
Figura 4: l’acqua evapora a 298 K, con un aumento del disordine di 28,4 unità entropiche per mole.

 

1. L’entropia aumenta quando un solido o un liquido viene disciolto in acqua, come verificabile con il metanaolo liquido, CH3OH (l), e dal cloruro di ammonio cristallino, NH4Cl (s), (fig. 5).

 

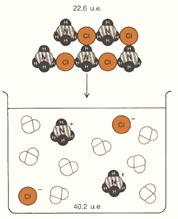
Figura 5: quando dei cristalli di NH4Cl vengono disciolti in acqua, il disordine aumenta di 17,6 unità entropiche per mole.

 

1. L’entropia diminuisce quando un gas viene disciolto in acqua (ad esempio il metanolo, CH3OH (g), come in fig. 6, ed il cloruro d’idrogeno gassosi, HCl (g)).

 

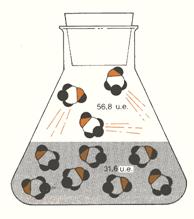
Figura 6: quando viene disciolto metanolo allo stato di vapore in acqua, esso diventa più ordinato di 25,2 unità entropiche per mole

 

1. L’entropia, a parità delle altre condizioni, aumenta all’aumentare della massa.

Questo è un concetto importante, ma difficile spiegare senza l’aiuto della meccanica quantistica. La sua teoria, semplificata, dice che man a mano che aumentano la massa e le dimensioni di un atomo o di una molecola, l’intervallo tra i livelli energetici diminuisce; un corpo grosso e di massa notevole, con una certa energia totale, ha un numero maggiore di stati quantici possibili, perciò W sarà più grande e S = K·log W risulterà maggiore.

1. L’entropia è maggiore nei solidi che possiedono legami covalenti rispetto a quelli con parziale carattere metallico, come si nota per grafite e diamante nella fig. 7: il disordine è inferiore nei solidi ad impalcatura tridimensionale, come il diamante, perché i legami covalenti trattengono gli atomi in una disposizione molto più ordinata rispetto alle forza di attrazione non direzionali presenti nei metalli.

 

1. L’entropia risulta inferiore nelle strutture a strati estesi che nei solidi molecolari.

1. In generale, il disordine aumenta con l’aumentare della duttilità e della debolezza dei legami tra gli atomi; l’aumento dell’entropia e la duttilità sono entrambi indici dello stesso fenomeno, cioè la mancanza di una ben precisa geometria di legami corti che tengono uniti gli atomi.

 

1. L’entropia aumenta con la complessità chimica.

 

I dati derivanti dalla terza legge, sebbene provengano solo da misure termiche, sono in grado di darci alcune informazioni sulla struttura molecolare: queste tendenze delle entropie sono riassunte nella fig. 8, che parte da solidi tridimensionali ed arriva ai gas molecolari. I valori degli elementi puri si trovano invece nella tavola periodica degli elementi.

 

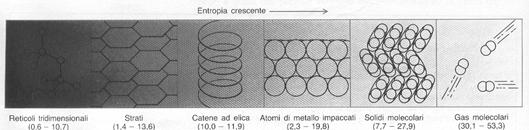
Figura 8: rapporto tra entropia e struttura.

 

Durante una trasformazione, la variazione di entropia del sistema è pari a:

ΔS = S2 – S1 = Q / T,

dove Q è il calore fornito e T la temperatura assoluta del sistema. L’unita di misura del disordine è pertanto: J / K.
Tale formula si ottiene con un ragionamento per assurdo, cioè considerando degli infinitesimi di secondo nel grafico temperatura - tempo (fig. 9).

 

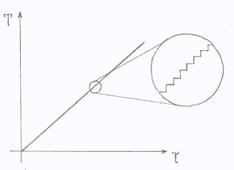
Figura 9.

 

Possiamo inoltre ricavare la variazione di entropia specifica dividendo per la massa:

 

Δs = ΔS / M.

 

Il lavoro perduto in una reazione si ottiene tramite:

 

Lp = T0 · ΔS u,

 

nella quale T0 è la temperatura del termostato più freddo e ΔS u rappresenta la variazione di entropia complessiva dell’universo o di un sistema adiabatico.
Le figure 10 e 11 illustrano ciò che avviene durante trasformazioni isoterme ed adiabatiche: in entrambi i grafici pressione - volume, l’area sottesa dalla curva rappresenta il lavoro; dai diagrammi temperatura – entropia si ricava invece il calore.

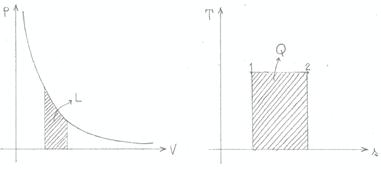
Figura 10: trasformazione isoterma (T = costante).

 

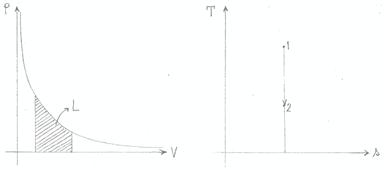
Figura 11: trasformazione adiabatica (Q = costante).

 

Come si può riscontrare direttamente dalla formula:
Δs = q / t,
durante una reazione con calore specifico “q” costante, anche l’entropia specifica “s” rimane invariata.

 

La probabilità

 

L'affermazione secondo la quale i fenomeni spontanei avvengono sempre in una direzione e mai in quella opposta, è dettata da considerazioni di carattere pratico, che derivano dalle osservazioni stesse dei fenomeni, più che dal tentativo di far valere opportune leggi fisiche.
Se scaldiamo una pentola contenente acqua, tutte le molecole iniziano a muoversi sempre più velocemente ma in maniera disordinata. Qual è la probabilità che, per puro caso, le particelle comincino a muoversi tutte nella stessa direzione, trascinando con sé la pentola ed il muro della cucina? Essa è praticamente pari a zero, ma non c’è nessuna legge fisica o chimica che lo vieti: di fatto sono eventi anch'essi possibili. Sono, però, altamente improbabili, ovvero la possibilità che si verifichino è molto piccola.
Si può dire, perciò, che il senso dell'evoluzione dei fenomeni naturali è regolato dalla probabilità: un sistema compie spontaneamente solo e sempre le trasformazioni caratterizzate dalla massima probabilità.
Per chiarire questo concetto consideriamo ad esempio una molecola di gas, racchiusa in un recipiente diviso in due parti A e B da un setto poroso, attraverso il quale la molecola possa passare. Ricordando che la probabilità che si verifichi un evento è data dal rapporto fra il numero di casi favorevoli e il numero di casi possibili, ovvero:
p = numero casi favorevoli / numero casi possibili,
calcoliamo quale sia la probabilità di trovare la molecola di gas nella parte A del recipiente. Come si vede dalla figura 12 c'è un solo caso favorevole su due possibili, dunque si ha:
p = 1/2

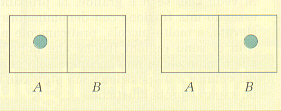
Figura 12.

 

Se le molecole di gas fossero 2, quale probabilità avremmo di trovarle entrambe in A? I casi possibili sono 4, ma solo uno è favorevole (fig. 13), dunque:
p = 1/4 = 1/22

 

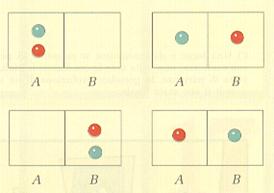
Figura 13.

 

E se le molecole fossero 3? Avremmo 1 caso favorevole su 8 casi possibili (fig. 14), dunque:
p = 1/8 = 1/23

 

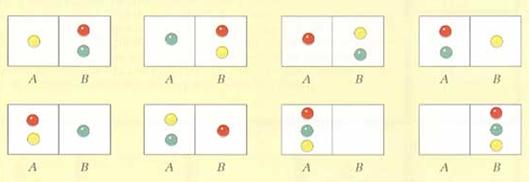
Figura 14.

 

Generalizzando il risultato ottenuto a n molecole di gas, la probabilità di trovarle tutte nella parte A è:
p = 1/2n
Si vede che se n è grande, la probabilità p, essendo una frazione con denominatore molto elevato, è molto piccola, praticamente nulla. Non ci sono ragioni fisiche che impediscano alle n molecole di non occupare solo una parte del volume a disposizione, ma piuttosto esistono ragioni probabilistiche.
Dunque, si può affermare che un sistema evolve spontaneamente verso le configurazioni più probabili, e poiché, come abbiamo visto, l'evoluzione spontanea avviene verso stati in cui l'entropia e il disordine aumentano, ne consegue un nuovo significato dell'entropia, legato alla probabilità: le trasformazioni reali sono caratterizzate da aumento del disordine, aumento dell'entropia, aumento della probabilità.

Come anticipato, l’uomo che ha dato un significato molecolare dell’entropia fu Ludwig Boltzmann, un matematico e fisico che operò nella seconda metà del XIX secolo. Egli suggerì per primo che l’entropia fosse una misura del disordine, e diede un significato concreto a quest’ipotesi proponendo che tale grandezza fosse in relazione con il numero dei diversi modi microscopici attraverso cui si può ottenere una situazione ben determinabile ed osservabile sul piano microscopico. Nella legge:

S = K · log W,

il numero di questi modi di ottenere una situazione è rappresentato da W. La costante di proporzionalità K è la costante dei gas per molecola, cioè:

K = R / N,

in cui R è la costante dei gas e N il numero di Avogadro. K venne scelta da Boltzmann in modo tale che la sua entropia statistica potesse essere espressa dalle stesse unità, e misurata sulla stessa scala dell’entropia termodinamica.
La quantità importante nell’equazione, dal punto di vista fisico, è il numero di modi possibili per ottenere uno stato, W. C’è un solo modo per mettere insieme un cristallo perfetto: uno di essi, allo zero assoluto, ha W = 1 e S = K · log1 = 0. Al contrario, il numero di modi per formare una mole di gas è maggiore che nel caso del cristallo; W è maggiore di 1, e perciò l’entropia risulterà positiva. Qualsiasi situazione definita in maniera tale da poter esser descritta in un solo modo o in pochi modi diversi, viene da noi riconosciuta come ordinata; quando uno stato è definibile attraverso tantissimi modi tutti equivalenti, viene detto disordinato.
Come già anticipato, la legge di Boltzmann ci dice che l’oggetto più perfetto ed ordinato che possiamo immaginare in tutto l’universo è un cristallo perfetto allo zero assoluto. Qualsiasi altra condizione è sicuramente più disordinata ed ha entropia positiva.

 

Autore:  Marta Cavalitti, 140051                                                                                                                    
Giovedì 15 novembre, ore 16 – 18

Fonte: http://www.liceogrigoletti.it/docenti/doc14/files/entropia.doc

 

---

 

Entropia

Entropia (termodinamica)

 

In termodinamica l'entropia è una funzione di stato che si introduce insieme al secondo principio della termodinamica e che viene interpretata come una misura del disordine di un sistema fisico o più in generale dell'universo. In base a questa definizione possiamo dire che quando un sistema passa da uno stato ordinato ad uno disordinato la sua entropia aumenta.

Nel Sistema Internazionale si misura in joule su kelvin (J/K).

 

Storia e definizione

 

Il concetto di entropia venne introdotto agli inizi del XIX secolo, nell'ambito della termodinamica, per descrivere una caratteristica (la cui estrema generalità venne osservata per la prima volta da Sadi Carnot nel 1824) di tutti i sistemi allora conosciuti nei quali si osservava che le trasformazioni avvenivano invariabilmente in una direzione sola, ovvero quella verso il massimo disordine.

In particolare la parola entropia venne introdotta per la prima volta da Rudolf Clausius nel suo Abhandlungen über die mechanische Wärmetheorie (Trattato sulla teoria meccanica del calore), pubblicato nel 1864. In tedesco, Entropie, deriva dal greco εν, "dentro", e da τρoπή, "cambiamento", "punto di svolta", "rivolgimento" (sul modello di Energie, "energia"): per Clausius indicava quindi dove va a finire l'energia fornita ad un sistema. Propriamente Clausius intendeva riferirsi al legame tra movimento interno (al corpo o sistema) ed energia interna o calore, legame che esplicitava la grande intuizione del secolo dei Lumi, che in qualche modo il calore dovesse riferirsi al movimento di particelle meccaniche interne al corpo. Egli infatti la definiva come il rapporto tra la somma dei piccoli incrementi (infinitesimi) di calore, divisa per la temperatura assoluta durante l'assorbimento del calore.

Per chiarire maggiormente il concetto di entropia possiamo presentare alcuni esempi:

 

• Si pensi di far cadere una gocciolina d'inchiostro in un bicchiere d'acqua: quello che si osserva immediatamente è che, invece di restare una goccia più o meno separata dal resto dell'ambiente (che sarebbe uno stato completamente ordinato), l'inchiostro inizia a diffondere e, in un certo tempo, si ottiene una miscela uniforme (stato completamente disordinato). É esperienza comune che, mentre questo processo avviene spontaneamente, il processo inverso (separare l'acqua e l'inchiostro) richiederebbe energia esterna.

• Immaginiamo un profumo contenuto in una boccetta colma come un insieme di molecole puntiformi dotate di una certa velocità derivante dalla temperatura del profumo. Fino a quando la boccetta è tappata, ossia isolata dal resto dell'universo, le molecole saranno costrette a rimanere all'interno e non avendo spazio (la boccetta è colma) rimarranno abbastanza ordinate (stato liquido). Nel momento in cui la boccetta viene stappata le molecole della superficie del liquido inizieranno a staccarsi dalle altre ed urtando casualmente tra di loro e contro le pareti della boccetta usciranno da questa disperdendosi all'esterno (evaporazione). Dopo un certo tempo tutte le moleocole saranno uscite disperdendosi. Anche se casualmente qualche molecola rientrerà nella boccetta il sistema complessivo è ormai disordinato e l'energia termica che ha messo in moto il fenomeno dispersa e quindi non più recuperabile.

Il concetto di entropia ha conosciuto grandissima popolarità nell'800 e nel '900, grazie proprio alla grande quantità di fenomeni che aiuta a descrivere, fino ad uscire dall'ambito prettamente fisico ed essere adottato anche dalle scienze sociali, nella teoria dei segnali e nell'informatica teorica. È tuttavia bene notare che esiste tutta una classe di fenomeni, detti fenomeni non lineari (ad esempio i fenomeni caotici) per i quali le leggi della termodinamica (e quindi anche l'entropia) devono essere profondamente riviste e non hanno più validità generale.

 

Definizione termodinamica

 

L'entropia S come funzione di stato venne introdotta nel 1864 da Rudolf Clausius nell'ambito della termodinamica come

dove ΔQrev è la quantità di calore assorbito in maniera reversibile dal sistema a temperatura T.
In forma differenziale, la legge si presenta così:

È importante notare come, mentre δQrev non è un differenziale esatto, dividerlo per la temperatura T lo rende tale: è dunque il fattore d'integrazione. Occorre sottolineare che dS è un differenziale esatto solo se è valido il secondo principio della termodinamica.
In una delle sue diverse formulazioni, il secondo principio della termodinamica afferma che in un sistema isolato l'entropia può solo aumentare, o al limite rimanere costante per trasformazioni termodinamiche reversibili.

 

Definizione matematica

 

Accanto a questa trattazione dell'entropia, ne esiste un'altra (matematica) che tratta l'entropia come una funzione di stato della sola temperatura, ossia una funzione che dipende esclusivamente dallo stato iniziale e dallo stato finale del sistema e non dal particolare cammino seguito (definita a meno di una costante arbitraria; come l'energia interna, anch'essa funzione di stato).
In quanto funzione continua e monotona crescente della sola temperatura essa ammette un massimo e un minimo assoluti (teorema di Weierstrass) cui l'universo converge con continuità (per il principio di aumento dell'entropia).

L'aumento di temperatura è un fattore strutturale dell'universo. Impossibile è al momento quantificare tale temperatura massima, non essendo noto un legame analitico fra le variabile entropia e temperatura, che nell'intera teoria termodinamica (nei diagrammi T-s) si rappresentano appunto come variabili indipendenti.
Dunque, dell'universo si conosce lo stato inziale a entropia nulla, non lo stato finale a cui converge (a entropia e temperatura massime); la funzione entropia non dipende e non dà informazioni sul cammino che è stato e che sarà seguito per arrivarci, ovvero non ci dice il futuro termodinamico dell'universo. Tuttavia, è possibile inferire alcune ipotesi riguardo al destino ultimo dell'Universo da considerazioni termodinamiche.

 

Energia ed entropia

 

Assumendo che l'intero universo sia un sistema isolato - ovvero un sistema per il quale è impossibile scambiare materia ed energia con l'esterno - il primo ed il secondo principio della termodinamica possono essere riassunti da un'unica frase:

l'energia totale dell'universo è costante e l'entropia totale è in continuo aumento.
valida per qualsiasi sistema isolato.
In altre parole ciò significa che non solo non si può né creare né distruggere l'energia, ma nemmeno la si può completamente trasformare da una forma in un'altra senza che una parte venga dissipata sotto forma di calore.
Se per esempio si brucia un pezzo di carbone, la sua energia si conserva e si converte in energia contenuta nell'anidride carbonica, nell'anidride solforosa e negli altri residui di combustione oltre che naturalmente in forma di calore. Per quanto non si sia persa energia nel processo, sappiamo che non possiamo invertire il processo di combustione e ricreare dai suoi scarti il pezzo di carbone originale.

La spiegazione si trova nel secondo principio della termodinamica che può così essere parafrasato:
ogni volta che una certa quantità di energia viene convertita da uno stato ad un altro si ha una penalizzazione che consiste nella degradazione di una parte dell'energia stessa in forma di calore, in particolare questa parte non sarà più utilizzabile per produrre lavoro.

Lo stato in cui l'entropia raggiunge il massimo livello e non vi è più energia libera disponibile per compiere ulteriore lavoro è detto stato di equilibrio. Per l'intero universo concepito come sistema isolato ciò significa che la progressiva conversione di lavoro in calore (per il principio di aumento dell'entropia totale), a fronte di una massa dell'universo finita, porterà infine ad uno stato in cui l'intero universo si troverà in condizioni di temperatura uniforme; la cosidetta morte termica dell'Universo.
L'entropia caratterizza il verso di qualunque trasformazione reale come trasformazione irreversibile: infatti anche tornando da uno stato finale a uno identico allo stato iniziale (per temperatura, volume, pressione o altri parametri, come continuamente avviene nei cicli di una centrale) almeno una variabile fisica differirebbe dal punto da cui si è partiti, l'entropia (che inevitabilmente aumenta).

Ogni trasformazione reale è una trasformazione irreversibile perché l'entropia aumenta; l'ipotesi di idealità equivale appunto all'ipotesi di una variazione d'entropia nulla.

 

La definizione quantistica dell'entropia

Mentre nella visione classica l'entropia è sempre espressa in termini di variazione, e mai assoluti, in meccanica quantistica è possibile definire l'entropia in termini assoluti, ad esempio attraverso l'entanglement.
Si considerino due sistemi A e B, ognuno con associato uno spazio di Hilbert HA, HB. Il sistema dello stato composito è allora:

In generale, non è possibile associare uno stato puro al componente A. Tuttavia è comunque possibile associarvi una matrice di densità. Sia definito l'operatore proiezione
.
Lo stato di A è la traccia parziale di ρT sulle basi del sistema B:
.
Ad esempio, per lo stato entangled "classico" di A e B, ognuno composto da due stati puri "0" e "1"
.
la matrice densità è

e la matrice densità dello stato puro di A è
.
ossia semplicememte l'operatore proiezione di |ψ〉A. Da notare che la matrice densità del sistema composto, ρT, ha la stessa forma. Ciò non sorprende, in quanto lo stato entangled classico è uno stato puro.
Data una matrice di densità qualsiasi, ρ, possiamo calcolare la quantità

dove k è la costante di Boltzmann, e la traccia è presa sullo spazio H in cui è definita ρ. Risulta che S è esattamente l'entropia del sistema corrispondente ad H.
L'entropia di ogni stato puro è zero, in quanto non vi è indeterminazione sullo stato del sistema. L'entropia di ciascuno dei due sottosistemi A e B entangled è semplicemente kln2, il massimo ammissibile per un sistema a due stati.
Se il sistema nel suo complesso è puro, l'entropia di ogni sottosistema può essere usata per misurarne il grado di "entanglement" con gli altri sottosistemi.
Si può anche mostrare come gli operatori unitari che agiscono su uno stato, come ad esempio l'operatore di evoluzione temporale ottenuto dall'equazione di Schrödinger lasciano invariata l'entropia. Si associa dunque la reversibilità di un processo alla sua variazione di entropia, confermando dunque la teoria termodinamica e, contemporaneamente, l'entropia di un segnale secondo la teoria dell'informazione.

 

La definizione statistica dell'entropia

 

In meccanica statistica l'entropia è il tramite per ottenere inform

azioni macroscopiche a partire dalle configurazioni microscopiche. Intuitivamente si immagina che ad una certa condizione macroscopica di equilibrio del sistema corrispondano una moltitudine di configurazioni microscopiche.
Tali configurazioni microscopiche occupano un volume nello spazio delle fasi il quale viene indicato con Γ. Allora possiamo definire l'entropia "alla Boltzmann" come

dove k è la costante di Boltzmann.
Si può dimostrare che l'entropia così definita possiede tutte le caratteristiche dell'entropia termodinamica ed in modo particolare si dimostra che è estensiva, ovvero gode della proprietà di additività (e differenza: per cui è calcolabile la variazione d'entropia e la funzione entropia è differenziabile, ovvero ha senso parlare di entropia in termini microscopici).
La formula mostra che è estremamente improbabile, anche se non impossibile, che un sistema ritorni da una configurazione finale ad una identica allo stato iniziale.
La differenza fisica di significato tra entropia e temperatura è che la prima misura lo stato di disordine (fisico) del sistema e la seconda, lo stato di agitazione molecolare.
Volendo informazioni macroscopiche del sistema basta derivare l'entropia rispetto una delle sue variabili naturali E, N e V (energia, numero di particelle e volume) tenendo costanti le altre.
È necessario tenere conto che questa trattazione riposa sull'ipotesi ergotica che assicura di poter sostituire la media temporale sulle configurazioni microscopiche con la media sulle configurazioni stesse (propriamente -Gibbs- sostituire le medie temporali con quelle sull'ensemble).

Fonte: http://www.ingsimone.altervista.org/macchine/Entropia.doc
Autore: non indicato nel documento e nel sito web

 

Entropia (S) e deduzione di Gibbs dell’Energia libera (G)

 

Le variazioni energetiche (E o H) che accompagnano una reazione chimica completano la descrizione che noi possiamo dare di una trasformazione e, nella maggior parte dei casi, forniscono delle indicazioni di massima sul verso naturale della reazione, in quanto la maggior parte delle reazioni esotermiche (ed esoergoniche) risulta spontanea.
D'altra parte esistono numerose eccezioni a questo assunto  e  non tutte le reazioni  che  presentano un H (o un E) negativo risultano poi spontanee.
Diventa perciò necessario individuare un criterio di spontaneità che ci permetta di prevedere il verso delle reazioni in modo esauriente e generale.

Inoltre la maggior parte delle reazioni non avviene in modo completo, ma si assesta in uno stato di equilibrio in cui vi è la presenza di una miscela di reagenti e prodotti di reazione in rapporti determinati e calcolabili sulla base dei valori delle costanti di equilibrio.
Dovremo pertanto stabilire un criterio di spontaneità in grado di descrivere non solo il verso naturale di una trasformazione, ma anche di giustificare perché un sistema tende in certe condizioni a raggiungere spontaneamente un punto di equilibrio piuttosto che un altro.

Il criterio generale che permette di prevedere il verso spontaneo di qualsiasi trasformazione, fisica o chimica che sia, e di descrivere la tendenza dei sistemi verso particolari condizioni di equilibrio discende dal secondo principio della termodinamica.

Vi sono diversi modi equivalenti con cui è possibile definire il secondo principio. Uno di questi ci permette di individuare contemporaneamente anche un criterio generale di spontaneità delle trasformazioni: il grado di disordine dell'universo può solo aumentare ed una trasformazione spontanea è sempre accompagnata da un aumento del disordine complessivo dell'universo.

Possiamo dunque prevedere che un sistema non si trovi in equilibrio fino a quando possa modificare il suo stato verso condizioni di maggior disordine complessivo. Esso evolverà spontaneamente verso stati maggiormente disordinati e le condizioni di equilibrio saranno invece caratterizzate da condizioni di massimo disordine.
E' a questo punto evidente che per effettuare delle previsioni relativamente al verso spontaneo delle trasformazioni e al raggiungimento di condizioni di equilibrio, dobbiamo essere in grado di quantificare e misurare il disordine di un sistema.

La funzione di stato in grado di misurare il disordine di un sistema è l'entropia.

Per l'entropia (S) di un sistema, a differenza di quanto avviene per le altre funzioni di stato, è possibile calcolare dei valori assoluti.

Il terzo principio della termodinamica afferma infatti che l'entropia è nulla per gli elementi chimici nella loro forma cristallina allo zero assoluto (0 K).

Il calcolo dell'entropia può essere effettuato utilizzando la relazione di Clausius

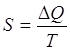
dove
Q = calore scambiato dal sistema
T = temperatura assoluta

 

oppure utilizzando la relazione di Boltzmann

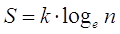
dove
k = costante di Boltzmann (R/N) = 1,38.10-23 J/ K
n = numero di diverse combinazioni di microstati in grado di dare lo stesso macrostato

Nella pratica le misure sperimentali di entropia si eseguono misurando le capacità termiche delle sostanze chimiche a temperature vicine allo zero assoluto (si misura cioè la quantità di calore assorbito per aumentare di 1 grado la temperatura per T 0).
L'entropia si misura in J/ K (Joule su Kelvin).

Le misure sperimentali di entropia per gli elementi allo stato puro a temperature vicine allo zero assoluto forniscono buone conferme del terzo principio della termodinamica (principio di Nernst), confermando che l'entropia di tali solidi cristallini in queste condizioni tende a zero.

I solidi elementari sono infatti formati da atomi tutti identici ed allo zero assoluto essi occupano in modo rigido delle posizioni perfettamente definite all'interno del reticolo cristallino. In queste condizioni il sistema è perfettamente ordinato e vi è un'unica configurazione possibile delle particelle che lo costituiscono. Applicando la relazione di Boltzmann, poiché n = 1,         S = k . ln 1 = 0

 

Le misure sperimentali di entropia per i composti a temperature vicine allo zero assoluto forniscono invece valori di entropia superiori allo zero. Ad esempio l'entropia di 1 mole di ossido di carbonio CO a temperature tendenti a 0 K è pari a 4,6 J/K.
Nel caso di composti chimici infatti le molecole sono composti da atomi differenti. Nel caso dell'ossido di carbonio possiamo ad esempio supporre che le molecole di CO possano disporsi nel reticolo secondo due orientazioni distinte (CO e OC). Se il solido fosse composto da due sole molecole  esse potrebbero dar luogo a 22 = 4 combinazioni diverse. In tal caso   n = 4

CO CO             CO OC           OC CO           OC OC

Se il solido fosse composto da tre molecole  esse potrebbero dar luogo a 23 = 8 combinazioni diverse.
Nel caso in questione, prendendo in considerazione una mole di CO e quindi 6,022.1023 molecole,  il numero di possibili combinazioni è

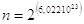
L'entropia teorica, calcolabile attraverso la relazione di Boltzmann è quindi      

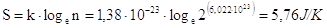
valore in buon accordo con i dati sperimentali.

Man mano che una sostanza viene riscaldata aumenta il suo disordine interno e quindi anche la sua entropia.

Anche per l'entropia è stato fissato uno stato standard che, in analogia a quanto convenuto per l'energia interna e per l'entalpia, è definito come l'entropia di una  mole di sostanza a 25°C e 1 atm (S°). In pratica  l'entropia molare standard di ogni sostanza viene calcolata misurando il calore assorbito da una mole di sostanza alle varie temperature fino ad arrivare a 298 K e sommando poi i diversi apporti calorici da 0 K a 298 K.
Una volta note le entropie standard delle diverse sostanze chimiche è possibile calcolare la variazione di entropia associata ad una reazione chimica come

S° = S°prodotti  -  S°reagenti

Ad esempio nella reazione

N2  +   3H2      2NH3             H° =  - 92,22 kJ

la variazione di entropia della trasformazione è pari a   

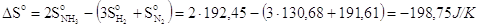
L'entropia del sistema è diminuita. Ciò è dovuto al fatto che i prodotti di reazione sono costituiti da un numero minore di particelle tutte dello stesso tipo, mentre i reagenti sono costituiti da un numero maggiore di particelle e per di più di tipo diverso (azoto e idrogeno). I reagenti possono quindi configurarsi in un numero di modi diversi molto maggiore di quanto non riescano a fare i prodotti di reazione.
In generale possiamo prevedere che l'entropia (e quindi il disordine) di un sistema aumenti durante una reazione chimica quando aumenta il numero delle specie chimiche diverse ed il numero totale delle particelle (o moli) presenti.

Nonostante la reazione di sintesi dell'ammoniaca decorra con una diminuzione dell'entropia del sistema, essa risulta egualmente spontanea a 25°C.
Infatti per poter decidere sulla spontaneità o meno di una reazione non è sufficiente analizzare solo le variazioni di entropia del sistema, ma anche le variazioni di entropia che la trasformazione del sistema genera sull'ambiente.
In altre parole se la variazione di entropia del sistema, sommata alla variazione di entropia dell'ambiente (variazione di entropia dell'universo) indotta da una trasformazione risulta complessivamente positiva, allora la trasformazione risulta spontanea.

Stotale = Ssistema + Sambiente > 0

Nelle reazioni chimiche a pressione costante (la maggior parte) la variazione di entropia dell'ambiente è direttamente collegabile al calore che il sistema scambia con il suo intorno. Così se il sistema subisce una trasformazione esotermica isobara cedendo all'ambiente una quantità di calore Q = H, è possibile dimostrare che la variazione di entropia dell'ambiente (a pressione e temperatura costanti) è pari a

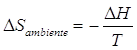
In altre parole è possibile calcolare la variazione di entropia dell'ambiente sulla base delle variazioni di entalpia del sistema.

Il criterio generale di spontaneità di una trasformazione potrà allora essere espresso come

Stotale = Ssistema 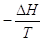 > 0

Comunemente tale relazione viene riscritta nella forma

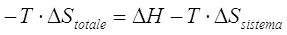< 0

Il prodotto -T.Stotale viene definito come variazione di una nuova funzione di stato, chiamata Energia libera G (da Gibbs, lo scienziato americano che per primo ne propose l'introduzione)

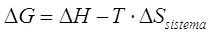< 0
Risulta pertanto spontanea una reazione per la quale la variazione totale di entropia è positiva o, utilizzando la funzione di stato G, per la quale risulti negativa la variazione di energia libera.

 

Fonte: http://didattica-online.polito.it/CHIMICA/dismic/approfondimento/Entropia.doc
Autore: non indicato nel documento

 

Entropia

 

 

Visita la nostra pagina principale

 

Entropia

 

Termini d' uso e privacy