Gas

 

 

 

Gas

 

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

                                

I GAS

 

Il gas è una sostanza che si trova in uno stato caratterizzato dall’assenza di forma e di volume proprio, conseguente alla quasi totale assenza di legami  fra le molecole che la costituiscono e alla distanza relativamente grande tra di esse. Tali condizioni rendono comprimibili i gas entro ampi limiti di temperatura e di pressione.
Comunemente si parla di gas a proposito di sostanze che presentano le caratteristiche  indicate nelle condizioni ambientali di temperatura e di pressione ,mentre si definiscono  vapori le sostanze che ,trovandosi allo stato liquido o solido, si presentano allo stato gassoso  in particolari condizioni  di temperatura e pressione ,ossia alte temperature,basse pressioni,evaporazione,ebollizione,sublimazione.

Sono gas gli elementi nobili:elio,neon,argo,cripto,xeno,e alcuni dei rimanenti idrogeno,ossigeno,azoto,fluoro,cloro,radon, un gran numero di composti,fra cui l’ammoniaca,l’acido cloridrico,l’ossido di carbonio e l’anidride carbonica.

Caratteristica dello stato gassoso è la tendenza di una qualsiasi quantità di gas ad occupare tutto lo spazio a sua disposizione. Conseguenza di questa tendenza è la pressione che un gas esercita sulle pareti di un recipiente che lo contiene o su qualsiasi superficie a contatto con esso.

Ogni sostanza  allo stato gassoso è caratterizzata dalla pressione, dal volume e dalla temperatura alla quale si trova ; queste tre grandezze  non sono però indipendenti fra  di loro ; fissate due di esse , la terza resta completamente determinata .Per conseguenza, assegnato il valore ad una di esse, la variazione di una delle altre due produce la variazione della terza;per esempio.,al variare della pressione a temperatura costante varia  il volume occupato da una determinata quantità di gas.

In adatte condizioni di temperatura  e pressione  i gas possono essere ridotti allo stato liquido  e solido ; reciprocamente i solidi e i liquidi  se non si decompongono prima di aver raggiunto la temperatura necessaria  possono passare allo stato gassoso. Esiste  per ogni sostanza allo stato gassoso una temperatura critica  al di sopra della quale  per quanto sia grande la pressione  applicata ,essa rimane tale e non si liquefa. Si trovano comunemente allo stato gassoso  le sostanze che hanno temperatura critica inferiore a quella ordinaria.

 

Lo studio sistematico  del comportamento dei gas è merito di Robert Boyle il quale attraverso una lunga serie di osservazioni stabilì che ,a temperatura costante;il raddoppio della pressione
esercitata su di una cetra quantità di gas ne riduce il volume alla metà pressione tripla ne riduce il volume ad un terzo  e cosi via , e ne dedusse che il prodotto del volume per la pressione a temperatura costante,è costante :da qui la relazione

pv =K

Questa uguaglianza scoperta quindici anni da Edme Mariotte , va sotto il nome di legge di boyle e Mariotte.
Giova notare che questa legge , e altre proprietà dei gas è valida solo per un gas ideale  e con una buona  approssimazione  per i   gas reali a bassa pressione  e lontani dalla temperatura critica. .
La legge che regola  il cambiamento del volume  al variare della temperatura è stata enunciata nel 1802 da Joseph Lussac,fisico e chimico francese :grazie allo studio di diversi tipi di gas(aria, ossigeno, anidride carbonica ) formulo la legge di Gay Lussac, secondo la quale , a pressione costante:

V = V0(1+aT)

 

Dove V0 è il volume a 0°C, V il volume alla temperatura generica T espressa  in gradi centigradi a rappresenta un coefficiente di espansione :

Dalle misure effettuate ; Gay Lussa  trovò che il coefficiente di espansione  era quasi identico  per tutti i gas studiati e valeva  circa 0,00366°C( almeno a pressione non troppo elevate).Se  rappresentiamo  il volume in funzione  della temperatura otteniamo una  semiretta:il volume  è in correlazione lineare con la temperatura:

 

                                  

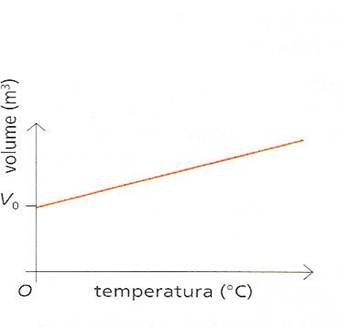
 nello stesso periodo in cui Gay Lussa scopriva la legge che porta il suo nome ; lo scienziato francese Jaches _Alexander Cèsar Charles studiava  il comportamento della pressione dei gas al variare della temperatura :Charles  rilevò  che a volume costante; quando la temperatura di un gas aumenta ,  anche la sua pressione aumenta  viceversa  una dimnuizione di temperatura  fa diminuire la pressione interna del gas .La legge  di Charles , che mette in evidenza  la pressione p con la temperatura T, a volume costante è espressa dalla formula seguente :

                                              p = p0(1+bT)

 

 dove p0 è la pressione alla temperatura di  e b un coefficiente di compressione , Charles scoprì pure  che, a pressioni non troppo alte ,il coefficiente di compressione  era quasi identico per tutti i gas , circa  0,00366 °C^-1, valore identico al coefficiente di espansione  .Nella figura sottostante è presentata  graficamente la legge di Charles : la pressione aumenta  in modo lineare all’aumentare della temperatura .

 

 

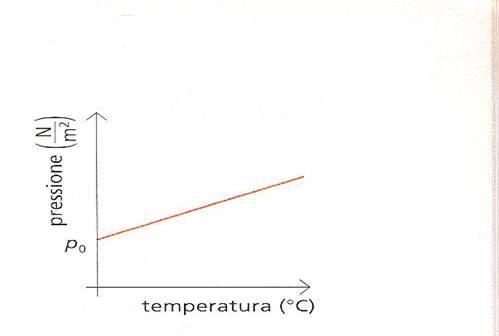
Altra legge che regola i  gas  è la legge di Avogadro ,infatti una mole di gas è quella quantità di gas che contiene  un numero di molecole uguale al numero di Avogadro:

  NA = 6,02 *10^23

All’inizio dell’Ottocento ; il torinese Avogadro , scoprì la legge  che porta il suo  nome   ossia una mole di gas, nelle stesse condizioni di pressione e temperatura, occupa sempre lo stesso  volume , qualunque sia la natura del gas, per esempio , alla pressione di 1atm e alla temperatura di 0°C una mole di qualunque gas occupa un   volume di 22,4 litri.
Come si è gia anticipato precedentemente un gas che segue esattamente le quattro leggi è un gas
perfetto .Nella realtà  non esiste un gas perfetto. Il gas perfetto  è un gas ideale , che aiuta   a capire il comportamento  dei gas reali : Per esempio , l’aria , a temperatura ambiente  e alla pressione atmosferica  si comporta quasi come un gas  perfetto.
Riprendiamo la legge  di Gay-Lussac tenendo presente  la definizione di gas ideale: Considerando un gas ideale  che aumenta la sua temperatura  da 0°C a 100°C.
in un grafico volume _ temperatura  la temperatura sarà rappresentata dalla seguente figura 

 

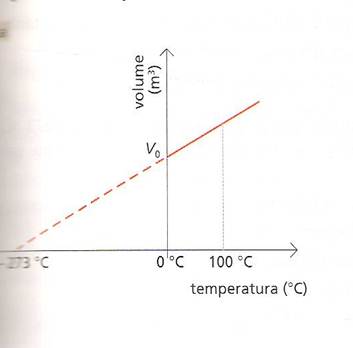
 Utilizzando la legge rappresentiamo l la trasformazione dei gas  anche per temperature inferiori  a 0°C  .        

 Il segmento tacciati  incontra l’asse orizzontale  in un punto che corrisponde  alla temperatura di circa   - 273°C. Per tale temperatura  il volume del gas ideale diventa nullo : Fisicamente  non è
possibile  che il volume di un gas sia nullo ; perché comunque  piccole, le molecole  del gas hanno sempre  certe dimensioni : Perciò  non è neanche possibile  che la temperatura  di un gas risulti inferiore  a – 273°C :A questo valore della temperatura  si dà il nome di zero assoluto:
Si può ripetere lo stesso ragionamento per la legge  di Charles .Utilizzando il grafico pressione – temperatura

 

 

 

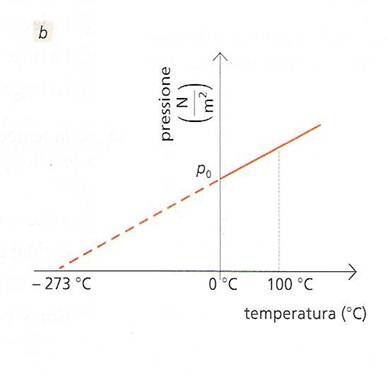
si trova che anche  alla temperatura di  -273 °C la pressione del gas dovrebbe risultare nulla.  
Nell’ 1843 il francese Emilè   Clayperon  dimostrò che le quattro leggi  possono essere riassunte in un’ unica relazione  che lega pressione, volume e temperatura  e quantità di gas:

 

 pV = K NT      

 

dove   N  rappresenta  il numero delle molecole del gas , T  la temperatura in kelvin ; K  è una costante  di proporzionalità identica per tutti i gas  e si chiama costante di Botzlmann.
La relazione viene  chiamata equazione  di stato  dei gas  perfetti  o equazione  caratteristica dei gas perfetti , perché è  sempre vera per i gas  ideali . Per i gas reali, invece , è vera solo quando questi sono a bassa densità , cioè molto rarefatti  e a temperatura lontana da quella di condensazione. Per la legge di Avogadro , una mole di qualunque  gas contiene un numero  di molecole  pari a  6,02 *10ì23 e occupa un volume di 22,4 l  alla temperatura  di 0°C e alla pressione atm. possiamo calcolare quindi  il valore della costante di Botzlmann, in quanto valendo le seguenti uguaglianze :

22,4 litri = 22,4 * 10^-3 m3

0°C =273

1 atm =1,01* 10^5 N/m2

Ricaviamo K dall’equazione di stato:

                                 K= pV /N T

 

Questa costante è identica per i tutti  i gas , perché una mole di qualunque gas ; che  si trova a quella temperatura e a quella  pressione , occupa sempre un volume di 22,4 litri:
Il numero N di molecole di un gas  è sempre molto grande mentre il valore della costante è molto piccolo. Per  questo motivo  l’equazione dei gas perfetti viene espressa in maniera diversa rispetto a quella riportata precedentemente ,si indica con n il numero di moli  del gas . Poichè n moli contengono  un numero N di molecole uguale al prodotto nNA, si può scrivere la formula :               

 

                               pV = nNAKT

 

Indicando con R il prodotto KNA,otteniamo che :

 

                                        pV=nRT

 

La costante R , detta costante universale dei gas, vale 8,31 J/(mole*K)
Supponiamo che un gas passi da uno stato iniziale a uno stato finale ,mentre la pressione p rimane costante. Indichiamo  con Vf e Tf il volume e le temperature finali .Applichiamo  l’equazione  caratteristica dei gas perfetti  allo stato iniziale e allo stato finale:

 

                                                   pVi =nRTi

 

                                           

 

 pVf= nRTf

dividiamo per p:
Vi= nRTi/p

 

                                                   Vf=nRTf/p

 

Poiché nR/p si mantiene costante possiamo scrivere che

                                                V=(cost)T

Questo vuol dire che il volume di un gas ,mantenuto a pressione costante, è direttamente proporzionale alla sua temperatura , espressa in kelvin
Perciò si può rappresentare tutto questo graficamente , il volume in funzione della temperatura , si ottiene una semiretta  che passa per l’origine   

 

 

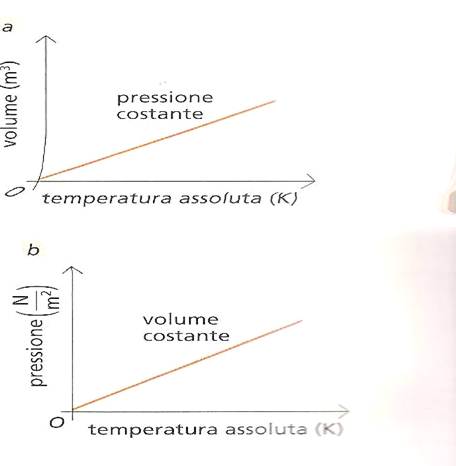
se ripetiamo lo stesso discorso , mantenendo costante il volume invece della pressione, otteniamo che:

 

                                     p=cost T

quindi la pressione di un gas , mantenuto a volume costante, è direttamente proporzionale alla sua temperatura , espressa in kelvin.La rappresentazione grafica della pressione in funzione della temperatura è una semirette che passa per l’origine degli assi .Pertanto è possibile costruire un termometro a gas, sfruttando le variazione di pressione.

 

La teoria cinetica dei gas

La teoria cinetica  dei gas considera  i gas come sistemi costituiti da un grandissimo numero di particelle (molecole o atomi) animate da un continuo movimento , perfettamente elastiche ,e libere di muoversi le une rispetto alle altre senza reciproche interazioni  a distanze relativamente grandi fra loro. Questa schematizzazione vale solo per i gas perfetti , o per i gas realii a temperatura sufficientemente  elevata da rendere trascurabile la coesione delle molecole rispetto alla loro energia cinetica .secondo questo punto di vista , le grandezze macroscopiche o termodinamiche che caratterizzano lo stato e il comportamento di un gas debbono essere interpretate come la risultante statica del comportamento di tutte le particelle che costituiscono il gas.
Nella realtà , nelle condizioni ambiente la maggior parte  dei gas , elementi o composti ,è è formata da molecole , con l’eccezione dei gas nobili;a elevata temperatura  le molecole di numerosi gas si dissociano negli atomi costituenti .
La teoria cinetica stabilisce un nesso fra il comportamento statico di un grandissimo numero di particelle che seguono la legge della meccanica e le grandezze termodinamiche  che caratterizzano lo stato dell’insieme macroscopicamente determinabile. Conseguenza fondamentale di questo nesso è la corrispondenza fra moto delle molecole e temperatura; la

 

temperatura di un gas  è tanto più elevata quanto maggiore è l’energia cinetica media  delle particelle , molecole atomi che lo costituiscono.
Riscaldando un gas  a volume costante gli si somministra  una certa quantità di energia sotto forma di calore che va ad aumentare l’energia cinetica media  delle particelle  che lo costituiscono , e questo fatto  si manifesta in termini  macroscopici , sottraendo invece il calore 
ad un gas nelle stesse condizioni, la diminuzione della temperatura sarà determinata  dalla conseguente diminuzione dell’energia cinetica  delle particelle che formano il gas. Considerando quindi l’energia cinetica si potrà calcolare  la pressione e la temperatura con il modello cinetico . Per esempio considerando un gas monoatomico , varrà la seguente formula :

 

                                              P=2/3 Ecmedia N/V

 

 Dove V è il volume  occupato dal gas  ed N il numero di molecole .
La pressione è proporzionale  alla densità delle molecole :Inoltre la pressione è proporzionale all’energia cinetica media delle molecole, dunque è proporzionale   al quadrato della velocità media delle  molecole
Questa legge stabilisce  un legame fra pressione , volume l’energia cinetica media delle molecole del gas:Pressione e volume sono grandezze macroscopiche , direttamente misurabili, mentre l’energia cinetica media delle molecole è una grandezza microscopica.,
Quindi potremmo calcolarci anche la temperatura con il modello cinetico scrivendo la precedente formula di Bernulli in modo diverso :

                                        pV=2/3NEcmedia

 

ricordando che vale l’equazione di stato dei gas perfetti       

 

                                    

 pV=NKT

dividendo entrambi i membri per 2/3 N otterremo che :

                                        Ec media =3/2 KT

 

Quindi l’energia cinetica  delle molecole è direttamente proporzionale alla temperatura assoluta dei gas .
Le leggi sperimentali di Boyle, di Gay-Lussac e di Charles possono essere interpretate  mediante la teoria cinetica molecolare, tenendo presente  che la pressione di un gas è dovuta ad urti  delle molecole contro le pareti del contenitore.
Supponiamo che il volume a disposizione  di un gas venga ridotto:In tal caso  il numero di urti delle molecole sulle pareti  del recipiente aumenta; perciò il gas  esercita una pressione maggiore  sulle pareti :Il volume  diluisce e la pressione aumenta  in modo che il prodotto delle due grandezze  rimane costante .Pertanto ritroviamo la legge di Boyle.
Se il gas è racchiuso in  un contenitore rigido ; cioè a volume  costante , un aumento della temperatura  produce un aumento dell’energia cinetica media delle molecole .Il numero di urti sulle pareti per unità di tempo aumenta  e perciò aumenta anche la pressione interna  del gas .Ritroviamo la legge di Charles: a volume costante, un aumento della temperatura  produce un aumento di pressione del gas.
Quando la temperatura di un gas aumenta , aumenta l’energia cinetica media delle molecole .Ne deriva che aumenta la frequenza degli urti contro le pareti del recipiente sia la forza che ogni molecola esercita nell’urto. Questi aumenti  tenderebbero a far  aumentare la pressione, ma se essa è mantenuta costante, il gas si espande e quindi aumenta il volume :Ritroviamo la legge di
Gay-Lussac: a pressione costante un aumento di temperatura fa aumentare il volume occupato dal gas.

 

http://www.francescozumbo.it/zumbo/lavori-studenti/2008/cd-5g-2007-2008/lavori/5g-2007-2008-valeria-morabito-gas.doc

autore: Valeria Morabito

 

 

---

 

Gas

 

 

Il gas è uno stato fluido della materia che riempie il recipiente occupato e si lascia facilmente comprimere.
I gas alle stesse condizioni di temperatura e pressione hanno caratteristiche molto simili tra loro.
Le proprietà macroscopiche dei gas sono interpretate attraverso lo studio molecolare e la cosiddetta Teoria cinetica dei gas.
Definiamo la condizione di gas ideale la condizione a cui tutti i gas tendono ad assomigliare diminuendo la temperatura e la pressione. Le proprietà di un gas ideale sono:

• Le particelle del gas ideale non hanno dimensioni, e quindi sono prive di massa: le particelle del gas risultano così pure astrazioni geometriche. Il gas ideale quindi riempie veramente tutto il volume del suo recipiente, mentre il gas reale non lo occupa tutto perché una parte è occupato dal volume delle particelle stesse. Il gas ideale quindi è comprimibile all’infinito (V=0).
• Nel gas ideale le particelle non interagiscono tra di loro.
• Le particelle del gas ideale si muovono di moto rettilineo uniforme urtandosi tra di loro e urtando le pareti del recipiente: ciò si spiega ricordando che non c’è interazione tra le particelle. Gli urti sono elastici, quindi non si perde energia.
• 
  La legge di Graham quindi dice che il rapporto tra la velocità media del primo gas e quella del secondo gas è uguale alla radice quadrata del rapporto tra i pesi molecolari.
  Graham dimostrò questa legge anche sperimentalmente. Abbiamo un tubo di vestro di lunghezza di 1 m, in cui vengono inseriti nello stesso istante dell’Acido Cloridrico HCl e dell’ammoniaca NH3. Avendo un peso molecolare diverso uno sarà più veloce dell’altro (in questo caso acido cloridrico è più pesante e quindi più lento) e si incontreranno a una certa distanza formando sul vetro del tubo un anello bianco di Cloruro di Ammonio (Nh4Cl(s)).
  
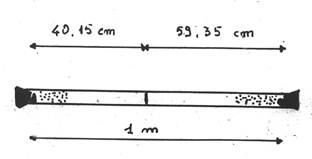
  Si calcola il tempo e quindi la velocità, dimostrando sperimentalmente la validità della Legge di Graham.
  La Legge di Graham può anche essere scritta in un altro modo che è il più usato perché più pratico. Si fa percorrere a due gas differenti uno stesso spazio e si calcola il tempo di percorrenza: esso è proporzionale alla radice quadrata del rapporto tra le masse molecolari dei due gas:
  _tb_ =   ``mb_
                                                                        ta       Ö   ma
  Per poter definire meglio un gas dobbiamo prima definire le sue tre principali variabili : la pressione, il volume, la temperatura.

 

Pressione

Con pressione si intende il numero di urti e la forza F che le particelle hanno contro una determinata superficie s del recipiente
P = _F_ = Newton = 1 Pascal
        S                         m2
Il Pascal è l’unità di misura della pressione e i suoi sottomultipli sono il bar e il mbar.
Bar = 105 Pa   mbar = 102 Pa
Altre unità di misura normalmente usate sono l’atmosfera atm definita come la pressione esercitata da una colonnina di mercurio alta 76cm; altra misura ancora è il torr (in onore del grande fisico Torricelli) definita come la pressione esercitata da una colonnina di Mercurio alta 1 mm. Le unità di conversione sono:
1 atm = 760 torr     1 atm = 101325 Pa

 

Volume

I gas non hanno volume, ma tendono ad occupare interamente il loro recipiente, quindi il volume di un gas è uguale a quello del suo recipiente. Le unità di misura sono il litro L, il millilitro ml oppure il dm3 e il cm3.

 

Temperatura

La temperatura esprime lo stato termico di un corpo.
Nella vita di tutti i giorni la scala usata è quella Celsius, ma nello studio dei gas è usata la temperatura assoluta T (detta temperatura Kelvin) col seguente rapporto di conversione:

 

T = °C + 273

Le Leggi dei Gas

Vediamo ora come varia lo stato di un gas mantenendo prima la temperatura, poi la pressione e infine il volume costanti.

Legge di Boyle

 

 

Boyle si accorse che, mantenendo la temperatura di un gas costante, se si raddoppiava la pressione su questo gas, diminuiva il volume. Egli quindi enunciò una legge che và sotto il nome di Legge di Boyle che dice che la pressione di una gas e il suo volume a temperatura costante sono direttamente proporzionali. Il grafico di questa legge è un ramo d’iperbole.

 

Legge di Charles-Gay Lussac

Charles e Gay-Lussac si accorsero che mantenendo la pressione cotante, intendendo con Vo il volume che il gas ha a 0°C, facendo aumentare la temperatura da 0°C a 1°C il volume aumentava di 1/273 del Vo. Da questa esperienza enunciarono la cosiddetta Legge di Charles- Gay Lussac che dice che il volume di una data quantità di gas in un recipiente mantenuto a pressione costante è direttamente proporzionale alla temperatura assoluta:
V = Vo + 1/273 Vo t
Ponendo a = 1/273 avremo:
                                           V = Vo (1+ a t)      V = Vo aT                             V
Il grafico di questa legge è una retta.
                                                                                                      0°K                                                     T
Da questo grafico per estrapolazione possiamo dedurre qual è la temperatura in cui il volume si annulla, ossia –273,14°C che rappresenta lo zero assoluto della scala Kelvin. Alla temperatura di –273,14°C quindi c’è il gas ideale. A questa temperatura ci si è avvicinati ma non si è mai arrivati, e questo fa capire quanto sia una nozione limite il gas ideale.
Dalla legge di Charles-Gay Lussac si può ricavare una formula più pratica, ossia:
V1 = T1
V2    T2
Dalla legge di Charles e Gay-Lussac si può ricavare un’altra legge: La pressione di una data quantità di gas in un recipiente mantenuto a volume costante è direttamente proporzionale alla temperatura assoluta:
p = po (1+ at)

Legge generale dei gas

La legge generale dei gas vale solamente per i gas ideali e riunisce le leggi di Boyle e Charles-Gay Lussac.
Abbiamo una mole di gas a 0°C con un certo volume iniziale Vo e una certa pressione iniziale po. Facciamo ora subire una trasformazione isobara a questo gas: le sue tre variabili quindi saranno:
0°C    Vo     Po
t°C    V1      Po                       V1 = Voat    [1]
Questa trasformazione è regolata dalla legge di Charles-Gay Lussac.
Facciamo ora invece subire una trasformazione isoterma a questo gas, le tre variabili diventano:
0°C    Vo    Po
t°C     V1    Po
t°C    V2    P                P0V1 = PV2        [2]
Ricavando quindi V1 dalla [2] e sostituendolo nella [1] avremo:
PV = Vo a T po         PV = Vo  po
T       273
Per la Legge di Avogadro noi sapevamo che a 0°C e a 1 atm di pressione, il volume di un gas ideale è 22,414 litri. Quindi sostituendo avremo:
PV = 22,414
273
Quel rapporto è detto costante dei gas ed è uguale a:
R= 0,0821
Siccome noi avevamo n moli, allora la legge generale dei gas è:

PV = nRT

Da questa legge possiamo ricavare le dimensioni di R che sono:
R = 0,0821 l×atm×mol-1×K-1
Se si fa il rapporto membro a membro delle leggi di un gas che cambia tutti e tre i parametri avremo:
                   P1V1 = nRT1        P2V2 = nRT2                      P1V1 = P2V2
                                                                                          T1           T2
Quindi possiamo affermare che la Legge di Boyle è contenuta nella Legge generale dei Gas.
La Legge generale dei gas può essere ancora trasformata e calcolata in funzione della densità di un gas. Infatti se intendiamo il numero di moli come il rapporto tra il peso e il peso molecolare del gas(n = g/M), e la densità il rapporto tra il peso e il volume del gas (d = g/V), avremo
PV = _g_ RT      PM = d RT
M
Ponendo la pressione P = F/S avremo:
PV = F/S V = F×l = Lavoro      L= PV

 

Proponiamoci ora di calcolare alter dimensioni di R:
R = _PV_ = 101325 × 22,414 ×10-3 =  8,314  J × mol-1 × K-1
nT              n    273
Ossia R trasformato in calorie è:
R = 1,987 cal mol-1 K-1

Legge di Dalton sui miscugli gassosi

Dalton studiò un recipiente in cui vi era un miscuglio formato da due gas. Dalton arrivò alla conclusione che La pressione totale a cui è sottoposto un miscuglio è la stessa delle pressioni parziali, intendendo con pressione parziale la pressione che eserciterebbe ogni singolo gas se da solo occupasse tutto il volume del recipiente.
Ptot = P1 + P2
Questa legge è facilmente dimostrabile applicando la legge generale dei gas ai due componenti del miscuglio:
p1 V1 = n1 RT          [1]
p2 V2 = n2 RT          [2]
                                                         (p1 + p2) V = (n1 + n2) RT    [3]                 Ptot = P1 + P2

Frazione Molare

Se facessimo il rapporto membro a membro tra la [1] e la [3] e tra la [1] e la [2], avremo:
_p1_ = _n1_                _p2_ = _n2_
ptot         ntot                  ptot         ntot
Possiamo introdurre così il concetto di frazione molare, cioè in che percentuale è presente nel miscuglio (ossia è la sua concentrazione):
Xi = numero di moli del componente
numero di moli totali
Quindi se consideriamo due gas A e B che compongono un miscuglio, le loro frazioni molari sono:
Xa = ___na__                     Xb = ___nb__            Xa + Xb = na + nb  = 1
na + nb                                na + nb                                             na + nb
Quindi la somma delle frazioni molari dei singoli componenti di un miscuglio è sempre uguale a 1. Quindi un altro modo per scrivere la Legge di Dalton, e per calcolare le pressioni parziali è:
P1 = Ptot Xi               Ptot = å pi

Grado di dissociazione

Dalla legge PM = dRT possiamo ricavare la densità:
d = PM
RT
Si scoprì che in alcuni gas c’era una densità anomala dovuta alla dissociazione. Ad esempio nel Pentacloruro di Fosforo è:
PCl5 « PCl3 + Cl2   (si formano due molecole)
Quindi per correggere la legge generale dobbiamo parlare del grado di dissociazione a:
a = _______n (moli delle molecole dissociatesi)_____
no (moli iniziali prima della dissociazione)
Se si dissociano tutte le molecole allora a = 1, mentre se non se ne dissocia nessuna il grado di dissociazione (sempre espresso in percentuale) è nullo.

 

 

Calcolo del numero totale di particelle

Il numero totale di particelle di un gas è uguale alla somma del numero delle particelle indissociate e del numero di particelle delle dissociazione.
ntot = n (particelle indissociate) + ndiss (particelle della dissociazione)
devo così introdurre n, cioè il numero finale cui dà luogo la dissociazione di una molecola.
ndiss = a × no
ntot = no - ndiss
Se sostituisco il valore trovato prima avremo:
ntot = no (1 - a + an)               ntot = no [1 + a(n-1)]
PV = no[1 + a(n-1)]RT
Questa legge è di validità ancora più generale della legge dei gas.

Gas Reali

Gli esperimenti di Boyle, Gay-Lussac e Charles riguardavano il gas ideale, cioè un gas ala temperatura assoluta, a pressione zero e volume nullo. Il gas ideale è però solamente un’astrazione, in quanto non è possibile raggiungere quelle condizioni di equilibrio.
Infatti se consideriamo il fattore di comprimibilità (Z = PV/RT), esso nei gas ideali è uguale a 1, ma nei gas reali, quelli che si possono trovare in natura, esso è minore di 1.
I gas reali hanno alcune proprietà:                                                            Z

• I gas assomigliano al gas ideale, a bassa pressione
• A media pressione la particella si comprime e il volume è minore

rispetto al volume occupato in uguali condizioni dal gas ideale: per
questo motivo il fattore di comprimibilità è minore di 1. Se dovessimo
quindi rappresentare il fattore di comprimibilità avremo:
Vediamo quindi che se essi si comprimono, arriveranno ad un certo
punto che il loro fattore di comprimibilità comincerà ad aumentare
in quanto le particelle cominceranno a respingersi tra loro, fino ad
arrivare a valori z>1.                                                                                                                           P

• Altra proprietà è che man mano che aumenta la temperatura i gas diventano molto simili al gas ideale.

Equazione di Van der Waals

L’equazione di Van der Waals è l’equazione che descrive i gas reali. Essa è:
(P + _a_) (V – b) = RT
                                                                       V2
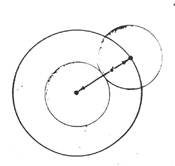
Spieghiamo ora i termini di quest’equazione. Il termine V è il volume a disposizione delle particelle nel gas reale, ed è minore del volume a disposizione delle particelle nel gas ideale. Il termine correttivo b è detto covolume (covolume = spazio occupato dalle particelle)e il suo valore è circa uguale a 4 volte il volume delle particelle. Infatti come si vede nella figura allato i centri di due molecole non possono avvicinarsi ad una distanza inferiore del diametro di una data molecola. Calcolando il volume avremo:
               4/3 p (2 r)3                  4/3 p 8 r3              4[4/3 pr3]
b = 4 Vol N
La Pressione P esercitata dalle particelle nel gas reale minore è minore di quella esercitata dalle particelle nel gas ideale. Il termine a è un termine correttivo ed è dovuto all’effetto delle attrazioni tra le molecole ed è una costante empirica caratteristica del gas considerato.
Il numero di urti con la parete, in un dato tempo, è proporzionale alla densità del gas e ciascun urto è attenuato da una Forza di attrazione verso l’interno del recipiente che è proporzionale alla densità delle molecole che esercitano l’attrazione. In definitiva il fattore di correzione a per la pressione P è proporzionale al quadrato del volume.
P µ urti    P µ Forza di attrazione    P µ d2
d2 µ 1/V2
A bassa pressione il volume del gas è grandissimo, quindi il termine (V-b) è circa uguale a V e inoltre il termine a/V2 è così piccolo che può essere trascurato: quindi a bassissima pressione l’equazione di Van der Waals all’incirca è uguale all’equazione generale dei gas, e quindi il comportamento del gas reale si avvicina a quello del gas ideale.
In definitiva passando dall’equazione di stato PV = RT all’equazione di Van der Waals si è passati da un’equazione unica, valida per ogni gas a comportamento ideale, ad un’equazione valida nella sua forma generale per tutti i gas reali, ma che, per la presenza delle costanti a e b, rappresenta tanti casi diversi quanti sono i gas a cui viene applicata.
Diamo ora di seguito alcune definizioni:
Gas Incoercibili: Sono detti gas incoercibili quei gas che non diventano mai liquidi.
Gas Liquefabili: Sono detti gas liquefabili quei gas che possono diventare liquidi.
Temperatura Critica: Si definisce temperatura critica quella temperatura alla quale il gas si liquefa. Ad esempio l’ossigeno a temperatura di –118°C e con una pressione di 50 atm diventa liquido.
Gas: Viene detta gas una sostanza che ha la temperatura critica al di sotto della temperatura ambiente (25°).
Vapori: Si dicono vapori quelle sostanze che hanno una temperatura critica al di sopra della temperatura ambiente (25°C).

 

Fonte: http://digilander.libero.it/quintaachimica/Gas.doc

Autore del testo: non indicato nel documento di origine

 

 La materia allo stato gassoso (M: 7-1) (P1:5-2):
I gas hanno attratto l'interesse degli scienziati sin dal 1600 ( Robert Boyle). A Boyle si deve la prima delle leggi dei gas:  per una certa quantità di un gas, a temperatura costante, il prodotto della pressione per il volume è costante:

PV = cost.

Il che si può anche esprimere nel modo:

P1V1 = P2V2

cioè che per una certa quantità di gas a temperatura costante la pressione è inversamente proporzionale al volume. La legge di Boyle è una legge limite, cioè che vale come buona approssimazione in alcuni casi e in altri meno buona, mai in modo assoluto per i gas reali. Tutte le leggi dei gas sono perfettamente valide per il gas ideale che è una astrazione,  definita nel modo seguente:

• Le interazioni fra le molecole del gas e fra queste e le pareti del contenitore sono nulle, escluso l’istante in cui collidono.
• Il volume proprio delle molecole del gas è nullo.
• Gli urti tra le molecole e tra queste e  le pareti del contenitore sono perfettamente elastici.
• Tra un urto ed un altro le molecole seguono un moto rettilineo uniforme in qualsiasi direzione dello spazio, cioè in modo del tutto casuale.

Come si è detto, il gas perfetto non esiste in natura. Tuttavia i gas reali tendono ad approssimare il proprio comportamento a quello del gas ideale quanto più bassa è la pressione e quanto più alta è la temperatura.

 

Legge di Charles (1) ( 1787) e di Gay- Lussac (isobara) (2) ( 1802):

• Le variazioni percentuali di volume di gas diversi per una identica variazione di temperatura sono uguali.
• In condizioni isobare, la variazione di volume  di un gas per ogni grado di temperatura                ( aumento se la temperatura aumenta, diminuzione se la temperatura diminuisce) è pari ad 1/273 del volume occupato dal gas alla temperatura di 0°C: Vt  =  V0 ( 1 + αt ), dove Vt è il volume alla generica temperatura t, V0 è il volume del gas a 0°C e α è uguale a 1/273,15.

Legge di Gay-Lussac (isocora):
 In condizioni isocore ( a volume costante), la relazione che intercorre fra pressione e temperatura è analoga a quella fra volume e temperatura: Pt = P0 ( 1 + βt ).
Temperatura assoluta: Se nelle espressioni precedenti poniamo α = β = 1/273,15 e poniamo che (273,15 + t) = T e 273,15°C = T0, otteniamo per V: Vt = V0 ( 1+ t/273,15) =
=V0 ( 273,15 + t )/273,15 = V0 T/T0 cioè Vt/V0 = T/T0, e analogamente per la pressione: Pt/P0 = T/T0. Si è così introdotta una nuova grandezza, la  temperatura assoluta, che ha una scala centigrada, e che si ottiene sommando alla temperatura in gradi Celsius il numero 273,15 e che ha come unità di misura il grado Kelvin. Come si deduce dalle due leggi di Gay-Lussac, valide rigorosamente per il gas ideale, la scala delle temperature assolute ha il suo zero alla più bassa temperatura teoricamente raggiungibile, cioè alla quale il volume e la pressione del gas si azzera. Questa temperatura (-273,15°C) non è praticamente raggiungibile perché il gas ideale non esiste in quanto, per esempio, il volume degli atomi, per quanto piccolissimo, non è tuttavia nullo. Sperimentalmente si sono raggiunte temperature di un millesimo maggiori dello zero assoluto. Una volta definita la temperatura assoluta le due leggi di Gay-Lussac possono essere così ridefinite: 1) A pressione costante (condizioni isobare) la pressione di un gas è direttamente proporzionale alla temperatura assoluta.; 2) A volume costante (condizione isocore) la pressione di un gas è proporzionale alla temperatura assoluta.

Legge di Avogadro (1805) (M:7-1-7):
 Volumi uguali di gas diversi nelle stesse condizioni di temperatura e pressione, contengono lo stesso numero di molecole. Avogadro la ipotizzò nel 1805, per spiegare il comportamento dei gas che, quando si combinano, lo fanno secondo numeri piccoli e interi. La legge si può esprimere anche in questo modo: le masse di volumi uguali di gas diversi, nelle stesse condizioni di temperatura e pressione, sono proporzionali alla massa molecolare di ciascun gas. Poiché la massa (peso) molecolare di una sostanza è data dalla somma dei pesi atomici (relativi) degli elementi che compongono la molecola e questi sono rapportati alla massa di 1/12 dell'isotopo  12C, si può concludere che la quantità di sostanza che contiene la stessa quantità di particelle (molecole, atomi, ioni) contenuta in 12 grammi di carbonio, cioè un numero di Avogadro di particelle pari a N = 6,023 x 1023, sarà uguale al peso molecolare della sostanza espresso in grammi. Questa quantità di sostanza è chiamata mole. La legge di Avogadro si può quindi esprimere con la seguente espressione V = kn, dove k è una costante di proporzionalità ed n è il numero di moli.
Le tre leggi finora discusse si possono così esprimere:

Legge di Boyle: V µ 1/P;

Legge di Charles: V µT;

Legge di Avogadro: V µ n.

Combinando le tre espressioni si ottiene:

V µ nT/P

Chiamando R la costante di proporzionalità si ha:

V = RnT/P ovvero  PV = nRT

Questa espressione è chiamata legge generale dei gas e fornisce la relazione fra le quattro variabili sperimentali di un gas perfetto ( P,V, n, T). La costante R è detta costante universale del gas perfetto e può essere ricavata tenendo conto che, a 0°C e alla pressione di 1 atm., una mole di un gas perfetto ha un volume di 22,414 l, per cui il valore di R, con queste dimensioni ( V in l, P in atm, T in gradi Kelvin), ha il valore di 0,082057.

Pressioni parziali (M: 7-3):
In una miscela di gas, la pressione esercitata da un singolo componente della miscela gassosa
(pressione parziale p) è pari a quella che eserciterebbe se si trovasse da solo ad occupare tutto il volume V a disposizione della miscela. Se si indica con P la pressione totale a cui è sottoposta la miscela gassosa, sarà: P = p1 + p2 +p3 ….+ pn . La legge generale dei gas vale anche perle miscele di gas secondo la. PiV  = niRT. Se si indica con xi la frazione molare (ni/ntot) dell'iesimo componente della miscela sarà pi = xi P.

Interazioni tra molecole nei sistemi gassosi (P2: 6-8):
I gas reali seguono la legge generale dei gas solo a bassa pressione e ad alta temperatura. Queste deviazioni dipendono dalle proprietà intrinseche delle molecole di un gas reale: a) le molecole reali hanno un volume proprio; b) le molecole reali sono soggette ad interazioni reciproche di natura elettrostatica, sia repulsive che attrattive. Quando le distanze sono intermolecolari sono relativamente grandi (superiori al migliaio di pm) queste interazioni sono trascurabili e quindi il gas segue abbastanza fedelmente la legge generale dei gas.  L'andamento dell'energia potenziale dovuta all'azione complessiva delle forze attrattive e repulsive tra due molecole nei sistemi gassosi è espresso dalla funzione potenziale di Lennard-Jones:

E =  Eattr + Erepuls  =  -A/r6 + B/r12

Dove r è la distanza tra due molecole mentre A e B sono parametri che dipendono dal gas considerato. Il primo termine del secondo membro esprime la componente energetica responsabile dell'attrazione tra le molecole. Il valore di questo termine è inversamente proporzionale alla sesta potenza della distanza intermolecolare r, per cui tende a zero già a distanze molto piccole. D’altra parte il valore del secondo termine, che descrive la componente energetica responsabile della repulsione fra le molecole, essendo inversamente proporzionale alla dodicesima potenza della distanza r, si annulla a distanze intermolecolari ancora più piccole, ma al diminuire di queste il suo valore aumenta molto più bruscamente di quanto diminuisca quello derivante dalle azioni attrattive. Il risultato complessivo è che, quando si riduce la distanza tra due molecole prevalgono dapprima le attrazioni intermolecolari, ma a distanze molto brevi predominano le interazioni di natura repulsiva.

Comportamento dei gas ideali (P2 6-8):
I gas reali seguono la legge di Boyle solo a basa presioine e alta temperatura. E’ interessante esaminare l’andamento del fattore di compribilità  (PV/nRT) al variare della pressione:

• Per il gas ideale il f.c. è costante e sempre uguale a 1;
• Pere i gas reali f.c. tende all’unità solo a basse pressioni;
• Di solito il f.c. all’aumentare della pressione dapprima diminuisce raggiungendo un minimo minore di 1 (gas più comprimibile). Poi cresce, diventando maggiore di 1 a pressioni sufficientemente alte.
• Mano a mano che la temperatura cresce, la curva si addolcisce e il minimo si approssima all’asse delle ordinate;
• Esiste una temperatura, detta temperatura di Boyle, alla quale la tangente alla curva PV/nRT contro P, per P = a,0, coincide con la retta che descrive il comportamento ideale. A temperature superiori alla temperatura di Boyle il gas è sempre meno comprimibile del gas ideale).

Gas reali ed equazione di van der Waals (M: 7-4; P2: 6-9):
La teoria cinetica dei gas si basa su due presupposti:

• le molecole del gas abbiano volume proprio nullo;

2) le interazioni fra le molecole del gas siano nulle. Da questi presupposti si sono ricavate le leggi dei gas perfetti che, storicamente, erano state ricavate esclusivamente per via sperimentale.

• Se le molecole di un gas reale hanno un proprio volume intrinseco, esso è precluso al moto delle altre molecole. Se si considerano le molecole del gas come sfere rigide il volume globale di ingombro di una mole (NA) di molecole  si definisce  covolume, b. Il covolume non coincide con il volume fisicamente occupato da una mole di molecole, ma è legato a questo e può essere  calcolato considerando che la minima distanza a cui i centri di due molecole, idealizzate come sfere rigide di raggio r, possono giungere è pari a 2r . Pertanto, per ogni coppia di molecole , c'è una sfera di impenetrabilità il cui volume è  4/3 p (2r)3 = 8 4/3p r3 = 8vm ( vm = volume proprio di una molecola). Per una mole di gas si ricava il covolume b = 4 NA vm. Se indichiamo con Vi il volume che è idealmente a disposizione di n moli di gas e con V il volume del recipiente che contiene il gas sarà: Vi = (V - nb).
• La pressione effettivamente esercitata dalle molecole di un gas sulle pareti del recipiente è inferiore a quella del gas ideale. Infatti ogni molecola che sta per urtare le pareti del recipiente viene attratta, nel gas reale, verso l'interno dalle forze attrattive presenti all'interno del gas. Tanto maggiore è la concentrazione del gas, tanto maggiori saranno queste forze attrattive del gas e tanto meno efficace sarà l'urto della molecola sulle pareti del recipiente. D'altra parte , la pressione dipende, in via diretta, dal numero di molecole che urtano, nell'unità di tempo, le pareti del recipiente; anche questo numero è proporzionale alla concentrazione del gas. L'effetto globale delle interazioni fra le molecole sulla pressione di un gas reale è, pertanto, proporzionale al quadrato della concentrazione del gas n/V. Se si indica con Pi la pressione idealmente prevista e con P la pressione reale del gas, si ha: Pi = P + an2/V2.

Dall'equazione dei gas perfetti si ha allora, per n moli di gas che:

( P + an2/V2 ) ( V - b )  =  nRT

 Questa espressione costituisce l'equazione di Van der Waals che fornisce una approssimazione migliore per i gas reali. Il suo valore non è universale perché le costanti a e b sono diverse per i diversi gas e devono essere ottenute ogni volta sperimentalmente.
A pressioni molto basse il volume del gas è molto grande e la distanza media fra le molecole molto elevata. In questa condizioni sia il covolume b che la pressione interna an2/V2 sono trascurabili e il gas si comporta come un gas ideale. All’aumentare della pressione comincia ad avere peso il contributo della pressione interna, mentre l’effetto del covolume è ancora trascurabile. In altre parole prevalgono le forze attrattive che influenzano la pressione del gas., che diventa più facilmente comprimibile. A distanze brevissime prevalgono le forze repulsive (dalle quali dipendono le dimensioni delle molecole). In queste condizioni diventa importante il covolume, il quale è responsabile del fatto che ad alte pressioni il gas diventa meno comprimibile. Si noti che le interazioni attrattive e il covolume hanno effetti opposti sul fattore di comprimibilità, per cui la localizzazione del minimo di energia dipende da a e da b. Nel caso in cui le attrazioni intermolecolari siano molto deboli può accadere che, ad una data temperatura il minimo tenda a sparire. Ciò accade, per esempio, per l’idrogeno.
Liquefazione dei gas (M: 7-4-2; P2:6-10): L'energia cinetica di un gas, a temperatura sufficientemente alta, è molto più elevata delle energie attrattive tra le molecole, per cui  le molecole sono libere di muoversi liberamente nello spazio a disposizione. Se si diminuisce la temperatura del gas diminuisce pure l'energia cinetica delle molecole fino a quando questa  diventa dello stesso ordine di grandezza delle energie attrattive. Poiché queste crescono con la sesta potenza della distanza, se si comprime il gas le molecole si avvicinano ulteriormente e l'attrazione aumenta ancora, fino a che le energie attrattive prevalgono sui moti termici .A questo punto il gas condensa passando dallo stato aeriforme a quello liquido o solido. A temperature sufficientemente alte, ciò non accade, perché ancora prima che le distanze intermolecolari siano sufficientemente ridotte da far prevalere le energie di attrazione fra le molecole, intervengono le repulsioni fra le nuvole elettroniche. Di conseguenza tra le molecole del gas viene vanificata ogni tendenza ad aggregarsi in una stato condensato. La temperatura critica di un gas (Tcr) è la temperatura al di sopra della quale non è possibile liquefare un gas per sola compressione. Un aeriforme che si trovi al di sotto della temperatura critica viene di solito chiamato vapore, al di sopra viene chiamato gas. Il comportamento di un gas differisce dalla idealità tanto più quanto più si approssima al punto di liquefazione, cioè alla temperatura in cui avviene il passaggio di stato da aeriforme a liquido. Questo fenomeno è dovuto al prevalere delle forze di attrazione intermolecolari sul moto di traslazione delle molecole che è proporzionale alla temperatura assoluta del gas. Il fenomeno della liquefazione è accompagnato dalla emissione di una forte quantità di energia, detta calore latente di liquefazione; conseguentemente l'evaporazione di un liquido (passaggio dallo stato liquido allo stato aeriforme) è accompagnata dall'assorbimento di energia detta calore latente di evaporazione. La compressione di un gas provoca uno sviluppo di calore, perché il lavoro che si compie sul gas viene trasformato in calore. L'espansione di un gas, contro una pressione  esterna, provoca sempre assorbimento di calore, in quanto il gas produce lavoro a spese della propria energia interna. Quando un gas viene espanso nel vuoto, cioè senza produzione di lavoro, se si comportasse  come un gas perfetto, non si avrebbe assorbimento di calore. In pratica la grande maggioranza dei gas si raffredda per espansione. Fanno eccezione solo pochi gas ( idrogeno, elio, neo ) che si riscaldano per espansione nel vuoto. Peraltro anche questi gas, al di sotto di una certa temperatura detta temperatura di inversione, si raffreddano per espansione nel vuoto.

 

Diagramma di Andrews. I dati critici dei gas ( M: 7-4-2-1):
La liquefazione di un gas per semplice compressione può avvenire solo al di sotto di una certa temperatura detta temperatura critica. Diagramma di Andrews: Diagramma isotermo pressione/volume del gas CO2 . Si consideri l'isoterma (a) alla temperatura di 48,1 °C superiore alla temperatura critica del gas  di 31,1 °C. La curva segue abbastanza bene la curva isoterma PV = cost (legge di Boyle), cioè una iperbole equilatera, soprattutto nella sua parte inferiore cioè a bassa pressione. Nella parte superiore, pur seguendo con minor precisione la curva teorica, essa non presenta nessuna discontinuità. La isoterma (e) a 13,1 °C ha un andamento del tutto diverso: Se si segue la curva partendo dalla destra, cioè a bassa pressione, non si riscontra nulla di particolare, sino al punto G dove, a pressione costante, si ha una notevole contrazione del volume, sino al punto B. In questo intervallo tutto il gas passa allo stato liquido, mentre si libera il calore latente di liquefazione. Terminata, dopo il punto B, la liquefazione del gas, per un ulteriore aumento di pressione si ha una minima contrazione del volume in accordo con la poca comprimibilità dei liquidi. La curva, pertanto, segue una linea quasi verticale. Le altre curve  al di sotto della temperatura di 31,1 °C hanno andamento simile. I pianerottoli GB, G'B' ecc., che rappresentano la differenza di volume fra gas e liquido, hanno larghezza sempre minore mano a mano che la temperatura si alza. Esiste una temperatura in cui il pianerottolo della curva P/V si riduce ad un punto, cioè il volume del gas e quello del liquido sono uguali.. A questa temperatura, detta temperatura critica, esiste una pressione, detta pressione critica, alla quale il gas ha lo stesso volume del liquido. Questo volume è detto volume critico. Al di sopra di questa temperatura il gas non si può liquefare per sola compressione. Il calore latente di  evaporazione diminuisce all'aumentare della temperatura sino a ridursi a zero alla temperatura critica.

 

Fonte: http://www.chimica.unipd.it/mario.acampora/pubblica/L59%20.doc

Autore del testo: non indicato nel documento di origine

 

I gas

 

Il termine gas venne coniato agli inizi del ‘600 dal medico e chimico fiammingo Jan Baptiste van Helmont (1577 – 1644), tra i primi a studiare in modo scientifico le caratteristiche di tale tipo di sostanze; egli analizzò in particolare il gas che si sviluppa nella combustione del legno, cui dette il nome di gas silvestre, ciò che noi oggi chiamiamo anidride carbonica. Van Helmont ritenne che questi corpi, privi di una loro forma e di un volume definito, assomigliassero al “caos”, termine con il quale nell’antica Grecia veniva indicata la materia informe e disordinata che era servita, secondo la mitologia, per la creazione dell’universo. Chiamò quindi caos i vapori che otteneva nei suoi esperimenti, ma per adattare la parola alla pronuncia fiamminga adottò la grafia gas, entrata poi nell’uso comune. All’epoca di van Helmont l’unico gas conosciuto era l’aria, che costituiva anche uno dei quattro elementi di cui, seconda la tradizione, sarebbe stata costituita la materia. Spesso, nel corso dei loro esperimenti, gli alchimisti avevano ottenuto alcune “arie” e “vapori”, ma si trattava di sostanze sfuggenti, difficili da studiare ed osservare e facili invece da trascurare.
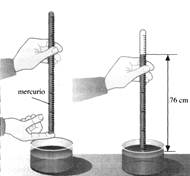
Nel 1643, il fisico toscano Evangelista Torricelli (1608 – 1647), allievo di Galilei, riuscì a dimostrare che l’aria esercita una pressione, corrispondente, in particolare, a quella esercitata da una colonnina di mercurio alta 760 mm, esperimento col quale inventò il barometro .
Ma cosa si intende esattamente per pressione e quali sono le caratteristiche di questa grandezza fisica? Nella vita di ogni giorno noi incontriamo la pressione molte volte ed in svariati differenti contesti: c’è la pressione atmosferica, la pressione delle gomme, la pressione sanguigna ecc. Fisicamente la pressione (P) rappresenta il rapporto tra la forza (F) applicata su una superficie, in direzione perpendicolare ad essa, e l’area (A) della superficie. Per quanto riguarda le unità di misura, ne esistono fondamentalmente cinque, per ognuna delle quali cercheremo di fornire le nozioni essenziali ed i fattori di conversione.

 

 

Grazie a questi esperimenti i gas divennero meno misteriosi: era stato dimostrato infatti che erano composti di materia ed avevano un peso, analogamente ai liquidi ed ai solidi che però erano più semplici da studiare. La pressione esercita dal peso dell’atmosfera fu oggetto di una sorprendente dimostrazione effettuata nel 1654 a Magdeburgo dal fisico tedesco Otto von Guericke, borgomastro della città, il quale aveva inventato una pompa pneumatica, che consentiva di estrarre l’aria da un recipiente, in modo che la pressione atmosferica esterna non venisse più bilanciata dalla pressione interna. Guericke preparò due emisferi di metallo che combaciavano perfettamente lungo un bordo cosparso di grasso; una volta unite le due semisfere ed estratta con la pompa pneumatica l’aria al loro interno, la pressione dell’aria all’esterno le manteneva unite in modo così forte da non poter essere separate neppure dalla forza di alcune coppie di cavalli.

 

Lo stato aeriforme

, il volume (V), la pressione (P) e la temperatura (t). Queste quattro grandezze sono legate tra loro da alcune relazioni fisiche, dette leggi dei gas, che si possono studiare mantenendo costanti due grandezze, facendo variare una terza ed osservando come conseguentemente si comporta la quarta. Ripetendo tale procedimento è possibile giungere a delle relazioni matematiche, che legano le grandezze in esame, ne descrivono il comportamento e riassumono il contenuto delle leggi medesime.

 

 

 

La legge di Boyle

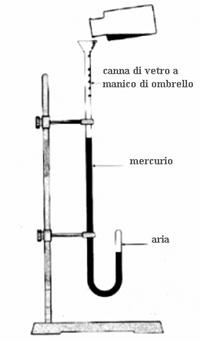
Gli esperimenti di Torricelli e von Guericke suscitarono grande interesse per lo studio dell’aria, attirando in particolare la curiosità di un chimico irlandese di nome Robert Boyle (1627 – 1691). Questi, dopo essere riuscito a costruire una pompa pneumatica ancora più efficiente di quella di Guericke, decise di effettuare l’esperimento opposto, ovvero quello di comprimere l’aria. Per effettuare questa esperienza egli si servi di un lungo tubo di vetro chiuso ad una estremità e piegato a “manico di ombrello”, all’interno del quale versò del mercurio, in modo tale che dell’aria rimanesse imprigionata all’estremità chiusa. Facendo variare il livello di mercurio introdotto nell’estremità aperta Boyle era in grado di variare la pressione esercitata sull’aria all’interno dell’estremità chiusa. Aggiungendo abbastanza mercurio in modo da raddoppiare la pressione esercitata sull’aria, il volume di questa si dimezzava, se la pressione triplicava, il volume si riduceva ad un terzo; se all’inverso riduceva la pressione, il gas si espandeva aumentando il suo volume. 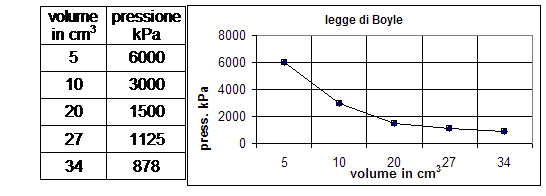Effettuando una serie accurata di misure per numerosi valori di pressione e di volume Boyle si accorse di una cosa fondamentale: in tutte le situazioni il prodotto della pressione per il volume rimaneva costante; volume e pressione erano quindi legati tra loro da una relazione di proporzionalità inversa.

 

 

 

Generalizzando le sue osservazioni nel 1660 egli formulò una legge fisica che può essere espressa matematicamente con l’espressione PV=K. Da un punto di vista storico questo può essere considerato come il primo tentativo di applicare misurazioni esatte alle variazioni di una sostanza di interesse dei chimici, anche se in verità l’esperienza in oggetto descrive una trasformazione fisica e non una trasformazione chimica.  Nel formulare la sua legge il Boyle dimenticò di specificare che essa resta valida solo se la temperatura resta costante.  Il fisico francese Edme Mariotte (1630 – 1684), che nel 1680 scoprì indipendentemente da Boyle la medesima legge, specificò invece chiaramente che la temperatura andava mantenuta costante durante l’effettuazione degli esperimenti. Per tale motivo la legge in questione è conosciuta anche come legge di Boyle – Mariotte ed è definita legge isoterma, in quanto la temperatura resta costante.

 

 

 

Nella legge ora esaminata delle quattro variabili di stato (n, P, V, T), due vengono tenute costanti (n e T), mentre le altre due (P e V) vengono fatte variare l’una in funzione dell’altra. Nell’esperienza di Boyle col tubo piegato a manico di ombrello le variazioni della pressione (variabile indipendente) determinato le variazioni del volume (variabile dipendente). Una relazione del tutto analoga di proporzionalità inversa tra volume e pressione si ottiene però anche effettuando esperimenti inversi a quelli di Boyle, ovvero facendo variare il volume (stavolta variabile indipendente) ed osservando le conseguenti variazioni della pressione (stavolta variabile dipendente). Esperienze di questo tipo possono essere semplicemente svolte con una pompa da bicicletta, nella quale, comprimendo lo stantuffo, il volume diminuisce e la pressione aumenta, facendo uscire l’aria dalla pompa; se viceversa solleviamo lo stantuffo, il volume aumenta e la pressione diminuisce, provocando l’ingresso dell’aria all’interno della pompa.

 

Gli studi di Boyle rilanciarono il dibattito sulla struttura atomica della materia, teoria tutt’altro che accettata ancora alla fine del XVII° secolo . Infatti finché gli studi si concentravano sui liquidi e sui solidi, le testimonianze a favore dell’atomismo restavano all’epoca assai scarse. Solidi e liquidi posso venir compressi solo in misura marginale; se consistono di atomi questi devono essere tanto a contatto tra loro da non poter essere ulteriormente avvicinati. Risulta quindi difficile argomentare che liquidi e solidi devono essere composti da quantità discontinue, ovvero da atomi, in quanto anche se fossero formati da materia continua si otterrebbero gli stessi risultati. Viceversa l’aria, con la sua compressibilità, faceva supporre l’esistenza di particelle separate, atomi appunto, che nella compressione venivano avvicinati, grazie all’eliminazione dei vuoti tra essi interposti. Tuttavia accettando questa concezione dei gas risulta più facile accettare che anche liquidi e solidi siano composti da atomi. Prendiamo ad esempio l’acqua, sostanza ampiamente diffusa in natura e conosciuta da tutti; durante l’ebollizione essa si trasforma in vapore; il vapore acqueo possiede le proprietà fisiche dei gas ed è quindi naturale supporre che sia costituito da atomi. Ma se l’acqua è composta da atomi allo stato di vapore allora lo è composta anche allo stato liquido ed allo stato solido, sotto forma di ghiaccio. Col modello atomico è possibile allora anche spiegare il fenomeno dell’evaporazione dell’acqua, processo durante il quale il liquido lentamente scompare, senza lasciare traccia: ciò può avvenire perché l’acqua si trasforma in vapore atomo per atomo .  Ragionamenti di questo tipo erano molto convincenti ed inoltre se valevano per l’acqua potevano valere anche per altre sostanze; in questo modo l’atomismo cominciò a diffondersi tra gli scienziati dell’epoca tanto che pure Newton divenne atomista. 
Il lavoro di Boyle segna anche il tramonto dei termini alchimia ed alchimista; egli infatti, a partire dal suo libro “The Sceptical Chemist” (Il chimista scettico), pubblicato nel 1661, eliminò la prima sillaba da entrambi i termini. Da allora in poi la scienza venne chiamata chimica e chimici gli scienziati che la praticavano. Boyle si definiva “scettico” perché non era disposto ad accettare le vecchie concezioni, basate solo su speculazioni, in particolare per ciò che riguardava la definizione degli elementi. Questi infatti, fin dall’antica Grecia, erano ritenuti le semplici sostanze primitive di cui era costituito l'universo. Egli ne dette invece una definizione operativa, in base alla quale poteva chiamarsi elemento qualsiasi sostanza che non poteva essere in alcun modo ulteriormente suddivisa; inoltre, se due sostanze erano entrambe elementi, esse si potevano combinare formando una terza sostanza chiamata composto.

 

La legge di Charles

Gli studi sulle proprietà dei gas continuarono dopo il lavoro di Boyle e nel 1787 lo scienziato francese Jacques Charles (1746 – 1823) stabilì che, a pressione costante (legge isobara), il volume di una data quantità di gas aumenta in modo direttamente proporzionale agli aumenti della temperatura. In particolare, per ogni grado centigrado di incremento della temperatura il volume aumenta di 1/273 del suo volume a 0°C, mentre diminuisce con la stessa modalità per ogni decremento di un grado centigrado. Detta legge può essere espressa matematicamente dalla seguente relazione: V=V0 (1+1/273 t), ove V0 è il volume della quantità di gas a 0°C, mentre t è la temperatura in gradi centigradi. Charles, inventore tra l’altro del pallore aerostatico ad idrogeno, non pubblicò mai le proprie osservazioni, che vennero invece rintracciate e pubblicate da Guy Lussac, ragione per la quale la legge isobara è anche conosciuta come legge di Charles e Guy Lussac.
Analizzando la formula che riassume matematicamente la legge di Charles e Guy Lussac si osserva un fatto sorprendente: quando la temperatura raggiunge il valore di – 273 °C il volume del gas va a zero e diventa addirittura negativo per temperature ancora più basse, come si rileva anche dal grafico della pagina successiva. Poiché nessun corpo materiale può avere volume negativo, dobbiamo concludere che in natura la temperatura non può in alcun caso scendere al di sotto di – 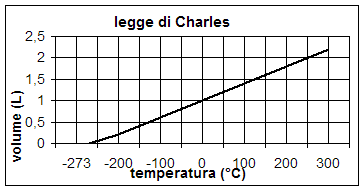273 °C. In base a ciò nel 1894 lo scienziato inglese William Thomson Kelvin (1824–1907) indicò tale temperatura come zero assoluto e definì una nuova scala delle temperature, detta scala delle temperature assolute (T) o semplicemente scala Kelvin, che inizia a partire dallo zero assoluto ed è dotata di un grado unitario della stessa ampiezza della scala Celsius. A partire da ciò la temperatura Celsuis viene indicata con t minuscola, mentre quella Kelvin con T maiuscola; considerando inoltre che misurazioni più accurate hanno fissato lo zero assoluto a – 273.15 °C è possibile passare da una scala all’altra attraverso la seguente relazione matematica: T K = (t + 273.15) °C, da cui deriva altresì che t °C = T K – 273.15.

 

Vediamo adesso, attraverso alcuni semplici passaggi matematici, che forma assume la legge di Charles e Guy Lussac se la temperatura viene espressa in Kelvin.
Poiché sia V0, che 273.15 sono delle costanti, anche il loro rapporto è costante ed è quindi possibile porre V0/273.15 = K. L’espressione della legge di Charles e Guy Lussac diviene quindi V= KT.

 

La legge di Guy Lussac

Continuando il suo lavoro Guy Lussac studiò la relazione che legava la pressione alla temperatura, a volume costante (legge isocora), arrivando alla conclusione che la pressione di una data quantità di gas aumenta in modo direttamente proporzionale agli aumenti della temperatura. Ancora una volta per ogni grado centigrado di incremento della temperatura la pressione aumenta di 1/273 del suo valore a 0°C, mentre diminuisce con la stessa modalità per ogni decremento di un grado centigrado. Detta legge può quindi essere espressa matematicamente dalla seguente relazione: P=P0 (1+1/273 t), ove P0 è la pressione della quantità di gas a 0°C, mentre t è la temperatura in gradi centigradi. Analogamente a quanto abbiamo già visto, se si esprime la temperatura in Kelvin la legge diviene P=KT.

 

 

 

Il principio di Avogadro

Abbiamo già incontrato questo principio lo scorso anno, è tuttavia utile affrontarlo nuovamente in questo contesto, in quanto anch’esso relativo al legame esistente tra le variabili di stato dei gas. Esso infatti stabilisce che, a temperatura e pressione costanti, volumi uguali di gas diverse contengono lo stesso numero di molecole. In altri termini ciò significa che, in condizioni isobare ed isoterme (P e T costanti), il volume V di un qualsiasi gas è direttamente proporzionale alla sua massa, ovvero al numero n di moli. Tale concetto può essere espresso con la seguente relazione matematica: V=Kn.

 

Il modello particellare del gas ideale

Come abbiamo già detto lo scorso anno, le leggi descrivono i fenomeni senza spiegarli. La spiegazione dei fenomeni viene affidata invece ai modelli, rappresentazioni della realtà in grado di spiegare e prevedere i comportamenti della natura. Per spiegare il comportamento dei gas, che viene descritto da tutte le leggi in precedenza affrontate, è stato quindi elaborato un modello di validità generale, detto modello particellare del gas ideale, secondo il quale tutti i gas, indipendentemente dalla loro natura chimica, presentano le  seguenti caratteristiche:

• Le particelle del gas si muovono a grande velocità in tutte le direzioni dello spazio e la velocità aumenta all’aumentare della temperatura.
• Le particelle sono puntiformi ed hanno quindi un volume trascurabile rispetto a quello del recipiente che le contiene.
• Tra le particelle non esistono forze né di tipo attrattivo, né di tipo repulsivo.
• Le particelle si urtano tra loro, ed urtano le pareti del recipiente, in modo perfettamente elastico, ossia senza accelerare né rallentare. La frequenza degli urti sulle pareti del recipiente determina la pressione del gas.

Come premesso, queste caratteristiche fanno riferimento ad un gas ideale. In realtà i gas reali, come l’aria, non rispettano in modo rigoroso questo modello , ma tuttavia tanto più vi si approssimano quanto più sono rarefatti (a bassa pressione) e lontani dalla temperatura di liquefazione, per i gas, o di condensazione, per i vapori; ovvero quanto più sono distanti dalla transizione tra stato aeriforme e stato liquido.
Utilizzando questo modello come chiave interpretativa proviamo quindi ad analizzare nuovamente le leggi dei gas, cominciando da quella di Boyle. A temperatura costante la velocità delle particelle non varia, ma se io riduco il volume riduco lo spazio a loro disposizione: in tali condizioni è logico aspettarsi un aumento della frequenza degli urti con le pareti del recipiente e quindi un aumento della pressione. Viceversa accadrà invece se il volume aumenta.
Per quanto riguarda invece la legge di Charles e Guy Lussac, se la temperatura aumenta, aumenta anche la velocità con cui si muovono le particelle del gas; per continuare ad urtare con la stessa frequenza le pareti del recipiente, mantenendo costante la pressione, esse hanno quindi bisogno di uno spazio maggiore. Se il gas non è contenuto in un recipiente con pareti rigide, esso tenderà ad occupare uno spazio maggiore, cioè a dilatarsi.
Riguardo infine alla legge di Guy Lussac, un aumento della temperatura del gas determina un aumento della velocità delle sue particelle; poiché lo spazio a loro disposizione non può cambiare, gli urti contro le pareti del recipiente sono più violenti e più frequenti e quindi si ha un aumento della pressione.

 

L’equazione di stato dei gas perfetti

Riprendiamo adesso in considerazione le leggi fin qui analizzate, indicando col segno∝la relazione di proporzionalità diretta esistente tra le varie grandezze
Legge di Boyle – Mariotte (n e T costanti) P=K•1/V, quindi P ∝1/V e V∝1/P
Legge di Charles e Guy Lussac (n e P costanti) V=KT, quindi V∝T
Legge di Avogadro (T e P costanti) V=Kn, quindi V∝n
Combinando insieme le tre equazioni otteniamo la seguente relazione generale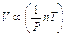e quindi PV=nRT. Questa equazione, detta equazione di stato dei gas perfetti, legando tra loro le quattro variabili di stato che descrivono la condizione di un gas ideale, riassume tutte le leggi fin qui descritte. Come accade per il modello particellare del gas ideale, essa si può applicare anche ai gas reali, a condizione che siano rarefatti e lontani dalle temperature di liquefazione o condensazione.
Esiste in verità anche un modo più rigoroso di ricavare l’equazione di stato dei gas perfetti dalle leggi dei gas, attraverso il procedimento di seguito descritto.
Consideriamo una mole di gas a condizioni standard, ovvero:
P0 = 1 atmosfera   V0 = volume del gas a 0°C (22,4 L)
A temperatura costante (trasformazione isoterma) portiamo la pressione da P0 a P, per la legge di Boyle il volume varierà da V0 a V0’, in modo tale che risulti: V0’ P = V0 P0    (1).
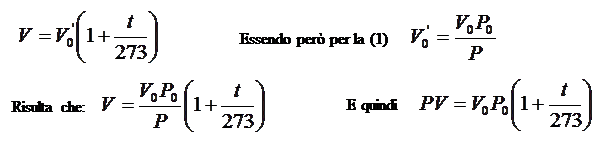A pressione costante (trasformazione isobara) portiamo poi la temperatura da 0°C a t, per la legge di Charles il volume varierà da V0’ a V in modo tale che risulti :

Trasformiamo ora la temperatura Celsius in temperatura assoluta e quindi abbiamo che:

T = t + 273 e quindi t = T- 273

 

 

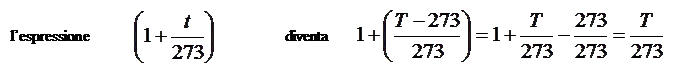
E dunque 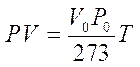       otteniamo  PV=RT

Da qui si ricava l’equazione di stato dei gas perfetti applicabile ad un numero n di molecole:

 

La legge delle pressioni parziali

Il modello particellare del gas ideale è servito finora per spiegare il comportamento dei singoli gas; esso tuttavia può essere impiegato anche per spiegare il comportamento delle miscele di gas . Consideriamo ad esempio una certa quantità di aria, una miscela composta dal 78% di azoto, dal 21% di ossigeno, dallo 0,03% di anidride carbonica, cui si aggiungono altri gas per le percentuali mancanti. Essa occuperà un certo volume all’interno del quale le molecole di ciascun gas sono libere di muoversi indipendentemente dalle altre; ciò farà si che la miscela, nel suo insieme, si comporterà come se ciascun gas occupasse da solo l’intero volume. A questo punto possiamo definire pressione parzialedi un gas in una miscela quella pressione che il gas eserciterebbe se occupasse da solo l’intero volume a disposizione della miscela. E’ facile a questo punto concludere che la pressione esercitata dall’intera miscela sarà data dalla somma delle pressioni che ciascun gas eserciterebbe se occupasse da solo tutto il volume a disposizione della miscela stessa. Tale concetto venne riassunto nel 1807 da Dalton nella sua legge delle pressioni parziali: la pressione che una miscela di gas esercita sulle pareti del suo recipiente è pari alla somma delle pressioni parziali esercitate da ciascun gas della miscela stessa.

 

ESERCIZI SUI GAS

 

• Una massa m di un gas ha una pressione iniziale di 2 atm e occupa un volume di 0,3 L; se viene fatto espandere a T costante fino a farle occupare il volume finale di 1 L quale sarà la sua pressione finale? (R: 0,6 atm)
• Un gas contenuto in una bombola alla temperatura ambiente di 20°C è sottoposto alla pressione di 4,5 atm. Se per esposizione ai raggi del Sole la bombola raggiunge la temperatura di 90°C, quale sarà la pressione del gas? (R: 5,6 atm)
• Una bombola del volume di 50 L contiene 0,03 g di idrogeno (PM 2 g) alla temperatura di 27 °C. Determinare la pressione del gas nella bombola. (R: 7,38 atm)
• 0,28 L di un gas alla temperatura di 265 K esercita sulle pareti del recipiente che lo contiene una pressione di 16 atm. Quanto deve essere compresso il gas affinché la sua pressione sia il triplo? (R: 0.093 L)
• Un gas, posto in un recipiente di 0,8 L, esercita una pressione di 0,56 atm. Se esso viene trasferito, a temperatura costante, in un contenitore del volume di 450 cm3, quale diverrà la sua pressione in Pa? (R: 1.01 105)
• Una certa quantità di gas si trova in un recipiente chiuso alla temperatura di 300 K ed alla pressione di 152 mmHg. Quale sarà la sua pressione in atmosfere dopo che, a volume costante, viene portato alla temperatura di 560 K? (R: 0,373 atm).
• Una certa quantità di gas è contenuta in un recipiente da 2L, alla pressione di 3 atmosfere ed alla temperatura di 127 °C. Che volume occuperebbe il gas se fosse portato a condizioni normali? (R: 4,08L)
• Calcolare la quantità in grammi di Cl2 che occupa un volume di 682 mL alla temperatura di 38,2 °C ed alla pressione di 435 torr. Quale sarebbe la pressione del gas se contemporaneamente la temperatura (misurata in gradi centigradi) triplica ed il volume dimezza? (PM Cl2 70,90 g/mol) (R1 1,083 g di Cl2; R2 1,426 atm)
• Un recipiente da 50 litri contiene un gas, a t = 127 °C e P = 1.520 torr. Calcolare il numero di moli del gas. (R: 0,304 moli)
• Calcolare il volume occupato da 5 g di H2 a: P = 1.000 torr e t = 27 °C. (PM H2 2 g/mol) (R: 46,73 L)
• Calcolare quanto pesano 2litri di O2 a 27 °C e P = 2 atm. (PM O2 32 g/mol) (R:5,22 g)
• Una certa quantità di ossigeno, alla temperatura di 0°C ed alla pressione di 2,0 bar, occupa il volume di 5,0 L. Se scaldiamo il gas fino a 100 °C, mantenendo costante la pressione, quale sarà il suo volume? Se invece manteniamo costante il volume, quale sarà la sua pressione alla nuova temperatura? (R: 6,8 L e 2,7 bar)
• Prendiamo 0,01 m3 di azoto inizialmente a 0°C e raffreddiamoli a pressione costante fino alla temperatura di -50 °C. Quale sarà il volume finale espresso in litri? (R: 8,2L)
• 1 dm3 di aria è conservato all’interno di un recipiente rigido alla pressione di 380 torr ed alla temperatura di 50°C. Cosa succede riscaldando l’aria fino alla temperatura di 100°C? (R: la pressione sale fino a 441 torr.)
• 1 mL di aria, conservata in un recipiente dal coperchio mobile, viene inizialmente posta in acqua bollente. Essa viene poi trasferita in una miscela di acqua e ghiaccio; cosa accade al suo volume? (R: il volume si contrae fino a 0,73mL)
• Una bombola contiene 96L di gas alla pressione di 220 atm. Quanti metri cubi di volume occuperebbe la stessa quantità di gas a pressione atmosferica? (R: 21 m3)
• A 280 K un gas occupa un volume di 75,0 cL; a quale temperatura dovrebbe essere portato, a pressione costante, perché occupasse un volume di 2,50 L (R:933K)

 

 

C:\Documents and Settings\Enrico Campolmi\Documenti\dispense\2°F\gas sf.doc
Fonte: http://www.liceodavincifi.it/_Rainbow/Documents/gas%20sf.doc

 

Autore del testo: non indicato nel documento di origine

 

Gas

 

 

Visita la nostra pagina principale

 

Gas

 

Termini d' uso e privacy