Incertezza ed errori di misura

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Incertezza ed errori di misura

La misura e l'incertezza

Effettuare una misura è senza dubbio un’operazione molto familiare e quotidiana: ogni compravendita ha alla base la misura dell’oggetto di cui si vuole stabilire il prezzo, sia esso la lunghezza di un pezzo di stoffa, oppure il peso di una certa quantità di mele. Le misure sono anche necessarie per la costruzione di una casa o di un mobile. Anche nello sport si misurano i tempi degli atleti nelle varie specialità, mentre per rispondere alla semplice domanda: “che ora è?” diamo un’occhiata a uno dei più diffusi strumenti di misura su cui si basa l’organizzazione della nostra vita sociale: l’orologio. Misurare è quindi un concetto molto intuitivo, sia perché connesso alle necessità pratiche di chiunque, sia perché i vari dispositivi di misura rendono l’operazione tecnicamente semplice: quando vogliamo vedere l’ora basta che diamo un’occhiata alla posizione delle lancette dell’orologio, se vogliamo pesarci basta che saliamo sopra una bilancia e valutiamo dove va a cadere l’indice e così via. La scelta dello strumento adatto e la conseguente semplicità d’uso mascherano in realtà agli occhi dei più il difficile e lungo processo culturale e tecnologico che l’uomo ha seguito nel corso dei secoli prima di giungere a quella che oggi è la semplice misura di un oggetto. Dietro a qualsiasi strumento che noi usiamo tutti i giorni c’è dietro una lunga storia di scienziati, ingegneri o uomini comuni, di teorie scientifiche accettate e teorie scientifiche abbandonate. Se nella vita quotidiana la misura è di estrema importanza, nella fisica assume proprio un ruolo chiave nel progresso delle conoscenze. Quando viene proposta una nuova teoria, essa deve essere verificata per mezzo di esperimenti per i quali la nuova teoria prevede risultati diversi da quelle più vecchie, cioè i risultati sperimentali devono essere in linea con ciò che prevede la nuova teoria e essere in disaccordo con ciò che prevede la vecchia.

Dopo aver descritto le principali caratteristiche degli strumenti di misura, parleremo approfonditamente di che cosa si intende per “errore” o “incertezza” di una misura e di come si valuta.

Il termine “errore” non deve trarre in inganno. Nella scienza la parola “errore” non implica il comune significato di “sbaglio” o “svista”. Come vedremo più avanti, “errore” in una misura scientifica significa l’inevitabile incertezza che è presente in tutte le misure. Il meglio che si possa fare è di assicurarsi che gli errori siano il più ragionevolmente piccoli possibile, e di avere qualche stima realistica di quanto possano essere grandi. Per questo motivo, nonostante la maggior parte dei testi usi la parola “errore”, di qui in poi si preferirà usare la parola “incertezza”.

MISURazioni DIRETTE E INDIRETTE

L’insieme delle operazioni tramite le quali viene eseguito il confronto tra la grandezza da misurare e l’unità di misura viene denominata misurazione.

Il numero che si ottiene dalla misurazione viene detto misura della grandezza.

La misurazione di una grandezza fisica si può effettuare in due modi:

Misurazione diretta: si misura direttamente la grandezza confrontandola con la relativa unità di misura attraverso uno strumento, il quale ci fornisce immediatamente il risultato.

Misurazione indiretta: non sempre le grandezze vengono misurate direttamente. Spesso, per misurare una grandezza, se ne misurano altre direttamente, e da queste poi, con un calcolo, si ricava il valore della grandezza cercata. In questo caso si dice che si è effettuata una misurazione indiretta della grandezza. I motivi per cui una misurazione viene eseguita indirettamente possono essere diversi: perché una misurazione diretta sarebbe più difficile, meno precisa, o semplicemente impossibile. Un esempio molto comune è costituito dalla misurazione del raggio di un oggetto di forma circolare (un tubo, una moneta, ecc.): è molto difficile farne una misurazione diretta; è molto più semplice misurare in modo diretto il diametro e calcolare il raggio usando la formula r = d/2. Un altro esempio è costituito dalle misurazioni di aree o di volumi. Misurarli direttamente è molto difficile; se la superficie di cui dobbiamo misurare l’area ha una forma regolare, è molto meglio fare una misurazione diretta di qualche lunghezza e poi calcolare l’area con un’opportuna formula di geometria. Un terzo esempio si ha nel caso in cui si debba misurare la distanza tra due punti inaccessibili, come capita sempre in astronomia. Facciamo notare che una stessa grandezza può essere misurata sia direttamente che indirettamente; un esempio è la densitàdi un liquido che può essere determinata o attraverso un densimetro (misurazione diretta) oppure misurando massae volume del liquido e utilizzando quindi la relazione d = m/V
In tecnologia si usa il termine “misurazione indiretta” anche per esprimere un altro procedimento di misura che però, lo diciamo per evitare confusione, non ha niente a che vedere con il concetto espresso in precedenza; in tale disciplina si dice che si effettua una misurazione indiretta anche quando si rileva la grandezza da misurare tramite uno strumento intermediario (o ausiliario) e si riporta poi tale misura in un secondo momento sullo strumento misuratore. Per esempio, se vogliamo misurare una certa lunghezza prima si può rilevare tale lunghezza con un compasso allargandolo in maniera tale che le due aste sia il più possibile uguale alla lunghezza da misurare, e in un secondo momento si appoggerà il compasso su, per esempio, una riga per misurare il valore di tale lunghezza.

CARATTERISTICHE DEGLI STRUMENTI DI MISURA

Un apparecchio o strumento di misura è un dispositivo che consente di operare il confronto tra la grandezza fisica e una sua unità di misura e di fornire il risultato di tale confronto. Per esempio, una bilancia elettronica trasforma la misura di massa in un impulso elettrico che può essere trasformato in un numero letto sul display numerico. Uno strumento di misura si dice tarato o a lettura diretta quando i valori riportati sulla scala graduata o sul display numerico corrispondono direttamente al valore della grandezza in esame. Per avere un’idea di uno strumento non tarato, potete pensare a una bilancia a piatti in cui non sia presente alcuna scala graduata: mediante essa è possibile stabilire se un oggetto ha una massa maggiore di un altro, ma non si può misurare la sua massa. La taratura di uno strumento è quindi quell’insieme di operazioni che devono essere compiute per collocare una scala graduata su uno strumento in modo da rendere possibile la valutazione quantitativa di una grandezza fisica tramite la posizione di un indice o tramite la visualizzazione su un display.

Gli strumenti di misura si dividono in due categorie:

Analogici: sono quegli strumenti nei quali il risultato della misura si legge su una scala graduata. Sulla scala graduata può scorrere un indice mobile che può essere di vario genere: vi sono indici costituiti da una lancetta mobile, altri da un sottile fascio luminoso, altri ancora dal bordo estremo di un liquido, ecc.. oppure può scorrere un nonio come per esempio nel calibro. Su un comune righello millimetrato lungo la scala non scorre nulla perché siamo noi a vedere il punto lungo la scala dove va a finire l’oggetto da misurare. I segni posti lungo la scala si chiamano incisioni o tacche, mentre le spaziature tra una incisione e l’altra si chiamano divisioni.

Digitali: (dall’inglese digit = cifra) hanno un display sul quale viene visualizzato il risultato della misura direttamente in cifre. Gli strumenti digitali sono più facili da leggere ma non bisogna pensare che siano in assoluto migliori di quelli analogici.

Le caratteristiche principali di uno strumento di misura sono:

Portata: è il massimo valore della grandezza che può essere misurato dallo strumento. Se lo strumento è dotato di una scala, la portata è indicata dall’ultimo numero presente sulla scala stessa in corrispondenza dell’ultima tacca, ed è perciò spesso, seppur impropriamente, chiamata fondo scala. La portata ha come unità di misura quella della grandezza che lo strumento può misurare. L’utilizzo dello strumento al di sopra della sua portata può rischiare di danneggiarlo seriamente; in ogni caso i valori che si leggono possono non essere più collegati alla misura della grandezza in esame. Quindi è importante, prima di utilizzare un dato strumento, assicurarsi se è in grado di sopportare il valore più elevato che prevediamo possa raggiungere la grandezza fisica da misurare. Osserviamo che alcuni strumenti possono avere più portate intercambiabili (esempio i tester), consentendo la misura ad un campo abbastanza esteso.
Risoluzione: è la più piccola variazione della grandezza che lo strumento può rilevare.
Negli strumenti che hanno una scala graduata, la risoluzione è data dalla differenza tra i valori rappresentati da due tacche consecutive della scala, cioè il valore di una divisione della scala. Osserviamo che in un certo senso portata e risoluzione sono caratteristiche contrastanti; se abbiamo bisogno di una portata molto grande, sarà difficile che riusciamo ad avere una piccola risoluzione. Viceversa, se abbiamo bisogno di una piccola risoluzione, in generale avremo una portata piuttosto bassa.
Se abbiamo a che fare con uno strumento analogico, la formula per calcolare la risoluzione (ma non è l’unica, come si vedrà in seguito) è:

Risoluzione: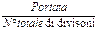
Sensibilità: numericamente la sensibilità è l’inverso della risoluzione. Quindi si calcolerà con la formula:
Sensibilità: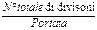
La sensibilità indica di quante divisioni si sposta l’indice quando lo strumento misura l’unità della grandezza in esame. Per esempio, per una bilancia con una risoluzione di 0,5 kg/divisione la sensibilità sarà 1/0,5 = 2 divisioni/kg che sta a significare che quando lo strumento deve misurare 1 kg l’indice si sposta di 2 divisioni. Invece, una bilancia con risoluzione di 100 g, cioè di 0,1 kg, avrà una sensibilità di 1/0,1 = 10 divisioni/kg che sta a significare che quando lo strumento deve misurare 1 kg l’indice si sposta di 10 divisioni. Capite che la seconda bilancia è più sensibile perché a parità di valore misurato il suo indice si sposta di più.
Valore di soglia: corrisponde al valore minimo che lo strumento può misurare. Bisogna fare attenzione a non confondere il valore di soglia con la risoluzione: quest’ultima fa riferimento alla variazione minima che lo strumento può rilevare, mentre il valore di soglia indica il valore minimo misurabile dallo strumento.
Intervallo di funzionamento (o campo di misura): è l’intervallo compreso tra il valore di soglia e la portata. Per esempio, la riga da disegno ha un intervallo di funzionamento da 1 mm a 60 cm.
Prontezza o tempo di risposta: è il tempo che lo strumento impiega a posizionarsi sul valore della misura, una volta messo in contatto con la grandezza in esame. Esso può anche venire definito come il tempo che lo strumento impiega ad assestarsi su un valore stabile in seguito a una rapida variazione della grandezza in esame. La prontezza dipende dai fenomeni fisici che stanno alla base del funzionamento dello strumento. Tutti sappiamo che, per esempio, un termometro clinico impiega qualche minuto per misurare la temperatura corporea: si tratta di uno strumento di prontezza piuttosto bassa, e sarebbe ben poco affidabile se dovessimo impiegarlo per misurare una temperatura che varia in modo rapido. Invece una bilancia digitale risponde in maniera veloce a variazioni della massa che deve misurare: si tratta di uno strumento dotato di una buona prontezza.
Ripetibilità: corrisponde alla capacità dello strumento di fornire misure uguali della stessa grandezza entro la sua precisione, anche in condizioni di lavoro difficili o variabili (vibrazioni, sbalzi di temperatura, ecc.)

Esempio:

Consideriamo lo strumento riportato nella figura seguente chiamato “amperometro”, che misura la grandezza fisica chiamata “intensità di corrente elettrica” (l’unità di misura è l’Ampere che ha come simbolo: A)

La sua portata è ovviamente 12 A. Per calcolare la risoluzione osserviamo che nella scala ci sono in totale 60 divisioni; attenzione a non confondere le divisioni con le incisioni (o tacche)! Le divisioni sono le spaziature tra una incisione e l’altra! In questo strumento le divisioni sono 60 mentre le incisioni sono 61. Quindi la risoluzione sarà:

risoluzione = portata / n° totale divisioni = 12 / 60 = 0,2 A/divisione.

Che sta a significare che una divisione vale 0,2 A
Spieghiamo meglio il concetto: supponiamo che l’indice non sia nella posizione indicata nella figura ma in corrispondenza del numero 4; lo strumento sta misurando un valore di 4 A di corrente. Supponiamo ora che la corrente aumenti di 0,2 A: lo strumento si porterà nel segno successivo a quello corrispondente il numero 4 e leggeremo pertanto 4,2 A. Ma se la corrente fosse aumentata di meno di 0,2 A, per esempio di 0,05 A (quindi di un quarto del valore di una divisione), l’indice si sarebbe spostato ma di poco restando vicino al segno corrispondente al valore 4 A e pertanto lo strumento non sarebbe stato in grado di rilevare la differenza tra il valore 4 A di prima e il nuovo valore 4,05 A. Ecco perché si dice che la risoluzione (in questo caso di 0,2 A) è la variazione minima della grandezza che lo strumento è in grado di rilevare; nel nostro caso dallo strumento non riusciamo a rilevare una differenza nel valore letto se la grandezza varia di meno di 0,2 A.

La sensibilità, invece, poiché corrisponde all’inverso della risoluzione, varrà:

1/0,2 = 5 divisioni/A
che sta a significare che quando lo strumento misura 1 A l’indice si sposta di 5 divisioni (come si può facilmente capire anche dalla figura)

Notiamo una cosa importante: per calcolare la risoluzione non è necessario sempre usare tutte le divisioni della scala; a volte contarle tutte può essere lungo e può portare a errori nel conteggio. Basta infatti prendere solo una porzione dell’intera scala e dividere il valore corrispondente all’ultima incisione con il numero di divisioni di questa porzione di scala. Nel nostro esempio, avremmo potuto prendere metà scala; essa è divisa in 30 parti e va a finire nel valore 6 A, facendo il rapporto 6 / 30 si ottiene sempre il valore di 0,2 A/divisioni.
Poiché allora ogni divisione della scala corrisponde a 0,2 A, il valore letto dallo strumento in figura risulta di 4,6 A.

Esercizio per casa: osservate gli strumenti che avete in casa, ad esempio metro, righello, termometro, barometro, cronometro, bilancia da cucina, bilancia pesapersone, contatore dell’energia elettrica, contatore del gas, contatore dell’acqua, contachilometri dell’auto, tachimetro dell’auto (cioè quello che misura la velocità) . Di ognuno leggete la sensibilità, la risoluzione e il fondo scala.

VALUTAZIONE DELL’INCERTEZZA IN UNA SINGOLA MISURA DIRETTA

Valutazione dell’incertezza nella lettura di scale

Supponiamo di voler misurare la lunghezza L di una penna utilizzando una riga che ha le incisioni separate le une dalle altre di 1 centimetro. A questo scopo cercheremo di far coincidere lo zero del metro con l’inizio della penna e dovremo valutare in quale posizione della scala va a finire la sua punta. Supponiamo di ottenere la situazione rappresentata in figura:

Quale valore ritieni si debba riportare come valore della grandezza L? La punta della penna appare essere un po’ dopo la metà tra 6 cm e 7 cm quindi si potrebbe essere tentati ti azzardare a occhio i valori 6,6 cm o 6,7 cm o anche 6,8 cm. Riportare però tali valori non è corretto perché lo strumento adoperato, per come è stato costruito, non consente di effettuare letture intermedie tra 6 cm e 7 cm. Nessuno, valutando a occhio, può stabilire con certezza se la lunghezza L della penna vale effettivamente 6,6 cm o 6,7 o, tanto meno, 6,55 cm o 6,723 cm o 6,675 cm…Non possiamo dire dei numeri a caso! Non dimentichiamo infatti che il risultato di una misura deve essere oggettivo, cioè deve essere lo stesso indipendentemente da chi effettua la misura.

Allora, che cosa potrebbero sicuramente dire tutti gli sperimentatori di fronte alla situazione rappresentata in figura? Senza dubbio tutti concorderanno sul fatto che la lunghezza L della penna è un valore compreso tra 6 cm e 7 cm, cioè:

6 cm < L < 7 cm

Ma qual è la miglior stima di L sulla quale tutti possono essere d’accordo? Cioè, qual è quel valore che approssima meglio il valore di L e che direbbero tutti senza azzardare valori a caso tipo 6,6 o 6,7 o 6,68 ecc.. i quali inevitabilmente sarebbero diversi da operatore a operatore? Dalla figura tutti gli sperimentatori saranno d’accordo sul fatto che la punta della penna finisce più vicina alla metà tra 6 cm e 7 cm (quindi a 6,5 cm) piuttosto che a 6 cm o a 7 cm. In questo caso, infatti, non siamo in grado di dividere a occhio una divisione di 1 cm in dieci parti (ed è per questo che non possiamo dare valori tipo 6,6 cm o 6,7 cm), ma siamo certamente in grado di valutare se l’estremità di un certo oggetto cade più vicina al primo estremo della divisione o al secondo estremo o al punto di mezzo (si dice in questo caso che siamo in grado di apprezzare la mezza divisione). Per cui prenderemo come valore più attendibile di L il valore 6,5 cm.

Allora, per concludere, se vogliamo comunicare il risultato della nostra misurazione, dovremo fornire due elementi:

Il valore della grandezza che ci sembra più attendibile, cioè quello che riteniamo essere il valore più vicino a quello esatto, vero, effettivo, senza però sparare a caso misure sulle quali diversi osservatori potrebbero essere in disaccordo. Tale valore in questo caso sarà 6,5 cm.
Ma comunicare solamente il valore 6,5 cm non basta. Infatti il valore esatto di L non sarà esattamente 6,5 cioè 6,50000000…. con infiniti zeri dopo il 5. Potrà essere 6,5582 cm oppure 6,61342 o altri infiniti possibili valori, nessuno lo potrà mai sapere utilizzando tale strumento. Dovremo fornire pertanto un intervallo di valori all’interno del quale siamo ragionevolmente certi che stia il valore esatto di L: in questo caso prenderemo tale intervallo quello che va da 6 cm a 7 cm.

Per comunicare questi due concetti, il risultato di una misura si scrive con la seguente notazione:

Che sta a indicare proprio che il valore che riteniamo sia più attendibile per L è 6,5 cm e riteniamo che il valore esatto (detto anche valore vero) di L, che non conosciamo e che non si potrà mai conoscere, sia compreso nell’intervallo tra 6,5 – 0,5 = 6 cm 6,5 + 0,5 = 7 cm. Tale intervallo viene chiamato intervallo di indeterminazione o di confidenza (appunto per indicare che si è ragionevolmente confidenti che il valore esatto della grandezza sia uno di quegli infiniti valori che stanno dentro questo intervallo),

Il tutto è schematizzato nella seguente figura:

Come vi sarete accorti, la nostra misura è molto rozza, nel senso che l’intervallo di indeterminazione tra 6 cm e 7 cm è molto ampio per il valore della lunghezza di una penna. Possiamo ovviamente fare molto meglio, basterà usare una riga con una risoluzione minore, per esempio di 1 mm. Il tutto è mostrato in figura.

Come scriveremo in questo caso il risultato della misura? Se più sperimentatori osservano attentamente la situazione, alcuni potranno dire che la punta della penna si trova un po’ prima di 6,7 cm e altri un po’ dopo 6,7 cm, ma nessuno riuscirà a quantificare questo scarto da 6,7 cm. Il massimo su cui tutti possono essere d’accordo è il fatto che l’incisione più vicina alla punta della penna è quella corrispondente al valore 6,7 cm e che il valore L della penna sarà compreso tra 6,6 cm e 6,8 cm.

Notiamo che in questo caso, a differenza di quello precedente, essendo le divisioni molto vicine tra loro, risulta molto difficile apprezzare la mezza divisione, ossia il mezzo millimetro. Cioè, se l’estremità di un certo oggetto cade tra due tacche spaziate tra loro di 1 mm, è difficile stabilire se tale estremità è più vicina alla prima tacca, alla seconda o alla metà tra le due; si riesce solamente a distinguere se è più vicina alla prima tacca o alla seconda. Quindi, in questi casi, anche se l’oggetto cade approssimativamente a metà tra due incisioni, si preferisce attribuire alla misura il valore corrispondente alla prima tacca o quello corrispondente alla seconda tacca, in base a quale di esse è ritenuta più vicina. Per quanto riguarda l’incertezza assoluta, in questi casi si conviene prenderla uguale al valore di una divisione, ossia alla risoluzione dello strumento.

Quindi il risultato della nostra misurazione sarà:

L = (6,7 ± 0,1) cm

Consideriamo ora il caso in cui si voglia misurare con una riga millimetrata la lunghezza di un oggetto di forma rettangolare e senza “sbavature” all’estremità. Supponiamo ora che, a differenza dei casi precedenti in cui l’estremità finale dell’oggetto cadeva tra due incisioni, qui l’estremità dell’oggetto cada esattamente su una incisione della riga. Il tutto è mostrato in figura.

In questo caso si potrebbe erroneamente pensare di scrivere come risultato della misura: L = 4,2 cm senza nessun margine di incertezza, visto che non abbiamo dubbi sul fatto che l’estremità finale dell’oggetto cade “esattamente” sulla seconda incisione dopo 4 cm. Ma pensiamoci un attimo, possiamo essere sicuri che il valore esatto di L sia esattamente 4,2000000…..con infiniti zeri dopo il 2? Ovviamente no, lo strumento non riesce a fornirci ulteriori cifre dopo il 2 ed è impensabile poter affermare che la lunghezza effettiva dell’oggetto sia 4,21 piuttosto che 4,19 o 4,2203 o 4,195. Lo strumento non riesce a distinguere lunghezze che differiscono tra loro meno del millimetro; a riprova di ciò basta pensare di applicare sull’estremo dell’oggetto uno strato di scotch e di ripetere la misurazione: è chiaro che vedremo sempre l’estremità dell’oggetto finire sulla stessa incisione di prima anche se la lunghezza dell’oggetto è cambiata! Per fare un altro esempio di questo tipo pensiamo di pesarci su una bilancia avente una risoluzione di 0,5 kg e di leggere 62,0 kg: non possiamo sapere se il valore effettivo della nostra massa sia 62,1 o 61,9 perché la bilancia non è in grado di apprezzare i decimi di kg; a riprova di ciò se si prende una mela in mano e ci si rimette sopra vedremo che l’indice praticamente non si è spostato.

Non scordiamoci inoltre che la tacca stessa ha un certo spessore (vedi ingrandimento nella stessa figura), per cui, se per esempio fosse di 0,05 mm, per oggetti di lunghezze diverse ma che differiscono tra loro meno di 0,05 mm, il nostro occhio vedrebbe la loro estremità coincidere sempre sulla stessa tacca.

Un’ulteriore causa che rende incerta la nostra misura è il fatto che non possiamo essere sicuri di aver allineato esattamente la prima estremità dell’oggetto (quella di sinistra in figura) con lo zero della riga.

Infine, un’altra fonte di incertezza sul valore misurato riguarda il fatto che non siamo sicuri che tutte le divisioni della riga siano spaziate esattamente di quella quantità che universalmente viene accettata come millimetro, cioè esattamente come la milionesima parte dell’unità di misura campione di lunghezza che è il metro. Per capire meglio questo discorso, supponiamo di disporre idealmente di una riga “perfetta” in cui l’ampiezza di tutte le divisioni sia esattamente 1 mm. L’ampiezza delle divisioni di questa riga non sarà identica a quella della riga usata da noi e quindi l’estremità dell’oggetto da misurare cadrà stavolta in una posizione differente rispetto alla tacca 4,2 cm. Se facciamo un ingrandimento della zona in cui l’oggetto finisce, la situazione potrebbe essere per esempio quella mostrata in figura:

Se fosse quella di figura la situazione, capiamo che la misura esatta della lunghezza L dell’oggetto è un po’ meno di 4,2 cm, anche se non possiamo valutare quanto.

Concludiamo quindi che anche nel caso in cui l’estremità di un oggetto va a finire esattamente su un’incisione della scala, la misura sarà sempre affetta da una certa incertezza, perché:

ogni strumento concretamente fabbricabile avrà una scala che, per quanto fine, non si può legger con precisione infinita (chi ce lo dice che la lunghezza L del nostro oggetto non possa avere una lunghezza L pari a 4,200001 cm?). A causa di ciò qualunque valore più piccolo della risoluzione dello strumento non può essere letto, e quindi non può essere dato con certezza. Questa incertezza è detta incertezza di risoluzione dello strumento
L’allineamento dell’oggetto con lo zero della scala non sarà mai perfetto, cioè noi non avremo allineato con esattezza assoluta lo zero della scala con l’inizio dell’oggetto. E questo vale anche per gli strumenti dove si muove un indice su una scala. Questi strumenti hanno un dispositivo per portare l’indice sullo zero della scala quando lo strumento non misura niente (in questo caso si tratta sempre di un allineamento perché si allinea lo zero della scala con il valore zero della grandezza) ma tale azzeramento a mano non sarà mai perfetto. Questa incertezza è detta incertezza di allineamento tra la grandezza e lo strumento
Lo strumento non riuscirà a riprodurre l’unità di misura, i suoi multipli o sottomultipli in maniera assolutamente perfetta (nella nostra riga le divisioni non possono essere spaziate esattamente di 1 mm l’una dall’altra). Cioè lo strumento potrà fornire un’unità di misura che sarà molto simile, ma non potrà essere assolutamente uguale a quella campione accettata a livello internazionale. Questa incertezza è detta incertezza di calibrazione o di taratura dello strumento.

Un’ultima considerazione che dobbiamo fare riguarda la scrittura di misure un po’ particolari. In figura sono mostrati due oggetti che chiamiamo oggetto 1 e oggetto 2 le cui lunghezze rispettivamente L₁ e L₂ vengono misurate utilizzando due righe con risoluzioni differenti.

Come scriveremmo i risultati di ciascuna misura?

Non si scrive

L₁ = (3 ± 0,5) cm e L₂ = (5 ± 0,1) cm

Bensì:

L₁ = (3,0 ± 0,5) cm e L₂ = (5,0 ± 0,1) cm

Cioè va riportato anche lo zero finale. Infatti, anche se 5 è equivalente numericamente a 5,0 quando si ha a che fare con misurazioni i due valori forniscono informazioni differenti: scrivendo 5,0 si vuole affermare una conoscenza anche della cifra dopo il 5, cioè che lo strumento riesce a misurare anche la cifra dopo il 5.

Valutazione dell’incertezza nella lettura di strumenti digitali

Un discorso analogo a quello che abbiamo fatto vale nel caso in cui effettuiamo una misurazione con uno strumento digitale. Supponiamo per esempio di avere un timer digitale che misura, mediante un sistema elettronico, il tempo impiegato da un atleta a percorrere 100 m. L’orologio parte quando avviene lo sparo e si ferma quando l’atleta sorpassa una fotocellula posta sul traguardo. Supponiamo che il display fornisca il seguente risultato in secondi.

Ci chiediamo: avrà un’incertezza questo risultato? Certo che l’avrà. Ci sarà un’incertezza di risoluzione dovuta al fatto che lo strumento non è in grado di misurare i millesimi di secondo; la misura esatta del tempo potrebbe essere 10,031 oppure 10,029 oppure altri infiniti possibili valori, e lo strumento non è in grado di dirmelo. Poi ci sarà un’incertezza di calibrazione, in quanto la durata del millisecondo dello strumento sarà molto simile ma non sarà esattamente uguale alla durata del millisecondo battuta da un orologio atomico.

Nel caso degli strumenti digitali, per tener conto quindi di tutte queste cause di incertezza, si è soliti prendere come incertezza assoluta da associare al risultato il valore corrispondente alla risoluzione dello strumento. Quindi, nel nostro caso particolare, scriveremo il risultato della misurazione come:

t = (10,03 ± 0,01) s

È possibile effettuare una misura “esatta”?

Dalle considerazioni fatte fino a questo momento dovrebbe essere chiaro che con nessuno strumento, neanche il più preciso e sofisticato esistente, si riuscirà mai a sapere il valore esatto di una qualsiasi grandezza fisica. Quindi ci si deve abituare all’idea che il risultato di un’operazione di misurazione non può mai produrre un valore numerico infinitamente preciso (cioè con infinite cifre, come lo sono i numeri trattati in matematica), bensì un intervallo di valori. Tale considerazione non è legata ad azioni sbagliate effettuate da parte dell’operatore, ma è dovuta al fatto che la misurazione, essendo eseguita con dispositivi reali, non può per sua natura portare a un risultato, per così dire, perfetto. Operando con cura, possiamo essere capaci di ridurre le incertezza finché sono estremamente piccole, ma eliminarle del tutto è impossibile.

Facciamo un esempio che illustra questo concetto. Se misuriamo la lunghezza di un certo oggetto con strumenti via via più sensibili, possiamo ottenere per esempio la situazione rappresentata in figura (per i primi 3 strumenti, essendo le tacche molto distanziate tra loro, abbiamo preso come incertezza assoluta il valore di mezza divisione, mentre per l’ultimo strumento abbiamo preso come incertezza assoluta il valore di un’intera divisione):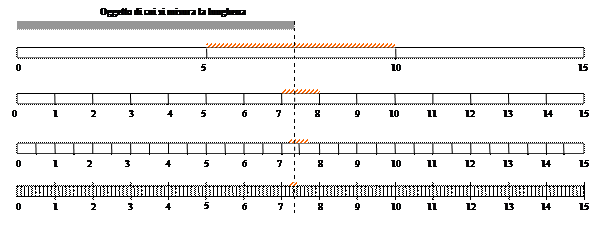

Con il disegno non si può andare oltre al quarto strumento perché non è più possibile disegnare uno strumento con una risoluzione minore: gli intervalli fra due tacche successive avrebbero praticamente le stesse dimensioni delle tacche e non si distinguerebbero più. Possiamo, però, fare un esperimento ideale, cioè un esperimento che possiamo pensare, ma che nella realtà non può essere eseguito. Possiamo pensare di costruire altri strumenti con una risoluzione sempre più piccola, e di leggere la misura con un’incertezza sempre più piccola (per ora il metodo più preciso per la misura di lunghezze utilizza un interferometro laser, il quale ha una risoluzione di circa 0,5 · 10^–6 m) . È chiaro che questo esperimento ideale può proseguire all’infinito, senza che si riesca ad arrivare a un valore esatto della misura. Perciò, anche gli scienziati, usando strumenti molto sofisticati e costosi, fanno misure sempre e soltanto approssimate. Certo, le fanno molto più precise di quanto possiamo farle noi, cioè riescono a misurare molte più cifre di quanto possiamo misurarne noi, ma comunque non possono assolutamente raggiungere l’esattezza assoluta.

Nelle misure di ogni giorno in genere non ci preoccupiamo di discutere delle incertezze semplicemente perché non ci interessano. Se diciamo che la distanza Urbino – Pesaro è 36 km, non importa (nella maggior parte dei casi) se questo significa “compresa tra 35,5 e 36,5 km” oppure “compresa tra 35,9 e 36,1 km”. Eppure, anche nella vita quotidiana, se ci pensiamo, l’incertezza associata a una misura ha la sua importanza. Se il negoziante ci dà venti grammi in più di prosciutto in più rispetto a quanto gli avevamo chiesto non ci scandalizziamo, ma certo non tollereremo che in una pillola ci fossero venti grammi di antibiotico più del dovuto! Ci sono però delle situazioni in cui una maggiore o minore incertezza della misura può fare la differenza. Se ad esempio su una strada rettilinea c’è il limite di velocità di 90 km/h, un’auto che viaggia esattamente a 90 km/h non commette infrazione. Supponiamo ora che una pattuglia della polizia stradale riveli con l’autovelox che una macchina sta andando di poco sopra i 90 km/h: quell’automobilista deve essere multato oppure no? La misura avrà la sua incertezza, quindi potremo avere una lettura dell’autovelox superiore a 90 km/h e tuttavia compatibile con una velocità inferiore al limite. Per questo motivo la legge ammette una tolleranza del 5% sulla velocità rivelata, con un minimo di 5 km/h per velocità rilevate fino a 100 km/h prima di far scattare la sanzione. Vediamo allora che in questo caso una maggiore o minore incertezza può fare la differenza…di qualche centinaio di euro di multa!

Inoltre nella vita quotidiana vengono presentate spesso misure senza esplicitare l’incertezza assoluta; questo succede per i prodotti commerciali e per molti dati tecnici, come le caratteristiche degli elettrodomestici e dei veicoli. Questo non perché tali valori siano esatti, ma perché l’indicazione dell’incertezza non ha una rilevante importanza pratica. Per esempio, a noi non importa molto se una lampadina consuma 100 W oppure 101 W.

Infine, osserviamo che nell’insegnamento di laboratorio nella scuola, a volte si misurano grandezze (come per esempio c, la velocità della luce, o e, la carica dell’elettrone) che sono state accuratamente misurate molte altre volte in precedenza, e per le quali vi è un “valore accettato” molto accurato che è noto e pubblicato sui libri. Questo valore accettato, naturalmente, non è esatto, anche se qualche lettore potrebbe essere ingannato dal fatto che nel suo libro non è riportata l’incertezza. Esso è il risultato di misure e, come i risultati di qualsiasi misura, è affetto da una certa incertezza. Nondimeno, esso è molto più accurato di quello che lo studente può raggiungere da solo e la sua incertezza è estremamente piccola rispetto a quella che si può ottenere nella maggior parte dei laboratori didattici. Per esempio, il valore correntemente accettato di c, la velocità della luce è c_accettato = (299792458 ± 1) m/s.

Concludiamo dicendo che se finora pensavate che la Fisica e le altre scienze sperimentali fossero delle scienze esatte, dovete cambiare idea. Tutte le scienze sperimentali sono approssimate! Una parte del progresso scientifico consiste proprio nel riuscire a effettuare misure sempre più precise, Talvolta passano parecchi decenni prima che si riesca ad aggiungere una sola cifra a una certa misura. E talvolta questo miglioramento della precisione fornisce risultati che mettono in crisi teorie scientifiche che sono state accettate per secoli!

Misure scritte in notazione esponenziale

Le misure possono essere scritte anche in forma esponenziale, forma che risulta più comoda quando si ha a che fare con numeri molto grandi o molto piccoli. Per comodità di scrittura poi, l’esponente si può scrivere dopo la parentesi. Facciamo alcuni esempi per chiarire meglio.

Se con un esperimento abbiamo misurato al carica di un elettrone e abbiamo ottenuto il risultato 1,61 · 10^–19 C con un’incertezza di 5 · 10^–21 C, invece di scrivere: (1,61 · 10^-19 ± 5 · 10^-21) C è più comodo portare il risultato e l’incertezza con la stessa potenza di 10 e scrivere: (1,61 ± 0,05) · 10^-19 C. A differenza della prima scrittura, da quest’ultima è immediato contare il numero di cifre significative (vedi paragrafo: Cifre significative di una misura”), in questo caso tre, e calcolare l’incertezza relativa (vedi paragrafo: incertezza assoluta, relativa, percentuale) perché basta fare il rapporto tra 0,05 e 1,61 non considerando gli esponenti poiché essi risultano uguali sia per il risultato che per l’incertezza relativa e quindi nel rapporto si semplificano.

Per fare un altro esempio, supponiamo di aver misurato una massa di 3,156 · 10³⁴kg con un’incertezza di 10³¹ kg; invece di scrivere (3,156 · 10³⁴ ± 10³¹) kg è meglio scrivere (3156 ± 1) · 10³¹ kg.

Riassunto

Quando effettuiamo una singola misura diretta di una determinata grandezza fisica con uno strumento di misura non possiamo mai ottenere il valore esatto della grandezza perché:
Ogni strumento avrà una risoluzione che, per quanto piccola, non potrà mai essere zero (cioè lo strumento non ci potrà mai fornire infinite cifre)
L’allineamento tra la grandezza e lo zero dello strumento non potrà mai essere perfetto
Lo strumento non riuscirà a riprodurre l’unità di misura, i suoi multipli o sottomultipli in maniera assolutamente perfetta
Quindi quando effettuiamo una misura, oltre al valore misurato dovremo fornire un intervallo di valori. Con l’indicazione di tale intervallo noi vogliamo dire che siamo ragionevolmente certi che il valore esatto della grandezza (che sarà sempre un valore sconosciuto) sia uno di quegli infiniti valori compresi nell’intervallo stesso.
Il risultato di una singola misura diretta lo scriveremo quindi come:
simbolo della grandezza misurata = (valore misurato ± incertezza assoluta) unità di misura
L’intervallo che va da (valore misurato – incertezza assoluta) a (valore misurato + incertezza assoluta) si chiama intervallo di indeterminazione
Quando si effettua una singola misura diretta con uno strumento analogico, se le tacche sono molto distanziate tra loro l’incertezza assoluta si prende uguale a metà del valore della risoluzione dello strumento, mentre se le tacche sono molto ravvicinate si prende uguale al valore della sensibilità. Per gli strumenti digitali si è soliti prendere come incertezza assoluta il valore della risoluzione dello strumento.
In questi casi l’incertezza assoluta dipende da come è fatto lo strumento ed è per questo che si dice che l’incertezza assoluta è di tipo strumentale. È chiaro quindi che l’intervallo di indeterminazione sarà tanto più piccolo quanto più lo strumento è preciso, cioè quanto più la sua risoluzione è piccola.

Fonte: http://www.webalice.it/paolocesaretti/appunti/misura.doc

Sito web da visitare: http://www.webalice.it/paolocesaretti/

Autore del testo: non indicato nel documento di origine

Parola chiave google : Incertezza ed errori di misura tipo file : doc

Incertezza ed errori di misura

Tipologie di errori

Accidentali à Avvengono in entrambi i sensi e dipendono da piccoli cambiamenti

delle condizioni in cui si esegue l’esperimento.

Sistematici à Avvengono sempre in un senso, derivano da deficienze strumentali o

da metodi di misurazione errati

Nel caso di misure ripetute (supponiamo N) della stessa grandezza fisica x utilizzando lo stesso strumento di misura è probabile ottenere dei numeri che differiscono l’uno dall’altro per meno dell’errore di sensibilità dello strumento.

In effetti questo non succede sempre perché si commettono degli errori accidentali nell’atto di misura e così l’errore complessivo può dunque essere più grande dell’errore di sensibilità dello strumento.

Teoria degli errori à Consente di calcolare il valore più attendibile delle misure di una

grandezza e l’incertezza che lo accompagna quando si abbiano solo

errori accidentali.

Fonte: http://www.visus.altervista.org/files/Integrazione%20GrandezzeFisicheMisure.doc

Autore del testo: non indicato nel documento di origine

Parola chiave google : Incertezza ed errori di misura tipo file : doc

MISURE DELLE GRANDEZZE

Il problema della misura delle grandezze si pone quando vogliamo fare un’osservazione SCIENTIFICA nello studio di un sistema, di un corpo, di un fenomeno.

SISTEMA: un oggetto complesso considerato, nelle sue diverse componenti, come fosse unico.

Ex. il sistema “automobile”; il sistema “Pianeta Terra”; ecc.

CORPO: porzione di materia che può avere forma definita e che viene presa in considerazione nella sua interezza.

Ex. Una pallina da tennis, una penna, un orologio, un sasso, ecc.

PUNTO MATERIALE: un oggetto considerato in una situazione in cui è possibile trascurarne le dimensioni.

Ex. una macchina che corre lungo un’autostrada o una città rappresentata nella carta geografica.

GRANDEZZE: tutte le proprietà di un corpo, di un sistema, di un punto materiale o di un fenomeno che possono essere misurate.

MISURARE: Significa confrontare una grandezza ignota (da misurare) con una grandezza nota detta unità di misura e vedere quante volte la grandezza in esame contiene l’unità di misura. In pratica consiste nel fare il rapporto tra la grandezza da misurare e l’unità di misura.

Ex. Se misuro una distanza di 2 metri usando un’unità di misura da 1metro, posso affermare che:

grandezza da misurare / unità di misura = 2 m / 1 m = 2.

L’unità di misura da 1 m sta 2 volte nella grandezza da misurare.

Per poter misurare occorre:

una grandezza da misurare;
un’unità di misura;
uno strumento di misura.

Le grandezze misurate, ad esempio la massa, si indicano così:

m = 2 kg

m = simbolo della grandezza; 2 = valore numerico; kg = unità di misura.

UNITÀ DI MISURA. Le unità di misura sono arbitrarie. Nella storia dell’uomo ne sono state usate molte; la maggior parte di esse era di tipo soggettivo: le “braccia”, le “spanne”, ecc. nel caso della misura della lunghezza.

Affinché una misura sia “trasferibile” e quindi “accettabile” per altri, deve essere di tipo oggettivo.

Affinché una misura sia accettabile in tutto il mondo e per uniformare la “selva” di unità di misura è stato istituito, nel 1960, il Sistema Internazionale di misura (SI) che definisce un’unità di misura per ogni grandezza.

Le grandezze si dividono in:

FONDAMENTALI, se non dipendono da nessun’altra grandezza;
DERIVATE, se dipendono da altre grandezze.

Ex. Mentre la massa è una grandezza fondamentale che non dipende da nessuna altra grandezza, il peso è una grandezza derivata, perchè dipende dalla massa e dall’accelerazione di gravità: P = m x g.

Dal punto di vista operativo le misure possono essere di tipo diretto o di tipo indiretto.

MISURE INDIRETTE. Vengono effettuate tramite calcoli matematici, basate su procedimenti geometrici. Questi calcoli possono essere fatti dalle persone, oppure da appositi strumenti, più o meno sofisticati, che restituiscono direttamente la misura indiretta.

Ex. si può misurare l’area del quadrato con la formula (lato x lato), la distanza di un punto inaccessibile con il metodo della parallasse e delle triangolazioni...il sonar, il radar, l’ecoscandaglio, il tacheometro ed altri.

STRUMENTI DI MISURA. Gli strumenti sono delle macchine od oggetti opportunamente tarati, usati per misurare.

TARATURA: è un procedimento che serve a far corrispondere le indicazioni

di uno strumento con i valori delle grandezze che vogliamo misurare.

TIPOLOGIA: possono essere di tipo analogico se dotati di scale graduate,

oppure di tipo digitale, se dotati di display.

INTERVALLO DI MISURA: la misura da verificare deve “cadere” in un

intervallo di grandezza appropriato per lo strumento.

Ex. non posso misurare la lunghezza di una strada di 10 km con un calibro o con un metro da sarto.

PORTATA: è il massimo valore che può misurare uno strumento.

PRONTEZZA: è il tempo necessario allo strumento per fornire la misura.

Ex. Il termometro clinico a mercurio impiega 4-5 minuti per misurare la febbre.

SENSIBILITÀ: è il più piccolo intervallo di misura (valore) della grandezza

da misurare, rilevabile con un determinato strumento.

Ex. la sensibilità del righello è pari a 1 mm; quella del metro da sarto e pari a 1 cm; quella del calibro decimale è pari a 0,1 mm, nella vite micrometrica di Palmer è pari a 0,01 mm.

Non si possono rilevare valori di misura inferiori alla sensibilità dello strumento usato.

INCERTEZZA. Per quanto una misura possa essere accurata c’è sempre uno scostamento tra il dato misurato ed il vero valore della grandezza. Tale valore è l’incertezza della misura.

Nella migliore delle ipotesi l’incertezza di una misura coincide con

l’incertezza dello strumento;

L’incertezza si manifesta sempre in caso di misurazioni effettuate da più

individui.

In una misurazione l’incertezza deve essere sempre indicata; essa ci indicherà anche la sensibilità dello strumento usato.

Ex. se si misura una lunghezza di 10 cm con il metro da sarto che ha una sensibilità pari a 1 cm, devo scrivere l = (10 ± 1) cm; se si misura la stessa con il righello che ha una sensibilità pari a 1 mm, la stessa si scriverà l = (100 ± 1) mm.

ERRORI DI MISURA. Ogni volta che si misura si commettono inevitabilmente degli errori, che contribuiscono all’incertezza della misurazione rilevata. Tali errori, in base alla loro natura ed a come si propagano, nel caso di misurazioni ripetute o consecutive, si dividono in errori sistematici ed errori casuali o accidentali.

ERRORI SISTEMATICI. Si chiamano così perché si ripetono sistematicamente ad ogni misurazione, sempre con lo stesso segno. La loro natura è nota e possono essere, entro certi limiti, eliminati o ridotti al minimo. Essi dipendono da varie cause:

IMPERFEZIONI STRUMENTALI. Se lo strumento non è ben costruito,

oppure è difettoso o danneggiato e quindi non funziona correttamente;

USO ERRATO DELLO STRUMENTO. In una misurazione di una lunghezza

effettuata con il righello, potrebbe verificarsi il caso di un operatore che inizia la lettura a partire dal bordo della righello anziché dallo zero della scala;

METODO ERRATO. Il procedimento di misura non è corretto. Ad esempio

volendo misurare il tempo di caduta di un grave, l’operatore si posiziona in cima ad una torre, lascia cadere il grave accendendo il cronometro, per poi arrestarlo al momento che sente il tonfo dell’urto del grave al suolo. Questo procedimento è viziato da errore perché non tiene conto del tempo impiegato dal suono per raggiungere l’operatore che deve fermare il cronometro;

ERRORI DI LETTURA. Quando, all’atto della lettura di una scala graduata,

l’operatore, anziché porsi in posizione perpendicolare alla suddetta scala, si pone in una posizione non corretta, commettendo un errore di parallasse.

ERRORI CASUALI O ACCIDENTALI. Sono errori di natura sconosciuta, dovuti a cause ignote, sono difficilmente rilevabili e non si ripetono mai con lo stesso segno. Perciò si cerca di ridurli al minimo attraverso la teoria degli errori.

TEORIA DEGLI ERRORI.

Secondo questa teoria gli errori possono essere assoluti e relativi. Trattandosi di situazioni che determinano incertezza nelle misurazioni, parleremo d’incertezza assoluta e d’incertezza relativa.

INCERTEZZA ASSOLUTA. E’ insita in tutte le misure e deriva essenzialmente dalla sensibilità dello strumento e dalla presenza di errori di misura. Minore sarà l’incertezza assoluta e più accurata risulterà la misurazione, per cui, ogni volta che si effettua una misura, si dovrà sempre indicare l’incertezza da cui è affetta:

l = X ± Y m

in cui l = lunghezza; X = valore numerico della misura e Y = valore dell’incertezza assoluta. La misura esatta sarà compresa tra (X ─ Y) e (X + Y).

Ritornando all’esempio della distanza di 10 cm misurata con il metro da sarto, essa corrisponde a l = (10 ± 1) cm; si può affermare che la distanza esatta è compresa tra l = (10 – 1) cm = 9 cm e l = (10 + 1) cm = 11 cm, con un’incertezza assoluta pari a ± 1 cm. La stessa, misurata con il righello, corrisponderebbe a

l = (100 ± 1) mm,

con una misura esatta compresa tra l = (100 – 1) mm = 99 mm e l = (100 + 1) mm = 101 mm, con un’incertezza assoluta di ± 1 mm.

Nel caso di misurazioni ripetute n volte, posso dividere la sommatoria dei valori riscontrati per “n”, ottenendo un Valore Medio “VM”. Tale valore medio corrisponde al più probabile valore esatto della misura.

Ex. Misurati i seguenti valori di lunghezza espressi in cm: 15,3; 15,4; 15,2; 15,5; 15,6. Si fa la sommatoria: 15,3 + 15,4 + 15,2 + 15,5 + 15,6 = 77,0 cm e poi

77 / 5 = 15,4 cm (VM) Valore Medio.

Sommando il valore massimo con il valore minimo e dividendo il risultato per due, si ottiene la semidispersione massima che, nel caso di misurazioni ripetute, corrisponde all’incertezza assoluta e si esprime con la stessa unità di misura del valore rilevato.

Nell’esempio sopra citato avremo:

(15,6 ─ 15,2) cm / 2 = 0,4 / 2 = 0,2 cm incertezza assoluta.

La misura effettuata corrisponderà al VM ± l’incertezza assoluta:

l = (15,4 ± 0,2) cm

INCERTEZZA RELATIVA. Talvolta si rende necessario quantificare l’incertezza di una misurazione, per verificarne l’accuratezza e per poterla confrontare con altre misurazioni. Per fare ciò occorre calcolare l’incertezza relativa che corrisponde al rapporto tra l’incertezza assoluta ed il valore medio:

Incertezza assoluta / Valore Medio = Incertezza Relativa (IR)

Nel caso di cui sopra avremo:

IR = 0,2 cm / 15,4 cm = 0,013

Poiché nel rapporto le unità di misura si annullano, il numero che ne deriva è un numero adimensionale, privo di unità di misura; ciò significa che l’incertezza relativa è un numero puro che si può esprimere in percentuale e permette il confronto fra tutte le possibili misurazioni.

Ex. Dovendo confrontare la misura l₁ = (250 ± 5) m e la misura l₂ = (10 ± 1) cm, basta calcolare l’incertezza relativa e avremo:

l₁ = (5 / 250) m = 0,02 = 2% mentre l₂ = (1 / 10) cm = 0,1 = 10%.

Poiché 0,1 > 0,02, la misura l₁ (2% d’incertezza) è molto più accurata della misura l₂ (10% d’incertezza) nonostante quest’ultima avesse un‘incertezza assoluta di 1 cm contro l’incertezza di 5 m della prima.

CIFRE SIGNIFICATIVE. Sono quelle cifre che compongono il valore numerico di una misura e che hanno un significato ai fini della misura; esse dipendono dalla sensibilità dello strumento utilizzato.

Ex. Se si rileva una lunghezza l = 2 m, abbiamo una sola cifra significativa e vuole dire che tale misura è stata rilevata con uno strumento di sensibilità pari 1 m, per cui la misura si scriverà l = (2 ± 1) m.

Se si rileva la stessa con uno strumento della sensibilità di 1 cm, la misura si scrive l = (2,0 ± 0,1) m. Lo zero dopo la virgola è significativo e non può essere eliminato perchè indica la sensibilità dello strumento usato. Analogamente se la sensibilità è di 1 mm, la misura si scrive l = (2,00 ± 0,01) m, con due zeri significativi.

Non si può scrivere l = 2,0 m se la misura è stata rilevata con uno strumento dotato di sensibilità pari a 1 m, quindi lo zero dopo la virgola non è significativo.

I campioni di riferimento delle unità di misura depositati in appositi musei o in laboratori specifici raggiungono 10 cifre significative, mentre nei laboratori comuni si arriva al massimo a 4 cifre significative.

Fonte: http://lnx.liceisgv.it/docenti/milani/files/2010/10/Misura-ed-errori.doc

Sito web da visitare: http://lnx.liceisgv.it/docenti/milani/

Autore del testo: non indicato nel documento di origine

Parola chiave google : Incertezza ed errori di misura tipo file : doc

Incertezza ed errori di misura