Fisica riassunti

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le onde

L’impulso è una perturbazione elementare che si propaga in un mezzo elastico. Un onda è composta da: la sorgente è la cosa che causa delle oscillazione, il mezzo di propagazione e il ricevitore. L’onda è un insieme di uno o più impulsi generati da forze esterne: essa si propaga nello spazio e nel tempo senza che ci sia alcuno spostamento della materia dalla sorgente al ricevitore, ma solo una traslazione rigida del profilo della perturbazione stessa. L’impulso può essere considerato un’informazione o un segnale di un cambiamento avvenuto a distanza. Matematicamente posiamo definire una funzione d’onda y = Ψ(x,t0) che fornisce al variare di x l’altezza dell’onda all’istante t fissato.
La funzione d’onda rappresenta in generale l’equazione del profilo dell’onda al variare della distanza x dalla sorgente e del tempo t trascorso. Le proprietà della funzione d’onda sono:

La funzione d’onda si ripete nel tempo ripresentandosi uguale a se stessa dopo un certo intervallo T; pertanto è una funzione periodica nel tempo di periodo T e di frequenza f =1/T. Ψ(x,t+T) = Ψ(x,t)
Essa è una funzione periodica anche nello spazio e ripropone il suo profilo a ogni distanza λ detta lunghezza d’onda. Ψ(x+λ,t) = Ψ(x,t)
L’ampiezza A dell’onda è uguale alla massima escursione verticale dalla situazione di quiete a x o a t fissato.
L’intero profilo dell’onda si sposta a velocità costante in direzione modulo e verso se non incontra ostacoli nel mezzo di propagazione in cui viaggia.

La funzione d’onda di un’onda armonica è y = Ψ(x - vt) = Acos[k(x – vt] = A cosα
k è una costante che ha le dimensioni fisiche del reciproco di una lughezza |L-1| poiché l’intero argomento α della funzione coseno deve essere espresso in radianti. La grandezza α = k(x – vt) è detta fase dell’onda. La velocità v presente nella fase dell’onda è detta velocità di fase v = λ/T
La funzione d’onda armonica è anche scritta come A cos (2πx/λ - 2πt/T).
Tutti i corpi a seconda della loro forma possono essere sottoposti a movimenti ondulatori di due tipi: onde trasversali, quando la direzione di propagazione del profilo dell’onda e il movimento della perturbazione dalla posizione di quiete sono perpendicolari; onde longitudinali quando hanno la stessa direzione. Nel caso di superfici o corpi estesi possiamo unire tutti i punti dell’onda aventi uguale spostamento dalla posizione di equilibrio (oppure uguale fase): il luogo geometrico cosi ottenuto è detto fronte d’onda.
I fronti d’onda delle onde trasversali possono essere: rettilinei (onde del mare) o circolari (sasso lanciato nell’acqua).
I fronti d’onda delle onde longitudinali possono essere: piani (spira di una molla) o sfere (onde sonore).

Le cariche elettriche, forze e campi

Ogni atomo di qualsiasi corpo umano contiene cariche positive e negative mantenute insieme da una forza attrattiva, simile alla gravità, ma enormemente più intensa. A loro volta gli atomi sono legati da forze elettriche per formare le molecole, e queste, infine, interagiscono fra loro per formare il corpo umano. In realtà, viviamo esprimendo continuamente qualche manifestazione dell’ elettricità.
Gli effetti della carica elettrica erano noti almeno fin dal 600 a.C. Esistono due tipi di carica: positiva (+) e negativa (-), proposti da Benjamin Franklin (1706-1790) nel 1747. Corpi che hanno una carica totale uguale a zero vengono detti «elettricamente neutri». Un esempio di oggetto elettricamente neutro è l’atomo. Gli atomi hanno un piccolo nucleo molto denso con carica positiva, circondato da una nuvola di elettroni carichi negativamente. Tutti gli elettroni hanno esattamente la stessa carica elettrica. Questa carica è molto piccola e ha, per definizione, l’intensità e data da: e = 1,60 . 10-19 C. In questa espressione C è un’unità di misura della carica chiamata coulomb, dal nome del fisico francese Charles-Augustin de Coulomb. Chiaramente, la carica di un elettrone, che è negativa, sarà –e. Al contrario, la carica di un protone è esattamente +e.
Un coulomb è una quantità significativa di carica; per esempio, anche un potente fulmine trasporta solo da 20 a 30 C. Una comune unità di misura della carica è il micro coulomb μC = 10-6 C.
Come mai strofinare un pezzo d’ambra con una pelliccia fornisce una carica all’ ambra? Inizialmente, si pensava che lo strofinio creasse la carica osservata. Ora invece sappiamo che strofinare la pelliccia sull’ ambra provoca un trasferimento di carica mantenendo invariata la quantità di carica totale. Prima di caricarsi, la pelliccia e l’ambra sono entrambe neutre. Durante lo strofinio, alcuni elettroni vengono trasferiti dalla prima alla seconda. In nessun istante, durante tale processo, è stata creata o distrutta qualche carica. Questo, infatti, è un esempio di una delle leggi fondamentali di conservazione della fisica:
La carica elettrica totale dell’Universo è costante. Nessun processo fisico può determinare un aumento o una diminuzione della quantità totale di carica dell’Universo.
In un solido, i nuclei degli atomi hanno posizioni fisse; gli elettroni esterni, invece, sono spesso poco legati e hanno posizioni fisse; gli elettroni esterni invece, sono spesso poco legati e abbastanza facilmente separabili dal nucleo. L’atomo che perde un elettrone diventa uno ione positivo, mentre chi lo riceve diventa uno ione negativo. Questo modo di caricare un oggetto è detto carica per separazione.
Poiché gli elettroni hanno sempre carica –e e i protoni hanno sempre carica +e, tutti i corpi devono avere una carica netta che è un multiplo intero di e. Descriviamo questa condizione dicendo che la carica elettrica è quantizzata.
La polarizzazione è quando gli atomi di un corpo neutro che viene avvicinato da un corpo carico positivamente o negativamente si dispongono in modo tale da avere la parziale carica opposta (negativa in caso di corpo carico positivamente o viceversa) rivolta verso la superficie. I materiali nei quali le cariche non sono libere di muoversi, sono chiamati isolanti. Molti di essi sono sostanze non metalliche e la maggior parte sono, anche, buoni isolanti termici. Molti metalli sono buoni conduttori di elettricità, j poiché permettono alle cariche di muoversi più o meno liberamente. A livello microscopico, la differenza tra conduttori e isolanti è che gli atomi di un conduttore permettono a uno o più degli elettroni più esterni di allontanarsi dal nucleo. Questi elettroni liberi, spesso chiamati ,«elettroni di conduzione», possono muoversi liberamente attraverso il conduttore. Gli isolanti, al contrario, hanno pochissimi elettroni liberi, o addirittura nessuno; gli elettroni sono legati ai propri atomi e non possono spostarsi all’interno del materiale. Alcuni materiali hanno proprietà intermedie fra quelle di un buon conduttore e quelle di un buon isolante. Questi materiali, chiamati semiconduttori, possono essere regolati in modo da mostrare quasi tutti i livelli di conducibilità desiderati, controllando la concentrazione dei componenti diversi di cui sono fatti. Un materiale fotoconduttore è il selenio, che conduce elettricità quando è illuminato ma è un isolante quando è al buio.
Abbiamo già visto che le cariche elettriche esercitano delle forze le une sulle altre. La 1egge che descrive queste forze fu formulata per la prima volta da Coulomb alla fine del Settecento. Supponiamo che una carica puntiforme ideale di intensità q1 si trovi a un a una distanza r da un’altra carica puntiforme di intensità q2. La legge di Coulomb dice che F = k · q1 · q2/r² con k = 8,99 . 109 N · m2/C2. Nella legge di Coulomb la direzione della forza è lungo la linea che congiunge i due cariche. Il verso dipende dalle cariche: se si attraggono o si respingono avremo versi diversi.
La legge di Coulomb è simile alla legge di Newton ella gravitazione universale F Gm1m2/r2. Ma si differenziano perché la legge di coulomb può essere sia attrattiva che repulsiva, mentre la seconda è solo attrattiva. Inoltre la prima è importante a livello atomico e microscopico, mentre la seconda a livello macroscopico. La forza di Coulomb è una grandezza vettoriale per questo nel caso di più di due forze occorre trovare la somma vettoriale delle forze per trovare quella totale. Questa proprietà è detta sovrapposizione delle forze. Nel caso di 3 forze lungo la stessa retta la direzione sarà la solita retta congiungente tra le 3 forze, mentre se si trovano sparse sul piano occorre scomporre i singoli vettori nelle loro componenti e eseguire la somma componente per componente.
Nel caso in cui al posto di una carica puntiforme avessimo una sfera con la carica uniformemente distribuita sulla sfera abbiamo lo stesso comportamento della carica puntiforme, ma introduciamo una nuova quantità, la densità di carica superficiale ovvero la quantità di carica per unità di superficie. Essa è definita con la lettera σ e si trova dividento la carica totale Q per l’area della sfera A: σ = Q/A.
Il campo elettrico è la zona che risente della carica elettrica ed è anche detto il rapporto tra forza e carica in una data posizione. Per esempio il campo elettrico E generato da una carica su una carica di prova q0 che risente di una forza F è regolato dalla seguente formula: E = F/q0 e la sua unità di misura è N/C. Il campo elettrico è un vettore che ha direzione radiale e verso uscente se la carica che lo genera è positiva e entrante se negativa.
Il campo elettrico generato da una carica puntiforme q su una carica q0 è E = k · q/r2. Questo deriva da E = F/q0 sostituendo alla F la legge di coulomb ovvero E = (k q q0/r2)/q0 che semplificato ritorna alla nostra formula.
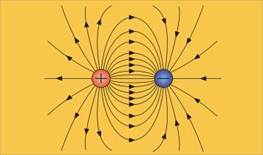Pe trovare il campo elettrico tra più cariche dobbiamo usare lo stesso metodo che abbiamo usato per la forza di Coulomb, ovvero quello della sovrapposizione.
Per disegnare le linee di forza del campo elettrico dobbiamo seguire 4 regole:

In ogni punto hanno la direzione del vettore campo elettrico E in quel punto
Partono dalle cariche positive o dall’infinito
Finiscono nelle cariche negative o all’infinito
Sono più dense dove E ha un’intensità maggiore; in particolare, il numero di linee entranti o uscenti da una carica è proporzionale all’intensità della carica.

Nel caso in cui la carica è disposta uniformemente su un piano abbiamo che il campo punta perpendicolarmente al piano e la sua intensità è indipendente dalla distanza dello stesso; inoltre nei punti lontani dal bordo del piano il campo elettrico è uniforme. Se poniamo due piani conduttori di questo tipo con carica opposta paralleli l’uno dall’altro a distanza d, otteniamo un condensatore a facce piane e parallele. In un tale sistema il campo tra le due facce è uniforme.
In un conduttore quando è raggiunto l’equilibrio le cariche si muovono verso l’esterno per allontanarsi dalle cariche dello stesso segno. Le cariche in eccesso su un conduttore, sia positive sia negative, si muovono verso la superficie esterna del conduttore.
Quando le cariche elettriche sono in equilibrio, il campo elettrico all’interno del conduttore è zero, E = 0. Con l’espressione all’interno del conduttore, vogliamo indicare un punto all’interno del materiale di cui esso è costituito, in contrapposizione a un punto che si trova in una cavità all’interno del conduttore stesso. Un conduttore scherma il suo interno dal campo elettrico. Le cariche negative si spostano verso la sorgente del campo elettrico e le cariche positive rimangono dall’altra parte. Le linee del campo elettrico esterno finiscono su8lle cariche negative e ripartono dall’altra parte e nel mezzo il campo è zero.
Le linee del campo elettrico cadono perpendicolarmente sulla superficie di un conduttore. Un corpo può essere caricato per contatto o per induzione. La carica per induzione avviene quando viene avvicinata una sbarretta carica negativamente ad una sfera scarica su base isolante. In questo caso nella parte della sfera più vicina alla sbarretta si avrà una maggiore concentrazione di carica positiva mentre dall’altra parte ci sarà più carica negativa. A questo punto la sfera è ancora neutra, ma se colleghiamo la sfera a terra le cariche negative passano alla Terra. Mantenendo la sbarretta vicino alla sfera e rimuovendo il filo avremo tolto cariche negative dalla sfera e quest’ultima è rimasta carica positivamente.
La carica per contatto avviene quando una sbarretta carica negativamente entra in contatto con una sfera metallica scarica su base isolante e qualche carica passa dalla sbarretta alla sfera nel punto di contatto.
Considerando un campo elettrico E che attraversa una superficie A perpendicolare al campo possiamo immaginare un flusso del campo elettrico attraverso la superficie. Il flusso Φ è pari al prodotto tra il campo e l’area Φ = E · A. Se la superficie è parallela alle linee del campo non c’è flusso.
Se il piano è inclinato le linee di E attraversano la superficie formando un angolo θ con la perpendicolare alla superficie e di conseguenza la componente di E perpendicolare alla superficie è E cosθ e la componente parallela al piano è E senθ. Però solo la componente perpendicolare genera flusso la formula è Φ = E · A · cos θ.
Se la superficie su cui è calcolato il flusso è chiusa il segno del flusso è:

Il flusso è positivo per le linee del campo elettrico che lasciano il volume chiuso della superficie
Il flusso è negativo per le linee del campo che entrano nel volume della superficie.

Prendendo ad esempio una carica puntiforme al centro di una superficie sferica possiamo arrivare alla legge del flusso elettrico: Φ = E · A = (kq/r2) · (4πr2) = 4πkq. Possiamo introdurre una nuova costante chiamata costante dielettrica del vuoto che è pari a 1/4πk e si identifica con ε0. Da ciò arriviamo a dire che Φ = 4πkq = q/ ε0. Questa legge detta Legge di Gauss è valida per qualunque carica q contenuta in una qualunque superficie arbitraria. Se la carica q è positiva le linee del campo lasciano il volume racchiuso dalla superficie e il flusso è positivo; se la carica è negativa le linee del campo entrano nel volume racchiudo dalla superficie e quindi il flusso è negativo.
Le superfici gaussiane non devono essere per forza sferiche. Consideriamo una lamina carica che ha campo perpendicolare ad essa e scegliamo per la nostra superficie gaussiana un cilindro posto perpendicolare alla lamina, Nessuna linea del campo attraversa la superficie laterale del cilindro e dobbiamo considerare solo le due basi di area A; perciò il nostro flusso è Φ = E(2A). Se la densità di carica è σ, la carica interna al cilindro è σA e arriviamo a dire che Φ = E(2A) = (σA)/ε0. Semplificando troviamo che E = σ/2ε0.
Osserviamo che E non dipende in alcun modo dalla distanza dalla lamina.
Se in campo non è uniforme su tutta la superficie occorre procedere nel seguente modo:

Suddividiamo la superficie in tanti parti ΔS (dove deltaS sta a significare una piccola parte di superficie) tali che in ognuna di esse il campo possa essere considerato uniforme
Calcoliamo, per ogni elemento di superficie ΔS il flusso: ΔΦ = E · ΔS
Sommiamo tutti i flussi per avere il flusso totale.

Se aumentiamo il numero di suddivisioni il calcolo si avvicina sempre di più alla precisione.

Potenziale elettrico ed energia potenziale elettrica

Le forze elettriche e quelle gravitazionali sono forze conservative, perciò esiste un’energia potenziale elettrica U. considerando un campo elettrico uniforme rivolto verso il basso, una carica di prova positiva q0, posta in questo campo, risente di una forza elettrica verso il basso. Se spostiamo la carica verso l’alto per un tratto d il lavoro della forza elettrica è: W = -q0Ed.
Ne deriva che la variazione dell’energia potenziale è: ΔU = -W = q0Ed. se la carica q0 è negativa si cambia tutto di segno. Il potenziale elettrico V è: ΔV = ΔU/q0 = -W/q0. Come per l’energia potenziale gravitazionale possiamo porre il potenziale elettrico uguale a 0 in qualsiasi posizione: e solo le variazioni di potenziale sono misurabile. L’unità di misura del potenziale è J/C che chiamiamo Volt (V). l’energia in Joule può essere espressa come il prodotto della carica in C e del voltaggio. L’unità di misura dell’energia in questo caso è l’elettronvolt (eV) che è il prodotto della carica dell’elettrone per la differenza di potenziale di 1 V. 1 eV = 1,60 · 10-19 J
Da ciò ricaviamo che il potenziale elettrico è E · d0. Da ciò diciamo che E = ΔV/d.
Questa relazione ci mostra che il campo elettrico può essere espresso in N/C o in V/m. il campo elettrico dipende dalla rapidità di variazione del potenziale elettrico rispetto allo spostamento. Il potenziale elettrico diminuisce se ci muoviamo nella direzione del campo elettrico.
Considerando una carica puntiforme positiva q fissata nell’origine di un sistema di coordinate e una carica di prova positiva q0 ferma in un punto A. la carica di prova risente di una forza repulsiva e se la lasciamo libera si allontanerà. Quando raggiungerà un punto ipotetico B la sua energia cinetica sarà aumentata della stessa quantità di cui è diminuita la sua energia potenziale, perciò l’energia potenziale è maggiore nel punto A rispetto al punto B.
Se scegliamo di porre uguale a 0 il potenziale elettrico in una posizione infinitamente lontana dalla carica data possiamo arrivare a dire che il potenziale elettrico ha una distanza r è: V = kq/r dove k è la costante di della forza di coulomb e q è la carica positiva puntiforme prima citata. Si ricorda che V è sempre una variazione di potenziale, però in questo caso abbiamo posto V ad una distanza infinita uguale a 0 e quindi rimane solo V e non ΔV.
L’energia potenziale è: U = q0V = kq0q/r. l’energia potenziale di due cariche separate da una distanza infinita è 0.
Il potenziale elettrico di una carica puntiforme vicino ad una carica positiva tende a più infinito se ci avviciniamo ad essa e a 0 se ci allontaniamo, formando un picco di potenziale. Il potenziale elettrico di una carica puntiforme vicino ad una carica negativa tende a meno infinito avvicinandosi ad essa e a 0 se ci allontaniamo, formando una buca di potenziale.
Se la carica nell’ origine è positiva una carica di prova positiva si allontanerà dall’ origine. Se è negativa la carica di prova scivolerà nella buca di potenziale. Il potenziale elettrico totale dovuto a due o più cariche è uguale alla somma dei potenziali delle singole cariche e vale il principio di sovrapposizione.

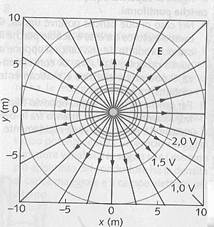
Considerando una singola carica positiva nell’ origine le linee di livello mostrate su un grafico bidimensionale indicano il valore di potenziale. Poiché il valore di potenziale in ogni punto di una data linea è uguale a quello di qualsiasi altro punto sulla stessa curva esse sono dette superfici equipotenziali. Queste superfici ci danno informazioni sul campo elettrico; esso è più intenso nei pressi della carica dove le superfici equipotenziali sono più vicine fra loro rispetto a quando è più lontano dalla carica. Perciò possiamo dire che il campo elettrico punta nella direzione in cui diminuisce il potenziale elettrico ed esso è sempre perpendicolare alle superfici equipotenziali e il potenziale è
costante nella direzione perpendicolare al campo elettrico.

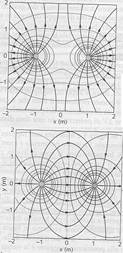
Nel caso di due cariche positive di uguale intensità la
regione in mezzo alle due cariche ha potenziale costante
e campo elettrico nullo. Se le due cariche sono di segno
opposto esse formano un dipolo elettrico, il fra le cariche e
il potenziale è zero.

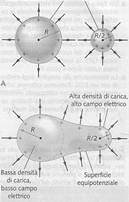I conduttori ideali sono superfici equipotenziali, tutti i punti su questi conduttori oppure al loro interno sono allo stesso potenziale. Se il conduttore ha la forma di una sfera, la carica si distribuisce uniformemente sulla sua superficie. Se ha forma più appuntita da una parte e più piana da un'altra la carica è più concentrata vicino alla punta dove il campo è più intenso. Per capire ciò consideriamo una sfera di raggio R con una carica Q distribuita sulla sua superficie. Sappiamo che la densità di carica è σ = Q/4πR² e quindi il potenziale elettrico è V = 4πkσR. Se il raggio della sfera è la metà la densità di carica sarà doppia e quindi otteniamo lo stesso potenziale di prima.
Invece il campo elettrico è maggiore per la sfera più piccola: nella sfera grande è 4πkσ, mentre nella sfera piccola abbiamo una densità di carica doppia e quindi doppio campo elettrico. Per cui in un conduttore di forma qualsiasi la parte del conduttore con maggiore curvatura ha una maggiore densità di carica e campo elettrico più intenso. Inoltre il campo elettrico incontra la superficie del conduttore formando un angolo retto.
Il condensatore deve il suo nome alla sua capacità di immagazzinare cariche elettriche ed energia. Esso è costituito da due conduttori dette armature che se vengono collegate ai poli di una batteria si caricano e una acquista carica Q e l’altra –Q. se la batteria produce una differenza di potenziale di V volt fra i suoi poli si accumula una carica Q e il loro rapporto da c ovvero la capacità del condensatore. C = Q/V.
Q e V sono sempre in valore assoluto e C è sempre positivo. La capacità si misura in Farad F. 1 farad = 1 coulomb/1 volt.
Un condensatore molto semplice è quello a facce piane parallele con armature di area A poste a distanza d. Il suo campo elettrico è E = σ/ε0 oppure E = Q/Aε0. LA sua differenza di potenziale è ΔV = -EΔS =(Q/ε0A)d. La sua capacità è C = Q/V = Q/(Q/ε0A)d = ε0A/d.
La capacità è direttamente proporzionale all’area e inversamente proporzionale alla differenza di potenziale e alla distanza.
Per aumentare la capacità di un condensatore inseriamo fra le armature un materiale isolante detto dielettrico. Le sue molecole si allineeranno col campo del condensatore ovvero con la carica positiva sulla superficie del dielettrico vicina all’armatura negativa e la carica negativa vicina all’armatura positiva. Nel dielettrico c’è un campo ridotto che segue la formula E = E0/εr (dove E è il campo del dielettrico, E0 è il campo del condensatore e εr è la costante dielettrica relativa che nel vuoto è 1 e nei materiali isolanti è maggiore di 1). Il dielettrico fa variare anche la differenza di potenziale e la capacità:
V (differenza di potenziale del dielettrico) = Ed = (E0/εr)d = V0/εr (dove V0 è la differenza di potenziale del condensatore.
C (Capacità del dielettrico) = Q/V = Q/V0/εr = εr · C0 (dove C0 è la capacità del condensatore).
Il dielettrico scherma parzialemente le armature rendendo più facile accomulare cariche su di esse. Nel caso di un condensatore a facce piane parallele riempito da un dielettrico C = εrε0A/d.
Se il campo elettrico applicato ad un dielettrico è abbastanza elevato, può rompere gli atomi, permettendo al dielettrico di condurre elettricità, provocando la rottura del dielettrico. Il campo massimo che un dielettrico può sopportare prima di rompersi è detto rigidità del dielettrico.

Corrente elettrica e circuiti

Un flusso di cariche elettriche da un punto ad un altro è chiamato corrente elettrica. La carica è trasportata da elettroni. Una carica ΔQ che attraversa una certa sezione di filo in un tempo Δt ha intensità di corrente elettrica      I = ΔQ/Δt. L’ unità di misura è l’ampere A che è 1 coulomb fratto 1 secondo.
Chiamiamo circuito elettrico il percorso chiuso compiuto da una carica per tornare nel suo punto di partenza. I circuiti di corrente continua detti CC nei quali la corrente scorre sempre nella stessa direzione. I circuiti in cui la corrente inverte periodicamente la sua direzione sono detti circuiti in corrente alternata.
Una batteria utilizza delle reazioni chimiche per produrre una differenza di potenziale ai sistemi detti anche poli o terminali. Il terminale corrispondente al terminale elettrico più alto è indicato con il segno +, quello corrispondente al potenziale elettrico più basso è indicato con il segno -. La differenza di potenziale elettrico fra i terminali della batteria quando questa è staccata dal circuito è detta forza elettromotrice o fem, ε. Però questa non è una forza ma la quantità di lavoro effettuata da una batteria per muovere una determinata quantità di carica lungo un circuito.            W = ΔQ∙ε.
Il verso della corrente in un circuito è il verso in cui si muoverebbe una carica di prova positiva. In realtà a muoversi sono gli elettroni negativi. I fili reali dove si muovono gli elettroni provocano una resistenza. Per far si che gli elettroni si muovano contro la resistenza del filo è necessario applicare ai suoi estremi una differenza di potenziale. V = I∙R da cui ricaviamo R = V/I dove secondo la legge di Ohm R è la resistenza, V la differenza di potenziale e I l’ intensità. L’ unità di misura della resistenza è Ω un ohm che è uguale a 1 volt fratto 1 ampere.
In un circuito elettrico una resistenza è segnalata da una linea a zigzag; le linee dritte indicano fili reali con resistenza zero; per indicare la resistenza di un filo reale includiamo semplicemente un resistenza del valore appropriato.
Supponiamo di avere un pezzo di filo di lunghezza L e con una sezione di area A. la R di questo filo dipende dal materiale di cui è fatto. La grandezza che caratterizza la resistenza do un dato materiale è la sua resistività o resistenza specifica ρ. R = ρ(L/A).
Un filo nel quale scorre una corrente elettrica può diventare molto caldo: perché gli elettroni urtano gli atomi del filo e quest’ ultimi vibrano con una maggiore energia cinetica che fa aumentare la resistenza. Alcuni materiali detti semiconduttori all’ aumentare della temperatura mostrano una diminuzione della resistività. Alcuni materiali a temperature bassissime, vicine allo 0 assoluto, vedono la proprio resistenza diventare 0 e quindi sono detti super conduttori.
Una carica ΔQ si muove attraverso una differenza di potenziale V la sua energia potenziale elettrica U varia: ΔU = ΔQ∙V.
La potenza è uguale a: P = ΔQ∙V/Δt da cui ricaviamo P = I∙V. Nel caso di una resistenza la potenza elettrica è dissipata sottoforma di calore. Possiamo scrivere la potenza dissipata in una resistenza come P = I²R oppure V²/R.
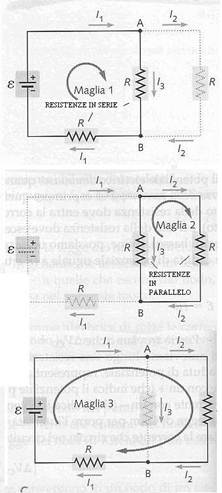
Per ciascun tipo di circuito con più resistenze possiamo trovare la resistenza equivalente. Se le resistenze sono collegate una dopo l’ altra e sono quindi in serie possiamo dire che attraverso ciascuna resistenza deve passare la stessa corrente I, di conseguenza le differenze di potenziale di 3 resistenze in serie sono: V1 = I∙R1    V2 = I∙R2         V3 = I∙R3. Sappiamo che la fem ε è la somma delle 3 differenze di potenziale ε = V1+V2+V3. Quindi ε = I∙R1 + I∙R2 + I∙R3, raccogliendo I viene ε = I(R1+R2+R3). La somma delle resistenze in serie è la resistenza equivalente             ε = I∙Req.
Le resistenze sono in parallelo quando sono collegare alla stessa differenza di potenziale in un caso come questo la corrente dispone di percorsi paralleli attraverso i quali può passare la corrente totale I che si divide nelle 3 strade percorribili     I = I1+I2+I3     poiché la differenza di potenziale è la stessa per ciascuna resistenza la corrente che passa al loro interno è:    I1 = ε/R1   I2 = ε/R2   I3 = ε/R3 che sommate diventano I = ε/R1+ ε/R2+ ε/R3 = ε(1/R1+1/R2+1/R3).
Per ricavare la resistenza equivalente facciamo: 1/Req =1/R1+1/R2+1/R3. Da questo troviamo l’equazione finale       I = ε(1/Req). Perciò più resistenze colleghiamo in parallelo minore è la resistenza equivalente. Se in un collegamento una delle resistenze è uguale a zero anche la resistenza equivalente è uguale a 0. Questa situazione è detta cortocircuito, in questo caso tutta la corrente passa attraverso il cammino con resistenza nulla.
Se ci sono resistenze in serie e in parallelo prima si calcola la resistenza equivalente di quelle in parallelo che diventa un’altra resistenza in serie e infine si calcola la resistenza equivalente.
La legge dei nodi di Kirchhoff deriva dall’osservazione che la corrente che entra in un qualsiasi punto di un circuito deve essere uguale alla corrente che esce da quel punto. Un nodo è un punto del circuito dover si incontrano 3 più fili. Se associamo un segno + alle correnti ch entrano nel nodo e un segno – a quelle che escono dal nodo la somma algebrica di tutte le correnti che c0onvergono in un nodo deve essere uguale a zero.

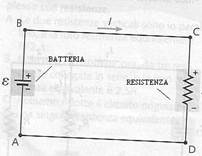Un qualsiasi circuito chiuso è chiamato maglia il potenziale elettrico aumenta di una quantità uguale a ε nell’andare al punto A al punto B poiché ci muoviamo dal terminale della batteria a basso potenziale verso quello ad alto potenziale. Da B a C non c’è nessuna variazione di potenziale. Da C a D il potenziale varia perche si attraversa una resistenza. Questa variazione è detta ΔVcd. Tra D e A non c’è alcuna differenza di potenziale, il potenziale elettrico diminuisce quando ci muoviamo lungo una resistenza. Secondo la legge delle maglie di Kirchhoff la somma algebrica di tutte le differenze di potenziale lungo una maglia chiusa in un circuito è zero ε+ΔVcd=0.

In un circuito dove sono presenti condensatori posti in parallelo ogni condensatore ha la stessa differenza di potenziale ε fra le armature. Se sono 3 avremo le seguenti formule:
Q1 = C1∙ε Q2 = C2∙ε Q3 = C3∙ε dove Q è la carica e C la capacità per cui la carica totale sui tre condensatori è Q = Q1 + Q2 + Q3 = ε∙C1 + ε∙C2 + ε∙C3 = ε(C1 + C2 + C3).
Da ciò ricaviamo la capacità equivalente Ceq = C1 + C2 + C3 quindi Q = Ceq∙ε.

I condensatori in parallelo si combinano come le resistenze in serie, mentre i condensatori in serie come le resistenze in parallelo. La batteria fa si che l’armatura di sinistra di C1 acquisti una carica positiva Q+, che attrae una carica negativa Q- sull’armatura di destra. Quest’ultima fa caricare l’armatura sinistra di C2 con una carica positiva perché tra i due condensatori c’è carica 0. La carica negativa attrae una carica negativa Q- sull’armatura di destra di C2 che fa caricare l’armatura sinistra di C3 con una carica positiva che attrae una carica negativa Q- sull’armatura di destra di C3. I tre condensatori in serie hanno una carica della stessa entità sulle loro armature.
La differenza di potenziale di ciascuno di essi è: V1 = Q/C1 V2 = Q/C2 V3 = Q/C3 da cui ε = V1 + V2 + V3 = Q/C1+ Q/C2+ Q/C3 = Q(1/C1 + 1/C2 + 1/C3) per cui la capacita equivalente è 1/Ceq = 1/C1 + 1/C2 + 1/C3 da cui ε = Q(1/Ceq)
In questo caso è come se la distanza fra le armature dei singoli condensatori aumentasse e diminuisse la capacità.

Il campo magnetico

Gilbert fu il primo a studiare i fenomeni magnetici. Egli individuò nella Terra il grande magnete causa dell’orientamento degli aghi magnetici usati nelle bussole. Un ago magnetico si orienta con una estremità verso il polo nord terrestre e con l’altra verso il polo sud. Le due estremità dell’ago sono per questo dette polo nord e sud. Se nelle vicinanze dell’ago sono presenti dei magneti, l’ago risente dell’attrazione magnetica di questi corpi: il suo polo nord viene attratto da quello del magnete e respinto dal polo sud del magnete. L’opposto accade al polo sud dell’ago. Una normale sbarretta di acciaio non è in grado di attrarre piccoli oggetti di ferro, ma se l’avviciniamo o mettiamo in contatto con della magnetite essa acquisisce la proprietà di attrarre gli oggetti in ferro: si dice che la sbarretta è magnetizzata. Gli aggetti che acquistano artificialmente le proprietà magnetiche sono detti calamite o magneti artificiali. Gilbert studiò inoltre le analogie tra le cariche elettriche e i poli magnetici.
La prima differenza è che non è possibile separare i poli magnetici di una calamita, infatti se si taglia a meta una calamita si formano due calamite che hanno entrambi i poli. Per questo aghi e calamite sono detti anche dipoli elettrici
La seconda è che mentre un corpo elettrizzato attira piccoli corpi di differenti sostanze la calamita attira pezzetti di ferro o altri metalli. Infine analogamente alle cariche elettriche poli magnetici diversi si attraggono mentre poli uguali si respingono.
Coulomb fu il primo a capire che l’intensità delle forze magnetiche diminuisce con il quadrato della distanza tra i poli. Il campo magnetico vettoriale B ha per direzione la retta lungo la quale si dispone un ago magnetico posto in un punto e verso quello che va dal polo sud al polo nord. Possiamo costruire con un ago magnetico le linee del campo magnetico, la direzione del vettore campo magnetico è la direzione della tangente alla linea del campo.
Oersted dimostrò che un filo percorso da corrente elettrica provoca la deviazione di un ago magnetico posto nelle sue vicinanze ovvero il passaggio di corrente in un filo genera campo magnetico. Se mettiamo un filo conduttore lungo la direzione del campo magnetico terrestre e sotto un ago magnetico parallelamente al filo quando facciamo passare la corrente l’ago oscilla e si dispone perpendicolarmente al filo. Se invertiamo il verso della corrente l’ago si mette sempre perpendicolare al filo ma orientato in modo opposto. Le linee del campo magnetico generato dal filo percorso dalla corrente sono le infinite circonferenze concentriche di cui il filo costituisce l’asse. Il verso si ottiene con la regola della mano destra ovvero indicando col pollice il verso della corrente, le dita della mano chiudendosi indicano il verso delle linee del campo. Con questa esperienza capiamo che la corrente genera un campo magnetico e che la forza non è diretta lungo la congiungente i due corpi, ma perpendicolare al piano che contiene il filo e l’ago.
Faraday scopri che un magnete esercita una forza su un conduttore percorso da corrente: egli ha disposto in un campo magnetico un filo conduttore sospeso in modo da potersi muovere lungo la direzione verticale. Quando si fa passare corrente il filo subisce una forza perpendicolare al campo che è lungo la direzione orizzontale e quindi il filo si muove verso il basso.
Ampere invece ha dimostrato che due fili conduttori rettilinei e paralleli si attraggono se la corrente li percorre nello stesso verso e si respingono se la corrente li percorre in versi opposti. La forza che si esercita ha modulo F = k l i1 i2 / r dove l è la lunghezza del filo sul tratto su cui si esercita la forza, i1 e i2 sono le intensità di corrente, r è la distanza dei fili e k è una costante che è pari a k = μ0/2π e μ0 è una costante detta permeabilità magnetica del vuoto. La costante k vale numericamente 2 ∙ 10-7 e la sua unità di misura è N/A².

Il campo magnetico

Disponiamo nello spazio vuoto un filo rettilineo molto lungo attraversato da corrente di intensità i diretta verso l’alto. Sappiamo che esso genera un campo magnetico con linee di forza circolari con verso antiorario. Se poniamo a distanza r dal filo una carica elettrica positiva q, in moto con velocità v e misuriamo la forza F a cui è sottoposta verifichiamo che: F è perpendicolare al piano contenente v e campo elettrico B; il modulo della forza è uguale a F = k q i v senα/r, dove k è una costante, α l’angolo tra i vettori v e B. v senα è la componente della velocità perpendicolare al campo magnetico quindi se alfa è uguale a 0 la forza è nulla, se α è 90° la forza è massima. La sua direzione è perpendicolare al piano su cui si trovano B e v.
Il verso della forza si ottiene con la regola della mano destra: se il pollice rappresenta il vettore v e l’indice il vettore B il medio aperto perpendicolarmente alle altre due dita indica il verso di F.
Se utilizziamo la definizione di prodotto vettoriale e indichiamo con u un versore ovvero un vettore unitario che ha la stessa direzione e verso di B l’equazione può essere riscritta come F = k q i v X u / r oppure q v X k i u / r. Da ciò possiamo ricavare l’espressione del vettore B campo magnetico che dipende dalle grandezza caratteristiche della sorgente del campo, dalla posizione in cui lo si misura e da una costante. Per cui il modulo di B è B = k i / r e il vettore è B = k i u / r.
Possiamo quindi riscrivere la forza che viene detta di Lorentz che è il fisico che per primo la determinò: F = qv X B.
O in modulo F = q v B senα. L’unità di misura del campo magnetico è T tesla ed è N/A m.
Se nella regione dello spazio in cui si trova la carica è presente anche un campo elettrico E la forza agente sulla carica è: F = q E + q v X B = q(E + v X B) che è l’espressione generale della forza di Lorentz.
La forza che agisce su un filo percorso da corrente elettrica immerso in un campo magnetico è F = i l X B, dove i è l’intensità di corrente, l è un vettore avente come modulo la lunghezza del conduttore e B è il vettore campo magnetico. In modulo essa è F = i l B senα. L’analogia con la formula di Lorentz non è casuale perché la corrente può essere pensata come una successione di cariche in moto con la stessa velocità costante.
Infatti sapendo che l’intensità di corrente può essere rappresentata come il prodotto tra il numero delle cariche per unità di volume n perla carica di una singola particella e per l’are della sezione del conduttore S e vd il vettore che rappresenta la velocità di deriva delle cariche (quindi i = n e S vd) possiamo scrivere F = n e S l vd X B che è uguale a scrivere F = i l X B dove il vettore l ha modulo uguale alla lunghezza del conduttore, direzione coincidente con quella del conduttore e verso come quello della corrente.
Anche da quest’ultima equazione possiamo ricavare B che è B = F / i l.
Considerando due fili paralleli percorsi da correnti di uguale verso e diciamo che la forza esercitata dal campo magnetico del primo filo B1 sul filo 2 è F2 = i2 l2 X B1 dove i2 è la corrente che passa per il secondo filo e l2 la sua grandezza. Il modulo di F2 = i2 l2 b1 senα, ma siccome α è 90° possiamo scrivere solo F2 = i2 l2 B1.
Sapendo che B1 è B1 = k i1/r si arriva a dire che F2 = k i1 i2 l2 /r .
La direzione di F2 è perpendicolare al piano individuato dalla direzione del filo 2 e del campo magnetico B. Il verso si ricava con la regola della mano destra.
Da ciò arriviamo alla formula di B = μ0 i / 2πr che è la legge di Biot e Savart ed esprime il vettore campo magnetico generato da una corrente di intensità i che scorre in un filo rettilineo.

Il campo magnetico

Considerando due fili paralleli percorsi da correnti di uguale verso e diciamo che la forza esercitata dal campo magnetico del primo filo B1 sul filo 2 è F2 = i2 l2 X B1 dove i2 è la corrente che passa per il secondo filo e l2 la sua grandezza. Il modulo di F2 = i2 l2 b1 senα, ma siccome α è 90° possiamo scrivere solo F2 = i2 l2 B1.
Sapendo che B1 è B1 = k i1/r si arriva a dire che F2 = k i1 i2 l2 /r .
La direzione di F2 è perpendicolare al piano individuato dalla direzione del filo 2 e del campo magnetico B. Il verso si ricava con la regola della mano destra.
Da ciò arriviamo alla formula di B = μ0 i / 2πr che è la legge di Biot e Savart ed esprime il vettore campo magnetico generato da una corrente di intensità i che scorre in un filo rettilineo.
Se consideriamo la forza sul filo 1 sarà F1 = μ0 i1 i2 l1/ 2πr.
Tramite il principio della sovrapposizione possiamo arrivare a trovare il campo generato da una spira e da un solenoide.
Con il termine spira si intende un filo conduttore chiuso di forma circolare. Immaginando di suddividere la spira in tratti di lunghezza infinitesima tali che possano essere considerati segmenti rettilinei possiamo determinare il campo da essa generato. Sommando i contributi di tutti i tratti si ottiene il vettore campo magnetico della spira. Il verso si ottiene con la regola della mano destra: se il pollice indica il verso della corrente nella spira le dita della mano chiudendosi indicano il verso delle linee di forza. Supponendo che la spira sia una circonferenza di raggio R il campo magnetico al centro è B = μ0 i / 2 R. La direzione sarà perpendicolare al piano che contiene la spira e il verso si ottiene sempre con la regola della mano destra con le dita della mano chiusa che indicano il verso della corrente e il pollice che indica il verso di B.
Un solenoide è un avvolgimento costituito da un filo conduttore avvolto a elica. Esso equivale ad un sistema di spire circolari tutte uguali affiancate. Nel caso la lunghezza del solenoide sia molto maggiore del suo raggio il campo magnetico è uniforme al suo interno e praticamente nullo all’esterno. All’interno del solenoide la direzione delle linee di forza del campo è parallela al suo asse e il verso è dato dalla regola della mano destra con le dita della mano chiusa che indicano il verso della corrente che circola nel solenoide e il pollice che indica il verso di B. Il campo magnetico all’interno di un solenoide può essere considerato come somma vettoriale dei campi magnetici generati da ogni singola spira. L’intensità del campo è B = μ0 N i / l. Dove N è il numero delle spire i la corrente che lo attraversa e l la sua lunghezza. Indicando con n = N/l il numero delle spire per unità di lunghezza possiamo scrivere anche B = μ0 n i.
Possiamo anche studiare la forza che agisce su una spira di forma rettangolare. La forma rettangolare è solo legata alla semplicità della trattazione: le conclusioni valgono per tutti i circuiti chiusi. Se consideriamo il campo magnetico prodotto dalla corrente che scorre nella spira in un punto sufficientemente lontano dalla spira stessa allora il campo è assimilabile a quello di un magnete a forma di barra, ossia ad un dipolo magnetico. Una spira posta in un campo magnetico parallelo ad essa a causa del verso della corrente nei suoi differenti rami è soggetta ad una coppia di forze che tende a farla ruotare. Perché nei tratti orizzontali della spira non agiscono forze essendo paralleli al campo. La spira ruota fino a disporsi in modo perpendicolare al campo. In questa posizione le forze tendono a deformare la spira e non più a muoverla. In questa situazione il momento di tutte le forze è nullo. Essa è sottoposta a un momento meccanico M di modulo M = F l sen α = i l B l sen α = i l² B sen α = i S B sen α.
Dove S è la superficie della spira e α l’angolo tra la direzione della forza e il piano che contiene la spira.
Introduciamo il vettore m che chiameremo momento magnetico della spira o momento di dipolo con le seguenti caratteristiche:

Modulo uguale a i S
Direzione perpendicolare al piano della spira
Verso definito dalla regola della mando destra: se le dita della mano chiudendosi indicano il verso della corrente che circola nella spira, il pollice indica il verso del vettore momento magnetico

Se indichiamo con n un versore perpendicolare al piano della spira, con verso definito dalla regola della mano destra, possiamo scrivere il momento magnetico della spira come: m = i S n
L’unità di misura del momento magnetico è A m² (ampere per metro quadrato). Il momento meccanico M che agisce sulla spira si può scrivere allora come: M = i S n X B = m X B. Con modulo M = m B sen α. Dove α è l’angolo formato tra i vettori m e B.

Il campo magnetico

Il flusso del campo magnetico B attraverso una superficie S è uguale al prodotto scalare tra il vettore B e il versore n perpendicolare alla superficie, moltiplicato per il valore della superficie S. Φ = B ∙ n S = B S cosα
In generale dove la superficie non è piana o il campo non è uniforme in tutti i punti della superficie è necessario suddividere la superficie in parti molto piccole da considerarle piane e sommare i flussi.
Il flusso generato da un filo percorso da corrente su una superficie cilindrica è nullo; infatti la direzione del campo è parallela alle basi e il campo non le attraversa, ma non attraversa neanche la superficie laterale perché è diretto lungo la tangente. Se consideriamo uno spicchio di cilindro dove non passa il filo conduttore possiamo dire che il flusso è nullo sulle superfici superiore, inferiore, frontale, posteriore. Sulla superficie destra e sinistra avremo Φ = BS e Φ = -BS. Perché esse sono disposte lungo i raggi del cilindro e sono perpendicolari alla direzione del campo, però il verso delle superfici è opposto quindi i due flussi sono uguali, ma di segno opposto; sommando tutte le componenti torniamo sempre a 0 quindi possiamo concludere che il flusso del campo magnetico attraverso una qualsiasi superficie chiusa è 0. Questo è il teorema di Gauss. Questo ci fa capire che a differenza del campo elettrico le linee del campo sono aperte, mentre le linee del campo magnetico sono chiuse, perché nel campo magnetico non è possibile separare i poli, mentre nel campo elettrico possiamo separare le cariche.
La circuitazione del campo B lungo una linea chiusa è Cb = ∑ B ∙ ∆s dove si intende che la linea generica chiusa sia stata suddivisa in intervalli piccolissimi ∆s in cui il campo B possa esse considerato costante. La circuitazione è quindi la somma dei prodotti scalari tra B e ∆s.
Consideriamo il campo generato da un filo percorso da corrente. Le linee di forza del campo sono circonferenze concentriche con il filo; il modulo del campo è B = ki/r e come ∆s possiamo indicare la circonferenza 2πr quindi Cb = ∑ B ∙ ∆s = ki2πr/r = μ0 i2πr/2πr = μ0 i. Da qui è evidente che la circuitazione non dipende dal raggio della circonferenza.
Consideriamo ora la circuitazione lungo una linea ABCDA che non circonda il filo. La circuitazione risulta nulla nei tratti AB e CD perché in questi tratti il campo è perpendicolare allo spostamento. Nei tratti BC e DA siccome la circuitazione non dipenda dal raggio è uguale nei due tratti, ma il segno è opposto perché i due tratti vengono percorsi in senso opposto: i loro contribuiti alla circuitazione si annullano e la circuitazione totale lungo i due tratti è uguale a 0. Possiamo concludere dicendo che la circuitazione lungo una linea chiusa che non circonda il filo è uguale a 0.
Se prendiamo diversi fili percorsi da corrente la circuitazione lungo una linea chiusa che li circonda è la somma delle circuitazioni dei campi generati dalle singole correnti, ma occorre associare un segno algebrico ad ogni circuitazione: positivo se il campo generato ha lo stesso verso di percorrenza della linea chiusa, negativo nel caso opposto. La circuitazione risulta Cb = μ0 (i1 + i2 + i3).
Per determinare quanto detto si introduce in concetto di corrente concatenata. Una corrente si dice concatenata a una linea chiusa se attraversa la superficie delimitata dalla linea chiusa. Arriviamo cosi ad enunciare il teorema di Ampere: la circuitazione di un campo magnetico B lungo una linea chiusa è uguale alla somma algebrica delle correnti concatenate alla linea stessa Cb = μ0 ∑ i. Il teorema di Ampere mette in relazione cosi come il teorema di Gauss per il campo elettrico, il campo con le sue sorgenti: il campo elettrico e le cariche, il campo magnetico e le correnti: poiché il campo magnetico ha una circuitazione lungo una linea chiusa diversa da 0 esso non è conservativo e non è possibile parlare di energia potenziale magnetica. Una forza si dice conservativa quando la sua circuitazione lungo una linea chiusa è 0.

Circuitazione e campi gravitazionali e elettrici

Sia il campo elettrico che il campo gravitazionale hanno un carattere radiale, ovvero le interazioni presentano le seguenti caratteristiche:

Sono dirette lungo la congiungente dei corpi che interagiscono
La loro intensità dipende solamente dalla distanza dei corpi, o in altri termini i due campi sono conservativi.

La forza gravitazionale newtoniana è conservativa perché il lavoro compiuto lungo una qualunque linea chiusa è nullo. Quindi il lavoro per spostare un corpo di massa m da un punto A a un punto B non dipende dal percorso seguito, ma solamente dalla posizione dei due punti. ∑ F ∙ ∆s = 0 per ogni linea chiusa.
La circuitazione del campo gravitazionale H lungo L è ∑ H ∙ ∆s dove ∆s rappresenta uno spostamento elementare lungo la linea chiusa L su cui il campo può essere considerato costante. Quindi possiamo affermare che: un campo H è conservativo se la sua circuitazione lungo una linea chiusa è nulla ∑ H ∙ ∆s = 0 per ogni linea chiusa.
La circuitazione di un campo cosi come il flusso non è una grandezza fisica ma una matematica. Il campo gravitazionale è conservativo perché è conservativa la forza gravitazionale. Quindi la funzione energia potenziale sarà U = - G M m / R e il potenziale gravitazionale V = U / m = - G M / r.
Per quanto riguarda il campo elettrico sappiamo che se esso è generato da una carica puntiforme è conservativo e in base al principio di sovrapposizioni tutti i campi elettrici formati da cariche in quiete sono conservativi.
La circuitazione del campo elettrico E lungo una linea chiusa è nulla ∑ E ∙ ∆s = 0 per ogni linea chiusa.
La funzione energia potenziale elettrica esprime il lavoro della forza elettrica per spostare una carica q da un punto A a un punto B distanti rispettivamente Ra e Rb da una carica Q sorgente del campo.
L = U(A) – U(B) = Q q/4 π ε0 (1/Ra – 1/Rb)
Se poniamo uguale a 0 l’energia potenziale di una carica posta a distanza infinita dalla carica sorgente Q U(B) = 0 abbiamo U(A) = Q q/4 π ε0 Ra

Moto di cariche in campi elettrici e magnetici

Sappiamo che su una particella carica q in moto o in quiete in un campo elettrico E agisce una forza di intensità F = qE. E’ possibile calcolare quindi l’accelerazione cui è sottoposta. L’accelerazione elettrica che agisce sulla carica q è: a = qE/m
Un caso abbastanza semplice da studiare è quello di un campo elettrico uniforme, cioè costante in intensità, direzione e verso, per esempio quello che esiste tra le piastre di un condensatore piano. L’accelerazione che agisce sulla carica q è a = qE/m cioè un accelerazione e cosante in modulo, diretta secondo la direzione del campo e con verso uguale a quello del campo oppure opposto a seconda che la carica sia positiva o negativa. Il moto è uniformemente accelerato.
Nel caso di campi conservativi possiamo pensare che l’energia potenziale elettrica di una particella carica in un campo elettrico si possa trasformare in energia cinetica e viceversa. Utilizzano la legge di conservazione dell’energia possiamo cosi calcolare per esempio la velocità raggiunta da un elettrone accelerato da un campo elettrico uguagliando la variazione dell’energia potenziale elettrica con la variazione della sua energia cinetica. U = Ec che diventa qΔV = ½mv².
Sappiamo che su una particella carica in moto in un campo magnetico agisce la forza di Lorentz. Dal momento che la forza di Lorentz è perpendicolare al vettore velocità essa compie sempre lavoro nullo. L = FΔs cosα, ma se l’angolo è 90 il coseno è zero perciò L = ΔEc = 0. Anche la variazione di energia cinetica è zero. La velocità della parritcella carica in moto all’interno del campo magnetico resta dunque costante in modulo. Inoltre se la direzione del campo è la velocità della carica sono perpendicolari, la carica si muove di moto circolare uniforme, perché sottoposta solo alla forza di Lorentz, che è una forza centripeta sempre perpendicolare alla velocità; la forza centripeta è data da F = mv²/r, dove m è la massa della particella ed r il raggio della traiettoria circolare. Eguagliando l’equazione della forza di Lorentz e quest’ultima abbiamo mv²/r = qvB da cui si ricava il raggio della traiettoria circolare r = mv/qB.
Il raggio della traiettoria circolare della particella carica all’interno del campo magnetico è direttamente proporzionale alla quantità di moto della particella e inversamente proporzionale all’intensità del campo magnetico e alla carica della particella. Il periodo del moto circolare è: T = 2πr/v = 2πmv/vqB = 2πm/qB e la frequenza di rotazione detta frequenza di ciclotrone è f = 1/T = qB/2πm.
Se il vettore velocità forma con la direzione del campo un angolo diverso da 0° e 90° allora lo studio del suo moto è più complicato e occorre dapprima scomporre il vettore velocità nelle due componenti, una parallela al campo e l’altra perpendicolare. La componente parallela non è influenzata dal campo B e la particella si muove nella direzione parallela con moto rettilineo uniforme. La componente perpendicolare subisce l’azione del campo magnetico e compie una traiettoria circolare. La composizione dei due moti produce un moto elicoidale cioè a elica caratterizzato anche dal passo ovvero la distanza ci cui avanza la carica nella direzione parallela al campo nell’intervallo di tempo uguale a T.
Se su una carica in moto agisce sia il campo elettrico e quello magnetico è complicato studiare il moto della carica. La forza elettrica ha la stessa direzione di quella magnetica se E e B sono perpendicolari tra loro ed entrambi perpendicolari al moto della carica. Inoltre se le forze hanno verso opposto e modulo uguale cioè qE = qvB la loro risultante è nulla. In tal caso una particella carica dotata di velocità v attraverserebbe la regione senza subire alcune deviazione. Dalla relazione qE = qvB si ricava il modulo della velocità v = E/B.

L’induzione elettromagnetica

Vediamo alcuni semplici esperimenti sulle correnti indotte:

Il moto rettilineo uniforme di una spira che si muove con velocità v perpendicolare alle linee del campo magnetico uniforme B. Si possono osservare i seguenti comportamenti: finche la spira rimane completamente all’interno della regione dello spazio in cui esiste il campo magnetico non si rileva alcuna corrente indotta. Appena la spira comincia ad entrare o ad uscire dalla regione in cui si ha il campo magnetico si rileva nel circuito una corrente indotta. Quando la spira esce completamente o entra completamente la corrente cessa immediatamente. I versi della corrente sono opposti a seconda che la sia esca o entri nel campo magnetico.
Se poniamo in rotazione con velocità costante una spira all’interno di un campo magnetico uniforme si genera in essa una corrente alternata: una corrente che inverte il verso di circolazione ogni mezzo giro della spira. Se la spira ferma la corrente si interrompe. Invertendo il verso di rotazione della spira si inverte anche il verso iniziale della corrente.
Proviamo ora a tenere ferma la spira e a muovere un magnete verso di essa: si registra immediatamente la presenza di una corrente indotta. Analogamente, si genera corrente al’interno della spira allontanando il magnete, ma il verso della corrente è opposto. Gli stessi risultati si ottengono se è la spira a muoversi relativamente al magnete.
E’ possibile produrre correnti indotte anche senza movimenti relativi di circuiti e magneti. E’ sufficiente far passare una corrente variabile in una spira o in un solenoide per osservare una corrente indotta in un'altra spira parallela a essa. La corrente variabile nell’anello genera un campo magnetico variabile e quindi potremo dire che un campo magnetico variabile genera una corrente indotta in una spira attraversata dallo steso campo magnetico. Se la corrente nella prima spira diventa costante non si ha più corrente indotta nella seconda spira.

Immaginiamo un circuito quadrato con un lato mobile AC in moto con velocità v immerso in un campo magnetico perpendicolare verso l’alto. Sugli elettroni del tratto AC agisce la forza di Lorentz diretta da A verso C (ricorda che la carica dell’elettrone è negativa) e quindi essi circolano nel circuito in senso antiorario. Si genera cosi corrente indotta.
Possiamo anche immaginare che gli elettroni si muovano a causa di un campo elettrico di intensità E = F/q = qvB/q = vB diretto da C ad A. Oppure indicando con l la lunghezza di AC possiamo pensare che gli elettroni si muovano come se tra i punti A e C ci fosse una differenza di potenziale ΔV = Bvl.
Nell’esperimento 1 la forza di Lorentz agisce su tutti lati della spira: nei lati paralleli non si produce corrente, nell’altro lato perpendicolare del circuito si genera una corrente in verso opposto. Per questo quando l’altro lato che chiameremo DE è esterno al campo magnetico, mentre AC è immerso nel campo avremo una corrente che si muove in senso orario (si genera corrente solo in AC). Se sia il lato DE che AC sono immersi nel campo non si genera corrente perché i due lati subiscono forze opposte che si annullano. Se solo il lato DE è immerso nel circuito avremo corrente in senso antiorario perché gli elettroni che si muovono sono quelli del tratto DE.
Possiamo arrivare a dire che all’interno di un circuito elettrico si genera corrente indotta solo quando varia per qualunque motivo il flusso del campo magnetico attraverso la superficie delimitata dal circuito stesso.
L’unità di misura del flusso è il weber Wb che è 1 tesla per un metro quadrato.
Consideriamo la variazione di flusso che attraversa la superficie della spira anche detto flusso concatenato alla spira ΔΦ = BΔs = BlvΔt. Se consideriamo una variazione di flusso nell’unità di tempo Δt avremo ΔΦ/Δt= Blv è come la variazione di potenziale di prima.
Non essendoci nel circuito indotto punti tra i quali calcolare una differenza di potenziale si preferisce esprimere la relazione in termini di una forza elettromotrice o fem che sarebbe fem = ΔΦ/Δt= Blv.
L’equazione è nota come legge di Faraday e si può enunciare come: ogni volta che in un circuito varia il flusso concatenato di un campo magnetico, ossia un flusso cioè che attraversa la superficie delimitata dal circuito, si produce in esso una forza elettromotrice.
Possiamo anche calcolare la corrente indotta che attraversa il circuito i = ΔΦ/RΔt
Nell’esperimento 4 non è una forza magnetica che genera la corrente indotta, ma un campo elettrico.
Supponiamo che in una regione cilindrica dello spazio esista un campo magnetico che abbia direzione e verso costanti, ma intensità variabile, con velocità di variazione costante nel tempo, generando cosi un campo magnetico indotto di modulo costante. Se nella regione è presente un circuito possiamo rilevare una corrente indotta. Se non abbiamo il circuito abbiamo comunque il campo elettrico. Il lavoro compiuto dal campo per spostare una carica q lungo una circonferenza all’interno del campo magnetico è L = q ∙ fem. Ma il lavoro può esser espresso come forza per spostamento ed essendo la forza qE e lo spostamento la circonferenza 2πr abbiamo L = qE2πr.
Eguagliando le due equazione possiamo dire che la fem = 2πrE. Il secondo membro dell’equazione esprime la circuitazione del vettore campo elettrico indotto che è diversa da 0 lungo una linea chiusa quindi il campo elettrico indotto non è un campo conservativo e non è possibile definire un’energia potenziale e un potenziale elettrico.
La corrente indotta genera a sua volta un campo magnetico:il verso della corrente indotta è tale da generare un campo magnetico che si oppone alla variazione del flusso del campo magnetico esterno che ha generato la corrente indotta. Questa è la legge di Lenz.

Autore: Federico Ferranti

fonte: http://www.riassuntiliceo.altervista.org/quintof/fis1.doc

fonte: http://www.riassuntiliceo.altervista.org/quintof/fis2.doc

fonte: http://www.riassuntiliceo.altervista.org/quintof/fis3.doc

fonte: http://www.riassuntiliceo.altervista.org/quintof/fis4.doc

fonte: http://www.riassuntiliceo.altervista.org/quintof/fis6.doc

fonte: http://www.riassuntiliceo.altervista.org/quintof/fis7.doc

fonte: http://www.riassuntiliceo.altervista.org/quintof/fis9.doc

fonte: http://www.riassuntiliceo.altervista.org/quintof/fis10.doc

fonte: http://www.riassuntiliceo.altervista.org/quintof/fis11.doc

fonte: http://www.riassuntiliceo.altervista.org/quintof/fis13.doc

fonte: http://www.riassuntiliceo.altervista.org/quintof/fis14.doc

Fisica riassunti