Geometrie non euclidee

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le Geometrie non Euclidee

Le origini della geometria in Grecia

Talete di Mileto (ca. 625-547 a.C.)
Nascita di scienza e filosofia
Geometria come scienza astratta: ordine razionale delle conoscenze geometriche, regole pratiche e
formule empiriche tramandate da Babilonesi ed Egizi

Pitagora di Samo (ca. 570-495 a.C.)
Visse a Samo, in Egitto e a Crotone
Geometria chiave di lettura della natura
Incommensurabilità della diagonale del quadrato rispetto ai lati (irrazionalità di )

V secolo a.C.
Parmenide e Zenone di Elea
Paradossi dell’infinito. Discorso logico-matematico come attività mentale svincolata da realtà.
Ragionamento per assurdo
Pericle
Massimo splendore di Atene. Organizzazione democratica della polis
Sofisti
Sviluppo della dialettica come scienza dell’argomentazione
Socrate (seconda metà del secolo)
Dialogo come strumento di conoscenza
Platone (ca.428-348 a.C.)
Il filosofo più amato dai matematici puri

IV secolo a.C.
Aristotele
Sistema filosofico organizzato, inizia lo studio della logica.
Alessandro Magno
Regni ellenistici

Euclide (ca.330-275 a.C.)

Euclide opera ad Alessandria (d’Egitto). Intorno al 300 a.C. scrive gli Elementi, come summa del
sapere matematico dell’epoca. È uno dei massimi successi editoriali di tutti i tempi. Si ritiene che
Euclide, insegnante presso il Museo di Alessandria, istituto di istruzione superiore voluto da
Tolomeo I eccellesse soprattutto nella didattica, piuttosto che nella ricerca. Infatti nella sua opera
non vi sono molte conoscenze nuove, ma vi è una sistemazione di una chiarezza notevole di quelle
già disponibili. Inoltre nella sua opera non vengono trattate le conoscenze all'epoca ritenute più avanzate, come la teoria delle coniche, ma solo quelle considerate elementari (da cui il titolo del
libro). Vediamone alcuni tratti essenziali. Per prima cosa, gli Elementi sono stati classificati come
un sistema assiomatico materiale (in contrasto con i sistemi assiomatici formali).
Sistemi assiomatici materiali
1) Si introducono i termini tecnici fondamentali del discorso e se ne chiarisce il significato (termini primitivi)
2) Elenco di enunciati primari (detti assiomi o postulati) che riguardano i termini primitivi e che sono ritenuti veri
rispetto alle definizioni date in 1).
3) Tutti gli altri termini tecnici sono definiti sulla base dei termini già introdotti.
4) Tutti gli altri enunciati sono dedotti logicamente da enunciati già accettati o postulati e sono detti teoremi.
Gli Elementi sono suddivisi in tredici libri o capitoli, dei quali i primi sei riguardano la geometria
piana elementare, i tre successivi la teoria dei numeri, il libro X gli incommensurabili, gli ultimi tre
soprattutto la geometria solida.
Definizioni
I.        Punto è ciò che non ha parti.
II.       Linea è lunghezza senza larghezza.
III.      Estremi di una linea sono punti.
IV.      Linea retta è quella che giace ugualmente rispetto ai suoi punti.
V.        Superficie è ciò che ha soltanto lunghezza e larghezza.
VI.       Estremi di una superficie sono linee.
VII.      Superficie piana è quella che giace ugualmente rispetto alle rette su di essa.
VIII.    Angolo piano è l'inclinazione reciproca di due linee su un piano, le quali si incontrino fra
loro e non giacciano in linea retta
IX.       Quando le linee che comprendono l'angolo sono rette, l'angolo si chiama rettilineo.
X.        Quando una retta innalzata su una retta forma gli angoli adiacenti uguali fra loro, ciascuno
dei due angoli uguali è retto e la retta innalzata si chiama perpendicolare a quella su cui è
innalzata
XI.       Angolo ottuso è quello maggiore di un retto.
XII.     Angolo acuto è quello minore di un retto.
XIII.    Termine è ciò che è estremo di qualche cosa.
XIV.     Figura è ciò che è compreso da uno o più termini.
XV.      Cerchio è una figura piana compresa da un'unica linea [che si chiama circonferenza] tale
che tutte le rette, le quali cadano sulla linea, a partire da un punto fra quelli che giacciono
internamente alla figura, sono uguali fra loro.
XVI.     Quel punto si chiama centro del cerchio.
XVII.    Diametro del cerchio è una retta condotta per il centro e terminata da ambedue le parti dalla
circonferenza del cerchio, la quale retta taglia anche il cerchio per metà.
XVIII.    Semicerchio è la figura compresa dal diametro e dalla circonferenza da esso tagliata. E
centro del semicerchio è quello stesso che è anche centro del cerchio.
XIX.      Figure rettilinee sono quelle comprese da rette, vale a dire: figure trilatere quelle comprese
da tre rette, quadrilatere quelle comprese da quattro e multilatere quelle comprese da più di
quattro rette.
XX.        Delle figure trilatere è triangolo equilatero quello che ha i tre lati uguali, isoscele quello
che ha soltanto due lati uguali e scaleno quello che ha i tre lati disuguali.
XXI.       Infine, delle figure trilatere è triangolo rettangolo quello che ha un angolo retto,
ottusangolo quello che ha un angolo ottuso e acutangolo quello che ha i tre angoli acuti.
XXII.     Delle figure quadrilatere è quadrato quella che è insieme equilatera e ha gli angoli retti,
rettangolo quella che ha gli angoli retti ma non è equilatera, rombo quella che è equilatera
ma non ha gli angoli retti, romboide quella ha i lati e gli angoli opposti uguali fra loro, ma
non è equilatera né ha gli angoli retti. E le figure quadrilatere oltre a queste si chiamano
trapezi.
XXIII.   Parallele sono quelle rette che essendo nello stesso piano e venendo prolungate
illimitatamente dall'una e dall'altra parte, non si incontrano fra loro da nessuna delle parti.

Nozioni comuni (proprietà ritenute vere per ogni genere di grandezze)

I.           Cose che sono uguali a una stessa sono uguali anche fra loro.
II.          E se cose uguali sono addizionate a cose uguali, le totalità sono uguali.
III.        E se da cose uguali sono sottratte cose uguali, i resti sono uguali.
IV.        E se cose uguali sono addizionate a cose disuguali, le totalità sono disuguali.
V.          E doppi di una stessa cosa sono uguali tra loro.
VI.       E metà di una stessa cosa sono uguali fra loro.
VII.      E cose che coincidono fra loro sono uguali.
VIII.     E il tutto è maggiore della parte.

Postulati (proprietà ritenute vere per le grandezze geometriche)

I.           Risulti postulato: che si possa condurre una linea retta da un qualsiasi punto a ogni altro
punto.
II.         E che una retta terminata si possa prolungare continuamente in linea retta.
III.       E che si possa descrivere un cerchio con qualsiasi centro e ogni distanza.
IV.       E che tutti gli angoli retti siano uguali fra loro.
V.         E che, se una retta venendo a cadere su due rette forma gli angoli interni e dalla stessa parte
minori di due retti, le due rette prolungate illimitatamente verranno a incontrarsi da quella
parte in cui sono gli angoli minori di due retti.

GLI SVILUPPI NELLA STORIA

Il V postulato suscitò subito perplessità nei matematici, che non lo riconoscevano altrettanto
naturale e costruttivo degli altri postulati.
Lo stesso Euclide evitò di usare il V postulato nelle dimostrazioni, quando era possibile utilizzare solo i primi quattro, ad indicare che, molto probabilmente, cercò a lungo di dimostrarlo sulla base degli altri quattro e, non essendoci riuscito, lo inserì poi fra gli altri.
Esaminiamo ora la prima parte del I libro degli Elementi.
Le prime quattro proposizioni contenute in tale parte costituiscono una specie di prolungamento dei postulati e riguardano la costruzione di un triangolo equilatero di dato lato, il trasporto e la sottrazione di segmenti e il I criterio di uguaglianza dei triangoli. Nelle proposizioni 5 e 6 si dimostra che gli angoli alla base di un triangolo isoscele sono uguali e il suo inverso.
Le proposizioni 7 e 8 costituiscono il III criterio di uguaglianza dei triangoli.
Nelle proposizioni 9 e 10 si danno le costruzioni della bisettrice di un angolo e del punto medio di un segmento.
Nelle proposizioni 11 e 12 si dà la costruzione della perpendicolare da un punto ad una retta ( a seconda se il punto appartiene o non appartiene alla retta ),mentre nella 13 si dimostra che la somma di due angoli adiacenti è uguale a due angoli retti.
La proposizione 14 afferma che, se la somma di due angoli consecutivi è due retti, allora gli angoli sono adiacenti.
La proposizione 15 afferma che gli angoli opposti al vertice sono uguali.
La proposizione 16 afferma che in triangolo un angolo esterno è maggiore degli angoli interni non adiacenti.
La proposizione 17 afferma che in un triangolo la somma di due angoli è minore di due retti.
Le proposizioni 18 e 19 affermano che in un triangolo a lato maggiore è opposto angolo maggiore e viceversa.
Le proposizioni da 20 a 25 riguardano le relazioni fra lati ed angoli di un triangolo.
La proposizione 26 è il II criterio di uguaglianza dei triangoli.
Le successive proposizioni cominciano ad occuparsi delle rette parallele:
Proposizione 27: Se due rette qualsiasi tagliate da una trasversale formano con quest’ultima angoli alterni interni uguali, le due rette sono parallele.
Proposizione 28: Se due rette qualsiasi, tagliate da una trasversali formano angoli corrispondenti uguali o angoli coniugati interni supplementari, allora le rette sono parallele.

Nella dimostrazione delle prime 28 proposizioni non si è mai fatto ricorso al V postulato, esso viene impiegato per la prima volta nella proposizione 29 che risulta l’inversa della proposizione 27.
Proposizione 29: Una retta trasversale forma con due rette parallele angoli alterni interni uguali, angoli corrispondenti uguali, angoli coniugati interni supplementari.
Euclide ricavò dal V postulato, nella proposizione 30, il seguente teorema, che è equivalente al postulato ed è stato usato storicamente per i tentativi di dimostrazione dello stesso:

I primi critici di Euclide cercarono di dimostrare il V postulato in base ai quattro precedenti, ritenendolo un punto logicamente debole della costruzione euclidea.

Proclo (412-485 dC)

Nei suoi tentativi giunse soltanto a sostituirlo con vari postulati equivalenti.
Egli sosteneva che l’affermazione secondo cui le due rette, dato che convergono, si incontreranno in un punto se prolungate, era possibile ma non necessaria e portò a favore della sua ipotesi l’esempio di un ramo di iperbole che si avvicina al suo asintoto senza mai incontrarlo. Proclo affermava: “ E’ quindi chiaro che dobbiamo cercare una dimostrazione del presente teorema e che esso è alieno dal carattere speciale dei postulati ”.

Per oltre 2000 anni alcuni tra i migliori matematici, a partire da Proclo stesso e da Tolomeo, tentarono di dimostrare il V postulato di Euclide
.
John Wallis (1616-1703)

Fu il più grande matematico inglese prima di Newton. Wallis non cercò di dimostrare il V postulato in geometria assoluta ma propose un nuovo assioma, che riteneva più plausibile di quello delle parallele e dimostrò quest’ultimo a partire dal nuovo assioma e da quelli di geometria assoluta.

Postulato di Wallis: Dato un triangolo qualsiasi ABC e dato un qualsiasi segmento DE, esiste un triangolo DEF, avente DE come uno dei lati, che è simile al triangolo ABC

Si intende ovviamente che triangoli simili sono triangoli i cui vertici possono essere messi in corrispondenza biunivoca in modo che gli angoli corrispondenti siano congruenti tra loro. Purtroppo il tentativo di Wallis è fallito: non c’è alcuna ragione per considerare il suo postulato più plausibile di quello di Euclide. In realtà si può dimostrare che essi sono logicamente equivalenti (cioè che ciascuno implica l’altro)
Girolamo Saccheri (1667-1773)

Un grande passo avanti fu fatto dal gesuita italiano Girolamo Saccheri anche se è bene ricordare che egli non fece altro che riproporre uno studio sul quadrilatero elaborato dal poeta persiano Omar Khayyam e ripreso successivamente da Nasir Eddin, sopraffine matematico arabo del XIII secolo.
Saccheri cercò di dimostrare il V postulato a contrariis dicendo: sia questo postulato ciò che bisogna dimostrare; si assuma come punto di partenza la negazione di esso; se questa negazione, nel corso del procedimento dimostrativo, si distrugge da sé, essa risulterà falsa e quindi il postulato, che costituisce il suo contrario, risulterà vero.
Seguiamo, a grandi linee, il ragionamento che Saccheri ha esposto nell'opera "Euclide emendato da ogni macchia" (Euclides ab omni naevo vindicatus).
Sia un segmento AB; dagli estremi si elevino due segmenti perpendicolari di uguale grandezza tra loro, AC e BD; si congiunga C con D. Gli angoli 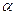saranno anch'essi uguali tra loro (basta considerare le coppie di triangoli congruenti ABC e ABD e successivamente la coppia di triangoli ADC e BDC che risultano anch'essi congruenti).
Ma come saranno questi angoli?

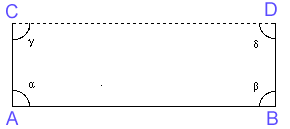
Tre sono i casi possibili:

gli angoli al vertice sono retti.
gli angoli al vertice sono ottusi.
gli angoli al vertice sono acuti.

Volendo dimostrare il primo caso, che è poi il caso della geometria euclidea, Saccheri cercò di dimostrare che gli altri due conducono a contraddizioni. Riuscì a trovare che il caso 2) porta ad una contraddizione: se gli angoli al vertice fossero ottusi, la somma degli angoli del quadrilatero sarebbe maggiore di 360°, contraddicendo il teorema che afferma che la somma degli angoli interni di un quadrilatero convesso è al più 360°. Benché si occupasse della questione con grande accanimento, non fu in grado di dimostrare che l’ipotesi 3) è contraddittoria. Alla fine affermò deluso che l’ipotesi dell’angolo acuto era assolutamente falsa, semplicemente perché ripugnante per la natura della linea retta. Nonostante non se ne fosse reso conto, Saccheri aveva scoperto la geometria non-euclidea.

Johann Heinrich Lambert (1728-1777)

Johann Heinrich Lambert studiò quadrilateri con almeno tre angoli retti, che adesso sono noti con il suo nome. Dedusse inoltre molte proposizioni non-euclidee dall’ipotesi dell’angolo acuto ma, a differenza di Saccheri, non affermò di aver trovato una contraddizione. Lambert dimostrò che l’ipotesi dell’angolo acuto implica che l’area di un triangolo è proporzionale al suo difetto angolare e ricavò che questa ipotesi corrisponde alla geometria su una sfera di raggio immaginario.

Luigi Lagrange (1736-1813)

Luigi Lagrange ,matematico italiano

, intuí la possibilità di ricavare geometrie "diverse" da quella euclidea; vittima del pregiudizio comune, non osò comunicare i suoi risultati, perché avrebbe dovuto sostenere pubblicamente che ci sono piú geometrie "vere", il che gli sembrava scandaloso.
Bisognava arrivare alla consapevolezza che non esiste una geometria "vera", ma che ogni geometria è "vera" se non contraddittoria, nei procedimenti e nei risultati, con l'ipotesi assunta.

Adrien-Marie Legendre(1752-1833)

Adrien-Marie Legendre ebbe il merito di stimolare l’interesse per i problemi concernenti il V postulato, soprattutto per la sua importante posizione accademica e per la semplicità con cui nei suoi Elements de géometrié presentò i suoi risultati anche se non furono molto diversi da quelli già ottenuti da Saccheri e da Lambert.

Karl Friedrich Gauss (1777-1855)

Karl Friedrich Gauss è considerato il primo matematico giunto alla precisa e chiara concezione di una geometria indipendente dal quinto postulato, ma egli non pubblicò i risultati raggiunti, per non suscitare le proteste e le risa di coloro che non sarebbero stati in grado di valutare tale scoperta.
Dopo un iniziale tentativo di dimostrare il quinto postulato, Gauss arrivò (1831) gradualmente alla convinzione che esistesse una geometria che, pur non accettando il quinto postulato, non avesse nulla di contraddittorio, ma egli era convinto che la geometria ( a differenza dell’algebra) non potesse costituirsi come scienza puramente a priori, ma che necessitasse anche di una corretta intuizione dello spazio esterno.
A causa della discrezione con cui Gauss mosse questi primi, seppur tanto sicuri passi su un terreno così pericoloso e ignoto, tutto l'onore della scoperta venne tributato poco dopo a due giovani matematici che, all'insaputa uno dell'altro ed in lontani paesi, giunsero quasi contemporaneamente ad analoghi risultati: l'ungherese Janos Bolyai (Kolosvàr 1802-Marosvàsàrhely 1860) ed il russo Nicolaj Ivanovic Lobacevskij (Makarèv 1793-Kazan' 1856).

Nicolaj Ivanovic Lobacevskij (1793-1856)

Lobacevskij fu detto "il Copernico della geometria" perché come Copernico riuscì con la sua teoria eliocentrica del sistema planetario a far cadere una teoria (quella geocentrica di Tolomeo) che durava da diversi secoli, così egli riuscì a far cadere una teoria (la geometria euclidea) che per duemila anni era stata considerata l'unica possibile.
Si mise così in crisi la certezza che la geometria euclidea fosse l'unica ad avere validità sia sul piano dell'esperienza ordinaria, sia sul piano logico.
La nuova geometria si otteneva assumendo tutti gli assiomi della geometria assoluta e sostituendo il postulato delle parallele con la sua negazione, cioè con il seguente

Come è possibile costruire le due rette parallele?.

In un piano si considerino una retta r ed un punto P che non appartiene alla retta.
Ora si faccia ruotare in uno dei due versi la perpendicolare n tracciata da P ad r. Il punto di intersezione si "allontana" lungo la retta r finché il punto di intersezione cessa di presentarsi da quella parte e, procedendo ulteriormente, compare dall'altra. Quanto è "grande" l'intervallo in cui la retta non interseca più la r da una parte ma ancora non la interseca dall'altra? Secondo il V postulato euclideo questo intervallo si riduce ad un unico elemento: la retta s che passa per P e che è perpendicolare a n. Quello che assume Lobacevskij è che l'intervallo delle rette che non intersecano r non si riduca a questo unico caso.

Le rette passanti per P che non intersecano r sono in numero infinito; sicuramente tutte quelle comprese nell’angolo α.
Le rette PL e PM rappresentano l’elemento di separazione tra la classe delle secanti e quella delle non secanti e vengono dette parallele ad r, mentre tutte le rette interne all’angolo a vengono dette iperparallele.
Ognuna delle due rette ha un proprio verso di parallelismo: e si dirà che PL è parallela ad OB e PM è parallela ad OA; inoltre ognuna di esse, pur prolungata all'infinito nel verso del parallelismo, non incontrerà mai la retta data, e la distanza da questa diminuirà infinitamente

Ognuno dei due angoli congruenti viene chiamato angolo di parallelismo al punto P rispetto alla retta r e si indica con p(x).

Fra le conseguenze dell’assioma di Lobacevskij sono degne di nota le seguenti proposizioni:

Dimostrazione:
Dato un triangolo qualsiasi ABC indichiamo con a, b, g i suoi angoli interni.

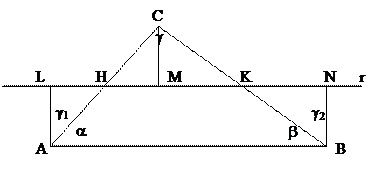
Siano H e K i punti medi dei lati AC e BC ed r la rette passante per H e K.
Siano L, M ed N le proiezioni di A, C e B, rispettivamente, sulla retta r. I triangoli ALH e HMC sono uguali per il criterio di uguaglianza dei triangoli rettangoli, come pure i triangoli CMK e KBN. Di conseguenza g1+g2=g.
Quindi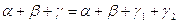
Ma il quadrilatero LNBA è un quadrilatero di Saccheri, cioè birettangolo isoscele su LN, e quindi .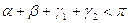

Pertanto, se non si ammette il postulato delle parallele, non esistono triangoli simili
(come era stato scoperto da Wallis alla fine del '600)

Dimostrazione:
Siano ABC e A’B’C’ due triangoli tali che .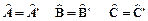
Ragioniamo per assurdo: supponiamo che i due triangoli non siano congruenti. Trasportiamo il triangolo A’B’C’ in modo che l’angolo in A e l’angolo in A’ coincidano. Si possono presentare due situazioni:
1° caso

Consideriamo la somma degli angoli nel quadrangolo B’BCC’
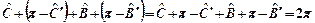assurdo
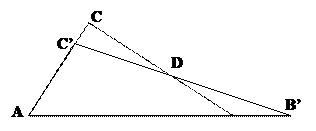2° caso

Consideriamo la somma degli angoli nel triangolo DCC’
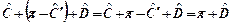assurdo, pertanto ABC e A’B’C’ sono congruenti

L’angolo di parallelismo p(x) varia in funzione del segmento PO=x ed assume tutti i valori compresi tra 0 e .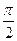

La formula forse più importante della geometria iperbolica è quella che fornisce la relazione fra l’angolo di parallelismo p(x) e la lunghezza del segmento x

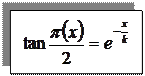
dove x è la misura del segmento PO, più x è piccolo e più l’angolo di parallelismo si approssima ad un angolo retto.
Allo stesso risultato si perviene facendo tendere k all’infinito qualunque sia x.
Il legame tra angolo di parallelismo e misura dei segmenti porta ad una unità di misura naturale per i segmenti.
Nella geometria euclidea la scelta dell’unità di misura dei segmenti è arbitraria ( per misurare un segmento va confrontato con un campione arbitrariamente scelto),mentre per gli angoli è possibile fissare un’unità di misura naturale essendo ogni angolo confrontabile con l’angolo giro.
Nella geometria iperbolica invece si può decidere che sia unitario il segmento corrispondente ad un dato angolo di parallelismo.
Se chiamiamo difetto angolare di un triangolo la differenza fra p e la somma degli angoli interni, si ha che:

(per cui segue subito che l’area di ogni triangolo è al più pK2 essendo al massimo difetto (ABC)=p).

Dopo la pubblicazione in tedesco dell’opera di Lobacevskij nel 1840 la geometria non euclidea per parecchi decenni continuò a rappresentare un aspetto marginale della matematica , fino a che essa non venne incorporata nella matematica come sua parte integrante attraverso le concezioni generali di G.F.B. Riemann ( 1826-1866)
Bernhard Riemann (1826-1866)

Riemann costruí un altro tipo di geometria, egualmente rigorosa e coerente, ipotizzando una nozione di spazio, di piano, di retta ecc. diversa da quella che era alla base del sistema euclideo.
Nel 1854 Riemann diventò Professore all’Università di Gottinga e nella sua presentazione alla facoltà tenne una dissertazione sulla storia della matematica riguardante la geometria dal titolo:
Sulle ipotesi che stanno alla base della Geometria

Il lavoro pubblicato nel 1867 forniva un nuovo modo di intendere la geometria, la presentava come un caso particolare di un nuovo concetto matematico, la varietà pluridimensionale;
La varietà pluridimensionale
, per Riemann, è l’insieme di tutte le n-ple ordinate di numeri reali.
Il piano può essere considerato una varietà bidimensionale e lo spazio una varietà tridimensionale.
Riemann dimostra che le proprietà geometriche di una varietà dipendono da un certo nuemero che Si possono distinguere le seguenti varietà:

Varietà a curvatura costante
Varietà a curvatura variabile

Le varietà a curvatura costante poi si possono classificare in base alla loro curvatura:

Varietà a curvatura costante negativa in esse vale la geometria iperbolica di Loacevskij
Varietà a curvatura costante nulla in esse vale l’ordinaria geometria euclidea
Varietà a curvatura costante positiva la cui geometria corrisponde all’ipotesi dell’angolo ottuso di Saccheri e viene anche detta Geometria ellittica.

Geometria Ellittica

La geometria ellittica può essere ottenuta modificando i primi quattro postulati di Euclide, e sostituendo il postulato delle parallele con la seguente affermazione:

Consideriamo una retta r nel piano e tracciamo due rette ad essa perpendicolari nei suoi punti A e B.
Se vale l’assioma di Riemann le due perpendicolari si devono incontrare almeno in un punto P, dato che in questa nuova geometria non esistono rette parallele. Costruiamo poi a partire da A la semiretta opposta a quella che contiene il punto P e su di essa stacchiamo il segmento AP’ uguale ad AP. Congiungiamo P con B e P’ con B. I due triangoli PAB e P’AB sono uguali in quanto hanno: PA=P’A per costruzione, BA in comune e gli angoli PAB e P’AB entrambi retti.pertanto l’angolo P’BA risulta retto essendo uguale all’angolo PBA. I tre punti B, P e P’ sono quindi allineati.

Si possono distinguere due casi:

I punti P e P’ sono distinti. Si costruisce a partire da questa ipotesi quella che viene detta geometria sferica
In questa geometria non è più valido il postulato di Euclide secondo cui per ogni coppia di punti distinti passa una ed una sola retta, infatti per P e P’ passano almeno due rette distinte

Tra le due rette P-A-P’ e P-B-P’ è racchiusa un’area finita.

.Il punto P coincide con il punto P’. Si costruisce a partire da questa ipotesi quella che viene detta geometria ellittica.
In questo caso viene però contraddetto l’assioma di ordinamento in quanto A non può stare tra P e P’ come era stato supposto per ipotesi.

Geometria sferica

Sostituiamo i primi due assiomi di appartenenza di Hilbert, con il seguente assioma:

Definiamo antipodali due punti appartenenti ad una stessa coppia.
I punti P e P’ della figura precedente sono dunque antipodali, in quanto per essi passano almeno due rette. Evidentemente si è introdotto un nuovo concetto primitivo quello di coppia di punti antipodali, oltre a quelli di punto , retta e appartenenza.

Nella geometria sferica:

Riportiamo sulla retta PA, che indicheremo con s, a partire dal punto P’ un segmento P’C=PA.
Per il punto C tracciamo la perpendicolare h alla retta s e riportiamo un segmento CD=AB.
I triangoli P’AB e P’CD sono uguali per il primo criterio. Quindi anche l’angolo PDC è retto. Costruiamo ora il punto P’’ tale che CP’’=CP’. Per i punti P’ e P’’ passano almeno due rette (P’-C-P’’ e P’-D-P’) per cui P’’ e P’ sono i due punti diametralmente opposti, cioè due punti antipodali in cui si incontrano le due rette

Poiché anche P’ e P sono punti antipodali, P deve coincidere con P’’.
Pertanto la retta è chiusa, poiché movendoci nel verso contrario ad AP abbiamo raggiunto P .

Le principali proprietà della geometria sferica sono:

Le rette sono linee chiuse di lunghezza 4d, con d= d(A,P)
Due rette si intersecano in due punti diametralmente opposti detti punti antipodali
Per ogni coppia di punti non antipodali passa una ed una sola retta
La somma degli angoli interni di un triangolo è maggiore di p
Due triangoli aventi angoli corrispondenti uguali sono uguali
L’area di un triangolo è proporzionale all’eccesso angolare, cioè alla differenza tra la somma dei suoi angoli interni e p

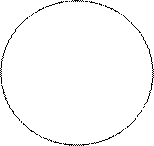La geometria sferica possiede un’interpretazione immediata nella geometria euclidea se si considera:
Il piano come insieme dei punti di punti di una superficie sferica nello spazio euclideo

Il punto come punto sulla superficie sferica

La retta come cerchio massimo della superficie sferica, cioè cerchio intersezione della superficie sferica con un qualsiasi piano passante per il centro della sfera.
In base a questo modello è relativamente intuitivo interpretare alcune delle proposizioni che abbiamo già elencato. In particolare si può verificare che:

Per un punto passano infinite rette: infatti per due punti antipodali passano infiniti cerchi massimi.
Per ogni coppia di punti distinti passa una sola retta: infatti per due punti non antipodali passa un solo cerchio massimo poiché i due punti della sfera individuano, con il centro, un unico piano che taglia sulla sfera un cerchio massimo passante per due punti.
Due rette si incontrano sempre: infatti, due cerchi massimi sono individuati da due piani passanti per il centro della sfera ed hanno quindi come intersezione una retta che taglia la sfera in due punti antipodali comuni alle due rette.

Geometria ellittica di Riemann

Le principali proprietà della geometria ellittica, di cui omettiamo la dimostrazione, sono:

Tutte le rette hanno la stessa lunghezza 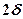(vedi fig.1)
Tutte le perpendicolari ad una retta concorrono in un punto
Se P è un punto del piano, il luogo dei punti del piano che si trovano a distanza 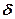da P
è una retta perpendicolare a tutte le rette passanti per P; si definisce, inoltre, polo il punto P in cui concorrono tutte le perpendicolari ad una retta r, detta retta polare del punto P.
In un triangolo rettangolo l’angolo opposto ad uno dei lati dell’angolo retto è acuto, retto o ottuso a seconda che il lato sia minore, congruente o maggiore di .
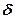La somma degli angoli interni di un triangolo è maggiore di π

Anche per la geometria ellittica è possibile costruire un modello, consideriamo un punto O dello spazio euclideo e chiamiamo stella di centro O l’insieme di tutte le rette e di tutti i piani passanti per O.
Secondo questo modello:
Il piano è l’insieme delle rette della stella di centro O.
Il punto è ogni retta della stella di centro O.
La retta è ogni piano della stella di centro O.
Con questo modello gli assiomi della geometria ellittica diventano proposizioni dimostrabili nella geometria euclidea della stella di rette e piani.
Ad esempio:

Due rette si incontrano sempre in un punto:

Infatti due rette r ed s , due piani della stella di centro O, hanno in comune il punto Oe quindihanno in comune anche una retta passante per O , cioè un punto.
Per due punti distinti passa una sola ed una sola retta:

Infatti, dati due punti A e B, cioè due rette della stella di centro O, esiste uno ed un solo piano appartenente alla stella che contiene due rette , cioè una sola retta passante per i due punti dati Ae B.

Fonte: http://www.liceomarconi.it/Progetti/progetto_ponte/non_euclid_altre_mat/geometrie_non_euclidee.doc

Geometrie non euclidee