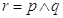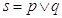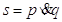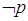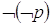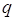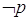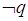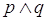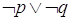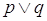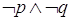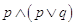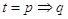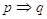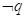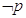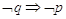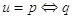Geometria razionale nozioni fondamentali
Geometria razionale nozioni fondamentali
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.
MATEMATICA C3 - GEOMETRIA
1. NOZIONI FONDAMENTALI
Geometry lesson
Photo by: kevindooley
Taken from: http://www.flickr.com/photos/pagedooley/2575606606/
License: Creative commons Attribution
1. INTRODUZIONE ALLA GEOMETRIA RAZIONALE
►1. Breve nota storica
La parola geometria deriva dal greco antico: γεωμετρία, composta da γεω (geo) che significa "terra" e da μετρία (metria) che significa "misura",che tradotto alla lettera significa “misura della terra”. Secondo una tradizione storica, durante il VI secolo a.C. alcuni matematici e pensatori greci (principalmente Talete e Pitagora) cominciarono a organizzare in maniera razionale (secondo il susseguirsi di ragionamenti logici) le conoscenze geometriche che egiziani e babilonesi avevano raggiunto nei secoli precedenti. Lo storico greco Erodoto, vissuto tra il 484 a.C. e il 425 a.C., racconta che a causa delle periodiche inondazioni del fiume Nilo gli egiziani erano costretti a ricostruire ogni anno i confini dei singoli possedimenti terrieri e in questo modo avevano sviluppato delle modalità tecniche per la misura della terra (γεωμετρία appunto). Ritrovamenti più recenti di tavolette di creta del periodo babilonese incise con caratteri cuneiformi ci fanno ritenere che la cultura babilonese possedesse già delle sofisticate conoscenze geometriche. Di certo sappiamo che nel III secolo a.C. il matematico ellenico Euclide, direttore della grande biblioteca di Alessandria in Egitto, diede una struttura razionale alle conoscenze geometriche note sino ad allora scrivendo una delle più grandi opere della cultura occidentale, gli “Elementi” (in greco Στοιχεῖα). Questa grande opera è organizzata in 13 libri, di cui i primi sei riguardano la Geometria Piana, i successivi quattro trattano i rapporti tra grandezze e gli ultimi tre riguardano la Geometria Solida. Essa prese il posto di tutti i libri precedenti sulla geometria e servì come testo fondamentale nell’antichità e nel medioevo; è stata usata come libro scolastico di geometria fino ai nostri giorni. La sua considerazione presso i Romani fu modesta, ma fu grandissima presso i Bizantini e gli Arabi. Proprio questi ultimi la reintrodussero in Europa dopo la perdita medievale, grazie alla traduzione di Abelardo di Bath (secolo XII).
Dal punto di vista della struttura logica, gli Elementi di Euclide sono organizzati a partire da cinque assiomi (nozioni comuni evidenti), cinque postulati (proposizioni che si richiede siano assunte come vere, senza dimostrazione) specifici della geometria e 23 definizioni. L’opera di Euclide è rimasta nella nostra cultura l’unico punto di riferimento per lo studio della geometria, fino a quando, contestualmente allo studio dei fondamenti delle altre branche della matematica, i matematici cercarono di dare un base più rigorosa alla geometria di Euclide. Una impostazione assiomatica più moderna venne data dal matematico tedesco David Hilbert nel libro Grundlagen der Geometrie pubblicato nel 1899, nel quale la geometria veniva fondata su ben 21 assiomi.
►2. Lo spazio fisico e la geometria
La geometria nasce come studio sistematico dello spazio fisico e delle forme che in esso si muovono. Lo spazio in cui ci muoviamo è per tutti una delle prime esperienze che facciamo a partire fin dai primi mesi di vita. I nostri sensi determinano le sensazioni che ci permettono di riconoscere le forme degli oggetti e i loro movimenti. Tuttavia le nozioni geometriche come quelle di punto, retta, rettangolo, cubo, sfera... non trovano un perfetto riscontro nella realtà fisica. Nello spazio fisico non esistono, infatti, punti e rette come li descrive la geometria, né figure a due sole dimensioni, né cubi o sfere perfette. La geometria si propone quindi di fornire un ‘modello’ ideale della realtà fisica per ciò che riguarda le forme degli oggetti e le proprietà dello spazio in cui sono immersi.
Fino alla seconda metà dell’Ottocento, matematici e filosofi sono stati sostanzialmente d’accordo nel considerare la geometria come la scienza che descriveva razionalmente le proprietà dello spazio fisico. Galileo ne Il saggiatore (1623) scriveva:
“La filosofia è scritta in questo grandissimo libro che continuamente ci sta aperto innanzi a gli occhi (io dico l'universo), ma non si può intendere se prima non s'impara a intender la lingua, e conoscer i caratteri, ne' quali è scritto. Egli è scritto in lingua matematica, e i caratteri son triangoli, cerchi, ed altre figure geometriche, senza i quali mezi è impossibile a intenderne umanamente parola; senza questi è un aggirarsi vanamente per un oscuro laberinto.”
A partire dalla seconda metà del XIX secolo i matematici si sono invece convinti che la geometria non descrive esattamente lo spazio fisico, che sono possibili più geometrie ugualmente vere dal punto di vista logico e matematico. Lo studio matematico della geometria si è allora differenziato dallo studio dello spazio fisico, e da quello dello spazio psicologico percepito dall’uomo con i suoi sensi. I matematici hanno accettato l’esistenza di diverse geometrie matematicamente possibili, si sono accontentati di costruire dei modelli astratti e hanno lasciato ai fisici la ‘scelta’ del modello che meglio si adatta a descrivere i fenomeni fisici dall’infinitamente piccolo all’infinitamente grande. La geometria allora è diventata una branca della matematica alla quale i matematici hanno cercato di dare un fondamento esclusivamente logico, indipendente dalle esperienze fisiche.
Il legame tra fisica e matematica non si è però mai rotto. Con il passare dei secoli, ci si è resi sempre più conto di quanto la “geometria” del mondo sia molto più complessa di quanto sembrasse e di come alcune nuove geometrie riescono a descrivere meglio fenomeni che con la vecchia geometria di Euclide non si riusciva a spiegare.
►3. Il metodo assiomatico, i concetti primitivi e le definizioni
La geometria, sin dai tempi di Euclide, è stata organizzata assiomaticamente, partendo cioè dalla fondamenta. Nella matematica queste fondamenta sono costituite dai concetti primitivi e dagli assiomi. Gli enti primitivi sono le nozioni che si decide di non definire. Ci si può rendere facilmente conto, infatti, che non tutto può essere definito, poiché in ogni nozione che si definisce si deve fare ricorso ad altre nozioni, le quali a loro volta devono essere definite per mezzo di altre nozioni e così via all’indietro senza che teoricamente questo processo abbia mai una fine, arrivando necessariamente ad alcune nozioni così primitive da non poter essere definite con altre nozioni più elementari. A queste nozioni non è né necessario né possibile associare alcun significato esplicito, è invece fondamentale esprimere le loro proprietà esclusivamente attraverso assiomi, cioè attraverso proprietà non dimostrabili che indicano però come gli enti primitivi devono e possono essere usati. Il matematico Hilbert utilizza tre enti primitivi - punto, linea e piano - e 21 assiomi. A partire dagli enti primitivi si danno e fanno derivare tutte le definizioni degli enti geometrici.
►4. Nozioni di logica
Assumiamo come “primitivo” il concetto base di proposizione (o “giudizio” secondo la terminologia del grande filosofo greco Aristotele): chiamiamo proposizione una frase (affermativa o negativa) a cui abbia senso associare un valore di verità (V, vero, oppure F, falso).
Per esempio, sono proposizioni logiche affermazioni del tipo “Una retta ha infiniti punti”, “2+3=10”. Non sono proposizioni logiche le frasi “1000 è un numero grande”, “il quadrato è semplice”. La prima frase esprime un’affermazione vera, la seconda un’affermazione falsa, la terza e la quarta esprimono affermazioni non valutabili oggettivamente, di queste ultime non si può dire se sono vere o false.
1 Quali delle seguenti frasi sono proposizioni logiche?
- I matematici sono intelligenti Sì No
- 12 è un numero dispari Sì No
- Pascoli è stato un grande poeta Sì No
- Pascoli ha scritto La Divina Commedia Sì No
- Pascoli ha scritto poesie Sì No
- Lucia è una bella ragazza Sì No
- Lucia ha preso 8 al compito di matematica Sì No
Bisogna tenere conto che una proposizione può essere logica in un sistema e non esserlo in un altro. La possibilità di determinare la verità di una proposizione dipende infatti dalle modalità attraverso cui si può arrivare a determinarne la verità. Per esempio la proposizione “Questo bullone è grande” in generale non è una proposizione logica ma se sappiamo che il metro di riferimento è un determinato dado allora acquisisce una valore logico perché si può stabilire se quel bullone è troppo grande o no. Quindi in generale potremmo dire che una proposizione è decidibile se nel sistema di riferimento esiste un modo per determinarne la veridicità.
La logica delle proposizioni si fonda sui seguenti tre principi della logica aristotelica:
- Il principio di identità: ogni oggetto è identico a se stesso e a nessun altro oggetto;
- Il principio di non contraddizione: una stessa proposizione non può essere contemporaneamente vera e falsa;
- Il principio del terzo escluso (“tertium non datur”): una proposizione può essere solo vera o falsa, non può assumere un diverso valore di verità.
Il corpo della geometria, come di qualunque altra teoria matematica, è costituito da proposizioni, cioè da affermazioni che riguardano gli enti geometrici e che sono vere o false.
Le proposizioni possono essere semplici affermazioni (proposizioni atomiche) oppure possono essere ottenute da una o più proposizioni elementari legate tra di loro attraverso connettivi logici (elementi linguistici del tipo “non”, “e”, “oppure”, “o … o”, “quindi”, “se … allora”, “se e solo se”). In questo caso si parla di proposizioni composte o molecolari
Per esempio, la proposizione “un triangolo ha tre lati e ha tre angoli” è composta dalle proposizioni “un triangolo ha tre lati” e “un triangolo ha tre angoli” unite dal connettivo “e”.
p |
q |
|
V |
V |
V |
V |
F |
F |
F |
V |
F |
F |
F |
F |
La congiunzione di due proposizioni si ottiene con il connettivo “e” (et, and, Ù): la proposizione r ottenuta dalla congiunzione delle proposizioni p e q, in simboli si usa scrivere 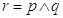 , è vera se entrambe le proposizioni p e q sono contestualmente vere, è falsa quando anche una sola delle due proposizioni è falsa. Per esprimere tutte le possibilità in maniera sintetica si usa una tabella a doppia entrata, detta tavola di verità:
, è vera se entrambe le proposizioni p e q sono contestualmente vere, è falsa quando anche una sola delle due proposizioni è falsa. Per esprimere tutte le possibilità in maniera sintetica si usa una tabella a doppia entrata, detta tavola di verità:
p |
q |
|
V |
V |
V |
V |
F |
V |
F |
V |
V |
F |
F |
F |
La disgiunzione (inclusiva) di due proposizioni si ottiene con il connettivo “o” (vel, or, Ú): la proposizione s ottenuta dalla disgiunzione di due proposizioni p e q, in simboli 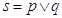 , è vera quando almeno una delle due proposizioni è vera, è falsa solo se entrambe le proposizioni sono false.
, è vera quando almeno una delle due proposizioni è vera, è falsa solo se entrambe le proposizioni sono false.
p |
q |
|
V |
V |
F |
V |
F |
V |
F |
V |
V |
F |
F |
F |
La disgiunzione esclusiva di due proposizioni si ottiene con il connettivo [o congiunzione] “o … o” (aut, xor, 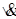 , è vera quando solo una delle due proposizioni è vera, è falsa quando le due proposizioni sono entrambe vere o entrambe false.
, è vera quando solo una delle due proposizioni è vera, è falsa quando le due proposizioni sono entrambe vere o entrambe false.
Esempio
p=”un triangolo ha tre lati” (Vera) q=”un triangolo ha tre vertici” (Vera)
r=”un triangolo ha quattro angoli” (Falsa) s=”un triangolo ha tre dimensioni” (Falsa)
Allora
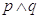 è falsa.
è falsa.Inoltre
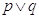 è falsa.
è falsa.Invece
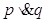 è falsa.
è falsa. La negazione (connettivo “non”, simboli non, not,  che è vera se p è falsa, viceversa è falsa se p è vera.
che è vera se p è falsa, viceversa è falsa se p è vera.
La doppia negazione equivale ad un’affermazione, cioè 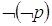 .
.
La tavola di verità è la seguente:
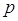 |
|
|
V |
F |
V |
F |
V |
F |
Esempio
In riferimento agli esempi precedenti, Øp e Øq sono false, mentre Ør e Øs sono vere.
È piuttosto semplice capire il meccanismo della negazione se applicata a proposizioni atomiche, spesso è meno intuitivo il valore di verità della negazione di una proposizione più complessa.
Ad esempio, la negazione di 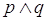 .
.
In formule: 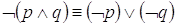 .
.
Queste uguaglianze prendono il nome di leggi di De Morgan.
La verifica si può vedere dalla seguente tavola di verità:
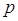 |
|
|
|
|
|
|
|
V |
V |
F |
F |
V |
F |
V |
F |
V |
F |
F |
V |
F |
V |
V |
F |
F |
V |
V |
F |
F |
V |
V |
F |
F |
F |
V |
V |
F |
V |
F |
V |
Come per le operazioni aritmetiche anche per gli operatori logici è possibile analizzarne le proprietà. Ne indichiamo qualcuna a titolo di esempio:
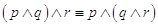 proprietà associativa della congiunzione
proprietà associativa della congiunzione
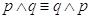 proprietà commutativa della congiunzione
proprietà commutativa della congiunzione
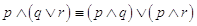 proprietà distributiva della congiunzione rispetto alla disgiunzione
proprietà distributiva della congiunzione rispetto alla disgiunzione
2 A partire dalle due proposizioni:
p = ”16 è divisibile per 2” q = “16 è divisibile per 4”
costruisci le proposizioni
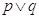 =
=
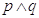 =
=
3 A partire dalle proposizioni: p=”18 è divisibile per 3” q=”18 è numero dispari”
costruisci le proposizioni di seguito indicate e stabilisci il loro valore di verità
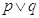 V F
V F
c) 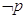 V F
V F
e) 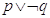 V F
V F
4 In quale delle seguenti proposizioni si deve usare la o inclusiva e in quali la o esclusiva:
- Nelle fermate a richiesta l’autobus si ferma se qualche persona deve scendere o salire.
- Luca sposerà Maria o Claudia.
- Fammi chiamare da Laura o da Elisa.
- Si raggiunge l’unanimità quando sono tutti favorevoli o tutti contrari.
La disgiunzione esclusiva 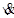 a volte non viene messa tra gli operatori logici fondamentali perché è esprimibile attraverso gli altri tre altri operatori presentati finora.
a volte non viene messa tra gli operatori logici fondamentali perché è esprimibile attraverso gli altri tre altri operatori presentati finora.
5 Verificare che date due proposizioni p e q, la proposizione composta 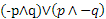 . Dimostrare poi l’equivalenza usando le tavole della verità.
. Dimostrare poi l’equivalenza usando le tavole della verità.
6 A partire dalla preposizioni: p = ”Oggi pioverà” 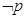 = ”Oggi non pioverà”
= ”Oggi non pioverà”
scrivere le preposizioni 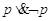 . Scrivere quindi la loro tabella della verità.
. Scrivere quindi la loro tabella della verità.
7 Scrivere le tabelle di verità delle formule
8 Qual è la negazione della frase “Ogni volta che ho preso l’ombrello non è piovuto”?
[A] Almeno una volta sono uscito con l’ombrello ed è piovuto
[B] Quando esco senza ombrello piove sempre
[C] Tutti i giorni in cui non piove esco con l’ombrello
[D] Tutti i giorni che è piovuto ho preso l’ombrello
Una proposizione che è sempre vera indipendentemente dalla verità degli elementi che lo compongono è detta tautologia. Una proposizione che è sempre falsa indipendentemente dalla verità dei suoi elementi è invece della contraddizione.
Esempi
La proposizione composta 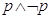 è una contraddizione in quanto è sempre falsa.
è una contraddizione in quanto è sempre falsa.
La proposizione composta 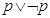 è una tautologia in quanto è sempre vera.
è una tautologia in quanto è sempre vera.
9 Costruisci le tavole di verità per le proposizioni composte
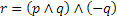
Cosa puoi dire delle proposizioni r ed s?
►5. Predicati e quantificatori
Una proposizione che fa riferimento a una proprietà o caratteristica di alcuni elementi di un insieme si chiama predicato. Le frasi formate da un predicato che ha alcuni argomenti incogniti si dicono enunciati aperti.
Per esempio, p = “x è un numero intero maggiore di 10” è un enunciato aperto.
Consideriamo ora le seguenti affermazioni:
- "Tutti gli uomini sono mortali" si riferisce a un qualsiasi essere umano;
- "Tutti i multipli di 6 sono anche multipli di 2" è vera per tutti i numeri multipli di 6;
- "Ogni numero negativo è minore di ogni numero positivo".
I predicati precedenti non riguardano un elemento specifico ma una certa quantità di elementi. I termini "tutti" e "ogni", detti quantificatori universali, indicano che una proprietà è vera per tutti gli elementi di un certo insieme. In logica matematica si usa il simbolo ", leggi "per ogni", per indicare il quantificatore universale.
Vediamo ora i seguenti predicati:
- "Esiste un numero che elevato al quadrato dà 16"
- "Alcuni numeri pari sono anche multipli di 3."
Queste affermazioni esprimono proprietà che sono vere almeno per un elemento dell'insieme di riferimento: la prima frase è vera per i numeri +4 e -4, la seconda frase è vera per i numeri 6, 12, 18, …
I termini "c'è almeno", "alcuni", "esiste almeno uno" si dicono quantificatori esistenziali e si indicano con il simbolo $, leggi "esiste".
Bisogna prestare particolare attenzione quando si negano frasi in cui compaiono i quantificatori. Per esempio la negazione di "Tutti i gatti fanno le fusa" non è "Nessun gatto fa le fusa" bensì "Non tutti i gatti fanno le fusa" che si può esprimere anche con il quantificatore esistenziale "c'è almeno un gatto che non fa le fusa".
La negazione della frase "L'anno scorso siamo stati tutti promossi" non è "L'anno scorso siamo stati tutti bocciati" ma "L'anno scorso c'è stato almeno uno di noi che non è stato promosso".
Esempio
Se si considera la proposizione p = “Tutti i quadrati hanno due diagonali”, la sua negazione è la proposizione Øp = “Non tutti i quadrati hanno due diagonali”.
Il linguaggio comune ci indurrebbe a considerare come negazione di p la proposizione “Nessun quadrato ha due diagonali”, in realtà per avere la negazione della proposizione p basta che esista almeno un quadrato che non ha due diagonali.
10 Scrivi le negazioni delle seguenti frasi che contengono dei quantificatori
- Al compito di matematica eravamo tutti presenti.
- Ogni giorno il professore ci dà sempre compiti per casa.
- Ogni giorno Luca vede il telegiornale
- Tutti i miei familiari portano gli occhiali
►6. L’implicazione
Nel linguaggio matematico sono comuni proposizioni del tipo “Se p allora q”. Ad esempio “Se un numero è multiplo di 12 allora è multiplo di 3”. La frase precedente può essere espressa dicendo:
“Essere multiplo di 12 implica essere multiplo di 3”.
In logica frasi del tipo “Se p allora q” vengono tradotte utilizzando l’operatore infisso (ovvero interposto fra le proposizioni) 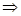 detto implicazione.
detto implicazione.
La scrittura “se p allora q” si traduce con la scrittura 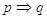 , che si legge “p implica q”.
, che si legge “p implica q”.
La proposizione p è detta antecedente, (o ipotesi) la proposizione B è detta conseguente (o tesi).
Il significato logico della proposizione 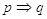 è che “tutte le volte che la proposizione p è vera allora risulta vera anche la proposizione q”. Ovvero non si dà il caso che p sia vera e q sia falsa.
è che “tutte le volte che la proposizione p è vera allora risulta vera anche la proposizione q”. Ovvero non si dà il caso che p sia vera e q sia falsa.
La tavola di verità è la seguente:
p |
q |
|
V |
V |
V |
V |
F |
F |
F |
V |
V |
F |
F |
V |
Uno degli errori logici più comuni è quello di pensare che da 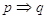 .
.
Ad esempio dall’affermazione “Se piove prendo l’ombrello” qualcuno può pensare che si possa dedurre “Se non piove non prendo l’ombrello”. Tuttavia, riflettendoci si intuisce che le due frasi non sono affatto consequenziali. Basta pensare che chi pronuncia la prima frase sta affermando che tutte le volte che piove prende naturalmente l’ombrello, ma non esclude la possibilità di prenderlo anche quando non piove (in effetti è saggio farlo se il cielo è coperto da nuvoloni neri!).
Così la frase: a) “Se x è multiplo di 12 allora è multiplo di 3”
non vuol dire: b) “Se x non è multiplo di 12 allora non è multiplo di 3”
Infatti la (a) è vera, mentre la (b) è falsa (si pensi al 6 che non è multiplo di 12 ma è multiplo di 3).
Ciò che ragionevolmente si può dedurre da 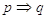 .
.
Ad esempio da:
“Se x è multiplo di 12 allora è multiplo di 3”
si può dedurre:
“Se x non è multiplo di 3 allora non è multiplo di 12”
Data l’implicazione 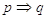 la proposizione p viene detta condizione sufficiente per q. Mentre la proposizione q viene detta condizione necessaria per p.
la proposizione p viene detta condizione sufficiente per q. Mentre la proposizione q viene detta condizione necessaria per p.
Quest’ultima espressione fa appunto riferimento al fatto che da 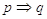 . Ossia q è necessaria per p in quanto se non è vera q non è vera neanche p.
. Ossia q è necessaria per p in quanto se non è vera q non è vera neanche p.
Calcoliamo la tavola di verità di 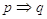
p |
q |
|
|
|
|
|
V |
V |
V |
|
F |
F |
V |
V |
F |
F |
|
V |
F |
F |
F |
V |
V |
|
F |
V |
V |
F |
F |
V |
|
V |
V |
V |
Come si vede, le due proposizioni hanno gli stessi valori di verità.
In generale, data un’implicazione 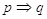 (proposizione diretta):
(proposizione diretta):
- l’implicazione
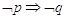 ;
; - l’implicazione
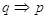 ;
; - l’implicazione
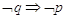 .
.
La doppia implicazione, o equivalenza logica, di due proposizioni p e q dà luogo a una proposizione u che in simboli si rappresenta 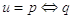 (leggasi “p se e solo se q”) che è vera se p e q sono entrambe vere o entrambe false. La tavola di verità è la seguente:
(leggasi “p se e solo se q”) che è vera se p e q sono entrambe vere o entrambe false. La tavola di verità è la seguente:
p |
q |
|
|
p Þ q |
q Þ p |
(p Þ q) Ù (q Þ p) |
V |
V |
V |
|
V |
V |
V |
V |
F |
F |
|
F |
V |
F |
F |
V |
F |
|
V |
F |
F |
F |
F |
V |
|
V |
V |
V |
L’operatore 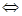 e la proposizione (p Þ q) Ù (q Þ p).
e la proposizione (p Þ q) Ù (q Þ p).
L’equivalenza logica è un relazione di equivalenza, infatti verifica le seguenti proprietà
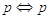 riflessiva
riflessiva- se
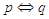 simmetrica
simmetrica - se
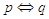 transitiva.
transitiva.
In matematica si usa spesso l’espressione “p è condizione necessaria e sufficiente per q”. Per esempio “Condizione necessaria e sufficiente affinché un numero sia divisibile per 3 è che la somma delle sue cifre sia divisibile per 3”. Il significato della frase è che “p è sufficiente per q” e inoltre “p è necessario per q”. In altre parole significa dire che 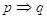 . Nel caso dell’esempio, “se un numero è divisibile per 3 allora la somma delle sue cifre è divisibile per 3” e vale anche l’implicazione inversa “se la somma delle cifre di un numero è divisibile per 3 allora il numero stesso è divisibile per 3”.
. Nel caso dell’esempio, “se un numero è divisibile per 3 allora la somma delle sue cifre è divisibile per 3” e vale anche l’implicazione inversa “se la somma delle cifre di un numero è divisibile per 3 allora il numero stesso è divisibile per 3”.
11 Sono date le frasi p = ”Mario è cittadino romano”, q = ”Mario è cittadino italiano”, scrivi per esteso le seguenti implicazioni e indica quale di esse è vera.
a) 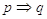 V F
V F
12 trasforma nella forma “Se… allora…” le seguenti frasi:
- Un oggetto lanciato verso l’alto ricade a terra.
- Quando piove prendo l’ombrello.
- I numeri la cui ultima cifra è 0 sono divisibili per 5.
- Per essere promosso occorre aver raggiunto la sufficienza.
13 Date le proposizioni p e q costruire la tavola di verità di 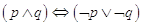 .
.
14 Scrivere la contronominale di “Tutti gli alunni che hanno avuto il debito in matematica hanno avuto almeno due valutazioni insufficienti in matematica”.
►7. I teoremi
Un teorema è una proposizione composta del tipo IÞT, cioè una implicazione tra due proposizioni, dette Ipotesi e Tesi. Dimostrare un teorema significa fare un ragionamento che permetta di concludere che la Tesi è vera avendo supposto che l’Ipotesi è vera. Nel caso in cui un teorema sia dimostrabile all’interno di una teoria, si dice che è un teorema valido. In riferimento alla terminologia usata quando abbiamo parlato dell’implicazione, chiamiamo IÞT “teorema diretto”, TÞI “teorema inverso”, ØIÞØT “teorema contrario”, ØTÞØI “teorema controinverso”, e ribadiamo l’equivalenza tra il teorema diretto ed il teorema contro inverso, nonché l’equivalenza tra il teorema contrario ed il teorema inverso, mentre in generale la validità del teorema diretto non implica la validità del teorema inverso, e viceversa. Nel caso particolare in cui vale sia IÞT sia TÞI, si scrive IÛT e si dice che Ipotesi e Tesi sono logicamente equivalenti. Più precisamente, nel linguaggio specifico delle scienze che fanno uso della logica, e quindi anche nel linguaggio della Geometria Razionale, se vale IÞT, si dice che “I è condizione sufficiente per T” e anche che “T è condizione necessaria per I”; se in particolare vale IÛT, si usa dire che “I è condizione necessaria e sufficiente per T”.
In generale incontreremo molti teoremi che vengono denominati genericamente “proposizioni”, perché il nome di “Teorema” viene tradizionalmente attribuito solo ai teoremi più importanti. Inoltre si usa chiamare “lemma” una proposizione che non ha una grande importanza di per sé, ma che è particolarmente utile per la dimostrazione di altri teoremi. Si chiama invece “corollario” un teorema importante che è una conseguenza immediata di un altro teorema.
Così come abbiamo visto che non è possibile definire tutto e che quindi bisogna assumere alcune nozioni come primitive, analogamente non è possibile dimostrare tutte le proposizioni di una teoria. Alcune proposizioni devono essere assunte come vere e costituiscono la base della dimostrazione dei teoremi; queste proposizioni si chiamano “postulati” o “assiomi”. Risulta evidente che cambiando sia pure uno solo degli assiomi cambiano anche i teoremi dimostrabili e quindi la teoria.
In generale, come abbiamo detto, dato un teorema (diretto) del tipo 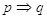 .
.
Esempio
Teorema: un triangolo che ha i lati uguali ha anche gli angoli uguali.
Il teorema si può schematizzare nel seguente modo: p = ”un triangolo ha i lati uguali”; q = ”un triangolo ha gli angoli uguali”. Il teorema enunciato è 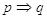 , cioè:
, cioè:
Teorema inverso: un triangolo che ha gli angoli uguali ha anche i lati uguali.
In tale esempio sono validi sia il teorema diretto sia il teorema inverso. Il fatto che uno dei due teoremi sia chiamato diretto e l’altro inverso è un fatto soggettivo, che può dipendere semplicemente dall’ordine con cui si enunciano i teoremi.
Il teorema precedente si può esporre allora nel seguente modo.
Teorema: un triangolo ha i lati uguali se e solo se ha gli angoli uguali.
►8. La deduzione
Nel paragrafo precedente abbiamo parlato in modo generico di implicazione, deduzione, dimostrazione. Facciamo ora attenzione alla differenza tra implicazione materiale e deduzione logica. L’implicazione è un’operazione tra proposizioni, mentre la deduzione è il ragionamento che costituisce la base della dimostrazione di un teorema. Per l’implicazione materiale si usa il simbolo 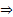 .
.
La frase “Se 5 è un numero pari, allora il triangolo ha 4 lati” è perfettamente valida ed anzi è vera, poiché la premessa (proposizione antecedente) è falsa, per cui l’implicazione è vera anche se la proposizione conseguente è falsa (si tenga presente la tavola di verità di 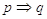 ).
).
Si noti però che la definizione di implicazione ha senso solamente se la premessa è vera, il suo ampliamento al caso in cui la premessa è falsa è motivata da ragioni di completezza della trattazione. Bisogna quindi fare attenzione ad usare l’implicazione logica quando la premessa è falsa. Teniamo comunque conto che se p è falsa allora 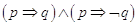 è una contraddizione, quindi una premessa falsa implica sempre una contraddizione.
è una contraddizione, quindi una premessa falsa implica sempre una contraddizione.
In realtà, la dimostrazione di un teorema non è la verifica della validità dell’implicazione, anzi è un procedimento che fa uso della validità dell’implicazione stessa. In un teorema si parte dal supporre vera l’ipotesi e si dimostra, mediante gli assiomi ed altri teoremi già dimostrati in precedenza, che anche la tesi è vera (questo se si vuole seguire il procedimento diretto). Se si vuole seguire il procedimento indiretto (o per assurdo), si suppone che la tesi sia falsa e, sempre mediante assiomi e altri teoremi già dimostrati, si arriva ad affermare che l’ipotesi è falsa (cosa che non si deve accettare).
Le principali regole del corretto ragionamento seguono alcuni schemi particolari (detti sillogismi, dal nome attribuito ad essi da Aristotele). Presentiamo qui i quattro principali sillogismi: il modus ponens, il modus tollens, il sillogismo disgiuntivo, il sillogismo ipotetico.
|
|
Modus |
|
Modus |
|
Sillogismo |
|
Sillogismo |
|
1a premessa |
|
p Þ q |
|
p Þ q |
|
p Ú q |
p Ú q |
|
p Þ q |
conclusione |
|
q |
|
Ø p |
|
p |
q |
|
p Þ r |
Suggeriamo una lettura degli schemi appena esposti:
- modus ponens: “se sappiamo che p implica q, e sappiamo che p è vera, allora possiamo concludere che anche q è vera” (metodo diretto di dimostrazione);
- modus tollens: “se sappiamo che p implica q, e sappiamo che q è falsa, allora possiamo concludere che anche p è falsa” (metodo indiretto di dimostrazione);
- sillogismo disgiuntivo: “se sappiamo che, tra p e q, almeno una delle due è vera, e sappiamo che q (rispettivamente p) è falsa, allora possiamo concludere che p (rispettivamente q) è vera”;
- sillogismo ipotetico: “se sappiamo che p implica q, e sappiamo che q implica r, allora possiamo concludere che p implica r” (proprietà transitiva dell’implicazione).
Altre regole (note come i Giudizi di Aristotele) fanno uso dei predicati e dei quantificatori, per cui riprendiamo l’Esempio 3 e vediamo di tradurre la frase “Tutti i quadrati hanno due diagonali” e la sua negazione “Non tutti i quadrati hanno due diagonali” in formule che fanno uso anche del linguaggio degli insiemi. Se chiamiamo Q l’insieme di tutti i quadrati, e chiamiamo P la proprietà dell’avere due diagonali, se x è il generico quadrato (elemento di Q), P(x) è il predicato “x gode della proprietà P”, cioè “x ha due diagonali”, la frase “Tutti i quadrati hanno due diagonali” si traduce così in simboli: "xÎQ, P(x).
La sua negazione è: “Esiste almeno un quadrato che non ha due diagonali, cioè che non gode della proprietà P”, e si traduce in simboli così: $xÎQ, ØP(x).
In quest’ultimo caso, la virgola può anche essere sostituita da una barra verticale (“|”) e si legge “tale che”.
Analogamente, una frase del tipo “Esiste almeno un numero naturale che sia divisore di 10” può scriversi come: $nÎN, D(n), dove D è la proprietà dell’essere divisore di 10 e D(n) significa che n verifica la proprietà D, cioè che n è un divisore di 10. La sua negazione è “Nessun numero naturale è divisore di 10”, ovvero “preso un qualsiasi numero naturale n, questo non gode della proprietà D” e la traduzione in simboli di tale frase è: "nÎN, ØD(n).
È il caso di inserire in uno schema queste quattro proposizioni (che corrispondono ai Giudizi di Aristotele):
A – Giudizio universale affermativo |
"xÎQ, P(x) |
I – Giudizio |
$nÎN, D(n) |
P è vera per ogni x |
D è vera per almeno un n |
||
O – Giudizio |
$xÎQ, ØP(x) |
E – Giudizio |
"nÎN, ØD(n) |
P è falsa per almeno un x |
D è falsa per ogni n |
Se chiamiamo R l’insieme degli elementi che verificano la proprietà P, e S l’insieme degli elementi che verificano la proprietà D, i quattro Giudizi si possono rappresentare graficamente nel modo seguente:

15 Completa i seguenti ragionamenti:
- Se un numero è multiplo di 10 allora è pari; il numero n non è pari quindi … … … …
- Se il sole tramonta fa buio; il sole è tramontato quindi … … … … … … … … … … … …
►9. La dimostrazione
Tenendo conto di quanto detto precedentemente, dimostrare che I→T significa fare un ragionamento che permetta di concludere che la tesi T è vera avendo supposto che l’ipotesi I è vera.
Quando attraverso un ragionamento logico, e cioè attraverso una catena di implicazioni del tipo I→A→B→ … →T, si riesce a dedurre la verità di una proposizione Ta partire dalla verità di una proposizione I, si dice che si è data una dimostrazione diretta del teorema I→T (attraverso le regole del modus ponens e del sillogismo ipotetico). Le regole da seguire sono state in parte illustrate quando si è parlato di deduzione.
Un teorema può anche essere dimostrato per assurdo, o con metodo indiretto, che consiste nel partire dalla negazione di T e, attraverso una catena di implicazioni, arrivare alla negazione di I o, in generale, ad una contraddizione.
Esistono altri metodi di dimostrazione, di cui eventualmente si parlerà più diffusamente qualora si dovesse ricorrere ad essi. Per ora ci limitiamo a citarne un paio: dimostrazione per induzione e dimostrazione mediante esempio o controesempio.
La dimostrazione per induzione si usa in particolare quando vogliamo dimostrare una proprietà generale che vale per molte categorie di figure ma che non si può esprimere in maniera unica per tutte le categorie (ad esempio una proprietà che vale per tutti i poligoni ma che dipende dal numero dei lati, come l’estensione dei criteri di congruenza dei triangoli a poligoni di più lati).
Si usa invece un esempio quando bisogna dimostrare che una certa proprietà vale per almeno un oggetto del nostro studio o un controesempio per dimostrare che una proprietà non vale per tutti gli oggetti in esame.
Per fornire alcuni esempi di dimostrazione, avremmo bisogno di fissare prima i concetti di base e gli assiomi da cui partire, per cui rinviamo la questione al prossimo paragrafo.
Ma a cosa serve studiare la dimostrazione di un teorema? Perché non ci limitiamo ad elencare i teoremi? Per molte applicazioni basta in effetti conoscere il teorema e a volte anche soltanto la formula risolutiva. Tuttavia studiando le dimostrazioni si impara a dimostrare e quindi si impara a creare nuova matematica. Un altro importante vantaggio è che la dimostrazione spiega perché il teorema è vero e permette di scoprire la struttura nascosta nelle definizioni e nei teoremi. Quando si studia una dimostrazione non bisogna limitarsi a leggerla e a impararla a memoria, occorre leggerla attivamente, ponendo attenzione su cosa si fa e cercando di anticipare i passaggi. Se un passaggio non è chiaro bisogna prima tornare indietro per capire come ci si è arrivati e poi si cerca di capire il perché l’autore ha messo quel passaggio. In generale, una dimostrazione va letta più volte smettendo solo quando si è compresa a fondo.
16 Dimostra con un controesempio che non è vera l’affermazione “Tutti i multipli di 3 sono dispari”.
17 Nel teorema “Il quadrato è anche rettangolo” esplicitare l’ipotesi e la ‘tesi’. Enunciare il teorema contrario. Trova un contro esempio che dimostra che il teorema contrario è falso.
18 Dimostra per assurdo il teorema “Se un numero non è divisibile per 2 allora non è divisibile per 10”.
2. GLI ENTI FONDAMENTALI
►1. Concetti primitivi
In questo paragrafo diamo un cenno del sistema assiomatico della geometria razionale facendo riferimento principalmente all’impostazione assiomatica di Hilbert.
Sono concetti primitivi per la geometria il punto, la retta e il piano. Di essi non si dà una definizione e costituiscono la base per definire tutti gli altri enti della geometria.
Oltre a questi tre enti primitivi occorre poi assumere l’esistenza di tre relazioni primitive tra gli enti geometrici: giacere su, stare fra, essere congruente a. Queste relazioni permettono di stabilire dei legami tra gli enti geometrici, per esempio: “un punto giace su una retta”, “un punto sta fra altri due punti”, “un segmento è congruente a un altro segmento”, …
Esiste una simbologia convenzionale condivisa dagli studiosi per indicare questi enti:
- per indicare un punto usiamo una lettera maiuscola, A, B, C, …;
- per indicare una retta usiamo una lettera minuscola, a, b, c, …;
- per indicare un piano usiamo una lettera greca:
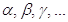 .
.
Ricordiamo l’alfabeto greco, per gli studenti che hanno poca familiarità con esso:
Lettere greche minuscole:  (o mega).
(o mega).
Lettere greche maiuscole:  .
.
Per il simbolo di congruenza si usa 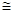 .
.
Degli enti fondamentali Euclide aveva dato le seguenti definizioni:
- Punto è ciò che non ha parti.
- Linea è lunghezza senza larghezza.
- Superficie piana è quella che giace ugualmente rispetto alle rette su di essa.
Le definizioni in questo caso sono utili per farci un’idea intuitiva di essi. Tuttavia, come è già stato detto in precedenza, e da quanto si intuisce osservando le definizioni euclidee, per definire il punto si utilizza la nozione di parte: punto è ciò che non ha parti. Occorrerebbe quindi definire che cosa è una parte. Ma per definire un parte avremmo bisogno di altre nozioni di partenza, in un procedimento senza fine. Per questo motivo nell’impostazione assiomatica moderna si preferisce non dare la definizione dei tre enti primitivi e ‘definirli implicitamente’ attraverso le proprietà di cui godono. Ciò significa che si preferisce dare maggiore importanza a come essi si comportano e cosa possiamo fare con essi, piuttosto che descrivere cosa sono.
Dal punto di vista della rappresentazione grafica si usano le seguenti convenzioni:

Figura 1. Rappresentazione grafica degli enti fondamentali della geometria.
►2. Postulati
Un postulato, o assioma, è una proposizione, spesso intuitiva, evidente ma non dimostrata, ammessa come vera in quanto necessaria per costruire poi le dimostrazioni dei teoremi.
Euclide nei suoi Elementi aveva individuato un gruppo di cinque assiomi, che riguardano le nozioni comuni e quindi non fanno riferimento alla geometria, e un gruppo di cinque postulati che riguardano proprietà geometriche.
Assiomi di Euclide
- Cose che sono uguali a una stessa cosa sono uguali anche tra loro.
- Se cose uguali sono addizionate a cose uguali, le totalità sono uguali.
- Se da cose uguali sono sottratte cose uguali, i resti sono uguali.
- Cose che coincidono fra loro sono uguali.
- Il tutto è maggiore della parte.
Postulati di Euclide
- Si possa condurre una linea retta da un qualsiasi punto ad ogni altro punto.
- Un segmento si possa prolungare indefinitamente in linea retta.
- Si possa descrivere un cerchio con qualsiasi centro e qualsiasi raggio.
- Tutti gli angoli retti siano uguali tra loro.
- Se una retta che taglia due rette forma dallo stesso lato angoli interni la cui somma è minore di due angoli retti, prolungando illimitatamente le due rette, esse si incontreranno dalla parte dove i due angoli sono minori di due retti.
 Nell’impostazione assiomatica moderna di Hilbert, gli assiomi hanno la funzione di definire implicitamente gli enti primitivi, cioè di fissare le proprietà alle quali questi enti devono soddisfare. Hilbert aggiunge inoltre altri assiomi che Euclide stesso non aveva esplicitato chiaramente.
Nell’impostazione assiomatica moderna di Hilbert, gli assiomi hanno la funzione di definire implicitamente gli enti primitivi, cioè di fissare le proprietà alle quali questi enti devono soddisfare. Hilbert aggiunge inoltre altri assiomi che Euclide stesso non aveva esplicitato chiaramente.
Assiomi di Hilbert
L’esposizione che segue è una semplificazione degli assiomi del grande matematico tedesco; chi vuole studiare direttamente il testo originale può consultare http://www.gutenberg.org/files/17384/17384-pdf.pdf [ultima consultazione 31.03.2009].
Hilbert assume come enti primitivi della geometria piana il punto e la retta, come relazioni primitive l’appartenenza di un punto ad una retta, il giacere di un punto tra altri due punti, e la congruenza di segmenti.
ASSIOMI DI APPARTENENZA, legati dalla relazione “giacere su”:
- Dati due punti distinti, esiste una e una sola retta che contiene entrambi i punti.
- Ogni retta contiene almeno due punti. Esistono almeno tre punti che non giacciono su questa retta.
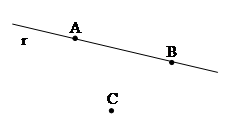
Figura 3. Due punti A e B giacciono sempre su un retta, questa retta è unica, esiste sempre almeno un terzo punto C che non giace sulla retta r.
Figura 3. Due punti A e B giacciono sempre su un retta, questa retta è unica, esiste sempre almeno un terzo punto C che non giace sulla retta r.
- Dati tre punti non allineati, esiste uno e un solo piano che contiene tutti e tre i punti. Ogni piano contiene almeno un punto.
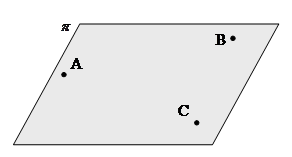
Figura 4. Per tre punti non allineati, A, B, C, passa un piano  , questo piano è unico.
, questo piano è unico.
- Se due punti di una retta giacciono su un piano, allora anche tutti gli altri punti della retta giacciono su questo piano.
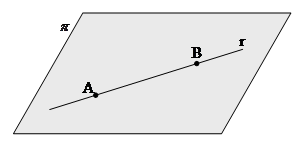
Figura 5. Se i punti A e B giacciono sul piano  .
.
- Se un punto giace su due piani distinti, allora esiste almeno un altro punto giacente su entrambi questi piani.
- Esistono almeno quattro punti che non giacciono sullo stesso piano.
ASSIOMI DI ORDINAMENTO, legati dalla relazione “stare fra”:
- Se un punto B giace fra i punti A e C, allora i punti A, B e C sono tre punti distinti sulla stessa retta, e B giace fra C ed A.
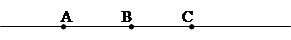
Figura 6. Se B sta tra A e C, allora sta anche tra C e A, e i tre punti sono allineati.
- Dati due punti A e C, esiste almeno un punto B, sulla retta AC, giacente fra di essi.
- Dati tre punti qualsiasi di una retta, uno e uno solo di essi giace fra gli altri due.
Gli ultimi assiomi ci permettono di dedurre il seguente
TEOREMA. Tra due punti di una retta esiste sempre una quantità illimitata di altri punti.
E di dare la seguente
DEFINIZIONE. Si chiama segmento AB l’insieme dei punti A e B e di tutti quelli che stanno tra A e B.
- Assioma di Pasch. Siano dati tre punti A, B e C non allineati, contenuti in un piano
 non contenente nessuno dei tre punti A, B, C: se d contiene un punto del segmento AB, allora contiene anche un punto di uno dei due segmenti AC e BC.
non contenente nessuno dei tre punti A, B, C: se d contiene un punto del segmento AB, allora contiene anche un punto di uno dei due segmenti AC e BC.

Figura 7. Assioma di Pash, se una retta d entra in un triangolo attraverso un lato AB deve uscire attraversando il lato CB o AC.
Gli assiomi di ordinamento ci permettono di dare anche la seguente
DEFINIZIONE. Presi quattro punti ABCO su una retta, in modo che B stia tra A e O e O stia tra A e C possiamo dire che A e B stanno dalla medesima parte rispetto a O, mentre A e C non stanno dalla medesima parte rispetto a O.
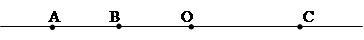
Figura 8. A e B stanno dalla medesima parte rispetto a O; A e C non stanno dalla medesima parte rispetto a O.
Assioma delle parallele
- Assioma di Euclide. Dati una retta r, un punto A non in r, ed un piano
 contenente A e non contenente nessun punto di r. Questa retta è detta parallela ad a passante per il punto P.
contenente A e non contenente nessun punto di r. Questa retta è detta parallela ad a passante per il punto P.
ASSIOMI DI CONGRUENZA, legati dalla relazione “essere congruente a”:
- Assioma del trasporto di un segmento. Se A, B sono due punti di una retta a e A' è un punto sulla stessa retta (o fissato su un’altra retta a'), si può sempre trovare un punto B' sulla retta a (o su a’), da una data parte rispetto ad A', tale che il segmento AB sia congruente al segmento A'B'.
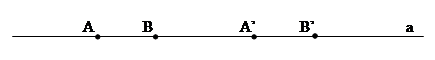
Figura 9. Assioma del trasporto di un segmento.
- La relazione di congruenza tra segmenti è transitiva, cioè se A′B′ e A′′B′′ sono congruenti ad AB, allora A′B′ è congruente a A′′B′′.
- Siano AB e BC segmenti su una retta r privi di punti comuni a parte B, e siano A′B′ e B′C′ segmenti su una retta r′ privi di punti comuni a parte B’. Se
 .
.

Figura 10. AB e A’B’ sono segmenti congruenti, anche BC e B’C’ sono segmenti congruenti, allora AC e A’C’ sono segmenti congruenti.
Prima di proseguire con gli altri assiomi premettiamo la seguente
DEFINIZIONE. Chiamiamo semiretta la parte di retta costituita da un punto di essa, detto origine della semiretta, e da tutti i punti che stanno dalla stessa parte rispetto all’origine.

Figura 11. Semiretta
DEFINIZIONE. Si dice angolo ciascuna delle due parti in cui un piano è diviso da due semirette aventi l’origine in comune; le semirette si dicono lati dell’angolo; l’origine comune alle due semirette si dice vertice dell’angolo.
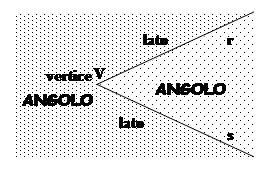
Figura 12. Le semirette r e s, aventi l’origine V comune individuano due regioni del piano dette angolo.
L’angolo individuato da tre punti ABC è l’angolo formato dalla semiretta con origine B e passante per A e dalla semiretta con origine B e passante per C. Questo angolo si indica con il simbolo 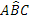 . Graficamente si usa indicare un angolo con un archetto.
. Graficamente si usa indicare un angolo con un archetto.

Figura 13. L’angolo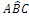 .
.
- Dati un angolo
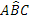 .
.

Figura 14. Assioma XVI, dato 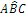 ed aventi un lato su una semiretta prefissata.
ed aventi un lato su una semiretta prefissata.
- La relazione di congruenza tra angoli è transitiva, cioè se
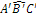 .
. - Primo criterio di congruenza dei triangoli. Se per due triangoli ABC e A′B′C′ si ha che
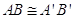 , allora tutto il triangolo ABC è congruente al triangolo A′B′C′.
, allora tutto il triangolo ABC è congruente al triangolo A′B′C′.

Figura 15. Primo criterio di congruenza dei triangoli
Assiomi di continuità
- Assioma di Archimede. Sulla retta che unisce due punti qualsiasi A e B si prende un punto A1, si prendono poi i punti A2, A3, A4, … in modo che A1 sta tra A e A2, A2 sta tra A1 e A3, A3 tra A2 e A4 ecc. e che
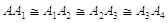 ecc. Allora tra tutti questi punti esiste sempre un certo punto An tale che B sta tra A e An.
ecc. Allora tra tutti questi punti esiste sempre un certo punto An tale che B sta tra A e An.
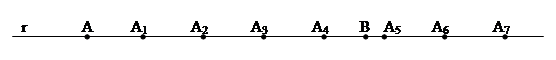
Figura 16. Dati i punti A e B sulla retta r si può sempre costruire la serie di segmenti congruenti 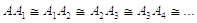 in modo da superare il punto B.
in modo da superare il punto B.
Assioma di completezza
- Ad un sistema di punti, linee rette e piani è impossibile aggiungere altri elementi in modo tale che il sistema, così generalizzato, formi una nuova geometria obbediente a tutti i cinque gruppi di assiomi. In altre parole gli elementi della geometria formano un sistema che non è suscettibile di estensione, nel caso in cui si considerino validi i cinque gruppi di assiomi.
19 Gli enti primitivi della geometria sono quelli
- Che occorre definire
- Che occorre dimostrare
- Che non si definiscono
- Che si conoscono già per averli studiati prima
20 Gli assiomi sono
- Proposizioni note che si preferisce non dimostrare per non appesantire lo studio
- Proposizioni che è necessario dimostrare
- Proposizioni che si assumono vere senza dimostrazione
- Proposizioni che non si definiscono
- Proposizioni che non si dimostrano perché la loro dimostrazione è molto semplice
21 Quali delle seguenti affermazioni sono vere?
- Due punti sono sempre allineati V F
- Tre punti sono sempre allineati V F
- Tre punti sono sempre complanari V F
- Tre punti allineati individuano un unico piano V F
- Una retta e un punto esterno ad essa individuano un piano V F
22 Distingui nelle seguenti frasi le definizioni dalle proposizioni o proprietà
- La Terra ruota su se stessa in un giorno.
- Il solstizio è il momento in cui il Sole raggiunge, nel suo moto apparente lungo l'eclittica, il punto di declinazione massima o minima.
- La cellula è l'unità fondamentale di tutti gli organismi viventi.
- I virus sono responsabili di alcune malattie.
- I numeri che hanno per ultima cifra 0 sono numeri pari.
- Un numero si dice pari se è divisibile per 2.
23 Su una retta si segnano quattro punti ABCD, quanti segmenti restano individuati?
24 Date tre semirette a, b, c aventi la stessa origine O, quanti angoli restano individuati?
25 Unisci in tutti i modi possibili mediante rette tre punti non allineati e posti sullo stesso piano.
26 Unisci in tutti i modi possibili mediante rette quattro punti, a tre a tre non allineati, di uno stesso piano.
27 Quattro rette a due a due incidenti quanti punti di intersezioni individuano complessivamente?
 English corner
English corner
Alcuni degli assiomi di Hilbert nella versione integrale in inglese
GROUP I: AXIOMS OF CONNECTION
The axioms of this group establish a connection between the concepts indicated above; namely, points, straight lines, and planes. These axioms are as follows:
I, 1. Two distinct points A and B always completely determine a straight line a.
I, 2. Any two distinct points of a straight line completely determine that line; that is, if AB = a and AC = a, where B 6= C, then is also BC = a.
I, 3. Three points A, B, C not situated in the same straight line always completely determine a plane α.
I, 4. Any three points A, B, C of a plane α, which do not lie in the same straight line, completely determine that plane.
I, 5. If two points A, B of a straight line a lie in a plane α then every point of a lies in α.
I, 6. If two planes α e β, have a point A in common, then they have at least a second point B in common.
I, 7. Upon every straight line there exist at least two points, in every plane at least three points not lying in the same straight line, and in space there exist at least four points not lying in a plane.
3. PRIME DEFINIZIONI: SEGMENTI e ANGOLI
►1. Semirette e segmenti
Nel paragrafo precedente abbiamo già introdotto alcune definizioni di base, necessarie per enunciare tutti i postulati della geometria secondo l’assiomatizzazione di Hilbert. In questo paragrafo costruiamo le prime definizioni. Per comodità del lettore riportiamo anche quelle già date.
Partiamo dalla nozione generica di figura.
DEFINIZIONE. Si chiama figura un qualsiasi insieme, non vuoto, di punti.
Questa definizione fa riferimento soltanto all’ente primitivo geometrico di punto.
Lo spazio non è considerato un ente primitivo, in quanto può essere ottenuto dalla seguente definizione.
DEFINIZIONE. Si chiama spazio l’insieme di tutti i punti.
Risulta pertanto che una figura è un qualsiasi sottoinsieme dello spazio.
In base agli assiomi di ordinamento un qualunque punto P su una retta divide la retta in due parti, una è costituita dai punti che ‘seguono’ P, l’altra è costituita dai punti che ‘precedono’ P.
DEFINIZIONE. Si chiama semiretta la parte di retta costituita da un punto di essa, detto origine della semiretta, e da tutti i punti che stanno dalla stessa parte rispetto all’origine.

Figura 17. Semiretta di origine O
Solitamente, la semiretta si indica con una lettera latina minuscola.
Prendendo due qualsiasi rette dello spazio esse si possono trovare in diverse posizioni reciproche, cioè una rispetto all’altra.
DEFINIZIONE.
Due rette si dicono complanari se appartengono a uno stesso piano; se non appartengono a uno stesso piano si dicono sghembe.
Due rette complanari si dicono incidenti se hanno uno, e uno solo, punto in comune.
Due rette complanari che non hanno nessun punto in comune si dicono parallele.
 Se due rette hanno almeno due punti in comune sono coincidenti.
Se due rette hanno almeno due punti in comune sono coincidenti.
Figura 18. Rette coincidenti (r ed s), incidenti (u e v), parallele (m e n).
Per indicare che le rette r e s sono parallele si usa il simbolo r//s.
Fai attenzione al fatto che due rette non parallele possono appartenere a piani diversi, in questo caso non avranno punti in comune, sono cioè sghembe. Viceversa se due rette hanno un punto in comune allora sono sicuramente complanari. Inoltre, se hanno più di un punto in comune le rette coincidono, in questo caso ci sono infiniti piani che le contengono.
DEFINIZIONE. L’insieme di tutte le rette di un piano che passano per uno stesso punto è detto fascio proprio di rette, il punto in comune a tutte le rette si dice centro del fascio.

Figura 19. Fascio proprio di rette di centro P.
Prendendo due punti su una retta, A e B, la retta resta divisa in tre parti: la semiretta di origine A che non contiene B, la parte costituita dai punti compresi tra A e B e la semiretta di origine B che non contiene A.
DEFINIZIONE. Si chiama segmento AB l’insieme dei punti A e B e di tutti quelli che stanno tra A e B. I punti A e B si dicono estremi del segmento.

Figura 20. I punti A e B formano le due semirette, r e s, e il segmento AB.
Un segmento viene indicato con le due lettere maiuscole dei suoi estremi.
Due segmenti nel piano possono trovarsi in diverse posizioni reciproche. Alcune di esse hanno un interesse per la geometria.
 DEFINIZIONE. Due segmenti si dicono consecutivi se hanno in comune soltanto un estremo.
DEFINIZIONE. Due segmenti si dicono consecutivi se hanno in comune soltanto un estremo.
Figura 21. I segmenti AB e BC sono consecutivi perché hanno in comune solo il punto B che è un estremo di entrambi; DE e FG non sono consecutivi perché hanno in comune solo il punto F ma esso non è estremo del segmento DE; HI e LM non sono consecutivi perché non hanno nessun punto in comune.
DEFINIZIONE. Due segmenti si dicono adiacenti se sono consecutivi ed appartengono alla stessa retta.
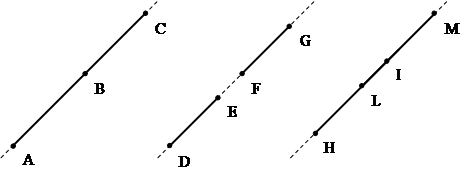
Figura 22. I segmenti AB e BC sono adiacenti perché hanno in comune solo l’estremo B e giacciono sulla stessa retta; i segmenti DE e FG non sono adiacenti; i segmenti HI e LM non sono adiacenti.
28 Disegna una retta a e una retta b che si incontrano in un punto X, disegna anche una retta c che incontra la a in Y e la b in Z. Elenca tutte le semirette e tutti i segmenti che si vengono a formare.
29 Disegna due rette a e b parallele tra di loro; disegna poi la retta c che interseca la a in A e la b in B; disegna poi la retta d che interseca a in A e b in C. Quali segmenti si vengono a formare?
30 Rappresenta graficamente ciascuna delle seguenti situazioni:
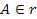
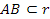 ?
?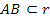 ?
? ,
, 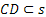
31 Attribuisci il nome corretto a ciascuna coppia di segmenti: adiacenti, incidenti, disgiunti, consecutivi:
►2. Semipiani e angoli
DEFINIZIONE. Si dice semipiano di origine la retta r la figura formata dalla retta r e da una delle due parti in cui essa divide il piano.
In un piano p, una qualsiasi retta r Ì p dà origine a due semipiani distinti, che si dicono semipiani opposti.
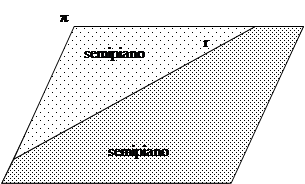
Figura 23. La retta r divide il piano π in due semipiani opposti.
DEFINIZIONE. Una figura si dice convessa se, considerati due suoi qualsiasi punti, il segmento che li unisce è contenuto nella figura. Si dice concava se esistono almeno due punti per i quali il segmento che li unisce non è interamente contenuto nella figura.
Figura 24. La figura F è convessa, per qualsiasi coppia di punti interni a F il segmento che li unisce è interamente nella figura; la figura G è concava perché unendo i punti P e Q si ha un segmento che cade in parte esternamente alla figura.
Figura 24. La figura F è convessa, per qualsiasi coppia di punti interni a F il segmento che li unisce è interamente nella figura; la figura G è concava perché unendo i punti P e Q si ha un segmento che cade in parte esternamente alla figura.
DEFINIZIONE. Si dice angolo ciascuna delle due parti in cui un piano è diviso da due semirette aventi l’origine in comune; le semirette si dicono lati dell’angolo; l’origine comune alle due semirette si dice vertice dell’angolo.
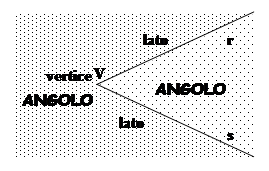
Figura 25. Le semirette r e s, aventi l’origine V comune individuano due regioni del piano dette angolo.
DEFINIZIONE
Un angolo si dice angolo piatto se i suoi lati sono uno il prolungamento dell’altro.
Un angolo si dice angolo nullo se è costituito solo da due semirette sovrapposte.
Si dice angolo giro l’angolo che ha per lati due semirette sovrapposte e che contiene tutti i punti del piano.
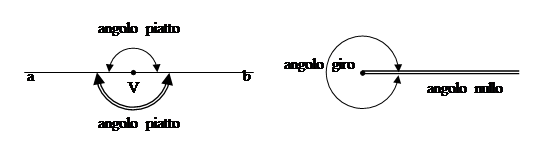
Figura 25. L’angolo  a sinistra è piatto, gli angoli a destra sono rispettivamente un angolo giro e un angolo nullo.
a sinistra è piatto, gli angoli a destra sono rispettivamente un angolo giro e un angolo nullo.
DEFINIZIONE. Un angolo, i cui lati non appartengono alla stessa retta, si dice concavo se contiene i prolungamenti dei lati, se non li contiene si dice convesso.
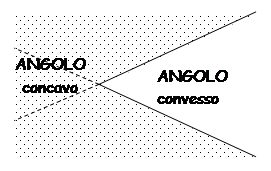
Figura 26. L’angolo concavo è quello punteggiato in quanto contiene i prolungamenti dei lati.
Quando si disegna un angolo è utile, oltre a disegnare le semirette e l’origine, indicare con un archetto quale dei due angoli si intende considerare.

Figura 27. Per indicare che l’angolo da considerare è quello convesso e non quello concavo si è usato un archetto in prossimità del vertice O.
Per indicare gli angoli si usano diverse convenzioni:
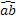 se si conoscono i nomi delle semirette che ne costituiscono i lati;
se si conoscono i nomi delle semirette che ne costituiscono i lati;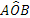 se si conoscono i nomi del vertice e di due punti sui lati;
se si conoscono i nomi del vertice e di due punti sui lati; una lettera greca per indicare direttamente l’angolo.
una lettera greca per indicare direttamente l’angolo.
I primi due modi di indicare l’angolo non individuano con chiarezza di quale dei due angoli si tratta. Solitamente si intende l’angolo convesso, quando si vuole indicare l’angolo concavo bisogna dirlo esplicitamente.
Anche per gli angoli si danno le definizioni di angoli consecutivi e angoli adiacenti, in parte simili a quelle date per i segmenti.
DEFINIZIONE. Due angoli si dicono angoli consecutivi se hanno il vertice e un lato comune e giacciono da parte opposta rispetto al lato comune.
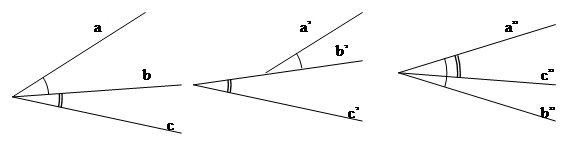
Figura 28. Nella figura gli angoli  non sono consecutivi perché non giacciono da parti opposte rispetto al lato in comune a”.
non sono consecutivi perché non giacciono da parti opposte rispetto al lato in comune a”.
DEFINIZIONE. Due angoli si dicono angoli adiacenti se sono consecutivi e se i lati non comuni giacciono sulla stessa retta.
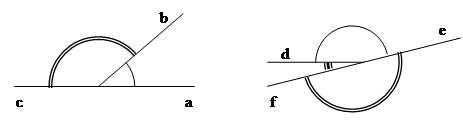
Figura 29. I due angoli 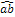 sono adiacenti in quanto f è il prolungamento di e.
sono adiacenti in quanto f è il prolungamento di e.
DEFINIZIONE. Due angoli convessi si dicono angoli opposti al vertice se i lati del primo sono i prolungamenti dei lati dell’altro.

Figura 30. Gli angoli formati dalle semirette a sinistra sono opposti al vertice; gli angoli formati dalle semirette a destra non lo sono.
32 Per ciascuna figura scrivi di che angolo si tratta relativamente agli angoli colorati in grigio, scegliendo i termini tra: angolo concavo, angoli adiacenti, angoli consecutivi, angoli opposti al vertice.
33 Rappresenta graficamente ciascuna delle seguenti situazioni:
a)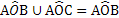
b) 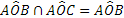
c) 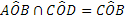
 34 Nella figura a fianco indica
34 Nella figura a fianco indica
- Una coppia di segmenti consecutivi … …
- Una coppia di segmenti adiacenti … …
- Una coppia di rette incidenti … …
- Una coppia di rette parallele … …
- Una coppia di angoli consecutivi … … … …
- Una coppia di angoli adiacenti … … … …
- Una coppia di angoli opposti al vertice … … … ….
- Un angolo concavo … …
- Un angolo convesso … …
►3. Posizioni reciproche di semipiani
Siano p’ e p” due semipiani di un piano a, aventi per origine rispettivamente le rette r’ e r”. La loro unione e la loro intersezione danno luogo a figure diverse tra loro a seconda dei vari casi possibili.
1° caso r’ ed r” sono incidenti in un punto O. Allora l’intersezione dei due semipiani (p’Çp”) è un angolo convesso di vertice O, mentre la loro unione (p’Èp”) è un angolo concavo di vertice O.
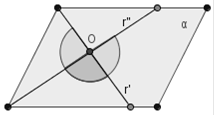
Figura 31. Le due semirette r’ e r”, origini dei semipiani p’ e p” sono incidenti; in questo caso l’unione dei due semipiani è l’angolo concavo di colore grigio chiaro, la loro intersezione è l’angolo convesso di colore grigio scuro.
2° caso r’ ed r” sono coincidenti, p’ e p” anch’essi coincidenti, cioè perfettamente sovrapposti. In questo caso particolare l’intersezione e l’unione dei due semipiani coincidono con gli semipiani (p’Çp” = p’Èp” = p’ = p”). Osserva che un semipiano è anche un angolo piatto.
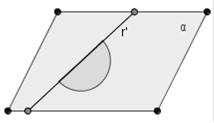
Figura 32. I due semipiani hanno la stessa retta di origine e sono anche coincidenti: la loro unione e la loro intersezione coincide con i semipiani stessi e formano lo stesso angolo piatto.
3° caso r’ ed r” sono coincidenti, con p’ e p” distinti, e dunque opposti. In tal caso particolare l’intersezione dei due semipiani coincide con la retta origine in comune (p’Çp” = r’ = r”) e l’unione di essi coincide con l’intero piano (p’Èp” = a). Notiamo che un piano è anche un angolo giro.
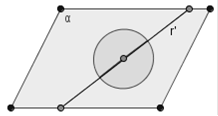
Figura 33. I due semipiani hanno la stessa retta di origine e si trovano da parti opposte: la loro unione coincide con l’intero piano (angolo giro).
4° caso r’ ed r” sono parallele e distinte, cioè non hanno punti in comune, ed inoltre p’ non contiene r” e p” non contiene r’. In tal caso i due semipiani non hanno punti in comune, cioè la loro intersezione è vuota (p’Çp” = Æ) mentre la loro unione è una parte (“sconnessa”) del piano a costituita da tutti i punti di a tranne la parte (convessa) delimitata dalle due semirette r’ ed r”.
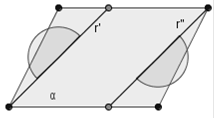
Figura 34. Le rette di origine sono parallele e distinte, i semipiani non hanno punti in comune, la loro unione è costituita dall’unione dei due angoli piatti indicati con un archetto grigio.
5° caso r’ ed r” sono parallele e distinte, cioè non hanno punti in comune, ed inoltre p’ contiene r” e p” non contiene r’ [o viceversa]. In tal caso l’intersezione dei due semipiani coincide con uno dei due semipiani e la loro unione coincide con l’altro semipiano (p’Çp” = p” e p’Èp” = p’) [o, rispettivamente, p’Çp” = p’ e p’Èp” = p”].
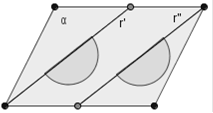
Figura 35. Le rette di origine sono parallele e distinte, uno dei due semipiani contiene l’altro; la loro unione è l’angolo piatto con lati sulla retta r’, la loro intersezione è l’angolo piatto con lati sulla retta r”
6° caso r’ ed r” sono parallele e distinte, cioè non hanno punti in comune, ed inoltre p’ contiene r” e p” contiene r’. In tal caso l’unione dei due semipiani è l’intero piano (p’Èp” = a), mentre l’intersezione di essi è la parte (convessa) di a delimitata dalle due semirette r’ ed r”. Tale intersezione (p’Çp”) prende il nome di striscia di piano delimitata dalle rette r’ ed r” che sono dette lati della striscia.
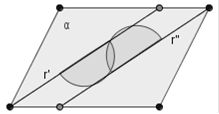
Figura 36. Le rette di origine sono parallele e distinte, ognuno dei due semipiani contiene l’altra retta, la loro unione è formata da tutto il piano, la loro intersezione forma una striscia di piano, delimitata dalle rette r’ e r”, dette lati della striscia.
►4. Altri esercizi
35 Vero o falso?
- Due punti distinti del piano individuano sempre un segmento V F
- Due rette distinte del piano hanno al più un punto in comune V F
- Tre punti distinti del piano individuano almeno tre rette V F
- Due semirette distinte del piano che hanno la stessa origine sono opposte V F
- Alcuni segmenti consecutivi non sono adiacenti V F
- Due angoli che hanno il vertice in comune sono consecutivi V F
- Per un punto del piano passano solo due rette V F
- Due segmenti posti sulla stessa retta sono adiacenti V F
36 Due segmenti si dicono adiacenti se:
[A] appartengono alla stessa retta
[B] sono consecutivi ma non appartengono alla stessa retta
[C] non sono consecutivi e appartengono alla stessa retta
[D] sono consecutivi e appartengono alla stessa retta
[E] appartengono alla stessa retta e hanno gli estremi coincidenti
37 Un angolo è convesso se:
[A] è adiacente ad un altro angolo [B] i suoi lati sono rette incidenti
[C] contiene il prolungamento dei suoi lati [D] è consecutivo ad un altro angolo
[E] non contiene il prolungamento dei suoi lati
38 Due angoli si dicono opposti al vertice se:
[A] sono sullo stesso piano [B] sono uno concavo e uno convesso
[C] se hanno il vertice in comune [D] se i lati dell'uno sono contenuti nell'altro
[E] se i lati dell'uno sono il prolungamento dei lati dell'altro
39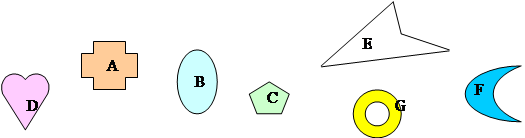 Sono convesse le figure
Sono convesse le figure
[A] A, B, C, G [B] D, C, B, F [C] B, C, D [D] B, C [E] D, E, F, G
40 Scrivi per esteso in italiano quanto è indicato in simboli e rappresenta con un disegno tutti i casi possibili:  .
.
41 Descrivi la costruzione della seguente figura, dove le rette c e d sono parallele
42 Se P è centro di un fascio di rette e A è un punto dello stesso piano, è vero che “Nel fascio di centro P esiste una retta passante per A”?
43 Motiva la verità o la falsità della proposizione: "Tutte le rette incidenti formano 2 coppie di angoli opposti al vertice".
4. CONFRONTO E OPERAZIONI FRA SEGMENTI E ANGOLI
►1. Premessa intuitiva
Nel linguaggio comune usiamo la parola ‘uguale’ con un significato generico, spesso per indicare due oggetti che si assomigliano: due macchine uguali, due orologi uguali… In aritmetica e in algebra usiamo la parola ‘uguale’ per indicare oggetti matematici perfettamente uguali. Per esempio, 2=2, ogni numero infatti è uguale solo a se stesso. Scriviamo anche 3+2=5, per dire che il numero che si ottiene dalla somma di 3 e 2 è proprio il numero 5. Nei polinomi si enuncia il principio di identità dei polinomi, in base al quale due polinomi sono uguali se si possono scrivere formalmente allo stesso modo.
In geometria, usiamo il termine ‘uguale’ per indicare due figure coincidenti nella forma e nella posizione. In altre parole due figure sono uguali solo se sono esattamente la stessa figura. Tuttavia, in geometria siamo interessati a studiare soprattutto figure che senza essere del tutto identiche hanno delle caratteristiche in comune. Vediamo prima degli esempi intuitivi e successivamente tratteremo lo stesso tema ma in modo formalmente corretto.
Le figure che seguono hanno la stessa forma ma una è più grande dell’altra, la seconda infatti è stata ottenuta dalla prima raddoppiando i lati: in geometria si dicono simili.
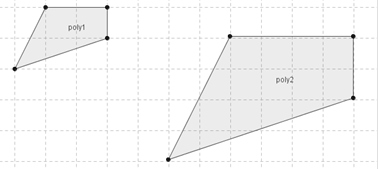
Figura 37. Le figure poly1 e poly2 hanno la stessa forma ma una è più grande dell’altra.
Queste due altre figure non hanno la stessa forma, non si somigliano affatto, però le loro superfici hanno la stessa estensione, in quanto sono costituite dallo stesso numero di quadratini: in geometria si dicono equivalenti.
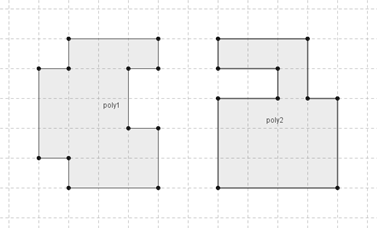
Figura 38. Le figure poly1 e poly2 non hanno la stessa forma ma hanno la stessa estensione.
Le figure che seguono hanno la stessa forma e le stesse dimensioni ma sono in posizioni differenti, è però possibile spostare una sull’altra senza deformarle e farle coincidere. Usualmente le chiamiamo figure uguali, in geometria si dicono congruenti.
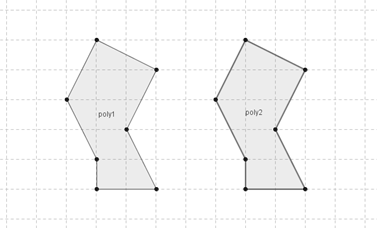
Figura 39. Le figure poly1 e poly2 hanno la stessa forma e le stesse dimensioni.
Le due figure che seguono hanno la stessa forma e le stesse dimensioni, per rendersene conto occorre ruotare per esempio la seconda figura in senso antiorario (si può ruotare anche in senso orario ma di un angolo maggiore) e poi trascinarla sulla prima per sovrapporla. Anche queste figure sono dette uguali nel linguaggio comune, in geometria si dicono congruenti.

Figura 40. Le figure poly5 e poly6 hanno stessa forma e stesse dimensioni, per rendersene conto è sufficiente ruotare poly6 in senso antiorario, finché il lato verticale diventa orizzontale, e trascinarla per sovrapporla alla prima.
Le due figure che seguono hanno stessa forma e stesse dimensioni, tuttavia non si riesce a trasportare l’una sull’altra muovendole nel piano, né trascinandole, né ruotandole, occorre ribaltarne una facendola uscire dal piano; le due figure sono una l’immagine speculare dell’altra. In geometria, se due figure piane sono tali che, spostandone una senza deformarla, possono essere poste in maniera tale che una sia l’immagine speculare dell’altra, diciamo che sono inversamente congruenti.
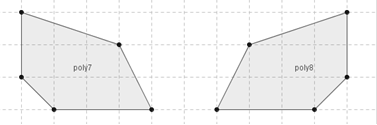
Figura 41. Le figure poly7 e poly8 sono sovrapponibili ma occorre ribaltare una sull’altra.
Osserviamo i due segmenti AB e CD rappresentati nella figura che segue. I due segmenti sono sovrapponibili, e quindi congruenti, infatti basta fare scorrere il segmento CD lungo la retta fino a far coincidere C con A, il punto D coinciderà con B. Tuttavia, se portiamo D a coincidere con A dobbiamo poi ribaltare il segmento CD in modo che A coincida con D e B coincida con C.

Figura 42. I segmenti AB e CD sono direttamente congruenti in quanto si può far coincidere A con C e B con D semplicemente facendo scorrere lungo la retta un segmento sull’altro. Se invece vogliamo far coincidere A con D e B con C occorre ribaltare, uscendo fuori dalla retta, uno dei due segmenti.
Osserva che per ribaltare una figura occorre una dimensione in più, precisamente se si tratta di due figure piane occorre avere la terza dimensione per ribaltare una figura piana, se siamo su una retta occorre la seconda dimensione per ribaltare un segmento.
Per renderci conto di quanto accade con le figure solide, possiamo pensare ai palmi delle nostre mani che con buona approssimazione si possono considerare inversamente congruenti: esse possono essere giunte, ma non sovrapposte nel senso in cui si parla a proposito delle figure piane. Infatti non è possibile vedere le proprie mani, entrambe dal dorso o entrambe dal palmo, con le dita rivolte verso l’alto, in modo che in ciascuna di esse il pollice sia a sinistra oppure a destra.
►2. La congruenza
Secondo il punto di vista del matematico tedesco Felix Klein (1848-1925), la geometria è lo studio delle proprietà delle figure che sono invarianti rispetto a certe trasformazioni. Nello studio della geometria euclidea, quella che tratteremo in questo Tema, ci occupiamo delle proprietà delle figure geometriche invarianti rispetto ai movimenti rigidi, cioè rispetto a quei movimenti che conservano forma e dimensioni delle figure. Queste trasformazioni vengono anche dette isometrie (si intuisce dalla radice etimologica che si parla di stessa misura): significa che viene stabilita una corrispondenza biunivoca tra i punti di due figure congruenti in modo da “mantenere” le distanze.
DEFINIZIONE. Diciamo che due figure F e G sono congruenti quando esiste un movimento rigido che le sovrappone perfettamente. In simboli 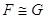 .
.
Nella Premessa a questo paragrafo abbiamo dato un’idea intuitiva e sperimentale del concetto di congruenza. Ma per esplicitarlo matematicamente dobbiamo utilizzare gli assiomi di congruenza di Hilbert che abbiamo enunciato nel Capitolo 1 Paragrafo 2. Ne riportiamo alcuni per comodità del lettore.
Assiomi di congruenza
- Assioma del trasporto di un segmento. Se A, B sono due punti di una retta a e A' è un punto sulla stessa retta o su un’altra retta a', si può sempre trovare un punto B' sulla retta a o su a’, da una data parte rispetto ad A', tale che il segmento AB sia congruente al segmento A'B'.
Questo assioma afferma che, fissato un punto A’ su una retta a’, è sempre possibile trasportare un qualunque segmento AB in modo che l’estremo A coincida con A’ e il segmento stia sulla retta a’.
- La relazione di congruenza tra segmenti è transitiva, cioè se A′B′ e A′′B′′ sono congruenti ad AB, allora A′B′ è congruente a A′′B′′.
La relazione di congruenza tra segmenti è allora un relazione di equivalenza, in quanto gode delle proprietà:
- riflessiva: ogni segmento è congruente a se stesso;
- simmetrica: se AB è congruente a A’B’ allora anche A’B’ è congruente ad AB;
- transitiva: se AB è congruente ad A’B’ e A’B’ è congruente ad A”B”, allora AB è congruente ad A”B”.
DEFINIZIONE. Si dice lunghezza di un segmento la classe di equivalenza dei segmenti congruenti tra di loro, cioè l’insieme di tutti i segmenti che sono congruenti tra di loro.
- Assioma del trasporto di un angolo. Dati un angolo
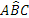 .
.
Questo assioma ci garantisce che è sempre possibile trasportare un angolo 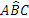 su una qualsiasi semiretta s, facendo coincidere il vertice dell’angolo con l’origine della semiretta e un lato dell’angolo con la semiretta s.
su una qualsiasi semiretta s, facendo coincidere il vertice dell’angolo con l’origine della semiretta e un lato dell’angolo con la semiretta s.
- La relazione di congruenza tra angoli è transitiva, cioè se
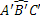 .
.
Quindi anche la relazione di congruenza tra gli angoli è una relazione di equivalenza, gode cioè delle proprietà riflessiva, simmetrica, transitiva.
DEFINIZIONE. Si dice ampiezza di un angolo la classe di equivalenza degli angoli congruenti tra di loro, cioè l’insieme di tutti gli angoli che sono congruenti tra di loro.
Aggiungiamo che:
- Tutte le rette sono fra loro congruenti;
- Tutte le semirette sono fra loro congruenti;
- Tutti i piani sono fra loro congruenti;
- La relazione di congruenza tra angoli è transitiva, cioè se
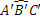 .
.
Quindi anche la relazione di congruenza tra gli angoli è una relazione di equivalenza, gode cioè delle proprietà riflessiva, simmetrica, transitiva.
DEFINIZIONE. Si dice ampiezza di un angolo la classe di equivalenza degli angoli congruenti tra di loro, cioè l’insieme di tutti gli angoli che sono congruenti tra di loro.
Aggiungiamo che:
- Tutte le rette sono fra loro congruenti;
- Tutte le semirette sono fra loro congruenti;
- Tutti i piani sono fra loro congruenti;
►3. Confronto di segmenti e angoli
Per confrontare l’altezza di due persone e vedere chi è più alto, facciamo mettere affiancate le due persone in modo che i piedi stiano allo stesso livello, dopo di che confrontiamo l’estremità della testa: è più alto chi ha l’estremità della testa più in alto. Un procedimento analogo si fa per confrontare due segmenti.
Per confrontare due segmenti AB e CD, facciamo in modo che con un movimento rigido gli estremi A e C coincidano, con una rotazione intorno al punto A facciamo in modo che coincidano anche le rette AB e CD e che gli estremi B e D stiano dalla stessa parte rispetto ad A e C.

Figura 43. Confronto di due segmenti
A questo punto possono verificarsi tre situazioni possibili:
- B cade dopo l’estremo D, allora diciamo che AB è maggiore di CD, scriviamo AB>CD;
- B cade esattamente su D, allora i due segmenti sono congruenti;
- B cade tra C e D, allora diciamo che AB è minore di CD, scriviamo AB<CD.
Per confrontare due angoli 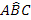 , portiamo con un movimento rigido il vertice B sul vertice E, con una rotazione portiamo a coincidere la semiretta BA con la semiretta ED, in modo che le altre due semirette, BC e EF, stiano dalla stessa parte rispetto a BA.
, portiamo con un movimento rigido il vertice B sul vertice E, con una rotazione portiamo a coincidere la semiretta BA con la semiretta ED, in modo che le altre due semirette, BC e EF, stiano dalla stessa parte rispetto a BA.

Figura 44. Confronti di due angoli
A questo punto si possono avere tre situazioni distinte:
- Il lato EF cade internamente all’angolo
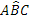 ;
; - Il lato EF cade esattamente su BC, i due angoli sono congruenti;
- Il lato EF cade esternamente all’angolo
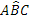 .
.
►4. Operazioni con i segmenti
Somma di due segmenti. La somma di due segmenti AB e CD è il segmento AD che si ottiene trasportando con un movimento rigido il segmento CD in modo che AB e CD siano adiacenti, con l’estremo B coincidente con C. Scriviamo ab + cd = AD , usando l’usuale simbolo di addizione.
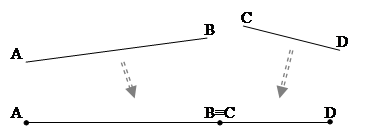
Figura 45. Il segmento AD è la somma dei segmenti AB e CD.
Differenza di due segmenti. La differenza di due segmenti AB e CD, con AB>CD, è il segmento DB che si ottiene sovrapponendo AB e CD facendo coincidere l’estremo A con l’estremo C. Scriviamo AB – CD = DB
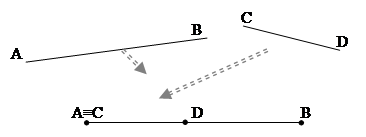
Figura 46. Il segmento DB è la differenza tra i segmenti AB e CD.
Multiplo di un segmento. Il multiplo secondo m, numero naturale diverso da zero, di un segmento AB è il segmento AC che si ottiene sommando m volte il segmento AB a se stesso.

Figura 47. In figura 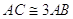
Se m=0, il multiplo secondo m di qualsiasi segmento AB è il segmento nullo, ove per segmento nullo intendiamo un qualsiasi segmento in cui gli estremi coincidono, cioè il segmento ridotto al solo punto A.
Sottomultiplo di un segmento. Il sottomultiplo secondo n, numero naturale diverso da 0, di un segmento AB è un segmento AC tale che 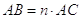 .
.
In generale il segmento 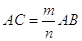 si ottiene dividendo AB in n parti uguali ottenendo il segmento AD e poi sommando m segmenti congruenti ad AD.
si ottiene dividendo AB in n parti uguali ottenendo il segmento AD e poi sommando m segmenti congruenti ad AD.
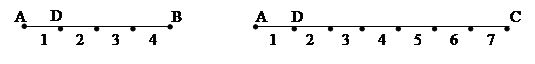
Figura 48. Il segmento AC è congruente a 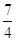 , infatti AB è stato diviso in 4 parti uguali e AC è costituito da 7 di queste parti.
, infatti AB è stato diviso in 4 parti uguali e AC è costituito da 7 di queste parti.
Punto medio. Dato un segmento AB esiste uno e uno solo punto M che lo divide in due parti congruenti tra di loro, questo punto si dice punto medio del segmento.
Figura 49. M è il punto medio del segmento AB in quanto 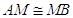 .
.
DEFINIZIONE. Si chiama punto medio di un segmento il punto interno al segmento che lo divide in due parti congruenti.
Proprietà
- somme di segmenti a due a due congruenti sono congruenti;
- differenze di segmenti a due a due congruenti sono congruenti.
44 Su una semiretta di origine A segna il segmento AB, il segmento BC=3AB e il segmento 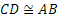 , i punti sono consecutivi secondo l’ordine alfabetico. Secondo quale numero frazionario AD e multiplo di BC?
, i punti sono consecutivi secondo l’ordine alfabetico. Secondo quale numero frazionario AD e multiplo di BC?
45 Su una semiretta di origine O si hanno i segmenti OA e OB con OB>OA. Se M è il punto medio di OA e N è il punto medio di OB, quale delle due seguenti relazioni è vera?
[A] 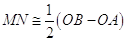
46 Su una semiretta di origine O si prendono i punti ABC con OC>OB>OA. Sia M il punto medio di OA e N il punto medio di BC. Quale delle seguenti relazioni è vera?
[A] 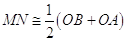
47 Su una retta i punti A, B, C, D si susseguono secondo l’ordine alfabetico. Se AB è congruente a CD i punti medi di BC e AD coincidono? Sai spiegare perché?
5. Operazioni con gli angoli
Somma di angoli. La somma di due angoli consecutivi 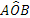 , la somma di questi due angoli consecutivi si dice anche somma dei due angoli.
, la somma di questi due angoli consecutivi si dice anche somma dei due angoli.

Figura 50. Somma di due angoli
Differenza di angoli. Si dice differenza di due angoli, di cui il primo è maggiore o congruente al secondo, l’angolo che addizionato al secondo dà per somma il primo.
Figura 51. Angolo differenza  .
.
Se i due angoli sono congruenti la loro differenza è l’angolo nullo.
Multiplo di un angolo. Dato un angolo  è l’angolo nullo.
è l’angolo nullo.

Figura 52. L’angolo 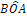
Sottomultiplo di un angolo. Il sottomultiplo secondo n, naturale non nullo, di un angolo 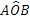 .
.
In generale un angolo 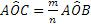 .
.
DEFINIZIONE. Si dice bisettrice di un angolo la semiretta che ha origine nel vertice dell’angolo e divide l’angolo in due angoli congruenti.

Figura 53. la semiretta c di origine O è la bisettrice dell’angolo  .
.
►6. Angoli particolari
Possiamo ora dare dei nomi ai seguenti angoli particolari.
- Si dice angolo retto la metà di un angolo piatto.

Figura 54. L’angolo retto è la metà di un angolo piatto: 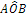 sono retti.
sono retti.
- Due angoli si dicono angoli complementari se la loro somma è un angolo retto.

Figura 55. Gli angoli 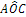 .
.
- Due angoli si dicono angoli supplementari se la loro somma è un angolo piatto.

Figura 56. Gli angoli 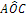 .
.
- Due angoli si dicono angoli esplementari se la loro somma è un angolo giro.

Figura 57. Gli angoli 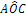 sono esplementari perché la loro somma è l’angolo giro.
sono esplementari perché la loro somma è l’angolo giro.
- Un angolo si dice angolo acuto se è minore di un angolo retto.
Figura 57. Gli angoli 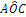 sono esplementari perché la loro somma è l’angolo giro.
sono esplementari perché la loro somma è l’angolo giro.
- Un angolo si dice angolo acuto se è minore di un angolo retto.
- Un angolo convesso si dice angolo ottuso se è maggiore di un angolo retto.

Figura 58. L’angolo acuto è minore di un angolo retto, l’angolo ottuso è maggiore di un angolo retto.
TEOREMA. Angoli opposti al vertice sono congruenti.
 Con riferimento alla figura a lato
Con riferimento alla figura a lato
Ipotesi: 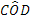
Tesi: 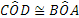
Dimostrazione
Gli angoli 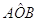 sono angoli adiacenti dato che hanno un lato in comune e gli altri due lati sono l’uno il prolungamento dell’altro.
sono angoli adiacenti dato che hanno un lato in comune e gli altri due lati sono l’uno il prolungamento dell’altro.
Ma anche gli angoli  sono angoli adiacenti per lo stesso motivo.
sono angoli adiacenti per lo stesso motivo.
Quindi gli angoli  e cioè la tesi.
e cioè la tesi.
►7. Perpendicolari e altre definizioni
DEFINIZIONE. Due rette si dicono perpendicolari se sono incidenti e formano quattro angoli retti.
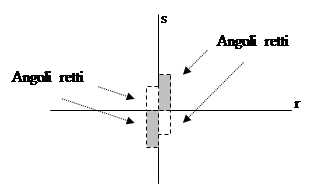
Figura 59. Le rette r e s sono perpendicolari, incontrandosi formano quattro angoli retti.
Per indicare che le due rette r e s sono perpendicolari si usa il simbolo 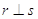 .
.
DEFINIZIONE. Si dice distanza di un punto da una retta il segmento di perpendicolare condotta dal punto alla retta.

Figura 60. Il segmento PH, appartenente alla perpendicolare a r passante per P, è la distanza di P dalla retta r.
DEFINIZIONE. Si dice asse di un segmento la retta perpendicolare al segmento e passante per il punto medio del segmento.

Figura 61. La retta r è l’asse del segmento AB in quanto è perpendicolare alla retta per AB e passa per il punto medio di AB.
DEFINIZIONE. Due punti si dicono punti simmetrici rispetto a una retta se la retta è asse del segmento che ha per estremi i due punti.
Nella figura 61, i punti A e B sono simmetrici rispetto alla retta r.
48 Completa la frase:
Quando si parla di angolo acuto o di angolo ottuso, bisogna saper eseguire l'operazione di ............................. tra angoli e aver dato la definizione di ..……….............
49 Due angoli sono complementari e uno è doppio dell'altro. Allora:
[a] uno è retto e l’altro è piatto
[b] uno è 1/3 dell’angolo retto e l’altro i 2/3 dell’angolo retto
[c] uno è 1/3 dell’angolo retto e l’altro 1/6 dell’angolo retto
[d] uno è 1/2 dell’angolo retto e l’altro è retto
[e] uno è 2/3 dell’angolo retto e l’altro i 4/6 dell’angolo retto
50 Se α e β sono due angoli di vertice O, consecutivi e complementari e a e b le loro bisettrici, allora per l'angolo 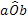 si può dire che:
si può dire che:
[A] è uguale all'angolo retto [B] è la terza parte di un angolo retto
[C] è la metà di un angolo retto [D] è la quarta parte di un angolo retto
[E] non è possibile determinarne l'ampiezza
51 Le bisettrici di due angoli adiacenti:
[A] sono parallele [B] sono lati di un angolo retto
[C] sono lati di un angolo concavo [D] coincidono
[E] sono semirette opposte
52 Due angoli si dicono complementari quando:
[A] sono consecutivi [B] sono angoli opposti al vertice
[C] la loro somma è un angolo retto [D] ciascuno di essi è acuto [E] ciascuno è la metà di un angolo retto
53 Dati due segmenti adiacenti AB e BC tali che 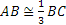 , allora per AC = AB + BC si può dire:
, allora per AC = AB + BC si può dire:
[A] 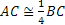
[C] 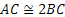
[E] 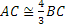
54 Due segmenti AB e CD appartengono alla stessa retta e hanno lo stesso punto medio. Si può affermare:
[A] 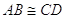
[C] 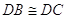
[E] 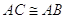
55 Per ciascuna delle affermazioni seguenti, dire se è vera o falsa, e spiegare perché
[A] l'angolo retto è la metà dell'angolo giro
[B] ogni angolo convesso ha due bisettrici
[C] due angoli che hanno in comune il vertice sono consecutivi
[D] un angolo ottuso è maggiore di qualunque angolo acuto
[E] sommando due angoli acuti si può ottenere un angolo piatto
56 Tre semirette a, b, c uscenti da uno stesso punto dividono il piano in tre angoli congruenti. Dopo aver rappresentato le semirette, traccia la semiretta b1 opposta di b. Allora:
[A] b1 è perpendicolare alla semiretta a
 [B] b1 è bisettrice dell’angolo formato da a e c
[B] b1 è bisettrice dell’angolo formato da a e c
[C] b1 è perpendicolare alla semiretta c
57 Dato l’angolo acuto 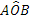 , sia OC la sua bisettrice. Sia poi OD una semiretta esterna all’angolo come in figura, quale relazione è vera?
, sia OC la sua bisettrice. Sia poi OD una semiretta esterna all’angolo come in figura, quale relazione è vera?
[A]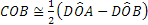
[B]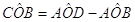
[C]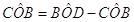
[D] 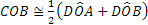
58 Perché se due angoli sono complementari i loro doppi sono supplementari?
59 In un piano gli angoli 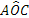 è retto.
è retto.
60 Un angolo α è retto e un angolo β è la sesta parte di un angolo piatto. A quale frazione di angolo retto corrisponde la somma α+β?
61 Quattro semirette con origine nello stesso punto dividono un angolo giro in quattro angoli α, β, γ, δ disposti in senso antiorario secondo l’ordine alfabetico. Si sa che α è congruente a γ e β è congruente a δ. Dimostra che ci sono alcune semirette opposte, quali sono?
62 Quando due angoli sono complementari? Disegna un angolo convesso e i suoi complementari consecutivi, spiega come hai costruito gli angoli complementari. Spiega perché i complementari dello stesso angolo sono congruenti.
63 Disegnare due angoli consecutivi α e β, disegnale l’angolo γ adiacente a α non contenente β e l’angolo δ adiacente a β non contenente α. Gli angoli γ+δ e α+β sono:
[A] complementari [B] supplementari [C] opposti al vertice [D] esplementari
64 Sia M il punto medio del segmento AB e sia P un punto compreso tra M e B. Che relazione esiste tra MP e la differenza AP-BP? Per aiutarti costruisci il punto Q tale che 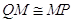 .
.
65 Sia 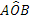 .
.
5. LA MISURA
►1. Misura di segmenti
Riprendiamo alcune definizioni sui segmenti:
Si dice segmento di estremi A e B (o brevemente segmento AB) l’insieme dei punti A e B e di tutti quelli che stanno tra A e B.
Due segmenti AB e CD si dicono congruenti se esiste un movimento rigido che porta a coincidere A con C e B con D, oppure A con D e B con C. Ricordiamo che se esiste un movimento rigido che porta a coincidere A con C e B con D allora esiste anche un movimento rigido che porta a coincidere A con D e B con C, e viceversa. È altresì vero che, anche nel caso in cui i due segmenti appartengano alla stessa retta, uno dei due movimenti comporta il “ribaltamento” di uno dei due segmenti che gli fa occupare posizioni al di fuori della retta che lo contiene.
Si dice lunghezza di un segmento AB l’insieme di tutti i segmenti congruenti ad AB.
Si dice distanza tra due punti A e B il segmento AB di estremi A e B.
Diamo ora una definizione particolarmente importante per l’applicazione del calcolo numerico alla geometria: la definizione di misura. Ricordiamo che la nozione di misura è alla base delle applicazioni del calcolo matematico non solo alla geometria ma anche alla fisica e alla tecnologia in generale. Il processo di misurazione è analogo a tutti i campi di applicazioni: si tratta di trovare un modo per assegnare a una grandezza un numero. Questo numero si ottiene confrontando due grandezze dello stesso tipo. Per esempio, per misurare la massa di un oggetto si confronta la sua massa con quella di un oggetto campione, di solito un oggetto di 1 kg.
Per misurare un segmento AB si confronta questo segmento con un altro segmento scelto come unità di misura, di solito indicato con u.
Nel confronto tra il segmento AB e il segmento u, possono verificarsi i tre casi seguenti:
- Il segmento AB è multiplo del segmento u secondo il numero naturale n, precisamente
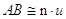

Figura 62. Il segmento AB misura 6u, in quanto 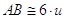 .
.
- Il segmento AB non è un multiplo intero di u ma è un multiplo di un sottomultiplo di u, precisamente
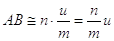 .
.
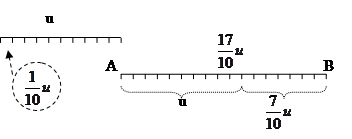
Figura 63. Il segmento AB è congruente a 17 volte il segmento 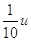 .
.
- Il segmento AB non è un multiplo né di u né di nessun sottomultiplo di u. In questo caso si dice che AB e u sono incommensurabili, nei casi precedenti si dice che sono commensurabili. Anche in questo caso è possibile attribuire ad AB un numero che ne esprime la misura rispetto a u, si tratta però di un numero irrazionale. La complessità dell’argomento richiede alcune conoscenze più avanzate di matematica, pertanto la tematica della misura delle grandezze incommensurabili sarà approfondita nel seguito. Qui ci accontentiamo di accennare al caso storicamente più noto di segmenti incommensurabili: la diagonale di un quadrato misurata rispetto al suo lato.
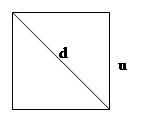
Figura 64. Prendendo come unità di misura il lato di un quadrato la sua diagonale è incommensurabile con il lato stesso. Applicando il teorema di Pitagora, ricorderai infatti che 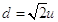 è un numero irrazionale.
è un numero irrazionale.
Proponiamo una dimostrazione dell’irrazionalità del numero 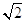 utilizzando il metodo della dimostrazione per assurdo.
utilizzando il metodo della dimostrazione per assurdo.
TEOREMA. 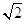 è un numero irrazionale.
è un numero irrazionale.
Dimostrazione
Supponiamo per assurdo che 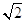 razionale. C.V.D.
razionale. C.V.D.
Un altro esempio di numero irrazionale, e di conseguenza di due “lunghezze” incommensurabili, è p, che rappresenta il rapporto tra la misura della lunghezza ‘rettificata’ di una qualsiasi circonferenza e la misura della lunghezza del suo diametro.
In generale, dato un segmento AB e un segmento u, preso come unità di misura, esiste sempre un numero reale positivo che esprime la misura di AB rispetto a u. Questo numero è unico, ossia ogni segmento ha una sola misura. Viceversa, dato un qualsiasi numero r reale positivo e un segmento u, preso come unità di misura, è sempre possibile costruire un segmento che misura esattamente 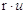 rispetto all’unità di misura fissata.
rispetto all’unità di misura fissata.
Osservazioni
- Se due segmenti sono congruenti, le loro misure, rispetto alla stessa unità di misura, sono uguali:
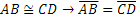 .
. - La misura di un segmento AB somma di due segmenti CD e EF (
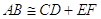 .
. - La misura di un segmento multiplo secondo n del segmento AB è uguale al prodotto di n per la misura di AB:
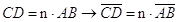 .
. - Definito il rapporto tra due segmenti come il quoziente tra le loro misure
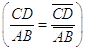 , rispetto alla stessa unità di misura, si ha che il rapporto non dipende dall’unità di misura usata per misurare i segmenti, cioè il numero che si ottiene è sempre lo stesso indipendentemente dall’unità scelta per misurare.
, rispetto alla stessa unità di misura, si ha che il rapporto non dipende dall’unità di misura usata per misurare i segmenti, cioè il numero che si ottiene è sempre lo stesso indipendentemente dall’unità scelta per misurare.
Possiamo pertanto parlare di misura della lunghezza di un segmento e darne la seguente definizione generale.
DEFINIZIONE. Dato un segmento AB e un segmento u, preso come unità di misura, si dice misura della lunghezza del segmento AB il numero reale positivo r per il quale 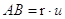 .
.
Nella realtà fisica per misurare la lunghezza degli oggetti reali (l’altezza di una persona, la lunghezza di un banco, di una stanza, di un terreno…) si usa come unità di misura il metro, indicato con m, con i suoi multipli (decametro, ettometro, chilometro…) e i suoi sottomultipli (decimetro, centimetro, millimetro…). Anche nella geometria, che tratta di segmenti ideali non riscontrabili perfettamente nella realtà, si usa come unità di misura un segmento di un metro.
Riassumendo, ricordiamo simboli e nozioni che riguardano due punti A e B.
- I due punti presi singolarmente, che con notazione insiemistica si indica con
 .
. - La retta passante per i due punti, che si indica con il simbolo
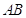 oppure r(A,B).
oppure r(A,B). - La semiretta di origine A e passante per B, che si indica con il simbolo
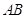 oppure r(A,B).
oppure r(A,B). - Il segmento di estremi A e B, che si indica con il simbolo
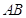 .
. - La distanza tra i punti A e B, cioè il segmento AB, che si indica con il simbolo
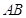 oppure d(A,B).
oppure d(A,B). - La lunghezza del segmento AB, cioè l’insieme di tutti i segmenti congruenti ad AB, che si indica con il simbolo
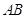 .
. - La misura della lunghezza del segmento AB rispetto a una fissata unità di misura, che si indica con il simbolo
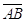 .
. - La misura della distanza tra i punti A e B, che corrisponde alla misura del segmento AB e si indica con il simbolo
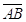 .
.
Tutte queste distinzioni sono importanti dal punto di vista dell’organizzazione teorica delle geometria, tuttavia dal punto di vista applicativo e della quotidianità del linguaggio geometrico possono risultare pedanti e noiose, spesso si usano espressione più generiche, finché si riescono ad evitare possibili malintesi. Sebbene a rigore si dovrebbe dire “La misura della lunghezza del segmento AB rispetto al centimetro è 12” molto spesso si usa dire “Il segmento AB è lungo 12cm” oppure “AB misura 12cm” o ancora “La distanza AB è lunga 12cm” o più semplicemente “Un segmento di 12cm” ecc.
66 Due segmenti adiacenti AB e BC misurano rispettivamente 12cm e 15cm, calcola la misura della distanza tra i loro punti medi M e N.
67 Dati due segmenti AB e CD, con 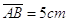 , sottrai dalla loro somma la loro differenza e verifica che si ottiene un segmento congruente al doppio del segmento minore.
, sottrai dalla loro somma la loro differenza e verifica che si ottiene un segmento congruente al doppio del segmento minore.
68 Il triplo di un segmento AB uguaglia il quadruplo di un segmento CD; determinare il rapporto tra AB e CD.
69 Due segmenti AP e PB sono tali che 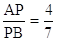 ; determina la misura del segmento AB=AP + PB, sapendo che AP misura 16cm.
; determina la misura del segmento AB=AP + PB, sapendo che AP misura 16cm.
70 I segmenti OA, AB e BC sono adiacenti; M ed N sono rispettivamente i punti medi di OA e di BC. Se 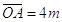 , quanto misura BC?
, quanto misura BC?
►2. Misura degli angoli
Il procedimento che si usa per misurare gli angoli è del tutto analogo a quello usato per misurare i segmenti. Si fissa una unità di misura, cioè un angolo  . Come risultato si avrà un numero reale positivo che chiamiamo misura dell’ampiezza dell’angolo.
. Come risultato si avrà un numero reale positivo che chiamiamo misura dell’ampiezza dell’angolo.

Figura 65. L’angolo 
Per misurare gli angoli l’unità di misura comunemente usata è la trecentosessantesima parte dell’angolo giro, quest’angolo si chiama grado, e si indica con un cerchietto posto in alto °. Si ha quindi, usando come unità di misura il grado, che:
- l’angolo retto misura 90 gradi, si scrive 90°;
- l’angolo piatto misura 180°
- l’angolo giro misura 360°.
I sottomultipli del grado sono il primo che è la sessantesima parte di un grado (in simboli 1°=60’) e il secondo che è la sessantesima parte del primo (in simboli 1’=60”) e quindi la tremilaseicentesima parte del grado (in simboli 1°=3600”).
Esempio
Calcola la misura in gradi del supplementare dell’angolo che misura 35° 15’ 40”.
Occorre eseguire la sottrazione 180°-35°15’40”. Per eseguire praticamente questa sottrazione si trasforma 1° in 60’ e 1’ in 60”, precisamente si scrive 180° come 179°59’60”, pertanto:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
7 |
9 |
° |
5 |
9 |
‘ |
6 |
0 |
“ |
- |
|
|
|
3 |
5 |
° |
1 |
5 |
‘ |
4 |
0 |
“ |
= |
|
|
1 |
4 |
4 |
° |
4 |
4 |
‘ |
2 |
0 |
“ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Quindi 180° - 35°15’40” = 144° 44’ 20”.
Il sistema di misura degli angoli che abbiamo illustrato prende il nome di sistema sessagesimale. Spesso, però, per praticità, anziché usare i primi, i secondi e i decimi di secondo, si usano i decimi di grado: in questo caso il sistema si dice sistema sessadecimale.
In base a quanto abbiamo illustrato, vediamo brevemente come si passa da un sistema all’altro.
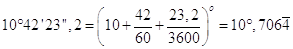 .
.
I sistemi sessagesimale e sessadecimale non sono gli unici usati per le misure degli angoli.
Osservando i tasti di una calcolatrice scientifica, si può vedere che ci sono tre sistemi principali le cui unità sono rispettivamente il grado sessagesimale (DEG), il grado centesimale (GRAD) e il radiante (RAD).
Il grado centesimale è importante per gli strumenti tecnici. Si può passare dal grado sessagesimale al grado centesimale e viceversa con una semplice proporzione, sapendo che l’angolo retto, pari a 90°, corrisponde a 100 gradi centesimali (in simboli 100g).
Il radiante è utile nello studio della trigoniometria e dell’analisi matematica. L’angolo di misura 1 radiante (in simboli 1 rad) è congruente ad un angolo con vertice nel centro di una circonferenza e tale che la misura dell’arco da esso individuato è uguale alla misura del raggio della circonferenza stessa. Come si può facilmente intuire, il radiante ed il grado sono grandezze incommensurabili.
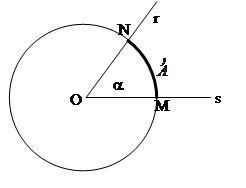
Figura 66. L’angolo α formato dalla semiretta ON e OM misura 1 radiante se l’arco 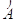 misura quanto il raggio della circonferenza.
misura quanto il raggio della circonferenza.
La misura di un arco va fatta con una modalità differente rispetto a quella utilizzata per la misura dei segmenti. Si può immaginare di utilizzare come strumento di misura un metro flessibile, ovvero un filo flessibile ma inestensibile, che si può piegare ma non si può allungare o accorciare, su cui siano state tracciate a distanza regolare delle tacche corrispondenti a sottomultipli dell’unità di misura delle lunghezze; una di queste tacche viene assunta come origine del metro. Facendo combaciare l’origine del metro flessibile con il punto M e flettendo il metro in modo che si sovrapponga all’arco MN si otterrà dell’arco  .
.
Ricordando che il rapporto tra la misura della circonferenza ed il raggio vale 2p, dove p è il numero irrazionale 3,1415… (i puntini indicano che la parte decimale è infinita e non periodica), possiamo intuire che il valore dell’angolo giro (360°), corrispondente ad un arco che coincide con l’intera circonferenza, vale 2p radianti.
Diamo ora una tabella che fornisce i valori degli angoli più comuni espressi in radianti:
angolo |
angolo |
360° |
2p |
180° |
p |
90° |
p/2 |
60° |
p/3 |
30° |
p/6 |
45° |
p/4 |
270° |
3p/2 |
71 Calcola la misura dell’ampiezza di due angoli di cui si sa che sono complementari e che la loro differenza misura 12°30’.
72 Calcola la misura di due angoli adiacenti, di cui si sa che uno è 3/4 dell’altro.
73 Un angolo che sia i 3/5 di un angolo giro misura:
[A] 72° [B] 216° [C] 330° [D] 550°
74 Se ad un angolo retto sommo i suoi 5/3 ottengo un angolo la cui misura è:
[A] 240° [B] 150° [C] 144° [C] 125°
75 Le quattro semirette a, b, c, d hanno la stessa origine O e sono disposte in senso antiorario; m è la bisettrice sia dell’angolo  ?
?
►3. Angoli negativi
Nei paragrafi precedenti abbiamo definito l'angolo come l’insieme dei punti compresi tra due semirette aventi la stessa origine O.
Possiamo però definire l’angolo anche come rotazione di una semiretta intorno alla propria origine, la misura di un angolo diventa allora la misura dell’entità della rotazione.
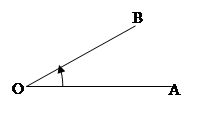
Figura 67. L’angolo può essere definito come rotazione di una semiretta intorno alla sua origine.
Dal momento che una rotazione può essere effettuata in due versi, orario od antiorario, si assume uno dei due versi di rotazione come positivo e l’altro negativo. Per motivi storici si è assunto come positivo il verso di rotazione antiorario e negativo quello orario.
Da questa definizione segue che  è l'angolo formato dalla semiretta AO rispetto alla semiretta OB.
è l'angolo formato dalla semiretta AO rispetto alla semiretta OB.
Inoltre la misura dell’angolo è definita a meno di un multiplo intero di 360°, ovvero gli angoli α e α+360° hanno la stessa ampiezza, lo stesso dicasi per tutti gli angoli del tipo 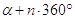 con n intero.
con n intero.
Per esempio, sono congruenti gli angoli di 45°, di 405°, 765°,…
6. POLIGONALI E POLIGONI
►1. Poligonale
DEFINIZIONE. Si chiama spezzata una figura formata da una sequenza ordinata di segmenti uno consecutivo all’altro. I segmenti che formano la spezzata si chiamano lati, gli estremi dei segmenti si chiamano vertici.
Ogni vertice è quindi in comune a due lati, ad eccezione del primo vertice del primo segmento e dell’ultimo vertice dell’ultimo segmento che possono appartenere a un solo segmento.
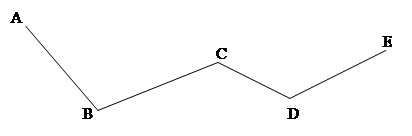
Figura 68. La linea ABCDE è una spezzata, perché formata da segmenti consecutivi. I segmenti AB, BC, CD, DE sono i lati della spezzata, i punti A, B, C, D, E sono i vertici.
DEFINIZIONI. Un spezzata si dice spezzata chiusa se il primo estremo del primo segmento coincide con l’ultimo estremo dell’ultimo segmento; si dice spezzata aperta se il primo estremo e l’ultimo estremo sono distinti.

Figura 69. Le figure F1 e F2 sono spezzate aperte in quanto hanno il primo e l’ultimo vertice che non coincidono; le figure F3 e F4 sono spezzate chiuse in quanto tutti i vertici appartengono a due lati consecutivi.
DEFINIZIONI. Un spezzata si dice intrecciata se almeno due suoi lati si intersecano in punti diversi dagli estremi; si dice semplice o non intrecciata se ogni coppia di lati non consecutivi non ha punti in comune.
G

Figura 70. La figura F1 è un spezzata aperta intrecciata (gli estremi A e D non coincidono, i lati CD e AB si intersecano); la figura F2 è una spezzata chiusa intrecciata (ogni vertice è in comune a due lati, i lati AB e DE si intersecano); la figura F3 è una spezzata aperta semplice (gli estremi A ed F non coincidono, non ci sono lati non consecutivi che si intersecano); la figura F4 è una spezzata chiusa semplice (ogni vertice è in comune a due lati, non ci sono lati non consecutivi che si intersecano).
DEFINIZIONE. Si chiama poligonale una spezzata chiusa non intrecciata.
►2. Poligono
DEFINIZIONI. Si chiama poligono la figura formata da una poligonale e dalla parte finita di piano da essa delimitata.
In un poligono chiamiamo:
- vertici del poligono i vertici della poligonale;
- lati del poligono i lati della poligonale;
- contorno del poligono la poligonale stessa;
- punti interni i punti del poligono non situati sul contorno;
- punti esterni tutti i punti del piano che non sono interni e non appartengono al contorno;
- perimetro del poligono il segmento somma dei lati del poligono.
DEFINIZIONE. Un poligono si dice poligono convesso se è una figura convessa, cioè se il segmento che ha per estremi due suoi punti qualsiasi è interamente contenuto nel poligono, si dice concavo se non è convesso, cioè se esistono almeno due punti per i quali il segmento che li unisce non è contenuto interamente nel poligono.
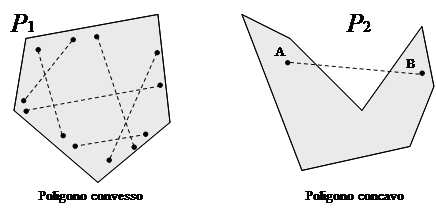
Figura 71. Il poligono P1 è convesso perché comunque si prendono due suoi punti interni, il segmento che li unisce è interno al poligono; il poligono P2 è concavo perché il segmento AB cade in parte all’esterno del poligono.
Nel seguito quando parleremo di poligoni intendiamo sempre poligoni convessi.
In un poligono chiamiamo:
- angolo interno o angolo del poligono ognuno degli angoli che ha per lati le semirette che contengono due lati consecutivi del poligono e ha per vertice il vertice del poligono in comune a quei due lati;
- angolo esterno è ciascun angolo adiacente ad un angolo interno.
Osservazioni
- Un poligono è convesso se ogni angolo interno è convesso.
- Un poligono è concavo se ha almeno un angolo interno concavo.

Figura 72. Nella figura a sinistra sono indicati gli angoli interni al poligono, nella figura di destra sono indicati gli angoli esterni, ognuno di essi è adiacente a un angolo interno.
Osserva che per ogni angolo interno esistono due angoli esterni, congruenti tra di loro perché opposti al vertice, ovvero perché supplementari dello stesso angolo.

Figura 73. Ogni angolo interno ha due angoli esterni adiacenti ad esso.
Inoltre definiamo:
- corda ogni segmento che unisce due qualsiasi punti del contorno del poligono che non appartengono allo stesso lato;
- diagonale ogni corda che unisce due vertici non consecutivi.
Figura 74. Il segmento AB è una diagonale del poligono poiché unisce i vertici non consecutivi A e B; il segmento DC è una corda poiché unisce due punti posti su due lati distinti del poligono.
I poligoni hanno nomi diversi a seconda del loro numero di lati:
- triangolo è un poligono con tre lati;
- quadrilatero è un poligono con quattro lati;
- pentagono è un poligono con cinque lati;
- esagono è un poligono con sei lati, e così via.
Un poligono si dice equilatero se ha tutti i lati congruenti tra di loro; si dice equiangolo se ha tutti gli angoli interni congruenti tra di loro. Un poligono che è equiangolo e equilatero si dice poligono regolare.
76 Quante diagonali ha un triangolo?
[A] nessuna [B] 1 [C] 2 [D] 3
77 Quante diagonali puoi tracciare dal vertice di un poligono di 6 lati?
[A] 6 [B] 5 [C] 4 [D] 3
78 Traccia l’angolo esterno relativo agli angoli interni indicati con un arco.
Copyright © Matematicamente.it 2010
 Questo libro, eccetto dove diversamente specificato, è rilasciato nei termini della Licenza Creative Commons Attribuzione - Non Commerciale - Condividi allo stesso Modo 2.5 Italia il cui testo integrale è disponibile al sito
Questo libro, eccetto dove diversamente specificato, è rilasciato nei termini della Licenza Creative Commons Attribuzione - Non Commerciale - Condividi allo stesso Modo 2.5 Italia il cui testo integrale è disponibile al sito
http://creativecommons.org/licenses/by-nc-sa/2.5/it/legalcode
Tu sei libero:
di riprodurre, distribuire, comunicare al pubblico, esporre in pubblico, rappresentare, eseguire e recitare quest'opera, di modificare quest'opera, alle seguenti condizioni:
Attribuzione — Devi attribuire la paternità dell'opera nei modi indicati dall'autore o da chi ti ha dato l'opera in licenza e in modo tale da non suggerire che essi avallino te o il modo in cui tu usi l'opera.
Non commerciale — Non puoi usare quest'opera per fini commerciali.
Condividi allo stesso modo — Se alteri o trasformi quest'opera, o se la usi per crearne un'altra, puoi distribuire l'opera risultante solo con una licenza identica o equivalente a questa.
Autori
Angela D’Amato: teoria, esercizi
Cristina Mocchetti: integrazioni, correzioni
Erasmo Modica: integrazioni
Claudio Carboncini: osservazioni
Germano Pettarin: correzioni
Nicola Chiriano: correzioni
Luciano Sarra: correzioni
Paolo Baggiani: integrazioni
Vittorio Patriarca: integrazioni
Giuseppe Pipino: correzioni
Anna Battaglini-Frank: osservazioni
Dorotea Jacona: correzioni
Antonio Bernardo: coordinamento
Collaborazione, commenti e suggerimenti
Se vuoi contribuire anche tu alla stesura e aggiornamento del manuale Matematica C3 o se vuoi inviare dei commenti e/o suggerimenti scrivi a antoniobernardo@matematicamente.it
Versione del documento
Versione 2.2 del 21.05.2010
Fonte: http://www.matematicamente.it/staticfiles/matematica-C3/GRC1-fondamenti-v2.2.doc
Geometria razionale nozioni fondamentali
Visita la nostra pagina principale
Geometria razionale nozioni fondamentali
Termini d' uso e privacy