Assonometrie e prospettive

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Assonometrie e prospettive

La geometria descrittiva, che può considerarsi un completamento dell’ordinaria geometria, raccoglie procedimenti e metodi che permettono di rappresentare figure geometriche a tre dimensioni su di un piano.
Le origini della geometria descrittiva sono pertanto antichissime e si confondono con quelle della architettura e della pittura. Si deve al matematico francese Gaspard Monge il merito di avere ordinato nel suo trattato “Géométrie descriptive” (Parigi, 1798) tutte le esperienze precedenti riguardo questa disciplina dandone una visione più organica e completa.

Se oggi l’importanza pratica della geometria descrittiva è diminuita a causa dello sviluppo di mezzi meccanici e ottici e per un diverso orientamento delle arti figurative, non si può dire altrettanto di quella teorica. Infatti il metodo della rappresentazione è ancora un valido strumento nella matematica moderna, nella quale spesso è più conveniente studiare le proprietà di determinate figure su loro rappresentazioni di più facile lettura.

Gli scopi che si prefigge la geometria descrittiva sono essenzialmente due:

Quello di disegnare su un piano p, detto quadro, una figura F' che riproduca le stesse sensazioni ottiche dell’oggetto F di cui è la raffigurazione. La F' si ottiene proiettando con rette uscenti da un punto O (centro di proiezione) i punti più significativi di F sul piano p ed è chiamata prospettiva di F da O su p. Se il centro di proiezione è

a distanza finita si ottiene il sistema delle proiezioni centrali o coniche
a distanza infinita si ottiene il sistema delle proiezioni cilindriche usato per le proiezioni ortogonali o assonometriche.

Se, da un lato, la raffigurazione di un oggetto, eseguita con una proiezione centrale, dà un’immagine di questo più simile a quella reale, dal momento che nella realtà il punto di vista non è mai a distanza infinita, dall’altro lato la proiezione parallela porta rette parallele in rette parallele, conserva i rapporti di lunghezza di segmenti allineati, quindi ad esempio porta i punti medi dei segmenti nei punti medi delle loro immagini, richiedendo così costruzioni più semplici di quelle della prospettiva.

quello della rappresentazione di F su p, cioè dell’introduzione su p di una figura F' con requisiti tali che la conoscenza di F equivalga a tutti gli effetti alla conoscenza di F'. Gioverà o potrà giovare la prospettiva F', ma questa non basta, perché un punto P di F individua il suo prospettico P' ma P' è prospettiva di tutti i punti della retta OP' proiettante. Un sistema di convenzioni e di notazioni che consente la piena sostituibilità di F con F' si dice un metodo di rappresentazione.

I metodi di rappresentazione più usati sono quelli

della doppia proiezione ortogonale (o di Monge),
delle proiezioni quotate,
della proiezione centrale
della proiezione assonometrica.

Elementi fondamentali delle proiezioni assonometriche

Gli elementi fondamentali per eseguire una assonometria possono essere riassunti nei seguenti quattro punti:

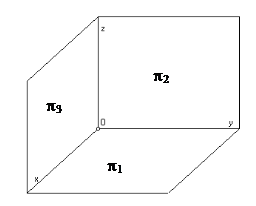
Un sistema di assi cartesiani ortogonali x, y, z di origine O che individuano il triedro fondamentale sul quale si immagina di porre l’oggetto che si vuole rappresentare in assonometria. Chiamiamo p1, p2, p3 rispettivamente il piano determinato dagli assi x ed y, dagli assi y, z e dagli assi x e z.

Per comodità si assumono gli assi x, y orizzontali, mentre l’asse z verticale.

Un pianop (quadro) sul quale proiettare l’oggetto ed il sistema di assi cartesiani x, y, z. Il piano p si suppone coincidente con il foglio sul quale si realizzerà la proiezione assonometrica.
Un segmento unitario u che rappresenta l’unità di misura reale.
Il centro di proiezione S¥ posto a distanza infinita e non appartenente al piano p, dal quale parte una stella di rette parallele, dette proiettanti, tangenti l’oggetto e incidenti il quadro.

Le proiettanti possono essere perpendicolari o no rispetto al quadro: nel secondo caso l’assonometria si dice obliqua, mentre nel primo è chiamata ortogonale.

Quando si esegue un'assonometria ortogonale, se la direzione di uno degli assi cartesiani x, y, z coincide con quella del centro di proiezione S¥, l’immagine di tale asse sul quadro sarà un punto. Inoltre se la direzione del centro di proiezione S¥ appartiene ad uno dei piani pi (i=1, 2, 3) le immagini delle rette appartenenti a questo piano (o a piani paralleli ad esso) risultano sovrapposte ed in particolare risultano sovrapposti gli assi cartesiani appartenenti al piano stesso (o coppie di rette incidenti, parallele a tali assi). Per questo motivo quando si esegue un'assonometria ortogonale se il quadro p è parallelo ad uno o a due degli assi cartesiani x, y, z il disegno che si ottiene risulta illeggibile e di poca utilità.
Invece nel caso di un'assonometria obliqua se il piano p è parallelo ad uno dei piani pi (i=1, 2, 3) la figura situata sul piano pi', proiezione di pi, è identica a quella reale.
In particolare i due assi assonometrici, proiezioni degli assi cartesiani che individuano il piano pi parallelo a p, saranno ortogonali e le rispettive unità assonometriche saranno uguali all’unità di misura reale u.
Intersecando il triedro fondamentale con il piano assonometrico p si hanno i lati di un triangolo ABC detto triangolo fondamentale.
Il triangolo fondamentale ABC è sempre acutangolo.
Le proiezioni dei tre assi cartesiani x, y, z da S¥ su p sono tre rette x' , y' , z' uscenti dal punto O', proiezione del punto O, dette assi assonometrici.
Infine, a partire da O, si riporti su ognuno degli assi x, y, z e in un verso qualunque, il segmento unitario u. La proiezione su p dei tre segmenti unitari u individua tre segmenti ux', uy', uz', uscenti da O' e appartenenti rispettivamente agli assi x', y', z'. Tali segmenti, che in generale non sono più uguali tra loro né ad u, sono detti unità assonometriche, mentre i rapporti si chiamano rapporti di riduzione.
Se l'assonometria è ortogonale, ogni unità assonometrica è minore di u, se si esclude che la direzione del centro di proiezione coincida con quella di un asse e questo si richiede affinché si eviti la possibilità che risultino sovrapposte tutte le immagini appartenenti al piano stesso e che l'asse assonometrico risulti ridotto ad un punto.
Invece se l'assonometria è obliqua i detti rapporti possono avere valori qualsiasi, in quanto la proiezione parallela di un segmento è un segmento che può avere lunghezza minore, uguale o maggiore a quella del segmento stesso.

Nell'assonometria obliqua inoltre i vari elementi caratterizzanti la figura, quali gli angoli assonometrici, (formati dagli assi assonometrici presi a due a due) e le unità assonometriche sono indipendenti.

Questo fatto è garantito dal seguente teorema di POHLKE:
Tre segmenti complanari u1, u2, u3 uscenti da un medesimo punto O' e di lunghezze arbitrarie, formanti tra loro angoli arbitrari, possono considerarsi come proiezione parallela di tre segmenti uguali mutuamente ortogonali, purché non più di uno dei tre segmenti e non più di uno dei loro angoli sia nullo; questo comporta che la immagine bidimensionale di un cubo è la proiezione parallela di un cubo effettivo, purché spigoli paralleli abbiano immagini parallele.
Conseguenza immediata del teorema è che ogni assonometria conserva il parallelismo di rette e conserva il rapporto di segmenti paralleli, in pratica vale il teorema di Talete.

Assonometrie ortogonali

Le assonometrie ortogonali più usate sono:

assonometria ortogonale isometrica
assonometria ortogonale dimetrica
assonometria ortogonale trimetrica

Assonometria ortogonale isometrica

In questo tipo di assonometria il piano assonometrico p forma con gli assi cartesiani x, y, z rispettivamente gli angoli a, b, g tali che a = b = g.
Inoltre valgono le proprietà:

Le unità assonometriche sono uguali.
Il triangolo fondamentale è equilatero.
Gli angoli che gli assi assonometrici formano tra loro sono uguali.
Il rapporto di riduzione, uguale per tutti e tre gli assi assonometrici, assume il valore .

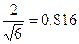Assonometria ortogonale dimetrica

In questo tipo di assonometria il piano assonometrico p forma con gli assi cartesiani x, y, z rispettivamente gli angoli a, b, g tali che a = b ¹ g (oppure a = g ¹ b oppure b = g ¹ a).
Inoltre valgono le proprietà:

Le unità assonometriche sono due uguali e una diversa e precisamente sono uguali le due unità relative agli assi che formano angoli uguali con p.
Il triangolo fondamentale è isoscele.
Gli angoli ).

Assonometria ortogonale trimetrica

In questo tipo di assonometria il piano assonometrico p forma con gli assi cartesiani x, y, z rispettivamente gli angoli a, b, g tali che a ¹ b ¹ g.
Inoltre valgono le proprietà:

Le unità assonometriche sono diverse tra loro.
Il triangolo fondamentale è scaleno.
Gli angoli 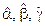che gli assi assonometrici formano tra loro sono diversi tra loro

Assonometrie oblique

Ci sono due tipi di assonometrie oblique più spesso usati di altri, sono:

L'assonometria cavaliera.
La proiezione militare.

Assonometria cavaliera

Nel caso in cui uno dei tre piani coordinati pi sia parallelo o coincidente con il piano assonometrico p, la proiezione obliqua assonometrica è detta assonometria cavaliera.

A causa della particolare posizione del piano p le proiezioni assonometriche degli assi cartesiani che individuano il piano pi parallelo a p, saranno due rette ortogonali e le relative unità assonometriche saranno uguali all’unità di misura reale u.
Il terzo asse assonometrico e la relativa unità di misura, invece, possono essere disegnati a piacere (per il teorema di Pohlke) rispetto ai primi due assi.
Per esempio, consideriamo il caso in cui il piano assonometrico p coincida (o sia parallelo) al piano p2 cioè al piano (yz). Gli assi assonometrici y' e z' formano un angolo di 90° e uy' = uz' =u.
Il terzo asse x' viene generalmente scelto coincidente con la bisettrice dell’angolo di 90° e la ux' è presa convenzionalmente uguale a u/2.
Questa particolare scelta di x' e ux' serve per avere una rappresentazione dell’oggetto più simile a quella reale.
Nella assonometria cavaliera sono conservate le sezioni parallele al piano assonometrico.

Proiezione militare

L’altro tipo di assonometria, chiamata “proiezione militare”, è caratterizzata dal fatto che le distanze verticali sono conservate, cosicché sono conservate le sezioni orizzontali, che risultano solo “scalate e ruotate” rispetto all’originale.
Nella figura a fianco sono rappresentati i cubi di lato unitario, detti cubi di riferimento, che servono a capire le proporzioni; in quella sotto due proiezioni dello stesso locale, coi due metodi assonometrici.

La proiezione militare è spesso usata nei videogiochi, in cui l'"eroe" deve visitare case o sotterranei alla ricerca dei mostri, dà una rappresentazione abbastanza chiara della conformazione, ma ha comunque zone d'ombra, date da pareti dietro le quali mostri o nemici si possono nascondere.

Prospettiva centrale

Si è detto che lo scopo della geometria descrittiva è quello di rappresentare le figure spaziali sopra un piano, in modo tale che, dalla rappresentazione piana, si possa risalire alla figura spaziale.
La corrispondenza tra una figura spaziale e la sua rappresentazione piana non è però purtroppo biunivoca, quindi permette solo di rappresentare le figure, ma non di risolvere graficamente, mediante solo costruzioni piane, problemi di geometria spaziale a meno di non introdurre altri eventuali dati aggiuntivi. Ciascuno dei sistemi di regole che permettono la rappresentazione piana costituisce un "metodo" della geometria descrittiva. Poiché, la parte principale di tutti i metodi più usati nel passaggio dalla figura spaziale alla sua rappresentazione, è costituita da una proiezione, tali metodi si chiamano anche metodi di proiezione.

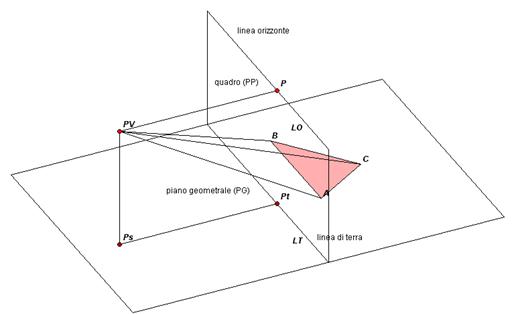ELEMENTI PRINCIPALI della prospettiva:

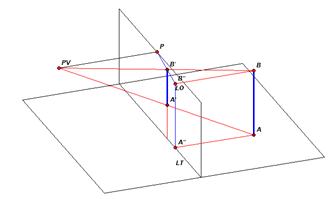
Punto di vista (PV): punto dove si immagina l’occhio dell’osservatore.
Piano di terra o geometrale (PG): piano sul quale è appoggiato l’oggetto da rappresentare.
Quadro o piano prospettico (PP): piano perpendicolare al piano di terra posto fra l’oggetto ed il PV; è su esso che si forma l’immagine in prospettiva dell’oggetto.
Piano di orizzonte (PO): piano immaginario passante per PV e parallelo al piano di terra.
Punto principale (P): proiezione ortogonale del punto di vista sul quadro detta anche distanza principale o semplicemente distanza perché indica la distanza dell’osservatore dal quadro
Punto di stazione (Ps): proiezione ortogonale del punto di vista sul piano geometrale
Linea di terra (LT): retta d’intersezione fra il quadro ed il piano di terra
Punto sulla linea di terra (Pt): proiezione ortogonale del punto principale e del punto di stazione sulla linea di terra
Linea di orizzonte (LO): retta d’intersezione fra il quadro ed il piano di orizzonte. Per costruzione è parallela alla linea di terra e la sua distanza da essa indica l’altezza dell’occhio dell’osservatore.
Raggi visuali: rette che congiungono il PV con i punti che costituiscono l’oggetto da rappresentare (quali ad esempio retta PV-A,PV-B,PV-C)

La scelta della posizione del punto di vista rispetto all’oggetto assume un’importanza fondamentale per la nitidezza della visione e per l’efficacia della prospettiva. In altre parole il punto di vista dovrà essere scelto in modo tale che la rappresentazione dell’oggetto che ne segue sia il più possibile simile alla rappresentazione reale. A tal fine è necessario tenere ben presente il campo visivo dell’osservatore cioè quella porzione di spazio misurata in gradi che una persona può vedere tenendo testa ed occhi assolutamente immobili.
Nella tecnica del disegno prospettico l’ampiezza del campo visivo si identifica nel cono ottico ottenuto tirando dal PV raggi visuali che hanno una ben precisa proprietà: non devono formare con l’asse visivo PV-P angoli maggiori di 30°.
Entro tali gradi, infatti, la percezione degli oggetti è buona e tale risulta essere anche l’immagine prospettica. Se invece si ampliasse il cono ottico in modo di avere angoli maggiori di 30°, si andrebbe incontro a delle particolari impostazioni prospettiche che deformerebbero l’immagine dell’oggetto in questione dando luogo alle cosiddette aberrazioni ottiche.
La base del cono ottico (il cerchio visivo) è determinato dall’intersezione dei raggi visuali con il quadro e si dice che l’immagine è “percettivamente corretta” quando i raggi visuali, portati agli estremi dell’oggetto, stanno all’interno del cono.

I punti di fuga

Il primo passo per costruire un’immagine prospettica è la ricerca dei punti di fuga. Il punto di fuga di una retta è la traccia sul quadro della parallela alla retta stessa passante per il PV. Poiché esso appartiene alla linea di orizzonte, che rappresenta in prospettiva l’immagine dell’infinito (tale infatti è la distanza tra LO e LT) il punto di fuga di una retta rappresenta la prospettiva del suo punto all’infinito. Da ciò discende immediatamente il fatto che rette parallele hanno il medesimo punto di fuga F.
In particolare:

Le rette parallele al quadro non hanno punti di fuga, o meglio ammettono come punto di fuga il punto improprio della linea d'orizzonte.

Esse sono rappresentate prospettivamente da rette tutte parallele fra loro ed alla LT; la loro distanza reciproca cambia al variare della distanza dal quadro prospettico.

Le rette perpendicolari al quadro hanno come punto di fuga il punto principale P. Se proviamo, infatti, a tracciare dal PV una parallela alla retta data incontreremo la LO in P.

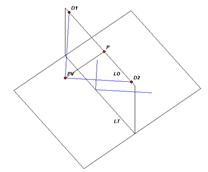Le rette inclinate di 45° rispetto al quadro hanno invece come punti di fuga punti particolari: essi sono denominati punti di distanza e sono le intersezioni del cerchio di distanza con la LO.

Le altezze in prospettiva

I segmenti perpendicolari al PG e quindi le altezze di solidi, edifici, ecc., rimangono tali in prospettiva.
Le lunghezze di tali segmenti dipendono dalla distanza che essi hanno rispetto all’osservatore.
Illustriamo ora il procedimento che si utilizza per realizzare la prospettiva di un segmento AB perpendicolare al PG.
Come primo passo costruiamo la prospettiva A' di A intersecando il raggio visuale PV-A con il quadro. In secondo luogo conduciamo da A la perpendicolare alla linea di terra che individuerà il punto A"; da tale punto tracciamo perpendicolarmente alla LT un segmento A”B” appartenente al quadro ed uguale ad AB. Uniamo B" con P; tale segmento interseca in B' la perpendicolare a LT per A'.
Il segmento A'B' così determinato risulta essere l’immagine prospettica di AB.
Si osserva che i triangoli PVAB e PVA'B' sono simili per costruzione.

I metodi usati in prospettiva centrale

Diversi sono i procedimenti usati in prospettiva per ottenere l’immagine prospettica di una figura ma tutti portano allo stesso risultato.
Nella prospettiva centrale i metodi più usati sono:

Il metodo dei raggi visuali
Il metodo del prolungamento dei lati
Il metodo dei punti di distanza
Il sistema di ribaltamento

Il metodo dei raggi visuali

Consideriamo il piano geometrale PG visto dall’alto; in questo caso la linea di terra LT coinciderà con la linea di orizzonte LO, il punto di vista PV con il punto di stazione Ps ed il punto principale P con il punto sulla linea di terra Pt.
Supponiamo di voler determinare l’immagine prospettica di un rettangolo.
Conduciamo quindi da PV i raggi visuali a ciascuno vertice del rettangolo; essi incontreranno LT rispettivamente nei punti A',B',C',D' e quindi proiettiamo ortogonalmente tutti i vertici del rettangolo sulla LT ottenendo i punti A"(=D"),B"(=C") (si noti che le coppie di punti A-D, B-C hanno la medesima proiezione)
Poniamo ora la nostra attenzione solo sul quadro ed uniamo con P le proiezioni dei vertici del rettangolo su LT appena ottenute ottenendo così le perpendicolari prospettiche del quadro. Costruiamo quindi i vertici dell’immagine prospettica ottenuti come punti di intersezione fra le perpendicolari alla LT passanti da A',B',C',D' e le perpendicolari prospettiche.
Immagine prospettica di un esagono regolare.
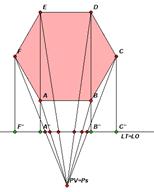Tracciamo dal PV i raggi visuali a ciascun vertice dell'esagono e chiamiamo A', B', C', D', E', F' le loro intersezioni con la LT (punti rossi).
Proiettiamo ortogonalmente tutti i vertici dell'esagono sulla LT ottenendo i punti F", A2(=E"), B"(=D"), C" (punti verdi) .
Sul quadro determiniamo i vertici dell'esagono intersecando le perpendicolari alla LT passanti da A', B', C', D', E', F' con le perpendicolari prospettiche ottenute unendo P a F", A", B", C" rispettivamente.

Il metodo del prolungamento dei lati

Come nel caso precedente consideriamo dapprima una visione dall’alto del piano geometrale.
Vediamo, mediante tale procedimento, come fare per determinare l’immagine prospettica di un esagono.
Una volta disegnato l’esagono prolunghiamo i lati EF e DC fino a determinare le rispettive tracce 1,2 sulla LT. Tracciando quindi da PV le parallele ai lati ne determiniamo i punti di fuga in Fs e Fd.
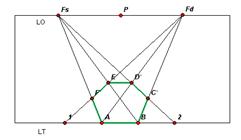Nel caso dell’esagono regolare in figura, in Fs concorrono i lati FA, DC e la diagonale EB; mentre in Fd i lati CB, EF e la diagonale DA.

Concentriamoci ora esclusivamente sul quadro e riportiamo su LO i punti P, Fs, Fd. Tracciando dai punti 1, 2, A, B le rette concorrenti ai rispettivi punti di fuga è possibile determinare tutti gli spigoli dell’esagono.

Nella figura sottostante si è ampliato il procedimento al fine di ottenere la prospettiva di una pavimentazione a maglia esagonale. Per ottenere ciò è sufficiente continuare a riportare sulla LT la misura del lato dell’esagono per l’estensione voluta.
È possibile completare il disegno in figura senza determinare ulteriori tracce sulla LT ma unicamente completando il prolungamento dei lati all’infinito.

Il metodo dei punti di distanza

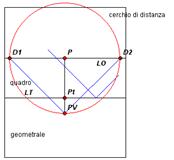
Questo metodo è basato sulla determinazione del cerchio di distanza come luogo geometrico dei punti di fuga delle rette inclinate di 45° rispetto al quadro.
Infatti per individuare il punto di fuga di una retta basta portare da PV una parallela alla retta stessa: se questa è una retta a 45° il suo punto di fuga D disterà dal punto principale P di una misura uguale a PV-P. Viceversa, disegnare sul quadro il cerchio di raggio PD significa determinare il cerchio di distanza e quindi i punti di fuga di tutte le rette a 45°.
Consideriamo quindi la nostra solita visione dall’alto dove l’oggetto da rappresentare in prospettiva è un quadrato e tracciamo da PV le rette inclinate di 45° rispetto alla LO determinando i punti di distanza D e D’. Per ciascun vertice del quadrato conduciamo le parallele ad una di queste rette (ad esempio la retta per D') e quindi proiettiamo A, B, C, E su LT ottenendo i punti A’(=E’) e B(=C’).

Consideriamo ora soltanto il quadro e riportiamo sulla LT i punti 1, 2, 3 e A', B' mentre sulla LO i punti D, P, D'. Congiungiamo 1, 2, 3 rispettivamente con D' e A', B' con P. Le intersezioni di queste ultime con forniscono i vertici del quadrato in prospettiva cercato.
Osserviamo infine che avremmo ottenuto la stessa figura prospettica se avessimo ripetuto lo stesso procedimento considerando le parallele alla retta per D.

Il sistema di ribaltamento

Tutti i metodi visti finora presentano, sostanzialmente, una grossa scomodità dovuta al fatto che, anche per determinare l’immagine prospettica di un oggetto molto semplice quale ad esempio un quadrato, bisogna ricorrere alla suddivisione del lavoro in due parti: la figura preparatoria sul PP e, in secondo luogo, la costruzione della figura prospettiva sul quadro.
Con il sistema di ribaltamento, per preparare l’esecuzione in prospettiva occorre ribaltare di 90° sia il semipiano su cui giace la figura, sia il semipiano su cui sta il punto di vista in modo che entrambi si trovino sullo stesso semipiano.
In altre parole, con tale procedimento, si riportano l’oggetto iniziale ed il PV sul medesimo semipiano in modo tale che quest’ultimo si possa considerare come il prolungamento del quadro sotto la LT.

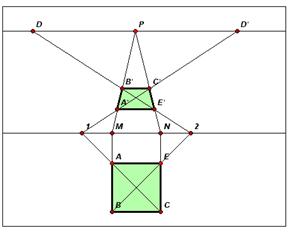
Nella fase esecutiva si proiettano sulla LT i punti significativi della figura che, in un secondo tempo, vengono uniti ai relativi punti di fuga mediante le rette proiettanti. L’intersezione delle linee proiettanti forniscono i punti che uniti fra loro determinano l’immagine prospettica dell’oggetto.
Osserviamo che l’oggetto da rappresentare, considerato nel semipiano sottostante al quadro, risulta rovesciato in pianta rispetto alla relativa immagine prospettica e che tali risulteranno essere anche le rette necessarie per determinare i punti di fuga.

Riassumendo, tre sono le caratteristiche di tale procedimento:

ci consente di vedere in modo istantaneo il variare dell’immagine prospettica al mutare delle dimensioni dell’oggetto considerato.
Possiamo vedere su un unico piano l’oggetto iniziale e la sua immagine prospettica (e quindi non abbiamo più la necessità di suddividere il lavoro)
Permette una notevole rapidità esecutiva.

Quest’ultimo metodo appena descritto appare pertanto come il più semplice ed allo stesso tempo il più completo nella determinazione delle immagini prospettiche.

La prospettiva accidentale

La prospettiva accidentale si differenzia da quella centrale per la diversa disposizione del quadro prospettico. Questo, in genere, non è parallelo ai lati dell’oggetto da rappresentare rispetto ai quali assume inclinazioni varie. Ciò dipende dagli effetti prospettici a cui si vuole giungere.
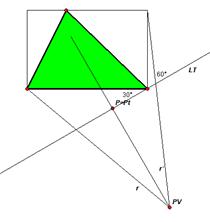Una buona prospettiva si ottiene disponendo il quadro nella figura preparatoria con inclinazioni diverse, per esempio 30°, 60° rispetto ai lati del rettangolo entro il quale è inquadrato l’oggetto, qualora lo stesso non presenti tali caratteristiche.
L’angolo minore è bene riferirlo al lato più importante della costruzione.
La scelta del punto di vista ha una parte predominante per la buona riuscita del disegno prospettico: la posizione è arbitraria ma è consigliabile porlo ad una distanza tale che l’angolo formato tra i raggi visuali r ed r', che dal PV vengono diretti verso gli estremi della figura rappresentata in pianta, sia contenuto attorno ai valori di 45°. In questo modo ci assicuriamo che i raggi visuali stiano all'interno del cono ottico e quindi che l'immagine risultante sia percettivamente corretta evitando così il fenomeno dell'aberrazione ottica.
L’ampiezza di tale angolo dipende sempre dalle dimensioni dell’oggetto da rappresentare in prospettiva. Inoltre è bene che il prolungamento della proiezione del PV sul quadro cada all’interno della pianta.

I metodi usati in prospettiva accidentale

Come la prospettiva centrale, anche la prospettiva accidentale ha i suoi procedimenti per determinare l’immagine prospettica dell’oggetto considerato. Essi sono:

Il metodo dei raggi visuali
Il metodo dei punti di distanza
Il metodo dei punti di fuga e delle perpendicolari al quadro
Il metodo dei punti misuratori

Osserviamo che i primi due metodi si utilizzano anche nella prospettiva centrale.

Il metodo dei raggi visuali

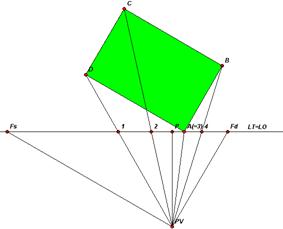Consideriamo dapprima il piano geometrale visto dall’alto e riportiamo la linea di terra LT (coincidente con LO), il punto di vista PV e la sua proiezione su LT Pt (coincidente con P).
Supponiamo di voler determinare l’immagine prospettica di un rettangolo ABCD.
Seguendo le ormai note operazioni preparatorie, si conducono dal PV le parallele ai lati del rettangolo di cui sopra che determinano i punti di fuga Fs ed Fd.
In essi concorrono rispettivamente tutte le rette parallele alle semirette che li hanno determinati.
Dal PV si conducono i raggi visuali verso i punti della pianta che intersecano la LT nei punti 1, 2, 3, 4 (si osservi che il punto 3 è coincidente con A).

Per la costruzione della prospettiva consideriamo il solo quadro e tracciamo su di esso la LT e la LO alla distanza che crediamo più opportuna.
Sulla LO riportiamo, nel rapporto stabilito, i punti di fuga e sulla LT i punti 1, 2, 3, 4.
Successivamente da 3 conduciamo le concorrenti a Fs e Fd che, intersecate dalle verticali condotte dai punti 1 e 4 riportati sulla LT, forniscono i punti D' e B'.
Poiché rette parallele hanno il medesimo punto di fuga, tracciamo da B' la retta per Fs e da D' la retta per Fd.
Queste ultime due rette si incontreranno nel punto C' che dovrà coincidere con la perpendicolare a LT tracciata dal punto 2.

Il metodo dei punti di distanza

Anche questo metodo ricalca fedelmente la costruzione fatta nel paragrafo precedente.
Consideriamo sempre il nostro piano geometrale visto dall’alto e costruiamo la prospettiva di un quadrato avente uno dei vertici appartenente alla LT.
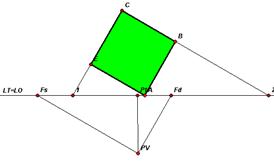Una volta scelto il PV, tracciamo sulla LT (coincidente con la LO) il punto Pt e i punti di distanza D e D'. Quindi dai vertici del nostro quadrato conduciamo le parallele alla retta passante per PV e D che intersecheranno la LT nei punti 1, 2, 3 rispettivamente.
Tracciamo poi le proiezioni dei vertici B, C, E sulla LT ottenendo i punti B', C' (coincidente con 1), E'.
Abbiamo così ottenuto tutti gli elementi essenziali per determinare la nostra immagine prospettica.
Poniamo ora la nostra attenzione esclusivamente sul quadro.
Riportiamo la LO con i punti P, D, D' e la LT su cui tracciamo i punti appena determinati.
Uniamo le proiezioni dei vertici con il punto principale P e congiungiamo i punti 1, 2, 3 con D.
Abbiamo così trovato i vertici B", C", E" dell’immagine prospettica cercata.

Il metodo dei punti di fuga e delle perpendicolari al quadro

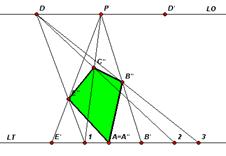Questo metodo si basa sul principio dell’individuazione di qualsiasi spigolo dell’oggetto attraverso la ricerca del punto di fuga della retta passante per esso.
Determiniamo la prospettiva di un quadrato iniziando a determinare i punti necessari alla costruzione sulla pianta.
Consideriamo la visione dall’alto del nostro piano geometrale.
Come primo passo determiniamo i punti di fuga Fd, Fs dei lati del quadrato tracciando dal PV rette parellele ad essi. Quindi prolunghiamo i lati del quadrato in modo da ottenere i punti 1, 2 come intersezione di questi ultimi con la LT.
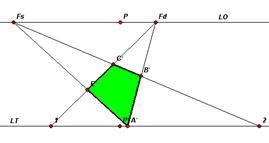Consideriamo ora solo il quadro e riportiamo i punti trovati sulla LT.
Uniamo A' (prospettiva di A) con Fs e Fd ottenendo così la prospettiva dei lati AE ed AB rispettivamente. In modo analogo congiungiamo il punto 2 con Fs ed il punto 1 con Fd ottenendo così la prospettiva dei lati BC ed EC rispettivamente. Per ultimare la figura basterà segnare le intersezioni di queste ultime rette che forniranno i vertici A', B', C', E' del quadrato prospettico.
Osserviamo che, qualora uno dei due punti 1 e 2 fosse risultato in pianta troppo lontano dal punto Pt, avremmo potuto trovare ugualmente la prospettiva della figura ricorrendo almeno ad altri due procedimenti. Il primo ricorre al metodo delle rette perpendicolari al quadro, il secondo si avvale dell'aiuto della geometria proiettiva. Applichiamo entrambi al nostro esempio.

Metodo delle rette perpendicolari al quadro

Supponiamo che il prolungamento del lato CB cada sulla LT troppo lontano e che quindi il punto 2 esca dal nostro piano di lavoro.
Per ovviare il problema consideriamo il vertice di tale lato che si trova più vicino alla LT (B) e proiettiamolo ortogonalmente su di essa. Otteniamo un nuovo punto 2'.

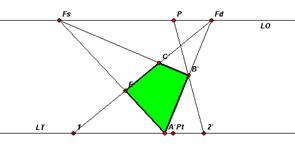Per la costruzione della figura si procede esattamente come in precedenza: uniamo i punti 1 ed A' con Fd e 2' con P. L’intersezione fra le rette A'Fd e 2'P fornisce il vertice B' del quadrato che una volta unito con Fs darà luogo al vertice C'.

Ricerca dell'asse di collineazione

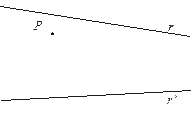Come è possibile congiungere un punto P con l’intersezione di due rette che si intersecano fuori del foglio di lavoro?
La geometria proiettiva, di cui non parliamo, serve a rispondere al problema. Tracciamo per P due segmenti che intersecano r ed r' in A e B e in A' e B' rispettivamente, in modo tale che le due rette AA' e BB' si intersechino nel foglio, in un punto O.

Ora tracciamo un'ulteriore retta per O, che intersecherà r e r' in C e C' rispettivamente. Intersechiamo i segmenti BC' e B'C, otterremo un punto Q. La retta PQ passa per il punto comune alle due rette (si chiama asse di collineazione della prospettività di centro O tra le due rette).

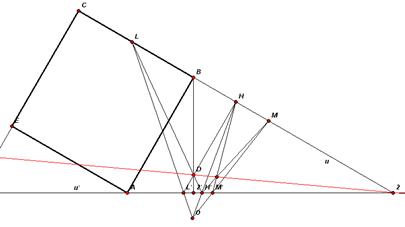Ecco l’immagine che illustra la costruzione della figura del cubo, se dobbiamo congiungere un punto D con il punto 2 fuori dal foglio.

Il metodo dei punti misuratori

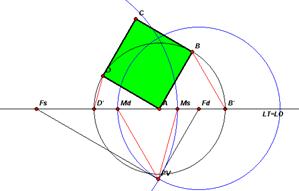Tutti i metodi finora descritti presentano una certa difficoltà nella riproduzione delle dimensioni reali dell’oggetto nell’immagine prospettica, infatti, le misure degli spigoli sono sempre proiettate sulla LT con rapporti di riduzione od ingrandimento e mai nelle loro dimensioni effettive.
Il metodo dei punti misuratori, che deriva direttamente da quello dei punti di fuga, supera queste difficoltà basandosi sui principi contenuti nel teorema di Talete sui segmenti proporzionali: rette parallele che intersecano due qualsiasi rette appartenenti allo stesso piano determinano, su queste ultime, segmenti proporzionali. Ne segue che le dimensioni dell’oggetto vengono riportate fedelmente od in modo proporzionale sulla LT.
Costruiamo quindi la figura preparatoria considerando la visione dall’alto del geometrale.
Una volta scelto il PV determiniamo sulla LT i punti di fuga Fs e Fd relativi ai lati AD (CB) e AB (DC) rispettivamente.
Centriamo quindi in Fs ed Fd e ribaltiamo il PV sulla LT dando luogo ai punti Ms ed Md rispettivamente. Successivamente centriamo in A e ribaltiamo i punti B e D sulla LT dando origine ai punti B’ e D’.
Poiché il segmento che congiunge B con B’ risulta parallelo al segmento che congiunge il PV con Md, quest’ultimo sarà il suo punto di concorso o misuratore.
Lo stesso vale per Ms che risulta essere il punto misuratore del segmento DD’ (parallelo al segmento PVMs)
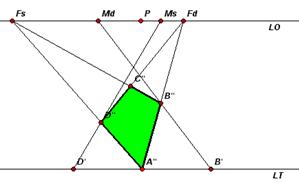Passando all’immagine prospettica, posizionati gli usuali elementi della prospettiva LO, LT, P, ed i punti di fuga Fs ed Fd riportiamo sull’orizzonte anche i punti misuratori Ms ed Md.
I punti misuratori sono punti di fuga che esercitano la loro influenza nelle porzioni di spazio in cui si sono eseguiti i ribaltamenti, per cui nel disegno prospettico, una volta determinate le linee principali della prospettiva (ovvero le rette AFs ed AFd) dobbiamo percorrere, dalle tracce sulla LT, le porzioni di spazio comprese fra la LT e le linee principali della prospettiva concorrendo ai propri misuratori situati dal lato opposto; nella restante porzione di spazio, compresa fra le AFs ed AFd, le rette concorreranno normalmente ai rispettivi punti di fuga.

Proiezioni di curve.

Consideriamo una curva in forma parametrica . Le sue proiezioni ortogonali sui piani coordinati si ottengono semplicemente sostituendo 0 al posto della variabile opportuna, quindi sono:

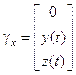
Su un piano parallelo ad un piano coordinato si ottengono sostituendo un opportuno valore numerico al posto della variabile opportuna.

Per proiettare una curva su un piano generico, il discorso si fa più complesso:
sia p: ax + by + cz + d = 0 l’equazione del piano.
Allora la generica retta, passante per un punto della curva e ortogonale al piano ha equazioni

e le equazioni parametriche della proiezione si ottengono intersecando r con p. Il conto può non essere banale; più semplice è determinare la matrice della proiezione: per far questo consideriamo il piano passante per l’origine e parallelo a p; tale piano ha equazione ax + by + cz = 0. Calcoliamo le proiezioni dei tre versori coordinati su tale piano ottenendo le colonne della matrice della proiezione: posto r = a2 + b2 + c2 è

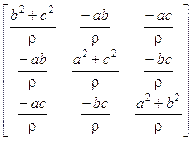
Si può verificare che tale matrice ha determinante nullo e così deve essere, poiché i trasformati dei tre vettori della base canonica sono dipendenti, in quanto complanari.
La matrice consente di trasformare qualsiasi curva; bisogna però tener conto del vettore traslazione, in quanto il piano dato non passava per l’origine.
Vediamo casi particolari di proiezioni.

Equazioni matriciali delle assonometrie

Per quanto detto, le assonometrie sono collineazioni, e sono tali da conservare il parallelismo di rette; questo comporta che sono omomorfismi dello spazio affine e che quindi possono essere espresse mediante matrici; poiché sono omomorfismi suriettivi di uno spazio affine di dimensione 3 su uno di dimensione 2, la matrice dell’omomorfismo deve avere rango 2.
Per costruire la matrice dell’omomorfismo, basta determinare i trasformati dei versori degli assi.
Per l’assonometria cavaliera risulta: i ® ; j ® i’ ; k ® j’ da cui la matrice è
.

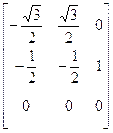
Per l’assonometria monometrica risulta invece: i ® ; k ® j'
quindi la matrice è
.
Si usa non scrivere la riga di zeri, quindi le equazioni matriciali sono rispettivamente:

Allo stesso modo si procede per le altre. Si ricordi che esiste un fattore additivo di traslazione, se l’origine O non viene trasformata nell’origine O'.
Come si è detto per le trasformazioni geometriche, è comodo conglobare la matrice della trasformazione affine e il fattore additivo di traslazione in un’unica matrice. L’equazione matriciale v’=Av+(Aw –w) ove w= è il vettore di traslazione, prende la forma
per le assonometrie.
Questa matrice viene chiamata in Computer Grafica matrice aumentata, ed è molto usata, come pure sono chiamate coordinate estese le coordinate di un punto.
Come vedremo nel caso della prospettiva, le coordinate estese (x, y, z, e), dove:
,
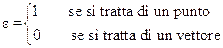hanno un importante significato geometrico.

Le prospettive dal punto di vista analitico

Osservando la figura a fianco si può notare che:

posto l’occhio dell’osservatore nell’origine del sistema di riferimento spaziale, in cui l’oggetto (pensato come puntiforme) ha coordinate (x, y, z),
posta l’origine del sistema di riferimento del quadro nel punto O' º (0, d, 0), per il teorema di Talete sulle parallele, le coordinate (x', y') dell’immagine sono legate alle coordinate dell’oggetto dalle seguenti proporzioni:

x : y = x': d e anche y' : d = z : y
da cui si ricava che
.
Queste relazioni consentono di trovare legami utili per i calcoli.
Il numero d è detto distanza oculare e controlla la dimensione dell’immagine.

Supponiamo ora invece che il quadro sia il piano zy (quindi abbia equazione x = 0).
Sia PV º (a, b, c) e sia P º (x’, y’, z’) il punto da proiettare.
La retta PVP ha equazioni parametriche
Tagliando col piano di equazione x = 0 si ricava da cui sostituendo si hanno le equazioni della proiezione:

Si osservi che il denominatore di tali frazioni non si annulla mai, a meno che il PV stia sul quadro, ma questo non può essere.
Come si vede, questa applicazione non è lineare, ma una razionale fratta, con numeratore e denominatore di primo grado, quindi la proiezione non è un omomorfismo dello spazio affine tridimensionale, come invece succedeva per le assonometrie. Inoltre, mentre le assonometrie (o proiezioni parallele) sono tali da conservare il parallelismo di rette (quindi, ad esempio, gli spigoli opposti di un cubo restano paralleli), questo non è vero per le prospettive, in cui restano parallele solo le rette “verticali”, cioè che rappresentano le rette dirette come l’asse z; anche per questo motivo le prospettive non sono affinità, e dunque non si possono esprimere mediante matrici 3×3 a determinante non nullo.
Sono comunque collineazioni, quindi si possono sì esprimere mediante matrici, ma del tipo 4×4 e poiché lo spazio viene trasformato nel piano, tali matrici avranno determinante nullo e rango 3; in realtà poi per comodità si usano addirittura matrici 3×4, sempre di rango 3.

Coordinate omogenee

Il discorso dovrebbe avere uno spazio e una profondità molto più ampia, ma vediamo il minimo indispensabile per comprendere i termini usati nella computer grafica.
Lo spazio che si ottiene è detto spazio proiettivo, ma, appunto, quella qui data è solo una visione ridotta.
Per quanto detto, si può, con opportune considerazioni, arrivare a costruire la matrice di una proiezione, pur di introdurre un sistema di coordinate completamente diverso.
Consideriamo il generico punto P º (x, y, z) dello spazio e poniamo

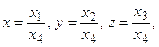
(naturalmente dobbiamo supporre che sia x4 ¹ 0 perché tale scrittura abbia un senso).

La quaterna (x1, x2, x3, x4) costituisce le coordinate omogenee del punto P.
Osserviamo, per come sono state costruite, che:

Quaterne proporzionali indicano lo stesso punto
Gli usuali punti dello spazio affine possono essere espressi in modo univoco come P º (x, y, z,1)
Le quaterne (x1, x2, x3,0) non hanno significato nello spazio affine.

Ora pensiamo, però, alle operazioni che facciamo sui punti, o meglio sulle loro coordinate:

se sottraiamo le coordinate di un punto P da quelle di un punto Q otteniamo le componenti del vettore ; dunque se P º (xP, yP, zP,1) e Q º (xQ, yQ, zQ,1) , risulta:

cioè possiamo pensare le quaterne (x1, x2, x3,0) come le componenti di un vettore che ha come direzione quella della retta per P e Q, quindi “un punto meno un punto fa un vettore”.

sommando ad un punto il multiplo (variabile con un parametro lineare) di un vettore (x = x0 + kv) si ottiene un punto variabile su una retta, quindi “un punto più un vettore fa un punto”.

Non ha senso invece sommare due punti.

Le coordinate estese dunque rappresentano:

i punti dello spazio proiettivo, i punti propri, cioè quelli dello spazio affine, se l’ultima coordinata è non nulla,
i punti impropri detti anche punti ideali sono i vettori, e individuano le direzioni delle rette, e hanno l’ultima coordinata nulla.

Nel piano proiettivo ci sono solo rette incidenti, o in un punto proprio (questa è la definizione affine d’incidenza), o in uno improprio (questa è la definizione affine di parallelismo); ricordando la teoria dei sistemi lineari, si ha, dette x, y, u, le coordinate estese di un punto del piano:

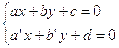
Nello spazio proiettivo, invece, sono sia rette incidenti o parallele (e quindi complanari) sia rette sghembe
Se consideriamo una retta dello spazio affine, di equazioni parametriche.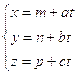
Più in generale una retta dello spazio proiettivo avrà la forma , ove h e k sono parametri omogenei. Tale retta passa per i due punti di coordinate omogenee (m, n, p, q) e (a, b, c, d).

In coordinate estese, la proiezione della figura precedente risulta avere equazione matriciale

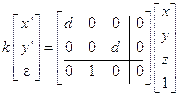
ove il fattore moltiplicativo k dipende dal fatto che terne (o quaterne) proporzionali danno lo stesso punto.

Un po' più complicato è trovare la matrice di ciascuna delle prospettive viste, ma il metodo è sempre il medesimo visto per le proiezioni parallele: si cercano le componenti dei vettori trasformati dei vettori della base e si considera il fattore additivo che dà l’eventuale movimento dell’origine, che non c’era nel caso visto.
Se la figura da trasformare è un poliedro (ad esempio un cubo) conviene trovare la matrice che ha per colonne le coordinate estese di tutti i vertici (e la matrice delle connessioni, per sapere quali segmenti disegnare). Il prodotto della matrice della proiezione per tale matrice dà le coordinate dei vertici trasformati; la matrice delle connessioni rimane la medesima.

Assonometrie e prospettive