Moto dei fluidi comprimibili

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Moto dei fluidi comprimibili

Gli aeriformi (gas e aeriformi) appartengono alla classe dei fluidi comprimibili poiché il loro volume massico varia con la temperatura e la pressione.

Lo studio del loro moto in un condotto; supposto permanente il regime, si può condurre basandosi sull’equazione di bilancio del sistema aperto e sull’equazione di continuità riferita alla portata massica per tenere conto del volume massico variabile .

Portata di efflusso in regime permanente

Si definisce “portata massica” la massa di fluido che attraversa una determinata sezione, normale all’asse geometrico della condotta, nell’unità di tempo.

G = S×V×r (1)

La portata massica G è misurata in kg/s se la massa volumica (r) viene espressa in kg/m3, se S rappresenta la sezione espressa in m2 e V la velocità in m/s.

Ricordando che la massa volumica è l’inverso del volume massico si ha:

r = 1/v

si perviene ad un’altra espressione della (1):

G =S×V/v (2)

dove ‘v’, volume massico, è misurato in m3/kg.

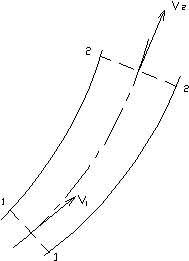Fig. (1)

Equazione di continuità

Se in una vena fluida comprimibile in regime permanente individuiamo due distinte sezioni, normali in ogni loro punto alla traiettoria dei filetti fluidi, rispettivamente di aree S1 ed S2, sulle quali le velocità assumono i valori V1 e V2 ed i volumi massici i valori v1 e v2, risulta:

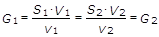(3)

Ciò significa che l’aeriforme che fluisce in una condotta a sezione variabile (S1¹S2) subisce variazioni di volume massico v e di velocità V tali da soddisfare sempre l’equazione (3).

1° Principio della termodinamica per i sistemi aperti o fluenti

Nel sistema aperto la vena fluida, in moto permanente nel condotto indeformabile (fig.1), scambia con l’ambiente esterno tanto energia termica Q quanto energia meccanica L, per cui il suo stato fisico (p, v, e T) tra le sezioni estreme (1-1) e (2-2) si modifica evolvendosi secondo una trasformazione.

Nel sistema chiuso il fluido è immobile e racchiuso in un contenitore deformabile, quindi a capacità variabile. Il primo principio della termodinamica viene scritto ovviamente in forme diverse per i due tipi di sistemi in quanto compiono lavoro in modo diverso.

Infatti nei sistemi chiusi, non essendoci scambio di materia con l’esterno, il fluido può compiere solo lavoro di deformazione elastica (o di deformazione) mentre nei sistemi aperti il fluido, contenuto in un condotto indeformabile, può compiere soltanto lavoro cinetico poiché possiede l’energia cinetica legata al moto del fluido che scambia materia con l’ambiente esterno.

Lo studio dei sistemi chiusi ha come applicazione le macchine termiche alternative, mentre i sistemi aperti hanno come applicazione le macchine termiche rotative.

Considerando l’espressione dell’entalpia possiamo giungere alla espressione analitica del primo principio della termodinamica per i sistemi fluenti.

h = U + p×v

Differenziando la quale si ottiene:

dh = dU + p×dv + v×dp

Questa espressione si trasforma considerando che:

dQ = dU + p×dv

per cui si ha:

dh = dQ + v×dp

da cui:

dQ = dh - v×dp

in forma finita:

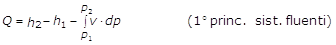(4)

Il lavoro cinetico si può quindi esprimere come:

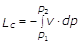(5)

Lc è positivo se la pressione diminuisce lungo la trasformazione.

Teorema di Bernoulli per gli aeriformi

Consideriamo un gas comprimibile in moto permanente dentro una tubazione ed applichiamo il principio della conservazione dell’energia fra due sezioni 1-1 e 2-2 scelte ad arbitrio (ma comunque normali all’asse geometrico). Si considera inoltre l’eventualità che nel tratto compreso tra le due sezioni venga scambiato con l’esterno una certa quantità di calore Q.

Fig.(2)

Con riferimento alla fig.2, la massa unitaria di fluido che attraverso la sezione 1-1 possiede le seguenti energie parziali:

- energia potenziale di posizione: g×z1 ;

- energia potenziale di pressione: p1 /r1 oppure anche: p1 v1;

- energia cinetica: ;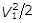

- energia interna: U1.

L’energia totale nella sezione 1-1 vale la somma delle energie parziali:

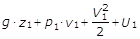
mentre ella sezione 2-2 l’energia totale vale:

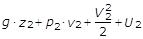
Il principio di conservazione dell’energia ci permette di affermare che l’energia totale della massa unitaria di fluido che attraversa la sezione 2-2 equivale a quella esistente nella sezione 1-1 aumentata del calore Q scambiato fra le due sezioni; tale bilancio deve essere peraltro definito nel tempo unitario. Deve essere perciò:

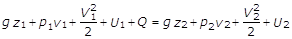(6)

Questa eguaglianza costituisce l’espressione analitica del teorema di Bernoulli applicato ad un fluido comprimibile.

Nel caso in cui il flusso dell’aeriforme avvenga in condizioni adiabatiche, tenendo conto che si può ritenere trascurabile la massa volumica per cui il termine della energia potenziale non si considera, si può scrivere l’espressione (6) nella forma:

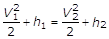(7)

Secondo la (7) nel caso di fluido adiabatico la somma dell’energia cinetica e dell’entalpia nella sezione 1-1 eguaglia la somma dell’energia cinetica e dell’entalpia nella sezione 2-2. Generalmente si preferisce però presentare la (7) sotto la seguente forma:

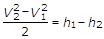(8)

Secondo la (8) la variazione di energia cinetica subita dall’unità di massa del fluido in una trasformazione adiabatica eguaglia il salto entalpico.

Rappresentazione grafica del lavoro cinetico

Nel piano (v, p) il lavoro cinetico (5) LC è rappresentato dall’area sottesa fra le linee di trasformazione 1-2 e l’asse verticale delle pressioni (fig.3). Infatti con riferimento ad una linea di trasformazione qualsiasi (1-2), seguita dal fluido entro il condotto fra le sezioni estreme 1-1 e 2-2 (fig. 2), consideriamo un tratto infinitesimo di quest’ultima tra le pressioni p e p-dp. Il volume massico lungo questo tratto può ritenersi costante per cui il rettangolino mistilineo tratteggiato in figura, di area infinitesima pari a v×(p-dp-p) = -vdp, non è altro che il lavoro cinetico infinitesimo. Estendendo quindi a tutta la trasformazione, tra gli estremi 1 e 2, otterremo il lavoro cinetico in forma finita

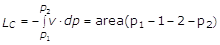(9)

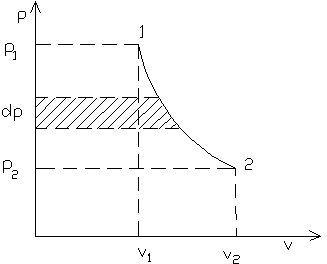Fig. (3)

Se nella equazione del primo principio per i sistemi fluenti consideriamo la quantità di calore scambiata con l’esterno eguale a zero possiamo scrivere che:

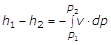(10)

essendo anche: 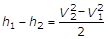, risulta:

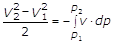(11)

In questo modo si giustifica il nome di lavoro cinetico dato dall’integrale del secondo membro.

Efflusso di un aeriforme: equazione di Saint Venant

Si dice che un aeriforme subisce un efflusso quando passa liberamente da un ambiente a pressione superiore ad uno a pressione inferiore per il solo effetto della differenza di pressione fra i due ambienti.

L’efflusso di un aeriforme può avvenire attraverso una luce oppure un ugello. Si chiama luce un foro praticato in una parete che separa due ambienti a pressione diversa; si dice ugello di efflusso un tronco di condotto, anch’esso separante due ambienti a pressione diversa, le cui pareti siano sagomate in modo da seguire il particolare andamento assunto dalla vena fluida effluente.

Studiamo ora l’efflusso da un serbatoio di un aeriforme, attraverso una luce in parete sottile (fig.4) in condizioni di regime permanente. I filetti di fluido, a partire da una sezione a monte della luce, convergono verso la luce stessa e oltrepassatala continuano, per effetto della velocità acquistata, a convergere fino ad una sezione posta a valle della luce in cui la vena assume la sezione minima: tale sezione prende il nome di sezione contratta.

Detta S l’area della luce e Sc quella della sezione contratta, si definisce coefficiente di contrazione il rapporto: j” = Sc / S.

Oltre la sezione contratta i filetti fluidi perdono continuità e la vena si rompe.

Fig.(4)

Consideriamo due sezioni, 1-1 e 2-2, in cui esistono le pressioni p1 e p2 con p2<p1 e supponiamo che non avvengano scambi di calore con l’esterno (efflusso adiabatico). Potremo in questo caso applicare la relazione (8) alle due sezioni. Se la sezione 1-1 viene scelta sufficientemente lontana dal foro di efflusso, potremo ritenere che in essa l’aeriforme sia in quiete (V1=0) mentre nella sezione 2-2, assunta in corrispondenza della sezione contratta, la velocità V2 sarà quella massima di efflusso.

Potremo quindi scrivere:

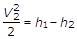
da cui:

(12)

La velocità di efflusso di un fluido comprimibile, nel caso di espansione adiabatica e resistenze nulle, dipende soltanto dal salto entalpico a cui è sottoposto il fluido tra gli stati fisici che esso assume dentro e fuori il serbatoio.

Weissbach determinò un’altra espressione della velocità di efflusso valida per i gas perfetti ma applicabile anche quando l’efflusso di un gas si può ritenere adiabatico, cioè senza apprezzabile trasmissione di calore attraverso le pareti del serbatoio, e quando il fluido defluisce in un ambiente sufficientemente grande così che la sua pressione non cambi per effetto della massa fluida entrante.

Il salto entalpico può essere valutato con l’espressione:

I1 - I2 = cp (T1 - T2) (13)

per cui sostituendo nella (12) avremo l’equazione di Weissbach:

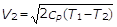(14)

Partendo dalla espressione (14) e tenendo conto che l’efflusso è adiabatico perveniamo ad un’altra espressione molto importante, detta di Saint Venant,che esprime la velocità di efflusso in funzione delle condizioni di pressione p1 e p2, rispettivamente a monte e a valle della luce di efflusso e del volume massico all’interno del serbatoio.

Ricordando che l’espressione della adiabatica tra le sezioni 1-1 e 2-2 è:

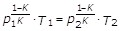
Da cui:

Essendo: p2=pE

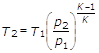
Sostituendo nella (14) si ottiene:

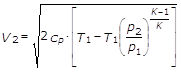
e mettendo in evidenza T1:

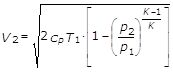(15)

Considerando l’espressione che lega le capacità termiche massiche e la costante caratteristica (cp=cv+R), la relazione cp/cv=g e l’equazione caratteristica dei gas, con una serie di passaggi si ottiene l’equazione di Saint Venant a partire dalla (15).

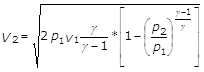(16)

La (16) rappresenta quindi l’equazione della velocità di efflusso teorica di un aeriforme o equazione di Saint Venant. Questa equazione è stata scritta considerando l’efflusso senza attriti. Per tenere conto delle resistenze passive bisogna introdurre nella (16) il coefficiente di riduzione delle velocità j’.

Equazione della portata di efflusso - Pressione critica

La portata massica effluente attraverso un foro si calcola, considerando sempre valida l’equazione di continuità G1=G2=G, con la seguente espressione:

(17)

dove V2 è la velocità di efflusso teorica, S è la sezione della luce, v2 il volume massico nella sezione contratta e j’’ è il coefficiente di contrazione della vena fluida.

Nella (17) non consideriamo gli attriti. Sostituendo nella (17) l’espressione trovata da Saint Venant per V2, si ottiene:

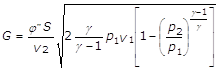
Esprimendo il volume massico v2 secondo la relazione: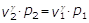

Dalla quale si deriva che:

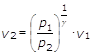
si ottiene:

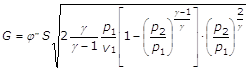(18)

La (18) rappresenta l’equazione della portata di efflusso.

Nel caso in cui si considerassero gli attriti diventa necessario introdurre nella (18) il coefficiente di efflusso:

m = j’ j’’

Osservando come nelle (16) e (18) sia G che V2 risultano funzioni di p2/p1, diventa possibile studiare l’andamento della portata in funzione di p2/p1 in modo da tracciare un diagramma, mettendo in ordinate la portata e in ascisse proprio il rapporto p2/p1.

Esaminando l’equazione, essa si annulla per p2/p1=1 e per p2/p1=0.

Nel diagramma questi punti di nullo li chiamiamo rispettivamente 0 ed M. Se andiamo a sostituire nella equazione della portata valori p2 decrescenti (partendo da p2=p1), dapprima la portata cresce (tratto O-L), poi deve diminuire (tratto L-M, tratteggiato) perché per p2=0 la (18) torna ad annullarsi. Il tratto L-M, come vedremo in seguito, non è reale nel fenomeno dell’efflusso di un aeriforme, per cui in questo schema è solo tratteggiato.

Determiniamo ora per quale valore del rapporto p2/p1 l’equazione della portata presenta un massimo. Affinché la portata G sia massima al variare di p2/p1, occorre ed è sufficiente che sia massima l’espressione:

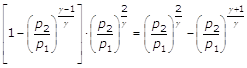(19)

Calcolando la derivata di tale espressione rispetto alla variabile p2 ed uguagliandola a zero si ottiene il valore del rapporto p2/p1 che rende massima la portata (sempre nell’osservazione dell’ipotesi p2=pE).

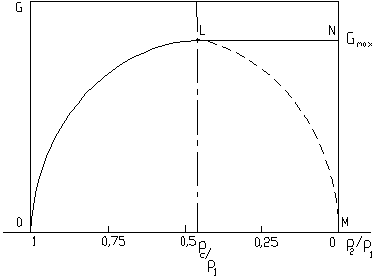Fig.(5)

Deriviamo la (19) ed eguagliamo a zero:

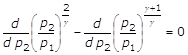
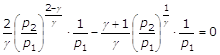
mettendo in evidenza il termine: :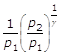

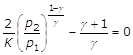
ossia:

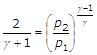
da cui:

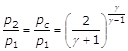(20)

ossia:

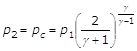(21)

La p2 calcolata con la (21) si dice “pressione critica” e viene indicata con pc. Il valore di p2/p1

calcolato con la (20) diventa quindi il “rapporto critico”, indicandolo con pc /p1. La pressione critica è quel valore di pressione che si stabilisce nella sezione contratta della vena fluida e rende la portata di efflusso massima.

Questo particolare valore della pc dipende solo dalle condizioni di pressione a monte dell’efflusso, cioè da p1, e dalla costituzione chimica dell’aeriforme, tramite il rapporto g tra le capacità termiche massiche a pressione costante e a volume costante.

Per i gas perfetti biatomici g vale 1.41, così che sostituendone il valore nella (21) si ottiene pc=0.528×p1; per gas monoatomici g vale 1.67 per cui pc=0.487×p1.

Sostituendo nella equazione della portata (18) il valore di pc ottenuto dalla (21), si otterrà il massimo valore di G:

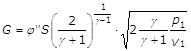(22)

Dalla espressione (22) si nota come il valore massimo della portata dipende solo dalle condizioni a monte dell’efflusso, come era prevedibile, essendo G massimo per p2=pc; mentre è inferiore alla massima per tutti i valori di p2>pc.

Velocità critica e del suono

Dalla equazione di Saint Venant si possono ricavare alcune interessanti considerazioni: la velocità di deflusso V2 aumenta al diminuire del rapporto p2/p1 e cioè quanto più alta è la pressione p1 dell’aeriforme all’interno del serbatoio rispetto alla pressione p2 che si stabilisce nella sezione contratta della vena fluida.

Esiste però un limite superiore della velocità di deflusso V2 oltre il quale la velocità resta costante. Questo limite superiore si chiama “velocità critica” (Vc) e dipende dalle condizioni termodinamiche dell’aeriforme all’interno del serbatoio, cioè a monte del foro di deflusso.

Il valore di velocità critica risulta essere la velocità del suono, la cui espressione è dovuta a Laplace:

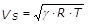(23)

in cui T è la temperatura dell’aeriforme.

Dimostriamo ora come il valore della velocità critica sia proprio la velocità del suono e come questa si raggiunga quando p2=pc.

Sostituendo nella equazione di Saint Venant a p2/p1 il valore del rapporto critico:

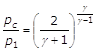
si ottiene l’espressione della velocità critica:

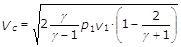
da cui:

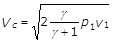(24)

L’equazione della adiabatica tra le sezioni 1-1 e 2-2 in termini di p e T, considerando in 2-2 le condizioni critiche, si scrive:

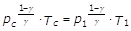
Essendo anche:

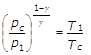
ovvero:

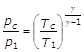
e sostituendo a pc/p1 il valore trovato nella (20):

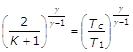
ovvero:

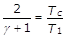
da cui:

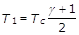(25)

Scriviamo l’equazione caratteristica dei gas nella sezione 1-1:

p1v1 = RT1 (26)

Sostituendo nella (26) il valore di T1 ricavato dalla (25):

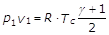(27)

L’espressione della velocità critica, data dalla (24), si modifica in virtù della (27):

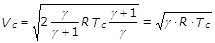(28)

Come si era premesso la velocità Vc è quindi uguale alla velocità del suono, cioè la velocità con cui si trasmettono le perturbazioni di pressione in una massa fluida. Possiamo definire a questo punto la pressione critica come quel valore della pressione per cui si stabilisce nella sezione contratta la velocità del suono.

La velocità nella sezione critica (contratta, dove p2=pc) raggiunge un massimo oltre il quale non può più aumentare. Se, infatti, a valle della sezione critica esistesse una pressione esterna pE<pc, questa perturbazione non potrebbe essere trasmessa al fluido in quanto essa stessa si muove alla velocità del suono.

Possiamo concludere che non potendosi trasmettere la perturbazione di depressione (pE <pc) a monte della sezione contratta il movimento del fluido dal serbatoio alla sezione contratta non subirà alcuna modificazione per la velocità e la portata continueranno a conservare il loro valore massimo, comunque si abbassi la pressione esterna pE. Questa spiegazione si deve a Hugoniot e Reynolds, da cui derivano i nomi delle espressioni che permettono di calcolare le relative grandezze fisiche.

Rappresentazione grafica della velocità di efflusso

In figura (6) rappresentiamo l’andamento della velocità di efflusso in funzione del rapporto delle pressioni.

Il tratto O-L-N, secondo quanto esposto in precedenza, è quello reale in quanto dapprima la velocità aumenta con il diminuire di p2/p1, quindi raggiunge un massimo uguale alla velocità del suono per il rapporto pc/p1. Nel tratto L-N si mantiene costante poiché il fluido non può superare la velocità del suono .

Il tratto L-M, teorico secondo Saint Venant, non è quindi reale quando l’efflusso avviene attraverso un foro. Vedremo, in seguito, che il tratto L-M può essere reale solo nel caso di espansione in un ugello De Laval convergente-divergente dove Vv rappresenta la velocità di efflusso nel vuoto per p2/p1=0.

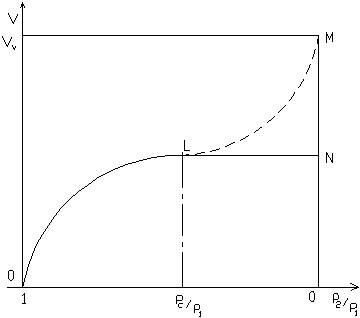Fig.(6)

Conclusioni

Riepiloghiamo quanto fin qui esposto, mettendo a confronto i risultati teorici delle equazioni (16) e (18) con i fatti.

Ricordiamo che p2 rappresenta la pressione sentita realmente dalla vena fluente nella sezione contratta. In precedenza con pE è stata indicata la pressione che regna nell’ambiente esterno ed è possibile notare che è stato sempre ammesso, implicitamente o esplicitamente nella trattazione teorica che ha portato a scrivere le equazioni di Saint Venant e della portata, che p2=pE. Si è supposto cioè che la vena all’uscita assuma la pressione dell’ambiente esterno. Questa ipotesi si dimostra in accordo con i fatti quando la pressione esterna pE è compresa tra il valore della pressione p1 nel serbatoio e il valore della pressione critica pc.

In questo caso infatti il valore della pressione p2 che la vena fluida assume nella sezione contratta coincide con la pressione esterna pE. Nell’equazione della portata, con p1=pE=p2, si ottiene infatti G=0. Il fluido cioè non esce attraverso la sezione di efflusso e nel diagramma di fig.5 si ottiene il punto 0.

In accordo con l’esperienza comune, infatti, quando la pressione esterna pE diminuisce il fluido comincia a uscire e la portata va poi crescendo (tratto 0-L, con p2³pC e p2=pE).

Continuando a diminuire la pressione esterna pE, ipotizzandola ancora uguale a p2, la portata dovrebbe diminuire (tratto L-M tratteggiato, con p2<pC e p2=pE).

L’ultima condizione, però, sembra strana ed è contraria ai fatti, quindi in questa circostanza l’assunzione che p2=pE si deve abbandonare.

L’esperienza afferma che quando la pressione pE scende al disotto della pressione critica pC il valore della pressione p2 nella sezione contratta rimane sempre p2=pC per cui p2¹pE, mentre la portata si mantiene costante con il valore massimo del tratto L-N (fig.5), essendo p2=pc.

In altri termini quando pE<pC la vena fluida non se ne accorge: il suo procedere è governato da monte e dipende quindi solo da p1, qualunque sia il valore della pressione pE che regna a valle, in questo caso risulta sempre p2=pC.

E’ anche vero che la vena fluida, sboccando nell’ambiente esterno, continua ad espandersi oltre la sezione contratta, ma questa perde la sua linearità, si frantuma in grossi vortici, il movimento diviene irregolare e il fluido si sparpaglia mescolandosi a quello dell’ambiente esterno, per cui la velocità e la portata non possono essere modificate da quello che avviene oltre la sezione contratta.

Ugelli di efflusso

Le luci, in parete sottile o grossa, vengono impiegate come strumenti di misura della portata, anche se questi organi si prestano male ad un loro impiego come effusori per trasformare il salto entalpico in energia cinetica. Principalmente il motivo per cui non vengono impiegati come effusori risiede nel fatto che la vena fluida non è seguita e guidata opportunamente da un condotto per cui per tener conto delle perdite dovute all’attrito dobbiamo introdurre un coefficiente di riduzione delle velocità abbastanza basso (j¢=0,6¸0,8).

Con questi valori di j¢ il rendimento dell’espansione risulta troppo basso. Infatti nelle applicazioni come organi di macchine (turbine a vapore, o a gas) l’espansione della vena fluida viene guidata da un condotto che può essere costituito da un solo tratto convergente (chiamato ugello convergente), oppure da un tratto convergente-divergente (o di De Laval).

Quanto esposto in precedenza sull’efflusso attraverso una luce rimane valido anche per gli ugelli, con l’osservazione che la velocità è sempre quella nella sezione terminale dell’ugello e che la caduta entalpica sfruttata è sempre quella corrispondente al salto di pressione fra monte e valle dell’ugello, mentre per la portata valgono le stesse considerazioni fatte per le luci.

Abbiamo visto che l’efflusso attraverso un foro presenta, oltre ad elevate perdite per attrito, anche un’altra notevole limitazione dovuta alla impossibilità di sfruttare salti entalpici elevati.

Infatti se a valle del foro esiste una pE<pc nella sezione contratta si stabilisce il valore della pressione critica (cioè p2=pC) per cui il salto entalpico che possiamo trasformare in energia cinetica vale solo (h1-hC) invece di (h1-hE).

Sappiamo però che nei cicli termodinamici per ottenere rendimenti elevati si devono sfruttare salti entalpici elevati. Il problema della completa trasformazione di notevoli salti entalpici in energia cinetica, utilizzando un unico ugello, fu risolto da De Laval.

De Laval pensò che dando la possibilità, in modo opportuno, al fluido di potersi espandere, oltre la sezione contratta in condizioni critiche, si poteva superare la velocità del suono, limite invalicabile per l’efflusso attraverso un foro o ugelli semplicemente convergenti.

Il concetto fondamentale in base al quale si riesce ad evitare gli inconvenienti dell’efflusso critico è quello guidare i filetti fluidi, senza rompere la continuità della vena fluida, con un tratto di condotto prima convergente e poi divergente. Quest’ultimo tratto è necessario affinché la vena di gas, o di vapore, si espanda regolarmente sotto la pressione critica.

Si possono, a questo punto, distinguere due regimi di efflusso:

1) regime subsonico, p2=pE>pC e la velocità è inferiore a quella del suono V2<VS;

2) regime supersonico, quando p2=pE<pC e la velocità è superiore a quella del suono V2>VS.

Concludendo, vediamo di riassumere in quali casi l’ugello dovrà essere sagomato solo convergente oppure convergente-divergente

In regime subsonico, cioè quando pE>pC, l’ugello sarà semplicemente convergente, la velocità di efflusso sarà minore della velocità critica e l’area della sezione terminale maggiore di quella che compete alle condizioni critiche.

In particolare se pE=p2=pC, l’ugello presenta un’area della sezione terminale uguale all’area della sezione critica, velocità di efflusso uguale a quella del suono e portata massima.

In regime supersonico, cioè con p2=pE<pC, l’ugello è costituito da due parti, fig.(7). Il tratto convergente arriva alla sezione contratta, SC, dove regna la pressione critica pC e la velocità del suono VS. Il divergente è un tronco di cono d’apertura uguale a circa 10° ed in esso il fluido seguita ad espandersi, fino a raggiungere il valore pE che regna nell’ambiente esterno.

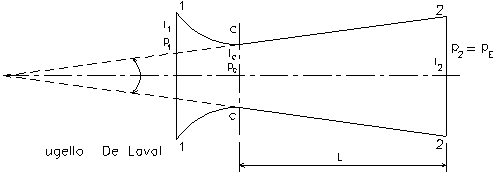Fig.(7)

La velocità V2 allo sbocco assume con ciò il valore corrisponde all’intero salto di pressione p1®pE e supera la velocità del suono. Il condotto di De Laval è uno dei pochi casi in cui la velocità cresce mentre pure la sezione cresce, circostanza che con un liquido (v=cost.) non può mai accadere.

Il regime permanente in una tubazione di un aeriforme si ha quando in una sezione generica della condotta le sue caratteristiche (p, T, v ) non variano nel tempo, pur differendo da punto a punto della sezione.

I sistemi termodinamici aperti sono quei sistemi in cui vi è flusso di massa attraverso il contorno; questi sistemi si dicono anche “sistemi fluenti”.

Oltre la condizione di moto permanente si introducono le seguenti ipotesi semplificative:

- filetti fluidi paralleli;

- uniformità dei valori delle grandezze di stato in ogni sezione, in altri termini si ammette che in tutti i punti di

una medesima sezione ortogonale ai filetti fluidi ciascuna delle grandezze di stato p, v e T abbia uguale valore;

- si ammette che il fluido abbia in tutta la sezione una velocità media uniforme.

Il lavoro LC è motore e cioè positivo quando la pressione diminuisce; mentre è negativo se la pressione è crescente lungo la trasformazione. Il ciclo nel primo caso viene percorso in senso orario e nel secondo caso in senso antiorario.

Supponiamo che la pressione esterna pE ,a valle del foro, sia uguale alla pressione p2 nella sezione contratta della vena fluida. In seguito vedremo che questo non è sempre vero.

Nel diagramma delle velocità, se si considera la linea a tratto continuo O-L-N bisogno prendere come ascissa lapressione esterna pE , poiché l’esperienza dimostra che non è più vera l’assunzione p2 = pE .

Nel diagramma della portata, se si considera la linea a tratto continuo 0-L-N bisogna prendere come ascissa il rapporto pE/p1.

Fonte: http://www.valentiniweb.com/piermo/meccanica/doc/1%20-%20fluidodinamica.zip

Moto dei fluidi comprimibili