• 
• 

 

Perdite di carico

 

 

---

 

Perdite di carico

 

I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

Perdite di carico

 

LE PERDITE DI CARICO

Argomenti trattati nella lezione:
PERDITE DI CARICO DISTRIBUITE...........................................................................................................
FATTORE DI ATTRITO...................................................................................................................................
DIAGRAMMA DI MOODY................................................................................................................................
PERDITE DI CARICO CONCENTRATE......................................................................................................
DIAMETRO EQUIVALENTE..........................................................................................................................
LUNGHEZZA EQUIVALENTE

 

PERDITE DI CARICO DISTRIBUITE

 

In un tubo in cui scorre un fluido le perdite di carico corrispondono alle perdite di pressione: per calcolarle si può utilizzare l’equazione che esprime la velocità in funzione della variazione di pressione 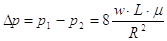(1).

                                             (1)

in cui w e m sono rispettivamente la velocità media e la viscosità del fluido, L ed R la lunghezza del condotto e il raggio della sua sezione.
La perdita di carico è quindi direttamente proporzionale alla viscosità e alla velocità del fluido e alla lunghezza del tubo ed è inversamente proporzionale al quadrato del raggio della sezione. Ad ogni metro di tubo corrisponde quindi una certa perdita di carico; inoltre, più il fluido scorre veloce, più energia viene dissipata.
Poiché le perdite di carico risultano proporzionali alla lunghezza del condotto, si considerano distribuite lungo il condotto stesso e per questo vengono definite perdite distribuite.

 

FATTORE DI ATTRITO

 

La perdita di carico può anche essere espressa in funzione del numero di Reynolds, la cui espressione è
,
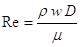in cui r è la densità del fluido e D il diametro della sezione del tubo.
Si consideri infatti la relazione (1): moltiplicandola e dividendola per la velocità media w, per la densità r e sostituendo il raggio R con il diametro D, si ottiene:
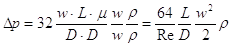                            (2)
L/D è un rapporto adimensionale e w2 /D è l’energia cinetica a meno del fattore a.
Il numero puro 64/Re prende il nome di fattore di attrito e viene indicato, a seconda dei testi, con le lettere f, x o l. Tali differenze nella nomenclatura dipendono dal fatto che il moto dei fluidi è un argomento al confine tra tre settori scientifici diversi: la fisica tecnica (disciplina appartenente alle scienze termiche), l’idraulica (disciplina appartenente all’ingegneria civile) e l’aerodinamica (disciplina appartenente all’ingegneria meccanica e aeronautica).
A volte, nella termofluidodinamica, viene  usato anche un altro fattore, Cf, pari a
.
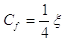In questa trattazione, seguendo la scuola tradizionale della fisica tecnica, si utilizzerà il fattore di attrito e lo si indicherà con la lettera x. L’espressione della perdita di carico risulta allora
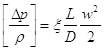                                                 (3)
Tale espressione non ha però validità generale: è esatta solo nel caso particolare di regime laminare completamente sviluppato, con tubo di sezione circolare e superficie liscia, quando cioè è valida la soluzione parabolica di Poiseuille. Il fattore di attrito non è una costante: in tutti gli altri casi x assume un valore diverso da 64/Re.. Il fattore di attrito è definito come quel numero puro che rende vera la relazione (3) e il suo valore, che viene ricavato sperimentalmente, dipende principalmente da tre fattori:

• il numero di Reynolds.
• la rugosità relativa: è un fattore che si potrebbe definire di forma e che dipende dalla possibilità che le pareti del tubo siano non lisce ma rugose. Si indica con il rapporto adimensionale e/D, dove e è la rugosità, definita come l’altezza media delle asperità in millimetri sulla superficie della parete, e D il diametro in millimetri del tubo.
• un parametro che dipende dalla distanza x dal punto di imbocco del tubo ed è pari a x/D. La dipendenza da questo termine viene in genere trascurata. Infatti le perdite di carico sono funzione di x solo nella regione di ingresso del tubo, in quanto la velocità è funzione di x; tale dipendenza invece scompare  nel regime sviluppato che, nel  caso più frequente di regime turbolento, si instaura dopo solo 10 diametri.

 

DIAGRAMMA DI MOODY

 

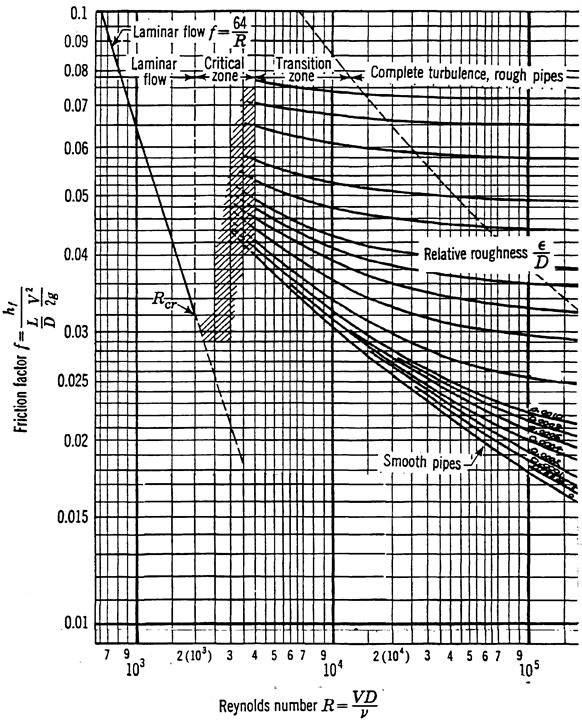
I valori del fattore di attrito inteso come funzione del numero di Reynolds e della rugosità relativa sono tabulati. Questa funzione viene anche rappresentata graficamente tramite un diagramma. Tale diagramma venne realizzato pressoché contemporaneamente da studiosi di fluidodinamica, di idraulica e di aerodinamica ed è conosciuto come diagramma di Moody (fig. 1) o, in idraulica, arpa di Nikuradse, per la forma caratteristica.
Il diagramma, che è realizzato in scala doppio logaritmica, riporta in ascissa il numero di Reynolds e in ordinata il fattore di attrito.
Nelle ipotesi di regime laminare completamente sviluppato con tubo di sezione circolare e superficie liscia la curva è un’iperbole equilatera.
Nel caso generale si suddivide il diagramma in tre zone distinte.

• La prima zona è caratterizzata dal regime laminare e si estende fino a Re = 2300. In tale regione la curva è una retta con pendenza negativa. 
• La seconda zona è zona di transizione: qui il diagramma non viene disegnato perché non se ne conosce l’andamento.
• La terza zona, che ha inizio per Re = 4000 - 4100, è caratterizzata dal regime turbolento. In questo caso la curva parte da un alto valore di fattore di attrito e decresce. Se il tubo è liscio la curva decresce indefinitamente; se invece il tubo presenta una certa rugosità la curva assume un andamento simile a quello di una retta parallela all’asse delle ascisse in corrispondenza di un certo numero di Reynolds. Il valore di tale numero di Reynolds diminuisce con l’aumentare della scabrosità del tubo, che nel diagramma è riportata su un asse verticale a destra, ma è comunque molto elevato, dell’ordine di 105, 106 (per avere valori così elevati del numero di Reynolds si devono normalmente utilizzare tubi con diametri molto grandi).

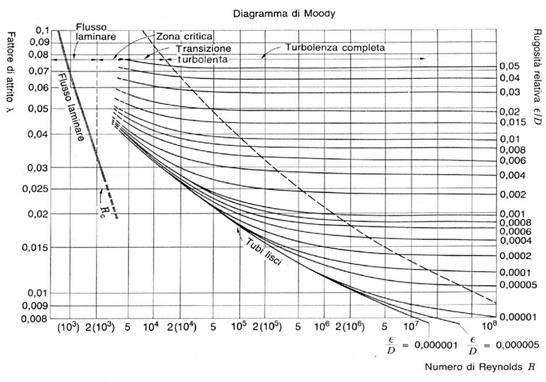
(fig. 1)

(tab. 1)

Al diagramma di Moody viene generalmente allegata una tabella (tab. 1) che riporta i valori della scabrezza per i materiali con cui tipicamente si realizzano i tubi per il trasporto dell’acqua.
Ad eccezione del tratto in cui la curva assume l’andamento simile a quello di una retta orizzontale, in cui vale la relazione
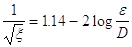                                          (4)
il diagramma di Moody non consente di risolvere i problemi in forma chiusa. Il fattore di attrito infatti è noto solo se è noto il numero di Reynolds. Ma se il numero di Reynolds è un’incognita, cioè il problema è a velocità non assegnata, si deve procedere nella risoluzione per tentativi. Si ipotizza una velocità, che viene detta di tentativo, si determina mediante il diagramma di Moody il fattore di attrito corrispondente e si ricava in funzione di esso, mediante l’equazione (3), una nuova velocità, sicuramente diversa da quella di tentativo. A partire dalla nuova velocità si ripetono le stesse operazione iterativamente finché il risultato non si stabilizza.
I risultati ottenuti vengono utilizzati nella pratica per risolvere diversi tipi di problemi.

PROBLEMA
Si calcoli la perdita di carico di un tubo (fig. 2) avente un diametro interno D di 2 in, una lunghezza L di 75 ft, nel quale scorre ammoniaca (NH3) satura alla temperatura T di 10 °F e con una velocità media w di 70 ft.s-1. La scabrezza e del condotto sia pari a 0.00015 ft, la viscosità dell’ammoniaca m 5.78 10-6 lb.ft-1s-1 e la sua densità r 0.137 lb.ft3.

(fig. 2)
Soluzione

Convertendo i dati nel sistema internazionale, considerando che
1 in = 2.540 × 10-2 m
1 ft = 0.3048 m
1 lb = 0.4536 kg
1 lb.ft-3 = 16.02 kg.m-3
e che la relazione tra le scale Celsius (C) e Fahrenheit (F) è
TF = 9/5 TC + 32
si ottengono i seguenti dati:
D = 50.8 mm
L = 22.86 m
T = -12.2 °C
w = 21.3 m.s-1
e = 0.046 mm
m = 8.6 × 10-6 kg.m-1×s-1 =  8.6 × 10-6 Pa×s
r = 2.19 kg.m-3
Per calcolare la perdita di carico nel tubo si usa la relazione (3):
.
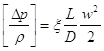Il valore del coefficiente di attrito x è funzione del numero di Reynolds Re e della rugosità relativa e/D.

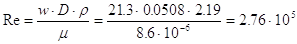
Tale valore di Re è piuttosto elevato e pertanto il regime sarà fortemente turbolento.

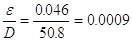
Con questi valori si può leggere sul diagramma di Moody che il fattore di attrito x è:
x = 0.0205
Dalla (3) si ricava allora che

 

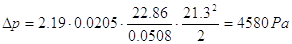
Nell’esercizio precedente la perdita di carico è stata espressa in Pascal poiché sono state usate le unità di misura del sistema internazionale. Ma in idraulica tradizionalmente le perdite di carico vengono espresse in metri di colonna d’acqua. Infatti tale scienza definisce il carico come la grandezza fisica che esprime, in metri di colonna d’acqua, la pressione esercitata dall’acqua stessa.
Per convertire i metri di colonna d’acqua in Pascal, e cioè per passare da una misura lineare in altezza alla corrispondente misura di pressione, si utilizza la legge di Stevino. Secondo tale legge, che regola la statica dei fluidi e cioè è valida se il fluido è in equilibrio, se si considera la pressione agente sul pelo libero nulla, la pressione a una quota generica del fluido x è  p = r×g×x, in cui g è l’accelerazione di gravità.
Se per esempio si considera l’acqua, che ha una densità r di 1000 kg.m-3, approssimando l’accelerazione di gravità g a 10 m.s-2 (vale 9.81 m.s-2), si ottiene la relazione 1 bar = 10 m, che è assolutamente scorretta in termini dimensionali, ma in idraulica viene assunta come equivalenza.
Non si deve però cadere nell’errore di considerare carico e pressione equivalenti quando il fluido è in moto. Si esamini infatti il seguente problema.
PROBLEMA
Dato un serbatoio contenente acqua dotato di un tubo da cui l’acqua fuoriesce (fig. 3), si determini la pressione nel punto 2 in cui il tubo termina, considerando che questo si trova ad una distanza H di 20 metri dal pelo libero dell’acqua.

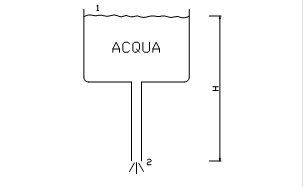
(fig. 3)
Soluzione
Poiché l’acqua è in moto non si può applicare la legge di Stevino e concludere che la pressione in 2 è
p2 = r×g×H = 2 bar.
Nonostante il dislivello, la pressione in 2 è uguale alla pressione in 1: la differenza di pressione è nulla perché è stata assorbita dalle perdite di carico.
Bisogna quindi semplicemente concludere che la pressione in 2 è, come in 1, la pressione atmosferica, che in idraulica, aerodinamica e fluidodinamica si assume pari a zero. Quindi
p1 = 0, p2 = 0.
In realtà la pressione atmosferica è pari a 1 bar, ma queste scienze, basandosi sul fatto che è sempre presente, la considerano inesistente, cioè nulla, e riportano ad essa le altre pressioni che per questo vengono dette relative. I manometri sono volutamente tarati perché la misura della pressione atmosferica sia zero. Tale ragionamento non è però pienamente giustificabile in quanto la pressione atmosferica non è una costante fisica, ma varia, ad esempio al variare dell’altitudine (in montagna la pressione atmosferica è significativamente più bassa di quella che si ha al livello del mare).

 

PERDITE DI CARICO CONCENTRATE

Le perdite di carico distribuite non sono le uniche cause di cadute di pressione nei condotti idraulici. Esistono infatti anche le perdite di carico dette concentrate o localizzate. Esse sono dovute agli ostacoli come, ad esempio curve, gomiti, valvole, brusche variazioni di pressione, che il fluido può incontrare mentre scorre all’interno del tubo. La figura seguente (fig. 4) mostra alcune tipiche cause di perdite di carico concentrate.
Sono schematizzati uno spigolo vivo ed una curva ben raccordata (che danno una perdita di carico diversa), un rubinetto (la perdita di carico dipende da quanto il rubinetto è aperto ed è comunque non nulla anche se questo è completamente aperto), una diramazione che termina con un rubinetto (c’è perdita di carico anche se il rubinetto è chiuso), un tubo la cui sezione si allarga in un caso e si restringe nell’altro in modo brusco e dolce.


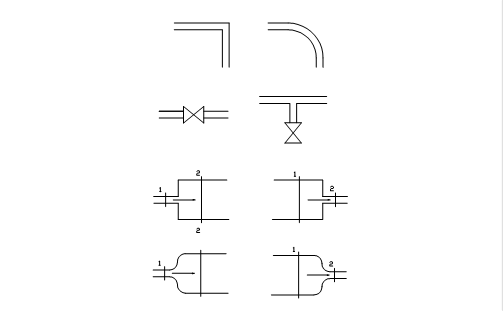
(fig. 4)
Le perdite di carico concentrate hanno un’espressione coerente con quella delle perdite di carico distribuite. Ma a differenza di queste ultime, le perdite di carico concentrate non dipendono dalla lunghezza del tubo (scompare il termine L/D), in quanto sono localizzate (concentrate) in un ben determinato punto. Indicando con b il fattore di attrito, l’espressione delle perdite di carico concentrate è:
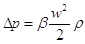                                                      (5)
in cui w e r sono rispettivamente la velocità media e la densità del fluido. E’ necessario però prestare attenzione alla velocità che si considera. Infatti se la sezione del tubo ha diametro costante anche la velocità è costante, ma se il diametro varia, come negli ultimi casi della figura 4, la velocità in ingresso w1 è diversa da quella in uscita w2. Per l’equazione di continuità introdotta nello studio dei sistemi aperti in regime stazionario la portata in massa che entra nella sezione 1 è uguale alla portata in massa che esce dalla sezione 2, e cioè

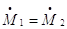
Ma poiché questa relazione si può scrivere anche nella forma
r w1 S1 = r w2 S2
dove S è la sezione del tubo, si deduce subito che se la sezione si allarga la velocità diminuisce, mentre se la sezione si restringe la velocità aumenta.
Tutto ciò è valido se si ipotizza la densità r del fluido costante. Infatti la relazione di proporzionalità diretta tra velocità del fluido e sezione del tubo può non essere valida se si considera che al variare della pressione può variare anche il volume specifico del fluido e quindi la sua densità. Considerare r costante è nella maggior pare dei casi un’approssimazione ragionevole (per esempio si può considerare costante la densità dell’aria che circola nei tubi di un impianto di ventilazione, in cui la variazione di pressione complessiva è trascurabile rispetto la pressione atmosferica, mentre non si può considerare costante la densità di un gas che, passando attraverso un ugello, viene portato dalla pressione di 1 bar a quella di 50 bar).

 

 
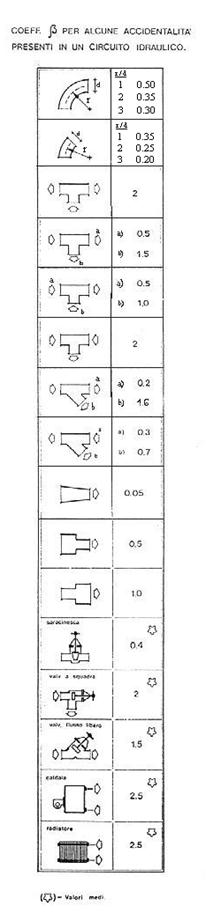
(fig. 6)
I valori del fattore di attrito b per i casi più comuni sono riportati in tabelle. Nella  tabella di figura 6 si può ad esempio leggere che b può variare tra 0.3 e 0.5 in una curva a gomito ben raccordata, vale 2 per una diramazione a T, 0.5 se il tubo si allarga e 1.5 se il tubo si restringe (diversamente da quanto si potrebbe pensare si ha una perdita maggiore allargando il tubo piuttosto che strozzandolo), vale 0.4 per una valvola a saracinesca, 2 per una valvola a squadra aperta, 2.5 per una caldaia. Si può così ad esempio determinare la pompa che occorre per mantenere in circolazione l’acqua in un impianto di riscaldamento. Infatti la somma delle perdite di carico distribuite e concentrate in tutto l’impianto deve essere bilanciata dal salto di pressione prodotto dalla pompa: in un impianto di 300-500 metri in cui le perdite di carico sono pari a 4.5 bar sarà necessaria una pompa da 5 bar.

 

DIAMETRO EQUIVALENTE

L’espressione delle perdite di carico distribuite (3) non è corretta se si considerano tubi di sezione non circolare. Se la sezione del tubo non è circolare nella relazione (3) si deve sostituire il diametro D con il cosiddetto diametro idraulico equivalente (DEQ), che viene definito

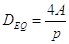
con A e p pari rispettivamente all’area ed al perimetro della sezione.

 

Si considerino le sezioni in figura 7.

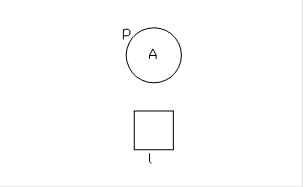
(fig. 7)
Nel caso di tubo a sezione circolare si ha


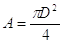
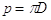
e quindi, come deve essere,
.
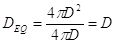Ma nel caso di tubo a sezione quadrata di lato l si ha


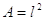
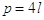
e quindi
.
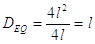Ma il calcolo del diametro equivalente non è sempre così semplice. Esistono per questo tabelle (tab. 2) che riportano il valore del diametro equivalente di tubi con sezione particolare. La tabella 2 riporta inoltre il numero da sostituire a 64 nell’espressione per il calcolo del fattore di attrito x=64/Re a seconda della forma della sezione del tubo. Il fattore di attrito ad esempio è x=57/Re per un tubo di sezione quadrata (è un valore non molto diverso da x=64/Re, se si considera che gli errori che si commettono in questo regime di moto dei fluidi sono normalmente del 30%) , x=53/Re per un tubo di sezione triangolare, x=96/Re per un tubo di sezione anulare.

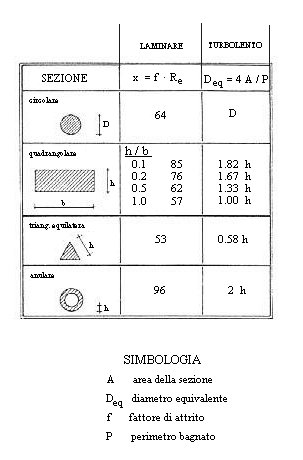
(tab. 2)

 

LUNGHEZZA EQUIVALENTE

Per calcolare la perdita di carico totale, anziché sommare alle perdite di carico distribuite le perdite di carico concentrate, si può procedere con un metodo alternativo. Questo consiste nell’utilizzare direttamente la formula (3), con la sola accortezza di maggiorare la lunghezza del condotto sostituendo L con L+LEQ , dove LEQ è la somma delle lunghezze equivalenti di tutte le accidentalità.
Per determinare una lunghezza equivalente si usa un nomogramma (fig. 8).

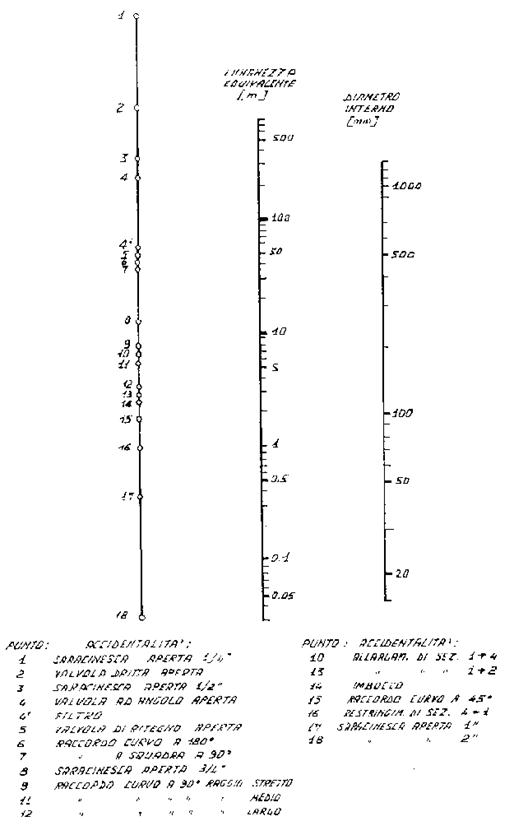
(fig. 8)

Tale diagramma è costituito da tre assi verticali paralleli: su quello a destra vengono riportati i valori del diametro interno della sezione del tubo in millimetri,  su quello a sinistra valori corrispondenti alle accidentalità del tubo e su quello centrale i valori della lunghezza equivalente in metri. Conoscendo il diametro interno del tubo e il tipo di accidentalità si può ricavare il valore della lunghezza equivalente semplicemente congiungendo con una retta i due punti sugli assi esterni corrispondenti ai valori noti: la lunghezza equivalente è pari al valore in metri corrispondente al punto in cui tale retta interseca l’asse centrale.     
Per esempio la lunghezza equivalente di un tubo avente diametro interno pari a 100 mm con una valvola ad angolo aperta (corrisponde al punto 4) è circa 20 m, mentre la lunghezza equivalente di un tubo dello stesso diametro interno che ha un restringimento di sezione da 4 ad 1 (punto 16) è poco più di 1 m.

 

Fonte: http://pcfarina.eng.unipr.it/dispense99/patini119156.doc

Autore del testo: Clara Patini

 

 

Le perdite di carico

 

Verranno trattati i seguenti argomenti:

• Perdite di carico distribuite e concentrate;

• Fattori d’attrito;

• Utilizzo del diagramma di Moody;

• Diametro equivalente;

• Un’applicazione dell’equazione di Navier: l’equazione di Bernoulli.

 

Un fluido che scorre dentro una tubazione è soggetto alle cosiddette perdite di carico, ovvero ad un calo di pressione dovuto agli attriti interni dello stesso: il nostro scopo è riuscire a calcolarle, anche se in maniera approssimata. È importante osservare che le leggi che regolano il moto di un fluido non sono, purtroppo, universalmente valide: il modo stesso con cui questo si muove varia in funzione della sua velocità, della viscosità e della densità che lo caratterizzano, e del diametro del tubo entro cui esso fluisce. Per questo si è soliti ricorrere a due modelli per descrivere un fluido in moto: il regime laminare e quello turbolento; il primo prevede che questo sia suddivisibile in tante lamelle che scorrono (non senza attrito) una sull’altra e parallelamente al tubo; il secondo, invece, si basa sull’idea che le varie molecole si muovano in modo caotico, formando vortici. Si sceglie un modello o l’altro a seconda del valore di un parametro, il numero di Reynolds, definito da:

 

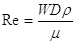
dove D è il diametro del tubo, W la velocità media del fluido, ρ la sua densità e μ la sua viscosità. A seconda del valore di tale parametro, dunque, si usa un modello, piuttosto che l’altro, sapendo che siamo in:

• Regime laminare                         se Re<2.100
• Regime turbolento                      se Re>4.000

 

Evidentemente, esiste un range entro il quale non vale nessuno dei due modelli: questo viene chiamato zona di transizione.
Possiamo ora prendere in esame le perdite di carico, osservando che vengono a loro volta suddivise in due categorie: quelle distribuite e quelle concentrate. Le prime sono dovute agli attriti che inevitabilmente si generano a causa dello scorrere del fluido nel tubo, perciò sono presenti (distribuite) ovunque nelle tubazioni; le perdite concentrate, al contrario, sono localizzate in un ben preciso punto del percorso, e sono dovute ad ostacoli quali un rubinetto, una diramazione, un restringimento o un allargamento del condotto, un gomito ecc.
Ora che abbiamo definito ciò che vogliamo trattare, possiamo fare un primo calcolo di perdita di carico: per esempio, quella distribuita dovuta ad un tubo rettilineo di sezione circolare di raggio R, e lunghezza L, perfettamente liscio, entro

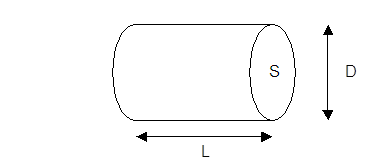
cui scorre un fluido di viscosità μ in regime laminare: è già stata calcolata
l’espressione della velocità in funzione della caduta di pressione 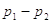 tra due sezioni 1 e 2:

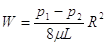
Risolvendo tale equazione rispetto alla caduta di pressione, ed esprimendo il raggio in funzione del diametro, si ottiene:

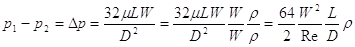
da cui:

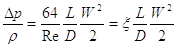                               (1)

Il termine 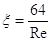 è chiamato coefficiente d’attrito, e tale espressione vale solamente sotto le ipotesi che abbiamo fatto, in particolare quelle di tubo liscio, sezione circolare e moto laminare. È anche da notare come l’espressione appena ricavata per la perdita di pressione sia direttamente proporzionale al termine , quindi alla lunghezza relativa del tubo: questo fattore esprime il concetto dei perdita distribuita.
Qualora non valessero le ipotesi sotto le quali abbiamo sviluppato il calcolo, possiamo comunque utilizzare la formula (1) ricavando il coefficiente d’attrito non più per via analitica, ma mediante l’uso di tabelle o del diagramma di Moody, di origine sperimentale, in funzione del numero di Reynolds e della rugosità relativa, 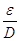, dove D è sempre il diametro del tubo, mentre ε è il valore medio della sua scabrezza (solitamente, entrambi sono espressi in mm).
Osserviamo dunque il diagramma di Moody, che si presenta sotto forma di retta nel caso di regime laminare, in cui vale la relazione:

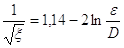
Aumentando il valore di Re, si entra nel regime turbolento, e il diagramma si divide in più curve, ognuna delle quali rappresenta un particolare valore della scabrezza relativa (relative roughness, nel grafico); la curva inferiore si riferisce al caso del tubo liscio (smooth pipe). Il grafico si usa scegliendo la curva corrispondente alla scabrezza del tubo in esame e individuando su di essa il punto la cui ascissa rappresenta il numero di Reynolds del problema: sull’indice di sinistra si può leggere il valore di ξ. Si noti che la zona critica e quella di transizione non sono trattate: il grafico diventa tratteggiato, e poi subisce una discontinuità; si osservi, infine, che le curve del regime turbolento tendono a spianare all’aumentare del numero di Reynolds.

Abbiamo in precedenza accennato alle perdite di carico concentrate: ci poniamo ora l’obiettivo di trovare una formula per calcolarle, formula che – in linea di massima – non dovrebbe essere troppo diversa da quella già vista per le perdite distribuite; è perciò naturale aspettarsi che il rapporto tra la perdita di pressione e la densità del fluido sia direttamente proporzionale all’energia cinetica del fluido stesso mediante una costante, che è solitamente indicata dalla lettera β; inoltre, dovrà scomparire il termine 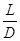, che esprimeva il concetto di perdita distribuita. In effetti, la formula usata per calcolare le perdite di carico concentrate è:

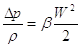
Il termine β, che mantiene il nome di coefficiente d’attrito, dipende dalla particolare geometria dell’oggetto che determina la perdita, ed è tabulato; seguono i valori trovati per alcuni snodi.

In alternativa al metodo appena illustrato, esiste anche uno speciale diagramma costituito da tre linee parallele: sulla prima sono indicati alcuni indici, ognuno dei quali rappresenta un elemento di perdita concentrata; sull’ultima è invece presente una scala di lunghezze che indica il diametro interno del tubo: congiungendo con un segmento i due punti che individuano il problema, questo intercetta sulla linea centrale un particolare valore espresso in metri, che prende il nome di lunghezza equivalente: si tratta della lunghezza che un tubo deve avere per generare la stessa perdita di carico dovuta all’elemento che stiamo analizzando. Perciò è possibile trovare le lunghezze equivalenti di tutti gli elementi che generano perdite di carico localizzate, e calcolare la perdita totale considerando solo quelle distribuite dovute ad un percorso allungato ad hoc.
Come si può vedere dalla tabella, anche un restringimento della tubazione è fonte di perdita di carico, e lo stesso vale per un allargamento; il coefficiente da usare dipende in questo caso sia dalla variazione di diametro, sia da quanto bruscamente questa avviene. Se cambia il diametro, anche la velocità del fluido si adegua, e, più precisamente, aumenta se il diametro si restringe, e viceversa. Ciò deriva dal considerare che la portata in massa delle tubazioni deve rimanere costante in ogni punto, quindi anche nelle sezioni 1 e 2 in figura:

Possiamo esprimere tali portate nel solito modo:

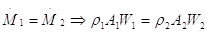
Se il fluido che trattiamo è un liquido, si può considerare costante la densità che, quindi, si semplifica:

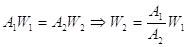
quindi, se diminuisce la sezione, aumenta la velocità.
Fino ad ora abbiamo affrontato il calcolo delle perdite di carico dapprima in un caso semplice (tubo liscio, sezione circolare, moto laminare), poi abbiamo via via rimosso le semplificazioni per portare la nostra trattazione ad un caso sempre più generale: in quest’ottica, l’ultimo passo che ci manca è quello di considerare la sezione non più circolare, ma di forma qualsiasi. Infatti, è a volte utile o necessario utilizzare tubi di sezione particolare, come quella quadrata, quella triangolare ecc., nel qual caso la teoria finora sviluppata non funziona in maniera efficiente; è però possibile modificare un parametro per sfruttarla di nuovo. Allo scopo, introduciamo il concetto di diametro equivalente: con questo, è possibile trattare i tubi di qualsiasi sezione come se questa fosse circolare, ed utilizzare quindi tutte le formule viste finora; esso è definito come il rapporto tra il quadruplo dell’area della sezione e il perimetro bagnato, ovvero quello “visto” dal fluido:

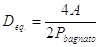
Evidentemente, per tubi di sezione circolare il diametro reale e quello equivalente coincidono; proviamo poi a fare il calcolo in casi semplici:

 

• Sezione quadrata:

Detto L il lato del quadrato, il diametro equivalente è dato da:

 

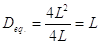
• Sezione triangolare:

Considereremo il caso più semplice: triangolo equilatero:

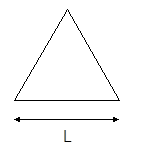
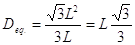
• Sezione ad anello:

 

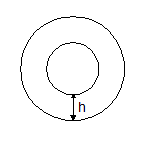
In questo caso è segnato sul disegno solamente il passo h tra il tubo interno e quello esterno, poiché è l’unico parametro in funzione del quale si esprime il diametro equivalente; infatti, se R e r sono, rispettivamente, il diametro del tubo esterno e quello del tubo interno, si può scrivere:

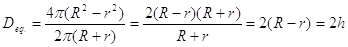
Una volta spiegato come calcolare le perdite cui un fluido va incontro scorrendo nei tubi ed attraversando gli ostacoli che eventualmente incontra, è ora facile fare l’analisi di un sistema nel suo complesso, dato che questo è scomponibile negli elementi semplici che sappiamo gestire: dovendo, quindi, scegliere una pompa per mantenere un certo flusso dentro un sistema, questa deve generare una differenza di pressione superiore alla perdita di carico totale, data da:

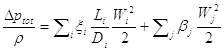
Proviamo a mettere in pratica quello che è stato illustrato.

 

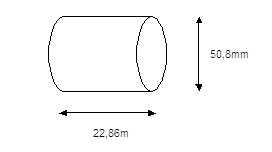
Problema.

Si calcoli la perdita di carico dovuta ad un tubo di diametro D=50,8mm e lunghezza L=22,86m, con una rugosità media m, se vi scorre ammoniaca alla temperatura di –12,2°C alla velocità di .

Risoluzione.

L’ammoniaca ha viscosità 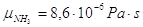 e densità .
Una volta scoperti questi dati dalle tabelle, è possibile risolvere il problema. La prima cosa da fare è scoprire se siamo in regime laminare o turbolento, visto che il procedimento risolutivo, come già osservato, dipende fortemente da questa constatazione; calcoliamo dunque il numero di Reynolds:

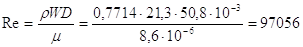
Il regime è dunque fortemente turbolento.
Calcoliamo poi la scabrosità relativa:

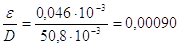
Avendo ora Re e la scabrosità, è possibile, grazie al diagramma di Moody, determinare il coefficiente d’attrito: risulta 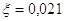. Il passo finale è, ovviamente, il calcolo della perdita di carico distribuita:

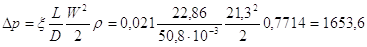Pa

 

Dall’equazione di Navier a quella di Bernoulli.

Lo studio della fluidodinamica si basa su un’equazione che ne costituisce la base: l’equazione di Navier, già enunciata in altri contesti, e che qui ricordiamo:

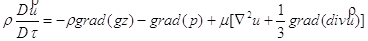
Quest’equazione rappresenta l’andamento della derivata sostanziale della velocità in funzione della forza di gravità (primo termine), e di quella dovuta alle pressioni (secondo termine), le quali costituiscono il “motore” del fluido, ovvero le cause che tendono a muoverlo; poi, viene contemplato l’ultimo termine, che rappresenta gli impedimenti che ostacolano il moto del fluido stesso. Grazie ad essa è possibile, analizzando le condizioni al contorno del fluido, dedurre il vettore velocità in funzione delle tre coordinate spaziali e di quella temporale: 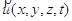. Purtroppo, anche se questa equazione ha validità generale, e – almeno in linea teorica – potrebbe risolvere in maniera accurata i problemi della fluidodinamica, la sua espressione è evidentemente molto complessa, quindi non viene di fatto usata nei calcoli per le situazioni reali. È però possibile ricavare da questa espressione la ben nota (e usata) equazione di Bernoulli, che è già stata utilizzata in altri ambiti per la risoluzione pratica di alcuni problemi. Prendiamo quindi in considerazione un tubo di flusso: esso è un tubo ideale che non può essere attraversato dal fluido se non dalle sezioni di ingrasso e di uscita; in altre parole, la sua superficie laterale è “impermeabile”. Di primo acchito potrebbe sembrare un concetto strano, ma basta pensarlo come il tubo generato da tutte le linee di flusso che passano per una curva chiusa, che determina così una delle due sezioni; l’altra è individuata da un’ulteriore linea chiusa che intercetta le medesime linee di flusso. Risulta ora più naturale pensare che la superficie laterale del nostro tubo ideale sia impermeabile: le linee di flusso non si incrociano mai; naturalmente, nulla garantisce che le due sezioni siano uguali, e infatti generalmente non lo sono. Infine, osserviamo che non è possibile sfruttare l’ipotesi dell’aderenza, poiché le pareti di un tubo di flusso non esistono.

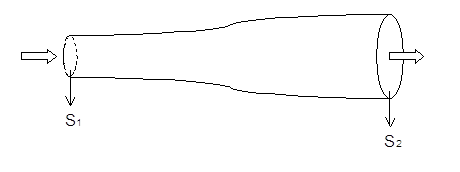
Ipotizziamo che il nostro sistema si trovi in regime stazionario: ciò porta a considerare nulle tutte le derivate temporali, e a porre uguali il flusso entrante e quello uscente; integriamo poi l’equazione di Navier, facendo in tal modo un bilancio dell’energia. Il calcolo è assai complesso, e viene perciò omesso; il risultato è:

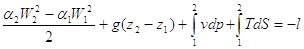
dove i coefficienti 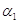 e , che tengono conto dei profili di velocità, vengono generalmente posti uguali a 1, considerando la velocità stessa uniforme sulle sezioni; si noti inoltre come siano stati considerati volume e lavoro specifici. Il termine  prende il nome di energia meccanica specifica, ed esprime una sorta di resistenza idraulica: quella che oppone il fluido allo scorrimento, a causa della propria viscosità, ed è a volte indicata con la lettera R; z1 e z2 sono invece le quote delle due sezioni: non è detto che il tubo sia orizzontale. Tentiamo ora di sviluppare ulteriormente, assumendo unitarie le costanti di cui abbiamo parlato; per prima cosa cerchiamo dunque di eliminare i due integrali, che tendono a far aumentare la complessità dei calcoli, osservando che, per definizione:

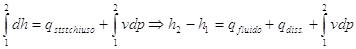
avendo indicato con qsist. chiuso la somma del calore del fluido e di quello dovuto ai fenomeni dissipativi. Ricordando che il volume specifico è l’inverso della densità:

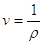
possiamo eliminare l’integrale che era rimasto:

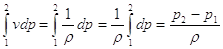
Riusciamo dunque a scrivere l’equazione di Bernoulli, priva di integrali:

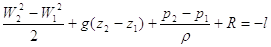
Mettiamo in luce, da ultimo, che il termine R non è altro che l’insieme delle perdite di carico che abbiamo formalizzato all’inizio della trattazione, il che è naturale, visto che deve esprimere la resistenza che il fluido oppone allo scorrimento. Perciò è possibile esplicitare R come segue:

 

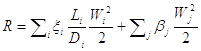
fonte: http://pcfarina.eng.unipr.it/dispense00/ghidoni125948.doc

autore: Stefano Ghidoni

 

 

Perdite di carico

 

 

Perdite di carico

 

Disclaimer

Questo sito non rappresenta una testata giornalistica e viene aggiornato senza alcuna periodicità, esclusivamente sulla base della disponibilità del materiale, pertanto non è un prodotto editoriale sottoposto alla disciplina di cui all'art. 1, comma III della Legge n. 62 del 7.03.2001. I riassunti , gli appunti i testi e le citazioni contenuti nel nostro sito sono messi a disposizione gratuitamente a studenti, ricercatori, professori, tecnici con scopi illustrativi didattici e scientifici con il concetto del fair use e con obiettivo del rispetto della direttiva europea 2001/29/CE e della legge n. 633 art. 70 e dlg 68. Il sito è curato e coordinato dall’autore al solo scopo informativo e didattico. Pur ritenendo le fonti utilizzate affidabili, l'autore di questo sito non garantisce l'accuratezza e l'integrità delle informazioni contenute e pertanto declina ogni responsabilità per eventuali problemi o danni causati da errori o omissioni, nel caso tali errori o omissioni risultino da negligenza, caso fortuito o altra causa. Tutti gli appunti, le citazioni i testi e le immagini , sono proprietà dei rispettivi autori o case di produzione che ne detengono i diritti, qualora gli aventi diritto si ritenessero danneggiati dall'inserimento in questo sito dei predetti files o fossero stati inavvertitamente inseriti immagini, informazioni, testi od altro materiale coperto da Copyright saranno immediatamente rimossi e/o ne saranno citate le fonti su semplice segnalazione all' indirizzo e-mail indicato nella pagina contatti .

Gli obiettivi di questo sito sono il progresso delle scienze e delle arti utili in quanto pensiamo che siano molto importanti per il nostro paese i benefici sociali e culturali della libera diffusione di informazioni utili. Tutte le informazioni e le immagini contenute in questo sito vengono qui utilizzate esclusivamente a scopi didattici, conoscitivi e divulgativi. Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione). In questo sito abbiamo fatto ogni sforzo per garantire l'accuratezza dei tools, calcolatori e delle informazioni, non possiamo dare una garanzia o essere ritenuti responsabili per eventuali errori che sono stati fatti, i testi utilizzati sono stati prelevati da siti che li hanno messi a disposizione gratuitamente per farli conoscere nel web con scopi didattici. Se trovate un errore su questo sito o se trovate un testo o tool che possa violare le leggi vigenti in materia di diritti di autore, comunicatecelo via e-mail e noi provvederemo tempestivamente a rimuoverlo.

 

---

 

---

 

Designed by Larapedia.com 1998 -2011