Matematica riassunti

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Matematica riassunti

Riassunto Matematica

Una disequazione è lineare se è di primo grado. Le disequazioni lineari in due incognite possono essere ricondotte alla forma ax+by+c>0 o analoghe. Per risolverle si rappresenta sul piano la retta e si individua la parte di semipiano contenente le soluzioni. Le disequazioni non lineari si risolvono come quelle lineari. Per i sistemi di disequazioni in due variabili, bisogna determinare l’intersezione fra le soluzioni di ogni disequazione.

L’equazione esplicita dello spazio è: z=mx+ny+q. m e n rappresentano i parametri direttori del piano tangente ad un punto. La forma implicita è ax+by+cz+d=0. La z rappresenta la quota, la y l’ordinata e la x l’ascissa. Tra le superfici particolari troviamo:

Elissoide:
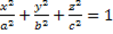
Iperbole a una falda:
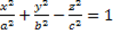
Iperbole a due falde:
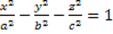
Paraboloide elittico:
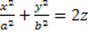
Paraboloide iperbolico:

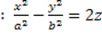
Una funzione è una relazione che associa ad ogni elemento di D (dominio) uno e un solo elemento di C (codominio). Si dice funzione reali di due variabili reali una relazione che associa a ogni coppia ordinata di numeri reali (x;y), appartenente a un sottoinsieme S (dominio) di RxR, uno e un solo numero reale z (codominio). Il campo di esistenza di una funzione di due variabili z= f(x;y) è l’insieme di tutte le coppie (x;y) appartenenti a RxR per le quali la funzione è definita.

Per la rappresentazione di funzioni di due variabili si può utilizzare il metodo dei grafici per punti o le linee di livello. Una linea di livello è l’insieme delle proiezioni ortogonali sul piano oxy dei punti di una superficie che hanno tutti la stessa quota z=k.

Si chiama derivata parziale della funzione z=f(x;y) rispetto a x nel punto P₀(x₀;y₀) il limite, se esiste finito, per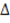

Si chiama derivata parziale della funzione z=f(x;y) rispetto a y nel punto P₀(x₀;y₀)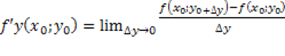

L’equazione del piano tangente a P(x₁;y₁;z₁) è: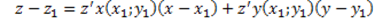

Se le derivate parziali prime sono funzioni derivabili, si possono definire le derivate parziali seconde. Le derivate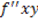

Si ha un punto di massimo relativo P₀(x₀;y₀) di una funzione z=f(x;y) se per tutti i punti di un intorno di P₀ 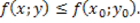. I punti di massimo e minimo vengono detti punti estremante della funzione.

Secondo il teorema di Weierstrass, se una funzione z=f(x;y) è continua in un insieme limitato e chiuso D, è dotata di massimo assoluto e di minimo assoluto in D.

La condizione necessaria perché una funzione z=f(x;y) abbia un punto di massimo o di minimo in un punto P₀(x₀;y₀) del suo dominio D è che le derivate parziali rispetto a x e y siano contemporaneamente nulle in P₀:

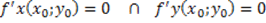
I punti trovati da questo sistema sono detti punti stazionari o critici.

Un punto è detto di sella se non è un punto di massimo o di minimo relativo.

Data la funzione z=f(x;y) definita in un insieme D contenuto RxR, dotata di derivate parziali seconde in D, si dice determinante hessiano H di f in un punto P0(x0;y0) appartenente al D il determinante:

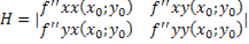
Secondo il teorema Hessiano, s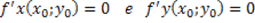e e:

Se H(x₀;y₀)>0 e 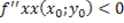, P è un punto di massimo relativo;
Se H(x₀;y₀)>0 e 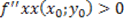, P è un punto di minimo relativo;
Se H(x₀;y₀)<0 P è un punto di sella;
Se H(x₀;y₀)=0, nulla si può dire a riguardo. Per scoprire la natura di P si utilizzano altri metodi.

In caso le variabili di una funzione non sono libere, ma sono vincolati, i valori estremanti della funzione vengono detti massimi e minimi vincolati. Questi per calcolarli si può ricorrere al metodo della sostituzione, il metodo delle linee di livello o il metodo di Lagrange.

Per risolvere con il metodo della sostituzione bisogna esplicitare una variabile del vincolo, sostituire la variabile alla funzione ottenendo una funzione ad una variabile. Ora si studia il segno della derivata prima.

Per risolvere con il metodo di Lagrange, bisogna prima creare una nuova funzione, la funzione lagrangiana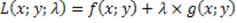

Poi trovare i punti critici tramite la condizione necessaria:

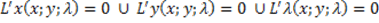
La condizione sufficiente per stabilire se i punti stazionari o critici sono massimi oppure minimi è espressa mediante l’hessiano orlato:

Ḣ=| |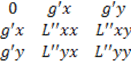

Se Ḣ(x₀;y₀;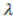₀) un minimo libero (e la funzione ammette un minimo vincolato in P₀).

Se Ḣ(x₀;y₀;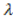₀)=0 non si può stabilire nulla.

Dati m e n numeri reali, si chiama matrice (numerica) del tipo (m,n) una tabella come quella degli hessiani. Gli elementi della matrice comprendono due indici, il primo rappresenta la linea orizzontale e l’altro la linea verticale. Per calcolare il determinante di una matrice del terzo ordine (come per l’hessiano ortolato), si può applicare il teorema di Sarrus. Si riscrivono a fianco della matrice le prime due colonne. Poi si calcola la somma dei prodotti degli elementi nelle diagonali primarie e la somma dei prodotti degli elementi nelle diagonali secondarie. Poi si sottraggono i valori ottenuti.

Ricerca Operativa

La ricerca operativa è una disciplina che fornisce gli elementi quantitativi di base necessari per le decisioni, relative alle operazioni controllate dal personale dirigente. Essa utilizza strumenti matematici per controllare nel modo più efficiente un sistema reale, cercando di studiarlo nel suo complesso.

La ricerca operativa ha iniziato a svilupparsi in ambito militare intorno al 1939, quando in Inghilterra si dovette risolvere il problema della difesa antiaerea dagli attacchi dei bombardieri tedeschi. Contemporaneamente, negli Stati Uniti, sorse il problema di difendere i convogli mercantili che dovevano approvvigionare le truppe operanti in Europa dagli attacchi dei sommergibili tedeschi. Non essendo sufficienti le strategie belliche, i militari si rivolsero a gruppi di scienziati con conoscenza e competenze diverse. I risultati di questo lavoro comune furono decisamente positivi e nacque così un nuovo modo di operare. Al termine del conflitto le conoscenze acquisite e le nuove metodologie furono rivolte alla ricostruzione, quindi al mondo dell’economia e dell’industria.

Le fasi della ricerca operativa sono:

Formulazione del problema, l’equipe di lavoro riceve informazioni generali. Deve quindi elaborarli, determinare con precisione gli obbiettivi da raggiungere, i vincoli che li limitano, le eventuali correlazioni con altre parti dell’insieme per cui si lavora;
Raccolta delle informazioni, la raccolta delle informazioni deve essere la più ampia e dettagliata possibile. Le informazioni vanno poi esaminate ed elaborate in modo da individuare le variabili del problema, i valori che possono assumere e le eventuali relazioni esistenti fra esse,
Costruzione del modello matematico, un modello matematico è un insieme di simboli ed espressioni matematiche che debbono rappresentare il problema in maniera chiara e precisa. Di solito un modello contiene una funzione obiettivo y=f(x₁,x₂,…,x_n), dove le variabili indipendenti sono variabili d’azione o variabili ammissibili; l’insieme dei valori che possono essere assunti dalle variabili viene detto regione o area ammissibile o campo di scelta, una relazione fra le variabili (vincoli tecnici) e vincoli di segno;
Risoluzione del modello, in questa fase si usano i metodi tradizionali della matematica. La soluzione ottima è un elemento della regione ammissibile che rende minima o massima la funzione obiettiva prefissata;
Controllo del modello e delle soluzioni ottenute, Si verifica se il modello teorico rappresenta abbastanza bene la realtà e si valuta se la soluzione ottimale ottenuta produce i benefici aspettati;

I problemi possono essere discreti quando le variabili d’azione possono assumere solo valori interi all’interno dei loro intervalli di variabilità, continui quando le variabili possono assumere tutti i valori nel loro intervallo di variabilità.

In base al numero di variabili vi possono essere problemi in una variabile o problemi in più variabili.

I problemi possono essere in condizione di certezza, in cui i dati sono sicuri e fissi, frutto di indagini precise, in condizioni di incertezza, in cui i dati dipendono da eventi casuali, che hanno una certa probabilità di verificarsi.

Esistono inoltre problemi con effetti immediati, se il tempo intercorrente fra la decisione e la realizzazione non influisce sulle grandezze economiche in questione; con effetti differiti, se invece bisogna valutare il tempo intercorrente fra la decisione e l’attuazione della scelta.

I costi fissi sono i costi che non dipendono dalla quantità x dei beni prodotti o venduti. I costi variabili sono i costi che dipendono dalla quantità x dei beni prodotti o venduti. Il ricavo è ciò che l’azienda ottiene dalla vendita dei beni R(x)= p*x. L’utile è la differenza tra i ricavi e i costi.

Se la funzione obiettivo è una retta, si può risolvere tramite il modello matematico o con il diagramma di redditività. Il diagramma di redditività è un grafico in cui sono evidenziate le relazioni fra spese fisse e spese variabili espressi da una funzione e dai ricavi espressi da un’altra funzione. Per risolvere attraverso il modello matematico, si trova l’intersezione con l’ascissa P(a;0). Per 0<=x<a si è in perdita, x=a guadagno nullo, per x>a guadagno. In caso di vincolo, il vincolo rappresenta il massimo guadagno.

Se la funzione obiettivo è una parabola, si rappresenta la parabola e si trovano le intersezioni con l’ascissa (guadagno nullo). Se, data la funzione y=ax²+bx+c, a>0, il guadagno massimo coincide con il vincolo (o, se non è presente, è infinito), altrimenti se a<0 il massimo guadagno si ha nel vertice V(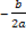). In questo caso se si ha un vincolo x<=k, si possono verificare due casi:

k<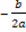, il massimo guadagno si ha in k;
k>;

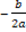Se la funzione obiettivo è un iperbole (funzione somma) y=a/x+bx+c, il costo unitario minimo si ottiene con la formula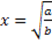

Se è espressa da più funzioni si rappresenta in un unico grafico le funzioni, si determinano le intersezioni e si individua quale funzione ha costi inferiori o guadagni superiori.

Il problema degli stock o delle scorte di magazzino riguarda i commercianti e tutti coloro che in qualche modo sono produttori di beni. Il bene deve essere presente nel magazzino in quantità ottimale se no si possono verificare delle rotture o delle sovrapposizioni. Le rotture si hanno quando vengono a mancare per un certo periodo di tempo delle materie, mentre le sovrapposizioni si hanno quando i rifornimenti arrivano prima dell’esaurimento delle scorte. I presupposti per risolvere questi problemi sono che non vi sia del tempo intercorrente tra un ordine e l’approvvigionamento delle merci e che il consumo sia uniforme.

Problemi di scorte di magazzino

I costi sono dati dalla somma tra i costi di ordinazione, quelli di magazzino e quelli di acquisto. (C=Cl+Cm+Ca). Cl è dato dal costo di ciascuna ordinazione per il rapporto tra la quantità totale e il lotto economico (Cl=co*M/Q). Cm è dato dai costi di magazzinaggio per la giacenza media (Cm=cm*Q/2). Il costo di acquisto è dato dal prodotto tra il prezzo di ogni merce per il totale del magazzino (Ca=p*M). Q rappresenta il lotto economico e per calcolarlo si applica la formula: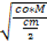

Per risolvere i problemi di programmazione lineare si individua la funzione obiettivo, si costruisce il sistema dei vincoli, si determinano le regioni ammissibili delle variabili e si individua il vettore H. poi si determina la retta guida z=0 e le linee di livello passanti per i vertici della regione ammissibile. Infine si individua le combinazioni massime e minime.

L’interpolazione è lo studio di un periodo attraverso il quale si può prevedere un evento futuro. È un metodo per individuare nuovi punti del piano cartesiano a partire da un insieme finito di punti dati, nell'ipotesi che tutti i punti si possano riferire ad una funzione f(x) di una data famiglia di funzioni di una variabile reale.

Si ha l’interpolazione per punti noti (o interpolazione matematica) se la funzione assume esattamente i valori rilevati e quindi il suo grafico passa per tutti i punti del diagramma di dispersione (diagramma che rappresenta le coppie ordinate di valori). Si ha l’interpolazione fra punti noti (o interpolazione statistica) se la funzione assume valori “vicini” ai valori rilevati e quindi il suo grafico passa fra i punti del diagramma di dispersione.

L’errore di accostamento è il segmento che manca affinché il punto appartenga alla funzione ed è dato dalla differenza tra i valori reali meno i valori teorici (errore parziale) e può essere negativo, nullo o positivo. L’errore totale (indicato con e) è dato dalla somma di tutti gli errori parziali.

La condizione di accostamento del metodo dei minimi quadrati consiste nel scegliere i valori numerici dei parametri in modo che risulti minima la funzione S somma dei quadrati degli errori relativi e_i: .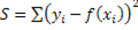

La condizione necessaria è che le derivate parziali rispetto ai parametri si annullino contemporaneamente.

L’errore standard è un indice di scostamento che determina quanto i valori teorici si avvicinano a quelli rilevati. L’errore standard è la radice quadrata della media della sommatoria del quadrato degli errori di accostamento: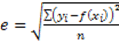

L’indice quadratico relativo può indicare un’interpolazione più o meno accettabile. È accettabile se I≤0,1. È dato dal rapporto tra l’errore standard e la media fra i valori teorici: .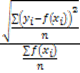

Con il metodo del baricentro ci si può ricavare la retta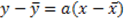

La teoria della regressione si occupa della determinazione di una funzione fra due variabili statistiche adatta a descriverne il possibile legame. Considerate le due rette di regressione di Y su X (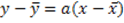) rispetto all’angolo che si forma fra di esse si può dire:

Più l’angolo è piccolo, migliore è il grado di approssimazione dei dati da parte delle due rette;
Se l’angolo è retto, non c’è dipendenza lineare fra le due variabili;
Se l’angolo è nullo, quindi le rette coincidono, la regressione è perfetta.

La correlazione è il valore numerico che mette in relazione le variabili statistiche e si indica con r. Questo prende il nome di coefficiente di correlazione lineare di Bravais-Pearson. r si può calcolare: 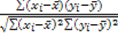(è positivo se a e a₁ sono positivi mentre è negativo se sono entrambi negativi). R è un numero compreso tra -1 e +1:

Se 0<r<1 la correlazione è diretta o positiva;
Se -1<r<0 la correlazione è inversa o negativa;
Se r=1 la correlazione è perfetta diretta (i punti appartengono alla retta di regressione che è crescente);
Se r=-1 la correlazione è perfetta inversa (i punti appartengono alla retta di regressione che è decrescente);
Se r=0 non esiste correlazione lineare.

Dimostrazione funzione interpolante di tipo lineare

Y=ax+b

S(a;b)=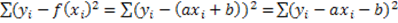

S’a=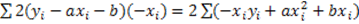

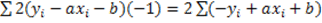
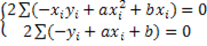
S’b=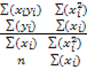

Funzione interpolante di tipo parabolica (quadratica)

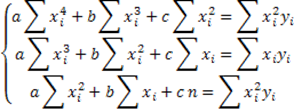
Funzione interpolante di tipo iperbolica

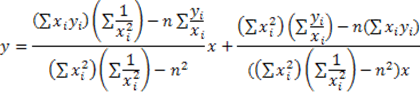
Funzione interpolante di tipo esponenziale

y=ab^x à y=10^q+mx

log(y)= log(a)+xlog(b) z=log(y)

z=q+mx log(a)=q à a=10^q log(b)=màb=10^m

Il calcolo combinatorio serve per evitare elenchi lunghi e noiosi.

DISPOSIZIONE: quando il numero degli elementi da prendere in considerazione è minore al numero degli elementi dell’insieme considerato. L’ordine conta.

D_(n,k)=n(n-1)(n-2)…(n-k+1)= (n!)/(n-k)! ß prodotto di k fattori decrescenti a partire da n n≥k

D’_(n,k)=n^k

PERMUTAZIONE: quando il numero di elementi da prendere in considerazione è uguale al numero degli elementi dell’insieme considerato.

P_n=n(n-1)(n-2)…3*2*1= n!

P_n^a,b=n!/(a!b!)

COMBINAZIONE: quando il numero degli elementi da prendere in considerazione è minore al numero degli elementi dell’insieme considerato. L’ordine non conta.

C_n,k n≥k (D_n,k)/P_k=(n(n-1)..(n-k+1))/k!

Un evento è un avvenimento, descritto da una proposizione, che può accadere o non accadere. Gli eventi che accadono con certezza: eventi certi=1. Gli eventi che non possono mai verificarsi: eventi impossibili =0. Gli eventi che dipendono dal caso: eventi aleatori (da “alea” à dado) tra 0 e 1. Ogni singolo risultato possibile viene detto evento elementare o campione.

La probabilità classica, o a priori, si calcola facendo il rapporto tra i casi favorevoli sui casi possibili (cf/cp).

La probabilità statistica, o a posteriori, si calcola facendo il rapporto tra il numero di volte che si è verificato un evento sul numero delle prove effettuate.

La probabilità soggettiva si calcola facendo il rapporto tra la somma che si è disposti a pagare per il verificarsi di un evento sulla somma che si ottiene in caso di vincita.

Due eventi E₁ e E₂:

Se E₁∩E₂=0 (insieme vuoto) sono incompatibili (nessun caso favorevole ad entrambi)

P_(E1UE2)=P_E1+P_E2

Se E1∩E2≠0 (insieme vuoto) sono compatibili

P_(E1UE2)=P_E1+P_E2-P_(E1∩E2)

Se P(E₁/E₂)=P(E₁) à stocasticamente indipendenti

Se P(E₁/E₂)>P(E₁) à stocasticamente dipendenti positivamente

Se P(E₁/E₂)<P(E₁) à stocasticamente dipendenti negativamente

Evento dipendente: P(E₁/E₂)=P(E₁∩E₂)/P(E₂)

Evento indipendente: P(E₁∩E₂)=P(E₁)*P(E₂)

Prove ripetute o Bernoulli

nà numero di volte che si ripete un esperimento

kà numero di successi

P_(k,n)=(ⁿ _k) p^kq^n-k

Una variabile casuale o aleatoria discreta V è una funzione che associa agli eventi E₁,E₂,…,E_n, incompatibili e complementari fra loro, i valori v₁, v₂,…, v_n. Le probabilità p₁, p₂, …, p_n del verificarsi degli eventi E₁, E₂, … E_n sono così associate ai valori v₁, v₂, …, v_n. L’insieme dei valori v₁, v₂, …, v_n e p₁, p₂, …, p_n è detto distribuzione di probabilità di V.

Il valor medio M(V) di una variabile casuale è la somma dei prodotti dei valori assunti dalla variabile, per le rispettive probabilità: M(V)= v₁*p₁+v₂*p₂+…+v_n*p_n

La variabile statistica è la caratteristica che hanno i caratteri quantitativi di assumere valori diversi. Gli scarti della variabile casuale V dal suo valor medio sono le differenze v₁-M(V); v₂-M(V);…;v_n-M(V).

La varianza var V della variabile casuale V è il valor medio della variabile casuale (V-M(V))², che assume i valori:

σ²(V) o varV= (v₁-M(V))²*p₁ +(v₂-M(V))²*p₂+…+(v_n-M(V))²*p_n

Lo scarto quadratico medio σ²(V) è la radice quadrata della varianza σ(V)=√(varV)

Con il criterio del valor medio (o della speranza matematica) si determina il valore medio per ogni valore e in seguito si considera il maggiore che rappresenta la scelta che l’impresa è propensa ad assumere.

Quindi si imposta una tabella a doppia entrata in cui sono elencate tutte le possibili alternative di scelta al verificarsi di determinati eventi. A lato tutti i possibili eventi e le relative probabilità. Si compila la tabella riportando i valori della variabile casuale che ci interessa, scartiamo una alternativa se risulta dominata dalle altre o la preferiamo se risulta dominante rispetto le altre. In basso nell’ultima riga riportiamo i valori medi della variabile e scegliamo l’alternativa che ha il maggior valor medio se si tratta di guadagno il minor valor medio se si tratta di un costo.

Con il criterio della valutazione del rischio, si fissa una percentuale di rischio che siamo disposti a correre per ritenere vantaggiosa una scelta. La percentuale si riferisce al valor medio, che si calcola per ogni alternativa.

Quindi si calcola il valor medio per ogni alternativa, poi si calcola lo scarto quadratico medio σ di ogni alternativa. Se ci sono due alternative con lo stesso valor medio, scegliamo quella con σ minore. Se ci sono due alternative uguali, fissiamo il rischio massimo o minimo che siamo disposti a correre (M/n, dove se n=1 il rischio è 100%). Si scartano le alternative le quali σ >M/n e si sceglie l’alternativa maggiore se si tratta di guadagni, o minori per i costi.

Con il criterio del pessimista, o maxi-min o min-max, si tiene solo conto degli utili o dei costi. Si considera per ogni utile quello minore, ma poi si prende l’utile maggiore. Viceversa per i costi.

Con il criterio del’ottimista, o maxi-max o min-min, si tiene solo conto degli utili o dei costi. Si considera per ogni utile quello maggiore, e poi si prende l’utile maggiore. Viceversa per i costi, si considera il minore e si prende il minore.

Esistono problemi di scelta in cui le decisioni vanno prese prima che sia noto l’effetto delle attività considerate. È il caso degli investimenti finanziari e degli investimenti industriali dei quali non si conoscono inizialmente i tassi d’impiego. Intendiamo per:

Investimenti finanziari, quelli in cui determinati capitali possono essere investiti con modalità diverse, come depositi bancari, prestiti, acquisto di titoli, acquisto di beni economici, di obbligazioni;
Investimenti industriali, quelli in cui l’azienda deve decidere fra l’acquisto e il noleggio dei macchinari, fra costi di manutenzione, di durata degli impianti, del loro valore dopo un periodo d’uso.

Tra i criteri di scelta per risolvere questi problemi troviamo il criterio dell’attualizzazione e il criterio del tasso di rendimento interno.

Il criterio dell’attualizzazione consiste nel determinare il risultato economico attualizzato. Il risultato economico attualizzato (r.e.a.) di un’operazione di investimento è la differenza tra il valore attuale dei ricavi e il valore attuale dei costi, calcolati entrambi in regime di sconto composto a uno stesso tasso. Si preferisce l’attività che determina il r.e.a. maggiore se si tratta di investimento, il r.e.a. minore se si tratta di un finanziamento. Questo criterio è soggettivo e risente del modo di valutare dell’operatore. Per gli investimenti industriali bisogna tenere conto dei costi di acquisto e manutenzione dell’impianto, il valore di recupero di un impianto a fine uso e la durata dell’impianto o delle macchine. La valutazione deve essere fatta nello stesso momento attraverso la ricerca della scadenza comune degli investimenti o con la durata all’infinito degli investimenti (rendita perpetua: V_a=R(1+1/i) ).

Il valore attuale di un capitale M impiegato per un tempo n al tasso i è: C=M*(1+i)^-n.

Il valore attuale di una rendita posticipata di n rate di valore R al tasso i è: V_a=R*(1-(1+i)^-n)/i.

Il criterio del tasso di rendimento interno consiste nel determinare di ogni attività il tasso interno di rendimento. Il tasso di rendimento interno (t.i.r.), o tasso effettivo d’impiego, di un investimento è quel tasso per il quale i valori attuali dei costi sono uguali a quelli dei ricavi. È il tasso per il quale r.e.a.=0. Si preferisce l’attività che determina il t.i.r. maggiore se si tratta di un investimento oppure t.i.r. minore se si tratta di un finanziamento. Questo criterio è oggettivo e non risente del modo di valutare dell’operatore.

La scelta fra mutuo e leasing si attua quando fra le possibili alternative di un finanziamento ne esiste una che non prevede l’acquisto di un bene da parte dell’operatore, ma solamente un suo affitto. Il criterio consiste nel determinare l’operazione che ha il tasso più basso. Nell’attuazione di questi criteri i calcoli sono spesso complessi. Ci si riferisce allora a tavole con valori calcolati ai vari tassi, o si procede prima per tentativi e poi per interpolazione dei dati ottenuti.

Fonte: http://pitonsblack.altervista.org/s/matetutto.doc

Sito web da visitare: http://pitonsblack.altervista.org

Autore del testo: non indicato nel documento di origine

Nota : se siete l'autore del testo sopra indicato inviateci un e-mail con i vostri dati , dopo le opportune verifiche inseriremo i vostri dati o in base alla vostra eventuale richiesta rimuoveremo il testo.

Matematica riassunti