Algebra

 

---

 

Algebra

 

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

 

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

 

 

 

 

ALGEBRA

 

NOZIONI DI BASE:

Il nome deriva da al-Jabr wa al-muqabala (unione dei numeri) di  Muhammed al-Kwarizmi 800d.C.

Ma le origini del calcolo numerico derivano dalle esigenze commerciali, negli scambi, ma anche nelle costruzioni, le misure dei terreni nonché per gli studi astronomici e le rotte navali.

Consideriamo che le operazioni algebriche funzionano con la medesima logica del pensiero umano.

Siamo ad esempio abituati a dire: sono le 10:30, e che tra 10 minuti saranno le 10:40. In algebra:

 

h = 10°:30’        h₂ = 10°:30’ + 10’ = 10°:40’

 

Il fatto ancora più eclatante è che persino le macchine, come i computer, parlano lo stesso linguaggio, accettano le medesime procedure logiche ed anzi è possibile affermare che la programmazione nei vari linguaggi, da C a Pascal, Fortran, non è nient’altro che l’evoluzione digitale (mediante l’algebra Booleana) dell’algebra classica di cui tratteremo.

 

Un esempio di algebra usata in scienza delle costruzioni:

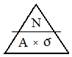
La tensione σ prodotta da una forza N nel corpo di area A, per Navier si rappresenta con: σ = N / A

Ma volendo progettare l’area A conoscendo la σ_ammissibile, posso ribaltare la formula:     A = N / σ_amm     

 

 

L’importanza di queste nozioni non deve essere sottovalutata, pur nella sua semplicità.

 

Operatori logici

Gli operatori logici tra i termini variabili sono noti dai tempi delle elementari:

 

• la somma +
• la sottrazione – 
• la moltiplicazione  ^.  (si omette)
• la divisione / (espressa con le frazioni).

 

Tali segni legano tra loro le incognite e le costanti. Le prime, di solito, vengono scelte tra i primi simboli dell’alfabeto ( a, b, c.. ) o tra gli ultimi ( x, y, z ), più per gli assi di riferimento cartesiani.

 

Equazioni:

La parola equazione nasce dall’esigenza di inserire un segno, l’uguale “ = “ tra due grandezze: una nota ed una incognita. Non sarà mai dato sufficiente risalto all’importanza dell’operatore logico “uguale” ( = ): è di vitale importanza in matematica, ma anche in fisica, o in programmazione: consente di combinare insieme valori noti o costanti con altri valori, opportunamente mantenuti incogniti, per creare una certa legge:

 

altezza = 1,80 m    peso = 80 kg                    in definitiva, ad esempio             x = 30

 

peso = altezza  ^.  sezione  ^.  peso specifico                   oppure                       a = b ^. c ^. d

 

Il simbolo dell’uguale, in definitiva, è da interpretarsi come l’ago di una bilancia: se dispongo un peso da 500 kg su entrambi i piatti, anche se il peso è altissimo, l’ago non si muove.

Attorno all’uguale, con tale criterio, possiamo disporre le grandezze che ci interessano e ogni risposta che appare nell’equazione sarà vera.

 

Lo zero ed i numeri negativi

 

La grande conquista dell’algebra è lo zero (0) ed i numeri negativi (Brahmagupta 600 d.C.):

Non solo alcuni giovani studenti hanno difficoltà a comprendere i numeri negativi: anche il digitale necessita di un complesso sistema per interpretare le cifre negative.

Molto semplice è iniziare ad immaginare un conto in banca: se l’estratto dice che sul mio conto ci sono 100 € (positivi) ma io prelevo (sottraggo) comunque 200 €, il conto è in rosso (negativo) di 100 €, ed i bancari solerti applicano gli interessi passivi per il debito! In algebra:

 

100 – 200 =  – 100

 

Questo è valido anche in campo negativo: se già sono sotto di 100 € e prelevo altri 200 €:

 

– 100 – 200 =  – 300

 

Il fatto che assomigli ad una somma in negativo non è un caso: più avanti impareremo a mettere in evidenza certi valori: in algebra è lecito scrivere l’equazione in questo modo:

 

– ( 100 + 200 ) =  – 300

 

In modo grafico, immaginate dei valori lungo un asse (ad esempio un termometro che ha valori sopra e sotto lo zero). Tutti sappiamo che 3 + 5 = 8, ma pochi comprendono che 3 – 5 =  – 2

 

 

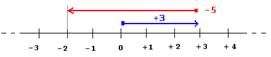
Operazioni algebriche:

Serve sempre ricordare l’importanza del segno = come fosse l’ago di una bilancia, avente a destra e sinistra dei piatti. Se si aggiunge la stessa quantità a destra e sinistra, l’ago non si muove.

Appena genero uno squilibrio, l’ago segna il valore in eccesso. Se immettiamo delle incognite al posto dei valori, apparentemente non si ottiene nulla, ma se infine scopriamo le carte e diamo un valore preciso ad un’incognita, automaticamente risulta il valore preciso dell’altra.

Perciò è necessario prendere confidenza con delle operazioni di base:

 

a + b = 0         →          a =  – b           aggiungo o sottraggo ad ambo i termini la stessa quantità 

 

a ^. b = 1           →         a =  1 / b          moltiplico o divido ambo i termini e semplifico.

 

Nel dettaglio, spostando i termini al di là dell’uguale, per le somme inverto il segno:

 

a + b = 0    →     a + b – b  = 0 – b     →      a =  – b

 

Nella moltiplicazione (o divisione), quello che sta sopra va sotto, e quello che sta sotto va sopra:

 

ab = 1        →        ab   =   1            →        a =  1

        b         b                               b

 

In tal senso è necessario fare una precisazione tecnica: quando due termini si presentano in moltiplicazione come qui sopra a e b, leggendo l’ultima espressione si può dire:

 

a   è l’inverso di   b

 

Se b cresce, a diminuisce, se b diminuisce, a cresce, al fine di mantenere un rapporto fisso espresso nella prima equazione: ab = 1 che non può essere disatteso.

Proprietà dei segni

Nelle moltiplicazioni – divisioni per una quantità negativa si inverte il segno del riultato.

I più rammentano tale principio con la filastrocca:

 

+ ^. + =  +             ;             + ^. –  =  –             ;           –  ^. –  =  +

      più per più fa più     ;     più per meno fa meno  ;   meno per meno fa più

 

Questo vale quando un termine moltiplica altri termini racchiusi tra parentesi:      

 

– 2 ^. ( a + b – c )      →       – 2 a – 2 b + 2 c        per praticità:  2 c – 2 a – 2 b

 

I termini si moltiplicano uno ad uno per il numero, e se il segno è negativo l’effetto è l’inversione del segno. Per praticità, si sconsiglia di scrivere il primissimo termine negativo: invertendo l’ordine dei fattori la somma non cambia, mentre il segno “meno” è più leggibile in tal modo.

Inoltre si può operare l’inversione dei segni, moltiplicando ambo i termini per   – 1 :

 

– a  =  5        →         –1 ^. ( – a )  =  –1 ^. 5         →         a =  – 5

 

 

Semplificare e mettere in evidenza:

Un antico adagio scherzoso recitava: ”conta le pecore per le zampe e divide per quattro”.

In tale modo si voleva evidenziare come sia importante snellire al massimo le espressioni, al fine di evitare ridondanze di calcolo inutili e dispendiose in matematica, in fisica ed in programmazione.

Abbiamo visto prima come due termini opposti si elidono in somma (o sottrazione):

 

a – a = 0      ovvero   3 – 3 = 0

 

Ma le sommatorie ci danno l’occasione di mettere in evidenza una quantità(1) ridondante usando le parentesi. In pratica, il termine che viene “portato fuori” moltiplica tutti i termini nelle parentesi:

 

ab + ac – 2a = 0      →       a ( b + c – 2 ) = 0

 

Da cui ad esempio si evince subito che a = 0 : qualunque valore di b e c viene annullato se a = 0.

 

Nelle moltiplicazioni – divisioni il metodo per semplificare è più evidente: se due termini al numeratore ed al denominatore presentano valori in comune è spesso inutile portarsi tali valori avanti nei calcoli. Trattandosi di divisioni, due termini uguali divisi tra loro fanno 1:

 

 ab + ab   = 10       →       ¹ 2 a b¹ =  2 ^{1 .} 5         →       a = 5

      b                                      ₁ b

 

Questo principio è utile anche in senso inverso: a volte per semplificare bisogna complicare.

Se per esempio vado a moltiplicare una quantità per “uno”, la quantità sappiamo non cambia.

È anche vero che il rapporto fra due quantità uguali è “uno”. Posso allora immettere ovunque in una espressione, un termine adatto ad annullare una certa configurazione, come nel caso della razionalizzazione di un denominatore, per eliminare la radice al denominatore:

 

 1      =      1    .  1     =       1    .   √2        =     √2

√2            √2                     √2       √2                 2

Regole delle frazioni:

Finchè i termini di una sommatoria o di un prodotto vengono a trovarsi tutti in una stessa stringa le difficoltà nell’eseguire modifiche sono evidentemente poche. Appena appaiono termini con le radici, le frazioni e gradi diversi dal primo, anche taluni laureati trovano, imbarazzati, dei problemi.

L’importante, come sempre, è avere chiarezza dell’argomento. Dipende tutto dagli esponenziali, ma  per adesso, basti immaginare la divisione come una forma particolare di moltiplicazione.

Pertanto è possibile semplificare solo i termini simili che moltiplicano, mai che sommano gli altri:

 

 2 a + 6 b – 4 c     =     2 ( a + 3 b – 2 c )    =    a + 3 b – 2 c  

           6                                2 ^. 3                              3

 

Non è possibile altra semplificazione, a meno che non scompongo in parti la frazione:

 

a + 3 b – 2 c    =     a   +   3 b    –   2   c  

         3                    3         3           3

 

Questo semplicemente riporta al seguente principio: quando si moltiplicano le frazioni:

 

 a    .   c      =    ac                si moltiplica “dritto per dritto”

 b        d           bd

 

Quando si sommano due frazioni è diverso: si deve trovare il “minimo comune denominatore”:

 

 a   +   c      =    ad  +  cb                 cercando che “bd” sia minimo.

 b        d                 bd

 

Consideriamo il seguente esempio: due mezze arance fanno un’arancia intera, e su questo non ci piove. Al livello algebrico, un’arancia è la somma di due metà:

 

 1   +    1   =     1  +  1    =   2   =  1

 2         2              2              2

 

Mentre se considero la metà della (per la) metà, sto considerando la metà di mezza arancia, ovvero, un quarto di arancia:

 

 1    x    1   =      1  x 1      =   1   

 2          2           2  x 2           4

 

Un’ultima difficoltà è rappresentata dalle frazioni di frazioni. Anche qui serve usare la logica: il segno di frazione rappresenta il segno di divisione “ : “. L’unica regola da ricordare è che quando inverto da “diviso” a “per”, la frazione si ribalta. Osserviamo l’esempio:

 

  a

  b      =     a   :   c       =      a   .   d     =    ad

  c             b       d               b       c            bc

  d

 

Nelle espressioni che spesso vengono date e nelle future applicazioni, potrebbero esserci vari termini tutti racchiusi tra parentesi da spostare e semplificare internamente ad un’espressione.

Ma tali modifiche seguono le stesse regole di una delle variabili a, b, c, d finora viste, fintanto che fanno parte del medesimo blocco, tra le parentesi.

 

 

 

Fonte: http://www.webalice.it/greendog/cs/files/matematica10.doc

Autore del testo: non indicato nel documento di origine

Parola chiave google : Algebra tipo file : doc

 

APPUNTI DI ALGEBRA

 

Punti, vettori, prodotto scalare.

 

Punto                         è rappresentato da un insieme di numeri (x1, x2....xn) tanti quante sono le dimensioni Dello spazio.

 

n-pla                           insieme di numeri (x1, x2....xn) che rappresenta un punto in un n-spazio.

 

Coordinate                i numeri (x1, x2....xn) che rappresentano il punto.

 

Addizione                  se A, B sono punti nello spazio A + B = (a1+b1 + ... + an+bn).

Tra punti

 

Punto moltiplicato    se A è un punto e c è una costante, cA = (ca1, ..., can).

Per 1 costante

 

Proprietà dell’           1)   (A+B) + C = A + (B + C)

Addizione tra punti  2)   A + B = B + A

                                   3)   c(A+B) = cA + cB

                                   4a) (c1 + c2)A = c1A + c2A

                                   4b) (c1 * c2)A = c1(c2 * A)

                                   5)    0 = (0, 0, ..., 0)    A + 0 = A

                                   6a)  A * 1 = A

                                   6b)  (-1)A = -A;          A + (-A) = 0

                                    una coppia ordinata di punti. Si scrive AB (con la freccia sopra, ma non indica il prodotto) dove A si dice origine del vettore e B si dice fine del vettore. Se si ha un vettore formato da 1 sola ennupla lo si considera applicato all’origine (il punto 0, 0, ..., 0).

 

Vettori applicati        se abbiamo AB e CD, i vettori si dicono equivalenti se O(B-A) = O(D-C).

equivalenti                 Geometricamente se, una volta applicati all’origine, risultano avere la stessa direzione, verso e lunghezza.

 

Vettori paralleli         AB e CD sono paralleli se esiste una costante c ¹ 0 tale che B-A = c(D-C). Geometricamente se hanno la stessa direzione, in più se c > 0 hanno anche lo stesso verso, altrimenti sono di verso opposto.

 

Vettori                        AB è perpendicolare a CD se B-A è perpendicolare a D-C, ovvero il prodotto

perpendicolari           scalare  (B-A)(D-C)  è uguale a zero. Altra condizione di perpendicolarità: ||A+B|| = ||A-B||

 

Prodotto scalare        se A e B sono 2 vettori, il loro prodotto scalre si scrive A*B e si ottiene in

Tra 2 vettori              questo modo: A*B = (a1*b1 + ... + an * bn). Il prodotto scalare è un numero.

 

Proprietà del             1) A*B = B*A

Prodotto scalare        2) A*(B+C) = A*B +A*C

                                    3) (xA)*B = x(A*B)              x = costante.

                                    4) se A = 0 (vettore nullo), allora A*A= 0. se A ¹ 0, allora A*A > 0

 

Norma di un              detta anche lunghezza o modulo, si tratta del suo valore preso sempre positivo vettore                si scrive |A|.

 

Vettori con la            A e B hanno la stessa direzione se esiste un c>0 tale che cA=B

Stessa direzione

 

Distanza tra 2 punti  distanza tra 2 punti A e B: |A-B|

 

Proiezione di A su B se A, B sono 2 vettori e c una costante, cB è detta proiezione di A su B, dove c = A/B.

 

Angolo tra A e B       L’angolo individuato da 2 vettori con lo stesso punto di applicazione è

cosa = __AB__

            ||A||*||B||

 

Rette e piani

 

Equazione                  dato P = punto e A = vettore, l’equazione parametrica è definita come

Parametrica della      x = P + tA.

Retta

 

Iperpiano                   piano passante per un punto P e perpendicolare  ad un vettore N (non nullo). Oppure è l’insieme di tutti i punti tali che X-P è perpendicolare a N: (X-P)N = 0. In alternativa si può definire come il piano passante per P e perpendicolare alla retta (vettore) N.

 

Rette parallele           presi 2 punti P1, Q1 su una retta e P2, Q2 sull’altra retta, esse si dicono parallele se i vettori P1-Q1 e P2-Q2 sono paralleli.

 

Piani paralleli            2 piani sono paralleli se i loro vettori normali (perpendicolari) sono paralleli.

 

Angolo tra 2 piani     è lo stesso angolo formato da 2 vettori normali appartanenti ai 2 piani.

 

Numeri complessi

 

Definizione di            1) Ogni numero reale è un numero complesso.

Numero complesso    2) Esiste un numero complesso i tale che i² = -1.

3) ogni numero complesso può essere scritto in modo unico come a + bi,

    essendo a, b numeri reali.

4) tutte le proprietà di addizione e moltiplicazione continuano a valere.

 

Addizione di              x = a1 +b1i, y = a2 +b2i.  x+y = (a1+a2) + (b1+b2)i

Numeri complessi

                                                                                       _                                 _

Coniugato di un        se X = a + bi, il suo coniugato è X = a –bi. Dunque X*X = a²+b²

Numero complesso

                                                                                     _

Proprietà dei             1)X = a + bi (non nullo) k = __X__ è il suo coniugato e viene scritto k^-1

Numeri complessi                                                    a²+b²

                                               2) a, b numeri complessi, |a+b| £ |a| + |b|

                                   3) a, b numeri complessi, |ab| = |a|*|b|

 

 

Valore assoluto di     dato k = a + b1. il valore assoluto è come al solito il numero preso

un come numero       positivo e in questo caso coincide con la lunghezza del vettore (a,b).

complesso      

 

Spazi vettoriali

 

Rⁿ                                insieme di tutte le ennuple ordinate di numeri reali.

 

Corpo (di numeri)    un insieme di numeri complessi k è un corpo se soddisfa le seguenti prop.

• dati x, y Î k, x+y Î k e xy Î k
• se x Î k Þ -x Î k. Se x ¹ 0 Þ x ^–1 Î k
• 0 Î k e 1 Î k.

Gli insiemi dei numeri razionali, dei reali e dei complessi sono corpi.

 

Sottocorpo                 un sottoinsieme di un corpo che soddisfa le proprietà del corpo.

 

Spazio vettoriale        è definito su un corpo ed è un insieme che supporta l’addizione e la moltiplicazione ed inoltre gode delle seguenti proprietà:

                                    1) " u,v,w Î V          (u+v)+w = u+(v+w)               (V= spazio vettoriale)

                                    2) $ 0 Î V:                 " u Î V:         0 + u = u + 0 = u

                                    3) " u Î V:                u + (-1u) = 0

                                    4) " u, w Î V            u + w = w + u

                                    5) c = costante                       c(u + w) = cu + cv

                                    6) a, b numeri             (a + b)v = av + bv                  (v Î V)

                                    7) a, b numeri             (ab)v = a(bv)

                                    8) " u Î V                 1*u = u

 

sottospazio                 sottoinsieme di uno spazio vettoriale che gode delle seguenti proprietà:

vettoriale                    1) se u, w Π W          Þ        u + w Î W

                                   2) se u, w Π W          Þ        u * w Î W

• 0 Î W

 

vettore                        elemento di uno spazio vettoriale Rⁿ, dove R è il corpo dello spazio vettoriale

                                    ed n è il numero di dimensioni dello spazio, cioè il numero di elementi presenti nel vettore.

 

Combinazione           dato un insieme di vettori (v₁, … , v_n) e un insieme di numeri (x₁, … , x_n)

Lineare                      definiamo la combinazione lineare come (v₁x₁ + … + v_n x_n).

 

Sottospazio generato l’insieme di tutte le combinazioni lineari possibili con i vettori (v₁, …

Da  (v₁, … , v_n)                      , v_n).

 

 

Generatori di uno     l’insieme di tutte le combinazioni lineari dei vettori (v₁, … , v_n).

Spazio vettoriale

 

Funzione (a valori)    regola tramite la quale si asociano elementi di un insieme con elementi di un altro insieme.

 

Basi

 

Vettori linearmente   presi dei vettori da uno spazio vettoriale V sul corpo K, essi si dicono

Dipendenti                 linearmente indipendenti se esistono n elementi (a₁, … , a_n) Î K (non tutti nulli) tali che a₁v₁ + … + a_n v_n = 0.

 

Vettori linearmente   dei vettori (v₁, … , v_n) tale che  non esistono n elementi (a₁, … , a_n) Î K (non

indipendenti              tutti nulli) tali che a₁v₁ + … + a_n v_n = 0.

 

Base dello spazio       se un insieme di vettori (v₁, … , v_n) sono generatori di V e sono linearmente

Vettoriale V               indipendenti, allora si dicono base di V.

 

Coordinate del          se presa una base (w₁, … , w_n), il vettore v si può scrivere come (a₁w₁ + … +

Vettore v rispetto      a_n w_n), (a₁, … , a_n) sono le coordinate del vettore v rispetto alla base.

A una base

 

Vettore delle              il vettore (a₁, … , a_n) di elementi attraverso i quali si può rappresentare un

Coordinate                vettore rispetto alla sua base.

 

Sottinsieme                preso un sottoinsieme (v₁, … , v_r) con 0 < r £ n, da un insieme di elementi 

Massimale di              (v₁, … , v_n) di uno spazio vettoriale V, diremo che (v₁, … , v_r) è sottoinsieme

Elementi                     massimale di elementi linearmente indipendenti se:

Linearmente              1) (v₁, … , v_r) sono linearmente indipendenti.

Indipendenti              2), ogni elementov_i con i > r, gli elementi (v₁, … , v_r, v_i) sono linearmente dipendenti.

 

Dimensione di uno    numero di elementi di cui è costituita la base di uno spazio vettoriale V. Si

Spazio vettoriale        indica con dimV.

 

Insieme massimale    degli elementi di V, (v₁, … , v_n), sono un insieme massimale di elementi

Di elementi linearm. Linearmente indipendenti se (v₁, … , v_n) sono linearmente indipendenti e per

Indipendenti              ogni elemento w Î V (w, v₁, … , v_n) sono linearmente dipendenti.

 

 

Somme e somme dirette.

 

Somma                       Dati U e W sottospazi di V, la loro somma è data dal sottoinsieme di V costituito da tutte le possibili somme u + w con u Î U e v Î W.

 

Somma Diretta          uo spazio vettoriale V è somma diretta di 2 sottospazi U e W se ogni elemento di V può essere scritto come u + w, con u Î U e v Î W.

                                    Si scrive: V = U Å W.

 

Addizione di              se U e W sono spazi vettoriali qualsiasi sul corpo K, definiamo l’addizione

elementi di spazi        come (u₁ + w₁) + (u₂ + w₂), con  (u₁, w1) e (u_2, w₂) Î UxW.

vettoriali

 

Prodotto diretto        se U e W sono spazi vettoriali qualsiasi sul corpo K, definiamo prototto diretto il risultato c(u+v), con u Î U e v Î W e c Î K.

 

Matrici

 

Matrice                      Preso un corpo K, definiamo matrice come una serie di elementi disposti su m righe e n colonne. Dove ogni elemento a_ij è definito come componente o termine della matrice.

 

Vettore Colonna       m-pla ricavata da una colonna di una matrice.

 

Matrice Quadrata     matrice col numero di righe pari al numero di colonne.

 

Matrice zero              matrice avente come elementi tutti zeri.

 

Addizione tra            Viene effettuata componente per componente e può essere effettuata solo

Matrici                       quando le due matrici hanno le stesse dimensioni.

 

Matrice Trasposta    Data una matrice, la sua trasposta si indica con ^tA ed è costituita dalla matrice stessa con le righe al posto delle colonne. Per esempio una matrice 3x2 diventa una matrice 2x3.

 

Matrice Simmetrica  Una Matrice si dice simmetrica quando coincide con la sua trasposta.

 

Matrice diagonale     Matrice avente tutte le sue componenti nulle, ad eccezione di quelle diafgonali. Ogni matrice diagonale è anche simmetrica.

 

Matrice unità             Matrice quadrata con tutte le componenti nulle ad eccezione di quelle diagonali che sono uguali ad 1. Viene denotata con I_n  oppure con I.

 

Prodotto Scalare       viene effettuato componente per componente e gode delle seguenti proprietà:

Tra Matrici                PS1.    se A, B sono nel corpo Kⁿ, AB = BA

                                    PS2.    se A,B,C sono in Kⁿ, A(B + C) = AB + AC = (B + C)A

                                    PS3.    se x Î K, (xA)B = x(AB) e A(xB) = x(AB)

                                    Non degenerazione:   Se A Î Kⁿ, e se per ogni X Î Kⁿ AX = 0 allora  A=0

 

Prodotto tra               Può essere eseguito solo se il numero di righe della prima matrice è uguale

Matrici                       al numero di colonne della seconda. Date 2 matrici A m´n e B n´s, gli elementi della matrice prodotto si ottengono moltiplicando  i vettori riga di A per i vettori colonna di B(dunque moltiplicando i songoli elementi del vettore e poi addizionandoli per ottenere l’elemento della matrice prodotto) ottenendo cosi’ una matrice m´s.

 

Matrice Invertibile    Detta anche matrice non singolare, è una matrice quadrata A per cui esiste una matrice B delle stesse dimensioni che moltiplicando A*B oppure B*A, si ottiene una m,atrice unità I_n. In pratica: AB = BA = I_n. La matrice B viene detta inversa di A e viene denotata con A^-1.

 

Matrici con                Sia A una matrice quadrata. Definiamo la matrice A^m come la matrice

Esponenti                   moltiplicata m volte per sé stessa. Con A⁰ indichiamo la matrice unità avente le stesse dimensioni di A e con A¹ la matrice stessa.

 

Matrice Nilpotente    Matrice quadrata A per cui esiste un iintero r>0 tale che A^r=0.

 

Equazioni Lineari

 

Equazioni Lineari     Equazioni  nella forma  a₁₁x₁  + … +  a_1nx_n = b₁

                                                                                                  a_m1x₁ + … +  a_mnx_n = b_m

 

Sistema Omogeneo    Sistema di equazioni lineari come sopra descritto, dove tutti i termini b_{1 …} b_m sono nulli.

 

Matrice dei                Preso un sistema lineare, la matrice dei coefficienti è quella formata da tutti

coefficienti                 gli elementi a_{11 …} a_1n , …, a_{m1 …} a_mn

 

Sistema Omogeneo   Sistema Omogeneo ottenuto da un sitema di equazioni linerari ponendo i

Associato                   termini b_{1 …} b_m pari a zero.

 

 

Applicazioni Lineari

 

Applicazione              Modo di associare gli elementi di un insieme agli elementi di un altro insieme.

 

Immagine                   presa un’applicazione S®S¹ ed un elemento sÎS, si dice immagine di s l’elemento di S¹ che viene associato ad s dall’applicazione. Viene detta anche valore di s.

 

Funzioni                     Presa un’applicazione F: S ® Kⁿ, dato che per ogni elemento di S avremo un

Coordinate                vettore F(t) = (f₁(t), ... , f_n(t)) come risultato dell’applicazione, gli elementi del vettore vengono chiamati funzioni coordinate.

 

Curva in forma         Se abbiamo un’applicazione F: J ® Rⁿ, con J intervallo di numeri reali, allora

Parametrica              l’applicazione viene detta curva nell’n-spazio.

 

Applicazione             Applicazione F: V ® V¹ sul corpo K, con V, V¹ spazi vettoriali, per cui

Lineare                      valgono le seguenti proprietà:

                                    AL1 -              " u, v Î V:                 F(u + v) = F(u) + F(v)

                                   AL2 -              "c Î k, " v Î V:        F(cv) = cF(v)

 

Applicazione             Dato V spazio vettoriale, l’applicazione identica è quella che associa ad ogni

Identica                      elemento u di V sè stesso, è un applicazione lineare a viene denotata con id.

 

Applicazione             Viene definita su spazi vettoriali, ed è quell’applicazione che associa ad ogni

Nulla                          elemento di V l’elemento 0. Detta anche applicazione zero.

 

Spazio delle               dati 2 spazi vettoriali V e V¹, definiamo spazio delle applicazioni lineari

Applicazioni              l’insieme di tutte le applicazioni lineari da V a V¹. Viene indicato con

Lineari                       L(V, V¹), oppure L se il riferimento agli spazi vettoriali è chiaro.

 

Somma di                  Date 2 applicazioni lineari T: V ® V¹ e F: V ® V¹, definiamo la loro somma

Applicazioni              T + F come l’applicazione il cui valore in u è pari a T(u) + F(u).

Lineari

 

Nucleo                                   data F: V ® W applicazione lineare, l’insieme di elementi v Î V tali che

                        F(v) = 0 è detto nucleo di F. Il nucleo è sempre un sottospazio di V.

 

Piano                          dati 2 vettori linearmente indipendenti nell’n-spazio e P un punto dell’n-spazio, l’insieme dei punti X tali che: X = P + tA + uB, dove t e u assumono tutti i valori reali è detto piano passante per P e parallelo ad A e B. l’equazione X = P + tA + uB è chiamata equazione parametrica di un piano.

 

Immagine di una       data F: V ® W applicazione lineare, si definisce immagine di F l’insieme di

Applicazione              elementi w Î W per i quali esiste un elemento v Î V tale che F(v) = w.

Lineare                      l’immagine di F è un sottospazio di W.

 

Applicazione              applicazione F: S ® S¹, dove comunque si prendano elementi t, u in S, risulta

Iniettiva                      F(t) ¹ F(u). F è iniettiva se e solo se il nucleo di F è {0}.

 

Applicazione              applicazione F: S ® S¹ in cui l’immagine di F è l’intero insieme S¹. In pratica

Surgettiva                  è surgettiva se ogni elemento di S¹ è associato ad un elemento di S.

 

Applicazione              data F: V ® W applicazione lineare, diciamo che F è invertibile se esiste una

Lineare                      applicazione lineare G: W ® V tale che F ° G = id e G ° F = id.

Invertibile

 

Isomorfismo              Applicazione lineare sia iniettiva che surgettiva (dunque anche invertibile). Se si vuole specificare che l’isomorfismo è sul corpo K, si parla di K-isomorfismo.

 

Operatore                  Applicazione lineare di uno spazio vettoriale in sè stesso del tipo F: V ® V.

 

Applicazioni Lineari e Matrici

 

Matrice associata      prendiamo un’applicazione lineare F: V ® W e  2 basi di V e W, {v₁, ... v_n}

All’applicazione        {w₁, ... w_m}. Gli elementi F(v₁) ... F(v_n), i risultati dell’ applicazione, 

Lineare F                   appartengono a W, ed  ognuno di questi può dunque essere scritto come combinazione lineare di w₁, ... w_m. Presi i coefficienti a₁ ... a_n  delle combinazioni lineari così ottenute, costruiamo una matrice, la cui trasposta sarà chiamata matrice associata all’applicazione lineare F.

 

Applicazione              un applicazione lineare F: V ® V di dice diagonalizzabile se esiste una base

Diagonalizzabile        B per  cui la relativa matrice associata a F è una matrice diagonale.

 

Matrici Simili             Due matrici M, M¹ si dicono simili in un corpo K se esiste una matrice invetibile N tale che M¹ = N^-1*M*N.

 

Notazione M^b_b1(F)     la notazione M^b_b1(F) viene usata per indicare la matrice associata all’applicazione lineare F: V ® W, relativa alle basi b e b¹, con b Î V e b¹Î W. Se le basi sono già fissate si può anche scrivere M(F).

 

Determinanti

 

Determinante di        Data una matrice quadrata 2 x 2  con la prima riga (a, b) e la seconda (c, d)

Matrice 2 x 2             definiamo il suo determinante come il numero ad – cb. Il determinante di una matrice costruita in questo modo gode delle seguenti proprietà:

• Il  determinante, come funzione dei vettori colonne, è lineare.
• Se due colonne sono uguali, allora il det. è uguale a 0.
• Il det.e di una matrice unità 2 x 2 è uguale a 1.
• Se si addiziona a una colonna un multiplo di un’altra colonna, il valore del det. non cambia.
• Se due colonne sono scambiate tra di loro, il det. cambia di segno.
• Il det. di una matrice e della sua trasposta sono uguali, det D(A) = D(^tA).
• I vettori (a, c) e (b, d) sono linearmente indipendenti se e solo se il det.   ad – bc è uguale a 0.

 

Sviluppo del              Si applica a matrici quadrate e viene applicato nel seguente modo:

Determinante                        - si decide una riga secondo la quale calcolare il determinante e la si elimina

Secondo la riga         - si prende la prima colonna, la si elimina e si moltiplica la matrice così creata

i-esima                           per il numero dato dall’intersezione tra la riga e la colonna eliminate.

- si aggiunge questo risultato alla soluzione finale che ci darà il det. della 

   matrice scelta, secondo la regola che le matrici ottenute da colonne dispari

   si sommano e le matrici ottenute da colonne pari si sottraggono.

 

Matrice Inversa         Data una matrice A di dimensione n x n, se abbiamo una matrice B tale che AxB = BxA = I, dove I è una matrice unità, allora B è la matrice inversa di A e viene denotata con A^-1.

 

Determinante di        Sia A: V ® V un’applicazione lineare, sia M = M^b_b(A) la matrice associata

Un’applicazione        ad A rispetto alla base b. Il determinante di questa matrice è indipendente

Lineare                      dalla base e rapprensenta il det. dell’applicaizone lineare A.

 

Proprietà del det.      1)         se A, B sono 2 applicazioni lineari da V a V,

Di un’applicazione               allora D(AB) =  D(A)*D(B).

Lineare                      2)         se A è invertibile, allora D(A^-1) = D(A)^-1.

                                   3)         Se I è l’applicazione identica, allora D(I) = 1.

4)         Un’applicazione lineare dello spazio V in sè stesso è invertibile, se e solo se, il suo determinante è diverso da 0.

 

 

Permutazioni

 

Permutazione            Dato un insieme di interi J, una permutazione è un’applicazione F: J®J tale che se x ¹ y, allora F(x) ¹ F(y).

 

Permutazione            L’applicazione inversa F^-1 che, per ogni x Î J, se F(x) = y allora F^-1(y) = x.

Inversa

 

Applicazione              se F e G sono permutazione, possiamo considerare anche l’applicazione

Composta                  composta F°G, o più semplicemente FG che è ancora una permutazione.

 

Trasposizione            è una permutazioneche scambia solo 2 numeri dell’insieme e lascia gli altri al loro posto.

 

Permutazione            Permutazione a il cui segno assegnato dal numero t(a)  è 1.

Pari

 

Permutazione            Permutazione a il cui segno assegnato dal numero t(a)  è –1.

Dispari

 

Polinomi e matrici

 

Polinomio                   un polinomio sul corpo K è una funzione f: K ® K tale che esistono in K elementi a₀, ..., a_n tali che f(t) = a_ntⁿ + ... + a₀ per ogni t Î K.

 

Coefficienti di un      dato un polinomio f(t) = a_ntⁿ + ... + a₀ i numeri a₀, ..., a_n sono detti coefficienti,

polinomio                   in particolare a₀ è detto termine costante di f.

 

Polinomio lineare      un polinomio di grado 1.

 

Radice di un              dato un polinomio f, un numero a tale che f(a) = 0 viene denominato radice

Polinomio                   di f.

 

Molteplicità di           dato un polinomio f nel corpo complesso C, esso può essere scritto come:

Una radice                 f(t) = (t - a₁)^m1 ... (t - a_r)^mr, dove a₁, ..., a_r sono radici distine del polinomio e m₁, ..., m_r  sono interi positivi univocamente determinati. Dato un termine m_i del polinomio diciamo che esso è la molteplicità della radice a_i.

 

Autovettore               dato uno spazio vettoriale V su K, e un operatore di V A: V ® V, un elemento v Î V è detto autovettore di A se in K esiste a tale che Av = av.

                                    Se v ¹ 0, a è univocamente determinato dato che a₁v = a₂v Þ a₁ = a₂. Gli autovettori vengono anche chiamati vettori caratteristici.

 

Autovalore                 dato un operatore A: V ® V su K e autovettore v, per cui ovviamente Av = av, il numero a viene chiamato autovalore se è univocamente determinato. Gli uotovalori vengono anche detti valori caratteristici.

 

Polinomio                   Data una matrice A di dimensioni n x n sul corpo K, A = (a_ij), il polinomio

Caratteristico            caratteristico è il determinante P_A(t) = det(tI – A). Ovvero il determinante della matrice con i termini invertiti di segno ed avente per diagonale elementi del tipo t - a_ij, dove a_ij è un elemento della diagonale della matrice.

 

Polinomio                   Prendiamo un’applicazione lineare A: V ® V, in uno spazio vettoriale di

caratteristico per       dimensione finita. Definita una base di V consideriamo la matrice M che

un’applicazione         rappresenta A rispetto a V. Il polinomio caratteristico di M è anche il

lineare                        polinomio caratteristico per l’applicazione lineare A.

 

Molteplicità di un      Dato un autovalore a dell’applicazione lineare A, la sua molteplicità è pari

Autovalore                alla radice del polinomio caratteristico di A.

 

 

 

 

 

Gruppi

 

Gruppo                      Insieme G a cui è assegnata una regola  che permette di associare ad ogni

Moltiplicativo            coppia (x,y) di elementi di G, un elemento di G stesso denotato xy che soddisfa le seguenti proprietà:

                                    1)        " x, y, z:         (xy)z = x(yz)                                      (associativa)

                                    2)        $ a Î G :        " x Î G,         ax = xa = x                (elem. neutro)

                                    3)        " x Î G:         $ y Î G,          xy = yx = a                (simmetrica)

 

Gruppo                      Gruppo per il quale il risultato dell’associazione tramite legge di

Additivo                     composizione è x + y invece di xy. Le proprietà a cui deve sottostare l’elemento x + y sono le seguenti:

                                    1)        " x, y, z:         (x + y) + z = x + (y + z)                     (associativa)

                                    2)        $ a Î G :        " x Î G,         0 + x = x + 0 = x        (elem. neutro)

3)        " x Î G:         $ y Î G,          x + y = y + x = a        (simmetrica)

 

Gruppo Abeliano      gruppo moltiplicativo  in cui, oltre alle proprietà suddette, viene soddisfatta anche la seguente proprietà:

                                    4)        " x, y Î G      x + y = y + x.                                     (simmetrica)

                                    Viene detto anche gruppo commutativo.

 

Gruppo lineare         Gruppo formato dalle matrici invertibili n x n, rispetto alla moltiplicazione,

generale                     viene denotato con GL_n(K), oppure GL(n,K).

 

Gruppo lineare         Gruppo formato, rispetto alla moltiplicazione, dalle matrici invertibili n x n su

Speciale                      corpo K aventi determinante uguale a 1.

 

Gruppo banale          Gruppo con un solo elemento.

 

Gruppo finito            Gruppo con un numero finito di elementi.

 

Ordine di un              Numero di elementi di un gruppo.

Gruppo

 

Prodotto diretto        Gruppo G x G¹ ottenuto da due gruppi G, G¹ e costituito da tutte le coppie ordinate (x,x¹), con x, Î G e x¹ Î G¹. il prodotto diretto gode della seguente proprietà:

Prese 2 coppie di G x G¹, è possibile definire il loiro prodotto (xy,x¹y¹).

 

Fonte: http://twiki.dsi.uniroma1.it/pub/Users/LucaPastorello/Lang-appuntidialgebra.doc

Autore del testo: non indicato nel documento di origine

Parola chiave google : Algebra tipo file : doc

 

Algebra

 

 

 

 

 

Visita la nostra pagina principale

 

Algebra

 

Termini d' uso e privacy