• 
• 

 

Matematica domande e risposte

 

 

---

 

Matematica domande e risposte

 

I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

Matematica

 

I . GONIOMETRIA

 
Misura degli angoli e degli archi.

1. NEL SISTEMA SESSAGESIMALE SI ASSUME COME UNITÀ DI MISURA
a) la novantesima parte dell’angolo retto cui si dà il nome di angolo grado.
b) quell’angolo al centro di una qualsiasi  circonferenza il cui arco corrispondente è di lunghezza
uguale al raggio (angolo radiale o radiante)
c) la novantesima parte di un angolo qualsiasi preso in senso orario.
d) la novantesima parte di un angolo qualsiasi preso in senso antiorario.

2. NEL SISTEMA RADIALE SI ASSUME COME UNITÀ DI MISURA

• la novantesima parte dell’angolo retto cui si dà il nome di angolo grado.
• la novantesima parte di un angolo qualsiasi preso in senso orario.
• la novantesima parte di un angolo qualsiasi preso in senso antiorario.
• quell’angolo al centro di una qualsiasi circonferenza il cui arco corrispondente è di lunghezza uguale al raggio (angolo radiale o radiante)

3. IL VALORE IN RADIANTI DI 180° (CENTOTTANTA GRADI) È
a)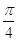 
b)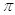 
c) 2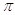
d) 12

4. IL VALORE IN RADIANTI DI 90° È
a)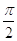
b)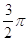
c) 2
d)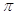

5. IL VALORE IN RADIANTI DI 45° È
a)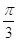
b)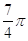
c)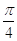
d) 7

 

 

 

6. IL VALORE IN RADIANTI DI 60° È
a)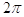
b)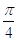
c)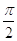
d)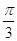

7. IL VALORE IN RADIANTI DI 30° È
a)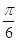
b)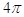
c)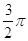
d) 2

8. IL VALORE IN RADIANTI DI 270° È
a)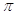
b) 2p
c)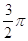
d)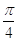

9. IL VALORE IN RADIANTI DI 360° È
a)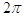
b)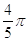
c)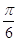
d) 15

10. IL VALORE IN RADIANTI DI 120° É
a)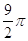
b)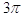
c)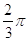
d)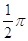

 

 

 

11. LA LUNGHEZZA l DELL’ARCO DI CIRCONFERENZA (VEDI FIGURA)  
IL CUI RAGGIO r È CM. 6 E IL CUI ANGOLO AL CENTRO a° = 50°   È PARI A

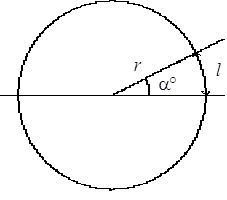
a) 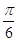 cm                                   
b) cm
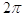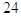c) cm
d) 2 cm

12. LA LUNGHEZZA  l  DELL’ARCO DI CIRCONFERENZA IL CUI RAGGIO,  r  È CM. 20 E IL CUI ANGOLO AL CENTRO  a° = 18° È PARI A
a) 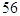cm
b) cm
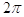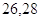c) cm
d) 13 cm

13. LA MISURA IN GRADI DI UN ARCO DI CIRCONFERENZA LA CUI LUNGHEZZA l È 2p CM E IL CI RAGGIO r È 4CM, È PARI A:
a) 21°
b) 90°
c) 10°
d) 15°

14. LA MISURA IN GRADI DI UN ARCO DI CIRCONFERENZA LA CUI LUNGHEZZA l È 4p CM E IL CI RAGGIO r È 4CM, È PARI A:
a) 70°
b) 10°
c) 270°
d) 180°

 

 

 

 

La circonferenza goniometrica e le funzioni goniometriche

 

definizioni di funzioni circolari e goniometriche

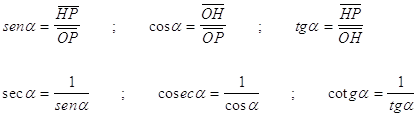
dove 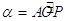 (angolo) per la definizione di funzioni goniometriche
mentre 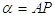 (arco) per la definizione di funzioni circolari

15. LE  FUNZIONI SENO E COSENO SONO PERIODICHE DI PERIODO
a) 2p
b) p/2
c) p
d) 4p

16. LA FUNZIONE TANGENTE È PERIODICA DI PERIODO
a) 2p
b) p/2
c) p
d) p/3

17. LA FUNZIONE COTANGENTE È PERIODICA DI PERIODO
a) 2p
b) p/2
c) p/4
d) p

18. LA FUNZIONE SENO È POSITIVA NEL
a) primo quadrante
b) secondo quadrante
c) terzo quadrante
d) quarto quadrante

 

19. LA FUNZIONE COSENO È NEGATIVA NEL
a) primo quadrante
b) secondo quadrante
c) terzo quadrante
d) quarto quadrante

 

20. LA FUNZIONE TANGENTE È POSITIVA NEL
a) primo quadrante
b) secondo quadrante
c) terzo quadrante
d) quarto quadrante

 

Relazioni fondamentali fra le funzioni goniometriche di uno stesso angolo o arco.

 

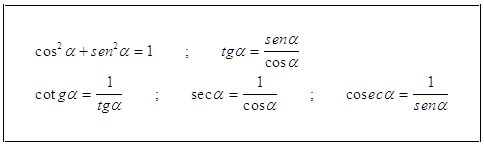
21. I VALORI ASSUNTI DA cos a E tg a QUANDO sena = 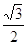, CON 0° < a < 90°, SONO RISPETTIVAMENTE

        Cos a              Tga

     a)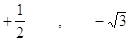
b)
c)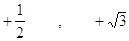
d)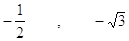

 

 

 

 

22. I VALORI ASSUNTI DA cos a E sena QUANDO tga = 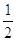, CON 180°< a < 270°, SONO RISPETTIVAMENTE

         Cosa                       Sena

     a)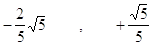 
b)
c)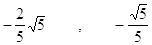 
d)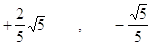

23. IL VALORE DELLA SEGUENTE ESPRESSION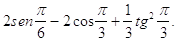E
 È:
a)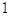
b)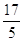
c)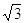
d) 0

24. IL VALORE DELLA SEGUENTE ESPRESSION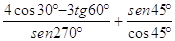E:   È
a)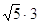
b)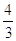
c) 1
d)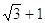

 

Archi supplementari, archi che differiscono di una semicirconferenza, archi esplementari*, archi complementari, archi che differiscono di un quadrante .
25. IL VALORE DELLA SEGUENTE ESPRESSION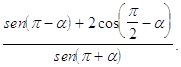E:  È
a)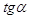
b)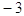
c)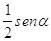
d) 0

 

26. IL VALORE DELLA SEGUENTE ESPRESSION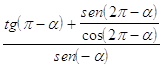E: . È
a)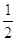
b)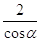
c)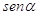
d) 1
27. IL VALORE DELLA SEGUENTE ESPRESSION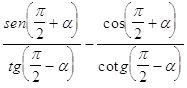E: . È
a)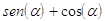
b)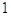
c)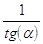
d) 0

 

Riduzione al primo quadrante

 

28. LA CORRETTA RIDUZIONE AL PRIMO QUADRANTE DELLE SEGUENTI FUNZIONI GONIOMETRICHE , È
a)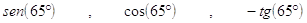
b)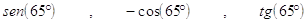
c)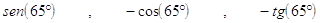  
d)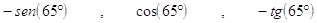

29. LA CORRETTA RIDUZIONE AL PRIMO QUADRANTE DELLE    SEGUENTI FUNZIONI GONIOMETRICH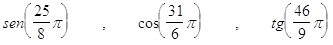E , È
a)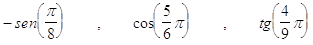
b)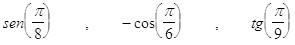
c)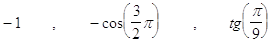
d)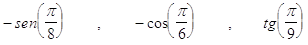

 

 

 

Formule di addizione e sottrazione

30. USANDO LE FORMULE DI ADDIZIONE E SOTTRAZIONE CALCOLARE 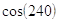  ,    ,    , E INDICARE LA RISPOSTA ESATTA.
a) -1/2  ,    ,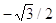 
b) -1/2  ,    ,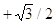 
c) -1/2  ,    ,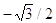 
d) +1/2  ,    ,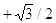 

31. USANDO LE FORMULE DI ADDIZIONE E SOTTRAZIONE CALCOLARE:   ,    ,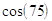  
a)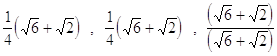
b)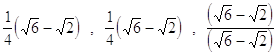
c)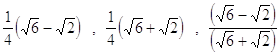
d)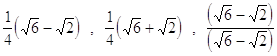

Formule di duplicazione

 

32. USANDO LE FORMULE DI DUPLICAZIONE E DI ADDIZIONE E SOTTRAZIONE DIMOSTRARE SE SONO VALIDE LE SEGUENTI:



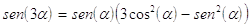
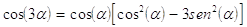
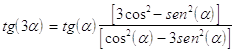
a) è valida solo la prima
b) è valida solo la seconda
c) è valida solo la terza
d) sono tutte valide

 

 

 Formule di bisezione

 

33. USANDO LE FORMULE DI BISEZIONE CALCOLARE IL VALORE  ESATTO DI :   ,   ,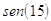   
a)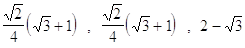
b)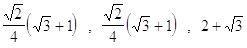
c)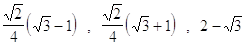
d)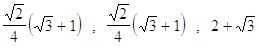

 

Formule parametriche, Formule di prostaferesi

Formule di Werner
Identità goniometriche
Equazioni goniometriche elementari in seno, coseno e tangente.

34. INDICARE LA CORRETTA SOLUZIONE DELLA SEGUENTE EQUAZIONE ELEMENTARE: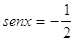
a)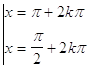    

b)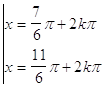

c)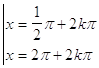

d)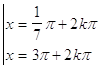
dove k è un numero intero  positivo, negativo o nullo.

 

 

 

35. INDICARE LA CORRETTA SOLUZIONE DELLA SEGUENTE EQUAZIONE ELEMENTARE: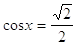
a)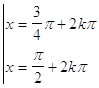
b)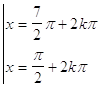
c)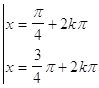
d)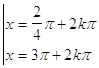
dove k è un numero intero  positivo, negativo o nullo.

36. INDICARE LA CORRETTA SOLUZIONE DELLA SEGUENTE EQUAZIONE ELEMENTARE: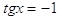

a)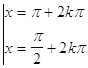

b)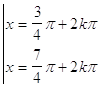

c)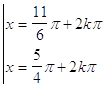
d)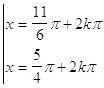
dove k è un numero intero  positivo, negativo o nullo.

37. INDICARE LA CORRETTA SOLUZIONE DELLA SEGUENTE EQUAZIONE ELEMENTARE: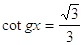 
a)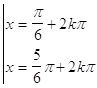

b)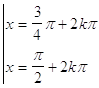

c)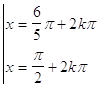
d)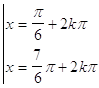
dove k è un numero intero  positivo, negativo o nullo.

 

Disequazioni goniometriche elementari

 

38. INDICARE PER QUALI VALORI DELL’ANGOLO a È SODDISFATTA LA SEGUENTE DISEQUAZIONE GONIOMETRICA: 
a)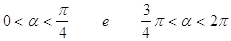
b)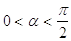
c)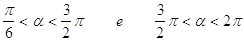
d)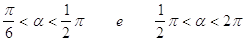

 

 

 

 

 

39. INDICARE PER QUALI VALORI DELL’ANGOLO a È SODDISFATTA LA SEGUENTE DISEQUAZIONE GONIOMETRICA: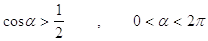
a)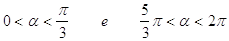
b)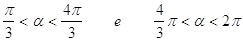
c)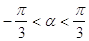
d)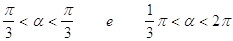

40. INDICARE PER QUALI VALORI DELL’ANGOLO a È SODDISFATTA LA SEGUENTE DISEQUAZIONE GONIOMETRICA: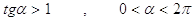
a)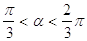
b)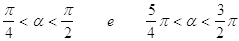
c)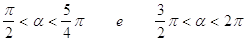
d)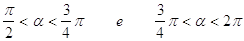

41. INDICARE PER QUALI VALORI DELL’ANGOLO a È SODDISFATTA LA SEGUENTE DISEQUAZIONE GONIOMETRICA:
a)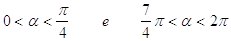  
b)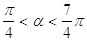
c)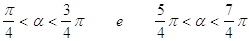
d)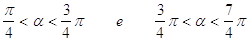
*sono esplementari quegli archi la cui somma è una circonferenza.

 

 

 

 

 

 

II . TRIGONOMETRIA PIANA

 

Teoremi sui triangoli rettangoli

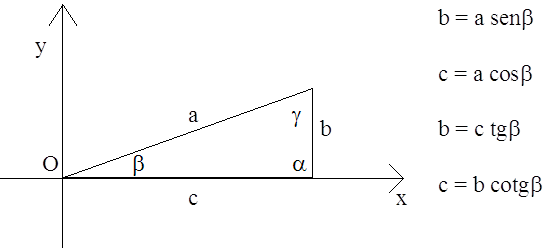
facendo riferimento alla figura rispondere ai seguenti quesiti:

42. DATI I CATETI b, c , INDICARE QUAL È LA GIUSTA FORMULA CHE DETERMINA b.
a)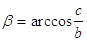
b)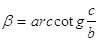
c)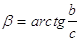
d)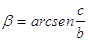

43. DATI I CATETI b , c , INDICARE QUAL È LA GIUSTA FORMULA CHE DETERMINA L’IPOTENUSA a :
a)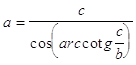
b)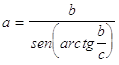
c)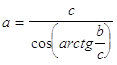
d)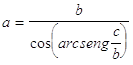

 

 

 

44. DATI L’IPOTENUSA a E UN CATETO b , INDICARE QUAL È LA GIUSTA FORMULA CHE DETERMINA g.
a)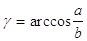
b)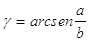
c)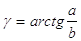
d)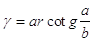

45. SIA b = 1 , b= 45°, USANDO I TEOREMI SUI TRIANGOLI RETTANGOLO ,  INDICARE QUAL È IL CORRETTO VALORE DELL’IPOTENUSA a.
a) 3
b)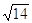
c)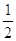
d)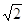

46. SIA b = 2 , g= 45°, USANDO I TEOREMI SUI TRIANGOLI RETTANGOLI ,  INDICARE QUAL È IL CORRETTO VALORE DELL’IPOTENUSA a.
a)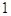
b)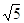
c)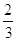
d) 2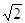

47. SIA b = 2 , b= 60°, USANDO I TEOREMI SUI TRIANGOLI RETTANGOLO ,  INDICARE QUAL È IL CORRETTO VALORE DEL CATETO c.
a)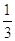
b)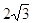
c)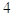
d) 0

48. SIA b = 2 , E a = 4 USANDO I TEOREMI SUI TRIANGOLI RETTANGOLI E LE FORMULE TRIGONOMETRICHE INVERSE , INDICARE IL CORRETTO VALORE DI  b.
a)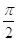
b)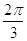
c)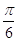

 

 

49. SIA b = 3Ö3, E  c = 9 USANDO I TEOREMI SUI TRIANGOLI RETTANGOLI E LE FORMULE TRIGONOMETRICHE INVERSE , INDICARE IL CORRETTO VALORE DI b.
a)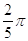
b)
c)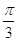
d)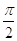

50. SIA a = 4 , g = 60° USANDO I TEOREMI SUI TRIANGOLI RETTANGOLI ,  INDICARE QUAL È IL CORRETTO VALORE DEL CATETO c:
a)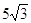
b)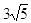
c)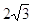
d) 1

 

Teoremi sui triangoli qualunque

 

Teorema della corda:

Teorema dei seni (o di Eulero):

 

 

 

 

 

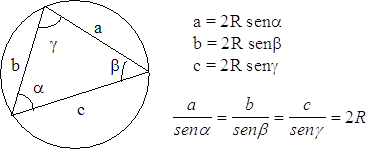
Teorema del coseno (o di Carnot):

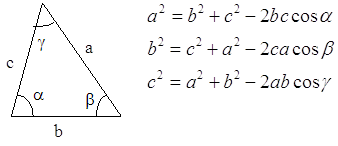
51. CALCOLARE LA CORDA DELLA CIRCONFERENZA DI RAGGIO R = 3CM E ANGOLO ALLA CIRCONFERENZA  a = 30°
a) 3cm
b) 5cm
c) 6sen (30°)  cm
d) 2cm

 

52. CALCOLARE IL RAGGIO R DELLA CIRCONFERENZA SAPENDO IL VALORE DI UNA SUA CORDA ( AC = 4CM ), E L’ANGOLO CHE INSISTE SULL’ARCO MINORE SOTTESO DALLA CORDA STESSA (a = 45°):
a) 4 cm
b) 2Ö2 cm­
c)­ 5 cm
d) 2 cm
­
53. UN TRIANGOLO ISCRITTO IN UNA CIRCONFERENZA DI RAGGIO R = 6CM , HA I TRE ANGOLI DI 60°, INDICARE QUAL È IL CORRETTO VALORE DEI SUOI LATI :
a) a = 3cm, b = 5cm , c = 3cm
b) ­­a = 3cm, b = 3cm , c = 3cm
c) a = 3Ö3cm, b = 3Ö3cm,c = 3Ö3cm
d) a = 2 cm, b = 2 cm , c = 4 cm

54. DI UN TRIANGOLO QUALUNQUE SI CONOSCONO UN LATO (a = 16 cm), L’ANGOLO OPPOSTO A TALE LATO (a= 45°) E UN ALTRO ANGOLO (b=30°) DIRE QUAL È IL VALORE DEL LATO OPPOSTO A b (b) :
a) 16 cm
b) 2Ö2cm
c) 15 cm
d) 8Ö2cm

55.I DUE LATI DI UN TRIANGOLO SONO LUNGHI RISPETTIVAMENTE b = 5 CM , c = 3 CM E L’ANGOLO COMPRESO TRA ESSI VALE  a= 120°, DETERMINARE IL VALORE DEL LATO a :
a) 8cm
b) 7cm
c) 9cm

 

 

56.I TRE LATI DI UN TRIANGOLO SONO LUNGHI RISPETTIVAMENTE a = 5CM , b = 4CM , C = 3CM , INDICARE QUAL È IL CORRETTO VALORE DELL’ANGOLO OPPOSTO AL LATO a (a)  E DI CHE TRIANGOLO SI TRATTA:
a) a= 45°  , triangolo rettangolo
b) a= 60°  , triangolo isoscele
c) a= 90°  , triangolo rettangolo
c) a= 30°  , triangolo isoscele

 

III. GEOMETRIA

 

57. UN PIANO PUÒ ESSERE INDIVIDUATO DA
a)  una retta e da un punto esterno ad essa.
b)  due rette incidenti.
c) sia  a) che b).
d)  quattro punti non allineati.

58. DUE RETTE SGHEMBE SI DIFFERENZIANO DA DUE RETTE PARALLELE PERCHÈ  
a) sono incidenti.
b) non sono complanari.
c) sono perpendicolari.
d) non c’è nessuna differenza.

59. SIA r UNA RETTA NON PERPENDICOLARE AD UN PIANO a, QUANTI PIANI PASSANTI PER LA RETTA r SONO PERPENDICOLARI AD a?
a) Infiniti, perché r genera un fascio infinito di  piani.
b) Due, quello soprastante e quello sottostante ad a.
c) Esiste un solo piano passante per r e perpendicolare ad  a.
d) Non è detto che esista un piano per r perpendicolare ad a.

60. SIA p  UN PIANO CHE INTERSECA DUE PIANI PARALLELI a, b;  ALLORA
a) le rette di intersezione a e b  sono sghembe.
b) i due punti di intersezione sono allineati.
c) le rette a e b di intersezione sono parallele.
d)una retta qualsiasi r di p  è perpendicolare ai due piani a, e b.

61. DATE TRE RETTE PASSANTI PER UNO STESSO PUNTO E NON GIACENTI SU UNO STESSO PIANO, SE SI CONSIDERANO I TRE PIANI RISPETTIVAMENTE PERPENDICOLARI AD ESSE SI HA
a) nessun punto in comune.
b) un solo punto in comune.
c) una retta in comune.
d) un piano in comune.

 

 

 

 

62. SE ESISTE, QUAL È LA DIFFERENZA TRA UN DIEDRO ED UN ANGOLOIDE?
a) Tra diedro e angoloide non c’è nessuna differenza sono entrambe porzioni di spazio limitate da piani consecutivi.
b) Un diedro è un sottomultiplo di un angoloide.
c) Un angoloide è un sottomultiplo di un diedro.
d) Un diedro è costituito da due semipiani aventi in comune la stessa origine mentre l’angoloide è costituito da un fascio di rette aventi la stessa origine e tali che ogni piano delimitato da due rette consecutive lasci le altre tutte da una stessa parte, pertanto un diedro può essere concavo mentre un angoloide no.

63. UNA PIRAMIDE SI DEFINISCE REGOLARE QUANDO
a) la base è un triangolo equilatero.
b) la base è formata da un poligono inscrivibile in un cerchio.
c) le facce laterali sono triangoli equilateri.
d) la base è formata da un poligono regolare circoscrivibile ad un cerchio.

64. IL PIANO TANGENTE AD UNA SUPERFICIE CILINDRICA INDEFINITA IN UNA SUA  GENERATRICE È
a) il piano perpendicolare al piano determinato dall’asse e dalla generatrice. 
b) il piano parallelo al piano determinato dall’asse e dalla generatrice.
c) il piano contenente l’asse.
d) il piano contenente la generatrice e il raggio di base.

65. QUANDO UN CILINDRO SI DICE EQUILATERO
a) quando l’area laterale è equivalente all’area della base.
b) quando l’altezza è uguale al diametro h=d.
c) quando l’area laterale è equivalente alla metà dell’area totale.
d) i cilindri non sono equilateri perchè non hanno lati.

66. QUANDO UNA PIRAMIDE PUÒ ESSERE DEFINITA CONCAVA
a) quando è concavo il poligono di base.
b)una piramide non è mai concava.
c)una piramide è sempre concava.
d) quando la piramide non è retta.

67. LE DIAGONALI DI UN PRISMA RETTO SONO UGUALI
a) si sono uguali e lo dividono in parti uguali.
b) sono uguali solo quando il poligono di base è regolare.
c) sono uguali solo nei parallelepipedi.
d) sono uguali solo nei parallelepipedi rettangoli.

68. QUAL È LA RELAZIONE CHE LEGA, L’ALTEZZA h, L’APOTEMA a ED IL RAGGIO r DEL CERCHIO INSCRITTO AL POLIGONO DI BASE DI UNA PIRAMIDE?
a) r2 = h2 + a2
b)h2 = r2 + a2
c) a2 = h2 + r2
d)a2=h r

 

 

69. SE F È IL NUMERO DELLE FACCE DI UN POLIEDRO REGOLARE, S È IL NUMERO DEGLI SPIGOLI E V IL VOLUME QUALE È LA RELAZIONE CHE LI LEGA?
a) la formula di Eulero F+S = V+2
b) la formula di Keplero F +2=V+S
-c)la formula di Eulero F+V = S+2
d) la formula di Euclide F+V = 2S

70. COME SI DETERMINA L’APOTEMA a DI UN TRONCO DI CONO DI ALTEZZA h E RAGGI DI BASE r ED r’?
a) a =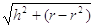
b) a =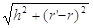
c) a =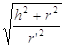
d) a =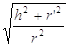

71. COSA AFFERMA IL PRINCIPIO DI CAVALIERI?
a) Fornisce una condizione necessaria e sufficiente di equivalezza tra due solidi.
b) Che, se ogni piano parallelo ad un piano fisso, taglia due solidi formando figure piane equivalenti, allora i solidi sono equivalenti.
c)  Che, se esiste almeno un piano che tagliando due o più solidi forma figure piane equivalenti allora i solidi sono equivalenti.
d) Sono valide sia a) che b).

72. QUANTI ASSI DI SIMMETRIA HA UN CUBO?
a) 6 assi che uniscono gli spigoli opposti.
b) Infiniti, perché per il centro passano infinite rette.
c) 3 assi passanti per il centro delle facce opposte.
d) 9 assi (3 formati dalle rette che uniscono i centri delle facce opposte e 6 dalle rette che uniscono i punti medi degli spigoli opposti.

73. QUANTI PIANI DI SIMMETRIA HA UN TETRAEDRO?
a) 6 piani, ognuno passante per uno spigolo e per il punto medio dello spigolo opposto.
b) 3 rette passanti per i vertici.
c) 1 piano parallelo alla base che ha per centro il vertice del tetraedro.
d) Nessuno.

74. SI CHIAMA SEGMENTO SFERICO A DUE BASI
a) la parte di sfera compresa tra due piani secanti paralleli.
b) ciascuna delle parti solide in cui la sfera è divisa da un piano secante.
c) la parte di sfera generata da un settore circolare.
d) la parte di superficie sferica limitata da due semipiani diametrali.

 

 

 

75. SIA DATA UNA SFERA DI RAGGIO r QUALUNQUE,  QUALE ALTRO SOLIDO HA IL SUO STESSO VOLUME?
a)  In base al principio di Archimede ad un cilindro equilatero di raggio r.
b)  un cono di raggio 2r.
c)  in base al principio di Cavalieri ad un cilindro di raggio 2r.
d) la scodella di Galileo cioè un cilindro, di altezza 2r e raggio r, al quale si è sottratto una semisfera  di raggio r ad esso tangente.

76. IL VOLUME V DI UNO SPICCHIO SFERICO DI ANGOLO a OTTENUTO DA UNA SFERA DI RAGGIO R SI RICAVA DA
a) V: volsfera  = a : 360°.
b) V = 360° volsfera/ a.
c) V = p r2 a/270.
d) V = 4pr3/3.

 

Griglia delle risposte esatte

 

Test n°	Risposta esatta
1	a
2	d
3	b
4	a
5	c
6	d
7	a
8	d
9	a
10	c
11	a
12	b,c
13	b
14	d
15	a,d
16	c
17	d
18	a,b
19	b,c
20	a,c
21	c
22	c
23	a
24	d
25	b
26	b
27	a
28	c
29	d
30	a
31	c
32	d
33	c
34	b
35	c
36	b
37	d
38	a
39	a,c
40	b
41	a
42	b,c
43	a,b,c
44	a
45	d
46	d
47	b
48	c
49	b,c
50	c
51	a,c
52	b
53	c
54	b
55	d
56	c
57	c
58	b
59	c
60	c
61	b
62	d
63	d
64	a
65	b
66	a
67	d
68	c
69	c
70	a
71	b
72	d
73	a
74	a
75	d
76	a

 

Fonte: http://www.liceodanilodolci.it/files/public/Pagano/archivio%20domande/MATEMATICA.DOC

 

Autore del testo: non indicato nel documento di origine

 

 

 

Matematica domande e risposte

 

 

Matematica domande e risposte

 

Disclaimer

Questo sito non rappresenta una testata giornalistica e viene aggiornato senza alcuna periodicità, esclusivamente sulla base della disponibilità del materiale, pertanto non è un prodotto editoriale sottoposto alla disciplina di cui all'art. 1, comma III della Legge n. 62 del 7.03.2001. I riassunti , gli appunti i testi e le citazioni contenuti nel nostro sito sono messi a disposizione gratuitamente a studenti, ricercatori, professori, tecnici con scopi illustrativi didattici e scientifici con il concetto del fair use e con obiettivo del rispetto della direttiva europea 2001/29/CE e della legge n. 633 art. 70 e dlg 68. Il sito è curato e coordinato dall’autore al solo scopo informativo e didattico. Pur ritenendo le fonti utilizzate affidabili, l'autore di questo sito non garantisce l'accuratezza e l'integrità delle informazioni contenute e pertanto declina ogni responsabilità per eventuali problemi o danni causati da errori o omissioni, nel caso tali errori o omissioni risultino da negligenza, caso fortuito o altra causa. Tutti gli appunti, le citazioni i testi e le immagini , sono proprietà dei rispettivi autori o case di produzione che ne detengono i diritti, qualora gli aventi diritto si ritenessero danneggiati dall'inserimento in questo sito dei predetti files o fossero stati inavvertitamente inseriti immagini, informazioni, testi od altro materiale coperto da Copyright saranno immediatamente rimossi e/o ne saranno citate le fonti su semplice segnalazione all' indirizzo e-mail indicato nella pagina contatti .

Gli obiettivi di questo sito sono il progresso delle scienze e delle arti utili in quanto pensiamo che siano molto importanti per il nostro paese i benefici sociali e culturali della libera diffusione di informazioni utili. Tutte le informazioni e le immagini contenute in questo sito vengono qui utilizzate esclusivamente a scopi didattici, conoscitivi e divulgativi. Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione). In questo sito abbiamo fatto ogni sforzo per garantire l'accuratezza dei tools, calcolatori e delle informazioni, non possiamo dare una garanzia o essere ritenuti responsabili per eventuali errori che sono stati fatti, i testi utilizzati sono stati prelevati da siti che li hanno messi a disposizione gratuitamente per farli conoscere nel web con scopi didattici. Se trovate un errore su questo sito o se trovate un testo o tool che possa violare le leggi vigenti in materia di diritti di autore, comunicatecelo via e-mail e noi provvederemo tempestivamente a rimuoverlo.

 

---

 

---

 

Designed by Larapedia.com 1998 -2011