Descartes e Fermat sulla tangente alla cicloide

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Descartes e Fermat sulla tangente alla cicloide

Descartes e Fermat sulla tangente alla cicloide.

Lo studio della cicloide occupò quasi tutti i matematici della prima metà del Seicento. Roberval e Torricelli ne determinarono l’area, Pascal trovò una quantità di risultati: centro di gravità, volumi e centri di gravità dei solidi ottenuti ruotandola attorno alla base e all’asse. Sempre Roberval trovò la tangente alla cicloide utilizzando la sua generazione come composizione di due movimenti.

Anche Descartes e Fermat risolsero il problema della tangente alla cicloide, anche se con due metodi completamente differenti. Fermat lo vide come un banco di prova del suo metodo di adequazione nella sua massima generalità, dunque in definitiva lo inquadrò in un metodo generale di tracciamento delle tangenti alle curve sia algebriche che trascendenti. Al contrario Descartes, il cui metodo –come abbiamo visto– si applicava solo alle curve algebriche, escogitò un ragionamento ad hoc, valido è vero per la sola cicloide, ma estrememente brillante e conciso.

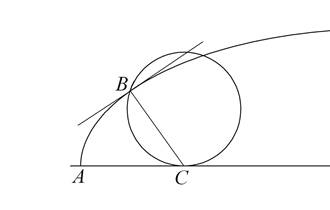
L’idea centrale di Descartes si basa sul fatto che il cerchio generatore della cicloide rotola senza strisciare sulla retta AC; dunque ad ogni istante il punto C, in cui il cerchio generatore tocca la retta AC, è immobile e il moto si riduce a una rotazione attorno a C.

Di conseguenza la retta CB, che unisce il centro isatntaneo di rotazione C al punto B sulla cicloide, è ortogonale alla cicloide; la perpendicolare a CB per B sarà allora la tangente cercata.

Al contrario di descartes, Fermat trova la tangente alla cicloide applicando il suo metodo dell’adequazione, che consiste nello scrivere la proprietà caratteristica della curva in esame sui punti della tangente. Per prima cosa dunque, occorrerà trovare la proprietà caratteristica della cicloide. Fermat considera la (semi)-cicloide FBA e il (semi)-cerchio generatore ADE. Preso un punto qualsiasi C sul diametro, si traccia la retta orizzontale CB che incontra la cicloide in B.

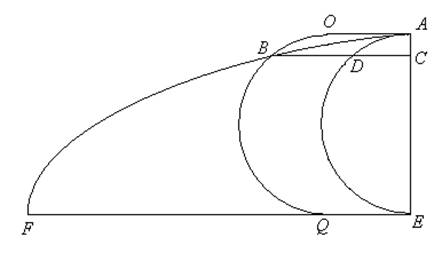
Immaginiamo ora di spostare il semicerchio ADE fino a farlo passare per B; per la proprietà della cicloide l’arco BQ sarà uguale al segmento FQ. Poiché l’intero segmento FE è uguale alla semicirconferenza ADE, e l’arco BQ è uguaale all’arco DE, il segmento QE sarà uguale all’arco AD. D’altra parte i segmenti BD e QE sono uguali, e quindi in definitiva il segmento BD è uguale all’arco AD. In conclusione, se si prende un qualsiasi punto C sul diametro e si tira la retta CB che incontra la circonferenza in D e la cicloide in B, l’arco AD è uguale al segmento BD compreso tra la circonferenza e la cicloide. Questa è la proprietà caratteristica da cui Fermat parte per determinare la tangente alla cicloide nel punto B.

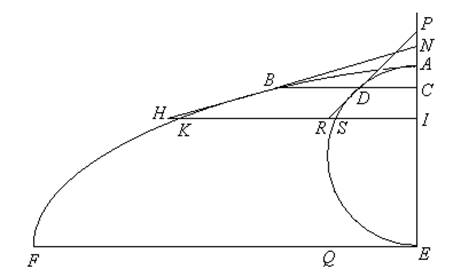
Una volta individuata la proprietà caratteristica, tracciamo le tangenti alla circonferenza e alla cicloide nei punti corrispondenti D e B; la prima sarà nota (in particolare sarà dteerminato il punto P in cui incontra l’asse, la seconda incognita. Per determinarla, bisogna trovare il punto N, ossia la lunghezza del segmento CN.

Nella figura a fianco, i segmenti AC=b, BC=c, PC=d, PD=f, BD=g, DC=h saranno quantità note , mentre l’incognita è la lunghezza del segmento CN=a (seguendo Fermat, che usa le notazioni di Viète, indichiamo con le consonanti le quantità note e con le vocali le incognite). Prendiamo ora un punto H sulla tangente, e tirata la retta HI indichiamo con K, R e S le sue intersezioni con la cicloide, con la tangente alla circonferenza e con la circonferenza. Poniamo poi CI=e .

Per la similitudine dei triangoli HNI e BCN si ha HI:BC=NI:NC, e dunque

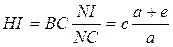Per applicare ora il metodo di fermat, bisogna scrivere la proprietà caratteristica della cicloide relativamente al punto H sulla tangente. Si può anche prendere il punto R sulla tangente alla circonferenza, e scrivere HR al posto di KS. Avremo allora

HR ≈ arco AS = arco AD + arco DS = BD + arco DS.

A questo punto entra un’altra caratteristica essenziale del metodo di Fermat, quella che ne consente l’applicazione anche alle curve trascendenti come la cicloide. Dice Fermat:

se si vuole si possono prendere le ordinate sulle tangenti trovate col metodo precedente al posto di quelle sulle curve; e inoltre (e questo è il pregio del metodo) si possono prendere porzioni delle tangenti già trovate al posto delle porzioni corrispondenti delle curve, in modo da trovare l'adequazione.

Nel nostro caso, si può sostituire l’arco DS con la porzione DR della tangente. Avremo dunque

HR ≈ BD + DR.

Si tratta ora di esprimere HR e DR in termini delle grandezze date. Per la similitudine dei triangoli PRI e PDC si ha DR:CI=PD:PC, e dunque

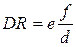Quanto al primo membro, risulta HR = HI – RI, e per la similitudine dei triangoli PRI e PDC avremo RI:DC=PI:PC, da cui .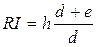

Si ha dunque in conclusione:

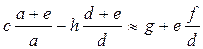Sviluppando e ricordando che c=g+h, troviamo

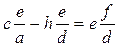
e quindi in conclusione

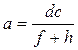Si suppone qui che sia nota la tangente alla circonferenza, che comunque può essere trovata con il metodo di Fermat (può essere un utile esercizio). Naturalmente le varie grandezze non sono indipendenti (ad esempio si ha c=g+h e f²=d²+h²); noi abbiamo usato una lettera diversa per ognuna per non appesantire le notazioni.

Se il punto K si trova tra B e N, la quantità e sarà negativa.

Fonte: http://univaq.it/~leonetti/ssis/schede/05_Descartes_e_Fermat_sulla_tangente_alla_cicloide.doc

Sito web da visitare: http://univaq.it/~leonetti/

Autore del testo: non indicato nel documento di origine

Nota : se siete l'autore del testo sopra indicato inviateci un e-mail con i vostri dati , dopo le opportune verifiche inseriremo i vostri dati o in base alla vostra eventuale richiesta rimuoveremo il testo.

Parola chiave google : Descartes e Fermat sulla tangente alla cicloide tipo file : doc

Descartes e Fermat sulla tangente alla cicloide