Angolo solido

 

 

Angolo solido

 

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

 

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

 

 

 

 

Angolo solido

 

Angolo solido
La nozione di angolo solido costituisce una estensione, la più generale, del concetto di angolo nel piano.
L'angolo definito nel piano  è una delle due regioni delimitate da due semirette aventi la stessa origine; se andiamo però ad analizzare sia lo sviluppo del concetto di angolo da un punto di vista storico, sia alcune situazioni notevoli come l'angolo giro, l'angolo nullo, ecc.  appare chiaro come questa definizione sia a volte inadeguata a chiarire tutti gli aspetti del concetto di angolo. Ad esempio, il dinamismo di una semiretta che ruota nel piano intorno ad un'altra avente la stessa origine, occupando tutte le posizioni successive di varie semirette uscenti da uno stesso punto, fino a tornare a coincidere con quella fissata dopo una rotazione completa, induce molto meglio la comprensione di che cosa sia un angolo giro e un angolo nullo (rotazione di angolo nullo). Ci troviamo quindi di fronte ad un tipo di definizione (quella data all'inizio), che è di tipo dichiarativo, ma che necessita didatticamente di altre definizioni, complementari o alternative ad essa, perché sia adeguatamente chiara ed esaustiva. A riguardo, come esemplificato, è importante un approccio costruttivo alla definizione di angolo.
Questo tipo di approccio viene ripreso necessariamente quando nasce l'esigenza di trasferire il concetto di angolo in ambito tridimensionale. Qui appare chiaro che un'unica definizione non è sufficiente: si possono individuare più configurazioni nello spazio che ci riconducono per analogia al concetto di angolo nel piano.
La prima situazione, più immediata, è quella di sostituire alle due semirette uscenti dallo stesso punto due semipiani uscenti da una stessa retta (angolo diedro) : per classificare però gli angoli così definiti sulla scia della classificazione degli angoli nel piano è necessario considerare la sezione normale di un diedro con un piano, ottenuta considerando l'insieme dei punti del diedro comuni ad un piano perpendicolare alla retta di origine del diedro stesso. Si potrà così parlare di diedro retto, e definire anche la misura dell'ampiezza dell'angolo diedro, riconducendo tale ampiezza a quella della sezione, che è un angolo nel piano.

La nozione di angolo diedro, pur essendo la più diffusa, non esaurisce però tutte le situazioni geometriche in cui nello spazio si individua una regione che è analoga all'angolo definito nel piano. La stessa natura ci presenta moltissime forme poliedriche, in cui non sono solo due piani uscenti da una stessa retta, ma più superfici piane uscenti da un medesimo punto a delimitare una regione solida.  A tale scopo è necessaria la nozione di angoloide, per il quale  la definizione ha un approccio decisamente costruttivo:  si conducono da un punto esterno ad un poligono  convesso semirette che incontrino i punti del  contorno di tale poligono: esse individuano a due a due parti di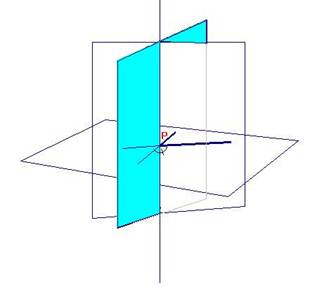

 
a due a due parti di superfici piane, che delimitano, internamente ed esternamente, due regioni dello spazio: quella interna è detta angoloide. Si noti che in questo caso siamo di fronte ad una ulteriore generalizzazione del concetto di angolo nel piano trasferito nello spazio tridimensionale: dalle due semirette uscenti dalla stessa origine si passa a più semirette uscenti dallo stesso punto, e a superfici piane che delimitano l'angoloide, ognuna delle quali riporta alla configurazione di angolo nel piano. La sezione di un angoloide con un piano non passante per il suo vertice è ovviamente un poligono convesso (non necessariamente congruente a quello che ha definito l'angoloide).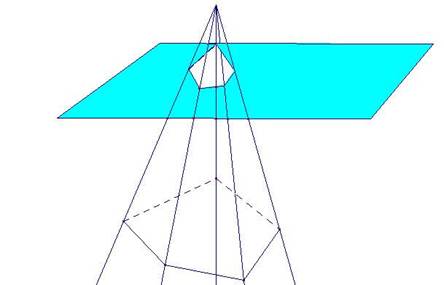

Tuttavia, anche con la nozione di angoloide avvertiamo una certa inadeguatezza a descrivere gli angoli nello spazio.
Già nella cultura greca classica troviamo testimoniata l'esigenza (Proclo, Euclide, Apollonio,..) di estendere l'idea di angolo anche a figure, nel piano stesso, di contorni mistilinei e curvilinei, oltre che rettilinei.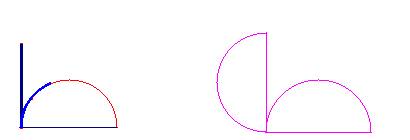

       (esempi di angoli curvilineo e  lunulare )
Tale esigenza di generalizzazione ulteriore (che si scontrava comunque nella cultura antica con gli inevitabili problemi connessi con la misura), testimonia la necessità di definire rigorosamente situazioni, soprattutto tridimensionali, in cui la superficie che delimita la regione non sia solo piana o unione di superfici piane, ma sia una superficie rotonda.
Si perviene così alla nozione di angolo solido, che costituisce la maggiore generalizzazione di questo concetto nello spazio:  l'angolo solido è delimitato da  rette che sono le generatrici di un cono nello spazio.
La sua sezione con un piano non passante per il vertice dell'angolo solido è una figura chiusa di contorno curvilineo.

La definizione può essere data nel seguente modo:
si dice angolo solido ciascuna delle due regioni in cui viene suddiviso lo spazio della superficie conica formata dalle  semirette passanti per uno stesso punto (detto vertice dell'angolo solido) e per i punti di una curva chiusa semplice tracciata su di una superficie non contenente il vertice.  Si noti l'analogia con la definizione di angoloide, in cui le semirette uscenti da uno stesso punto incontravano il contorno di un poligono, quindi una linea spezzata, piuttosto che una curva.

 
Si pone poi il problema di definire l'ampiezza di un angolo solido e la sua misura, visto che in tal caso non ci può ricondurre, come per il diedro e l'angoloide, attraverso la sezione, all'ampiezza di angoli piani.
Si definisce  steradiante l'unità di misura degli angoli solidi. Esso corrisponde ad un angolo solido "unitario"(sterangolo), delimitato da un cono che interseca una sfera. Lo sterangolo corrisponde all'angolo solido sotto il quale si vede, dal centro di una sfera di dato raggio, una porzione di superficie sferica pari al quadrato del raggio.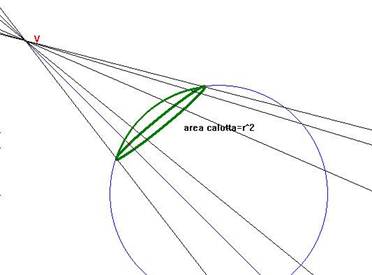

La misura di uno sterangolo è data dal rapporto tra l'area della superficie che esso interseca  su una sfera avente centro nel suo vertice ed il quadrato del raggio di tale sfera, rapporto che non cambia al mutare del raggio della sfera.

 

Fonte: http://www.deambrosisnatta.org/files/angolo_solido.doc

Sito web da visitare: http://www.deambrosisnatta.org

Autore del testo: non indicato nel documento di origine

Parola chiave google : Angolo solido tipo file : doc

 

 

 

 

Visita la nostra pagina principale

 

Angolo solido

 

Termini d' uso e privacy

 

 

 

 

Angolo solido