Archimede misura del cerchio

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Archimede misura del cerchio

Archimede, Misura del cerchio.

1. Ogni cerchio è equivalente a un triangolo rettangolo in cui l’altezza è uguale al raggio del cerchio e la base alla circonferenza.

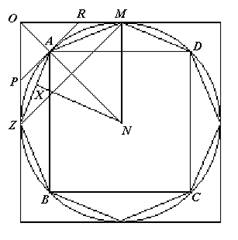
Sia ABCD un cerchio e E un triangolo come detto; dico che sono equivalenti.

Supponiamo per assurdo che il cerchio sia più grande del triangolo. Inscriviamo nel cerchio il quadrato AC e dividiamo gli archi [che hanno come corde i lati del quadrato] in due parti uguali; (a) continuiamo la divisione finché la somma dei segmenti del cerchio sia minore della differenza tra l’area del cerchio e quella del triangolo. (b) Il poligono inscritto sarà allora maggiore del triangolo.

Prendiamo il centro N e abbassiamo la perpendicolare NX, che sarà minore dell’altezza del triangolo. Ma anche il perimetro del poligono è a sua volta minore della base, dato che è minore della circonferenza del cerchio. Di conseguenza, il poligono è minore del triangolo E, il che è assurdo.

Sempre ragionando per assurdo, supponiamo ora che il cerchio sia più piccolo del triangolo E, circoscriviamogli un quadrato, dividiamo gli archi in due parti uguali e tiriamo le tangenti ai punti di divisione. L’angolo OAR è retto, e quindi OR è maggiore di MR, dato che MR è uguale a RA, e il triangolo ROP è maggiore della metà della figura OZAM. (c) Restino dunque dei segmenti come PZA, la cui somma sia minore della differenza tra l’area del triangolo E e quella del cerchio ABCD. Il poligono circoscritto è di conseguenza minore del triangolo E, il che è assurdo. (d) Infatti è maggiore, dato che NA è uguale all’altezza del triangolo e che il perimetro del poligono è maggiore della base del triangolo.

Pertanto il cerchio è equivalente al triangolo E.

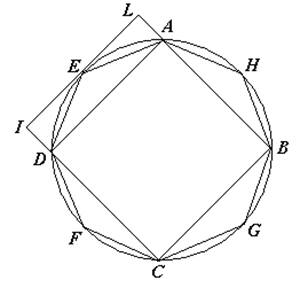
(a) Euclide, Elementi, XII.2

Il quadrato inscritto è maggiore della metà del cerchio; infatti è uguale alla metà del quadrato circoscritto.

Si dividano ora a metà gli archi che hanno come corde i lati del quadrato inscritto. Il triangolo AED è maggiore della metà del segmento corrispondente; infatti è metà del rettangolo ADIL. Di conseguenza la somma dei triangoli è maggiore della metà della somma dei segmenti corrispondenti.

Si possono ora inscrivere dei triangoli nei segmenti residui, e così via; ogni volta la somma dei triangoli è maggiore della metà della somma dei segmenti corrispondenti. Pertanto togliendo ogni volta i triangoli costruiti, si toglie sempre una grandezza maggiore della metà del residuo.

Si può allora applicare il teorema X.1 degli Elementi: Date due grandezze, se dalla prima si toglie più della metà, e dal residuo si toglie ancora più della metà, e così via, a un certo punto il residuo sarà minore della seconda grandezza data.

Nel nostro caso, la prima grandezza è il cerchio e la seconda l’ipotetica differenza tra l’area del cerchio e quella del triangolo. Le grandezze che si tolgono formano i poligoni inscritti.

(b) Infatti il cerchio meno il poligono, che è uguale alla somma dei segmenti, è minore della differenza tra il cerchio e il triangolo. Di conseguenza il poligono è minore del triangolo.

(c) Si può fare ogni volta la stessa costruzione; ad esempio nel triangolo ARM, tirando la tangente al punto di mezzo dell’arco. Ogni volta il triangolo esterno al cerchio è maggiore della metà della figura relativa. Partendo ora dal quadrato circoscritto e togliendo ogni volta i triangoli detti, si ottengono i vari poligoni circoscritti; la differenza tra questi e il cerchio finirà col diventare minore di una qualsiasi grandezza data, nel nostro caso l’ipotatica differenza tra il triangolo E e il cerchio.

(d) Che il perimetro di un qualsiasi poligono circoscritto sia maggiore della circonferenza (e quindi della base del triangolo) segue dal postulato 2 del primo libro della Sfera e cilindro di Archimede: Se due linee hanno gli stessi estremi e sono convesse, e se la prima di esse è compresa tra la seconda e la retta che ha gli stessi estremi, allora la prima è più corta della seconda. Nel nostro caso le due linee sono l’arco AM e la spezzata ARM: l’arco è più corto della spezzata e di conseguenza la circonferenza è minore del perimetro del poligono circoscritto.

Fonte: http://univaq.it/~leonetti/ssis/schede/01_Archimede_misura_del_cerchio.doc

Sito web da visitare: http://univaq.it/

Autore del testo: non indicato nel documento di origine

Nota : se siete l'autore del testo sopra indicato inviateci un e-mail con i vostri dati , dopo le opportune verifiche inseriremo i vostri dati o in base alla vostra eventuale richiesta rimuoveremo il testo.

Archimede misura del cerchio