Geometria razionale misura proporzionalità

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Geometria razionale misura proporzionalità

La misura

Classi di grandezze omogenee

L'obiettivo di questo paragrafo è quello di ottenere un procedimento teorico per misurare alcuni enti geometrici come segmenti, angoli, superifici, solidi. Non è possibile invece misurare punti, rette, semirette.

L'operazione del misurare consiste sostanzialmente nell'assegnare a una grandezza geometrica, ma non solo, un numero ben definito. Questo numero si ottiene dal confronto tra la grandezza da misurare e una grandezza di riferimento, detta campione. Ci interessa confrontare, per stabilire qual è la più grande? Ci può interessare sommare le grandezze?

In generale, gli oggetti che ci circondano hanno delle caratteristiche: lunghezza, peso, forma, altezza, superficie, colore, temperatura, morbidezza... Alcune di queste caratteristiche sono confrontabili tra di loro, per esempio la lunghezza di due segmenti, il peso di due corpi, altre non sono confrontabili. Le grandezze che si possono confrontare si dicono omogenee. Ci sono poi caratteristiche che sono additive, cioè si lasciano addizionare. Queste caratteristiche che hanno la peculiarità di essere confrontabili e sommabili si chiamano grandezze.

Nei capitoli precedenti abbiamo visto come confrontare e sommare segmenti, confrontare e sommare angoli. Vogliamo fare la stessa cosa con gli archi di circonferenza, le superfici e i volumi.

Non possiamo evidentemente confrontare e sommare punti, perché i punti sono tutti congruenti tra di loro e sommando due punti non otteniamo un altro punto ma due punti. Non possiamo confrontare rette perché sono tutte congruenti tra di loro, non possiamo sommarle perché non otterremmo un'altra retta. Non possiamo per esempio sommare due triangoli. Né possiamo confrontare segmenti con angoli perché non sono grandezze omogenee, non sono dello stesso tipo; non possiamo confrontare angoli con superfici perché non sono omogenee tra di loro...

Diamo ora il concetto generale di classe di grandezze.

DEFINIZIONE. Un insieme di grandezze geometriche si dice che forma una classe di grandezze quando:

1) date due qualunque grandezze, è sempre possibile confrontarle, cioè stabilire se sono uguali, o, in caso contrario, quali di esse sia la maggiore e quale la minore;

2) è sempre possibile definire un’operazione di somma tra grandezze, che goda delle proprietà associativa e commutativa.

Le grandezze di una stessa classe si dicono omogenee.

A partire da questa definizione possiamo dare quella di multiplo e sottomultiplo.

DEFINIZIONE. Data una grandezza geometrica A ed un numero naturale n, la grandezza geometrica B si dice multipla di A secondo il numero n se è data dalla somma di n grandezze tutte uguali ad A; scriveremo B =n• A. In questo caso A è definita grandezza sottomultipla di B secondo il numero naturale n; scriviamo .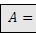

Dato un segmento AB possiamo dare un significato alla scrittura 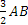nel seguente modo:

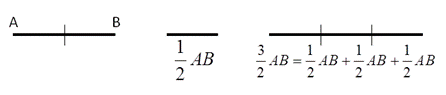Il segmento 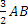è costituito da 3 segmenti ciascuno congruente alla metà di AB.

DEFINIZIONI. Due grandezze omogenee A e B si dicono commensurabili quando esiste una terza grandezza C, ad esse omogenea, che è sottomultipla sia di A che di B: .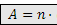

Due grandezze omogenee A e B si dicono incommensurabili quando non esiste una terza grandezza C, ad esse omogenea, che sia sottomultipla sia di A che di B.

L'esistenza di grandezze incommensurabili è confermata dal seguente teorema.

TEOREMA. Il lato e la diagonale di un quadrato sono grandezze incommensurabili.

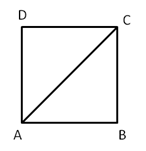. La dimostrazione si sviluppa per assurdo. Con riferimento alla figura, verifichiamo che il lato AB e la diagonale AC del quadrato ABCD sono incommensurabili.

Per assurdo, supponiamo che esista una grandezza U, omogenea sia al lato sia alla diagonale, che sia un sottomultiplo comune, cioè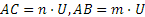

Per il teorema di Pitagora 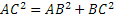C.V.D.

Storicamente, questa è stata la prima scoperta di grandezze incommensurabili, probabilmente dovuta al Ippaso di Metaponto, matematico vissuto tra Crotone e Metaponto (MT) nel 500 a.C. circa. La tradizione dice che morì in un naufragio per aver rivelato la scoperta dell'esistenza delle grandezze incommensurabili, in contrasto con il pensiero del maestro Pitagora.

Siano A e B due grandezze omogonee commensurabili sia C la grandezza sottomultipla in comune, si avrà .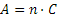

DEFINIZIONE. Si dice rapporto di due grandezze omogenee A e B il numero razionale .

Occorre supporre la validità dei seguenti postulati.

POSTULATO DELLA DIVISIBILITA'. Ogni grandezza geometrica è sempre divisibile in una numero qualunque di parti.

POSTULATO DI EUDOSSO-ARCHIMEDE. Date due grandezze omogenee disuguali esiste sempre una grandezza multipla della minore che supera la maggiore.

Possiamo dare ora la definizione di misura di un segmento rispetto a un altro, nel caso in cui i due segmenti sono commensurabili.

DEFINIZIONE. Date due grandezze A e U commensurabili tra di loro si definisce misura di A rispetto a U il numero razionale , la sua misura rispetto ad U è evidentemente 1.

Solitamente si usa come unità di misura delle lunghezze il metro, con il suo multipli (decametro, ettometro, chilometro, ...) e i suoi sottomultipli (decimentro, centimetro, millimetro, …). Per misurare gli angoli si usa il grado che è dell'angolo giro. Per misurare le superfici si usa come unità di superficie quella di un quadrato di lato 1 m. Per misurare i solidi si usa il volume di un cubo di lato 1m.

Circa la scrittura delle misure, in Italia valgono le seguenti norme: l'unità di misura si scrive sempre dopo il numero che la indica, tranne le misure monetarie: si scrive 12m e non m 12; si scrive € 12 e non 12 €. L'unità di misura non è mai seguita dal puntino, non va mai espressa al plurale.

E' possibile estendere la definizione di rapporto, e la conseguente definizione di misura, anche per la grandezze incommensurabili, come per esempio lato e diagonale dello stesso quadrato. Il percorso però è più lungo e complesso, poiché il rapporto tra due grandezze commensurabili è sempre un numero razionale mentre il rapporto tra due grandezze incommensurabili non è un numero razionale.

Partiamo dalla definizione di classi contigue.

DEFINIZIONE. Due classi di grandezze omogenee (ad esempio, di segmenti) si dicono classi contigue se godono delle seguenti proprietà :

1) sono separate: ogni grandezza della prima classe è minore di ogni grandezza della seconda classe. Vale a questo proposito il postulato della continuità, secondo il quale due classi di grandezze separate ammettono almeno un elemento separatore (ce n’è sicuramente uno, ma potrebbero anche essercene infiniti), cioè una grandezza che sia maggiore (o uguale) di ogni grandezza della prima classe e minore (o uguale) di ogni grandezza della seconda .

2) godono della proprietà dell’avvicinamento indefinito: presa una grandezza ε , piccola a piacere, omogenea a quelle date, esiste sempre una grandezza della seconda classe ed una della prima la cui differenza sia minore di ε.

Per due classi di grandezze contigue vale l’assioma di Cantor: due classi di grandezze contigue ammettono uno e un solo elemento separatore.

Basandoci sul concetto di contiguità possiamo a questo punto definire un qualunque numero irrazionale come l’unico elemento separatore tra due classi contigue di numeri razionali; nella prima classe mettiamo tutti i numeri che approssimano il numero irrazionale per difetto, nella seconda quelli che lo approssimano per eccesso.

Prendendo come esempio il numero irrazionale √2 le due classi sono:

A: 1; 1,4; 1,41; 1,414; 1,4142; ....

B: 2; 1,5; 1,42; 1,415; 1,4143; ...

Si può osservare che le due successioni sono separate, in quanto ogni numero della prima è minore di ogni numero della seconda, inoltre godono della proprietà dell’avvicinamento indefinito, in quanto è sempre possibile trovare un numero razionale appartenente ad A ed uno appartenente a B la cui differenza sia minore di un qualsiasi numero ε, per quanto piccolo questo si prenda.

Quindi, per l’assioma di Cantor, esiste ed è unico l’unico elemento separatore di queste due successioni; possiamo identificare questo numero con la coppia di successioni e scrivere: √2 = (A,B).

Questa definizione vale non solo per i numeri irrazionali, ma anche per i numeri razionali. Per esempio, la frazione 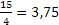è definita dalle classi contigue:

A: 3; 3,7; 3,74; 3,749; 3,7499; ...

B: 4; 3,8; 3,76; 3,751; 3,7501; ...

Possiamo naturalmente definire in questo modo anche i numeri interi. Per esempio 5 è l'elemento separatore delle classi:

A: 4; 4,9; 4,99; 4,999; ...

B: 6; 5,1; 5,01; 5,001; ...

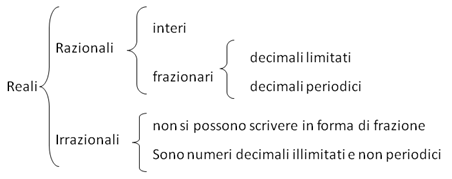
Concludiamo affermando che un qualunque numero reale r può essere definito come l'elemento separatore di una coppia di classi numeriche contigue.

I numeri reali sono quindi il raggruppamento di numero razionali e irrazionali:

Passiamo ora a definire la misura delle grandezze incommensurabili.

Date le lunghezze incommensurabili AB e CD, poniamo

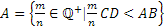
Si dimostra che la coppia (A, B) è una coppia di classi contigue di Q⁺. In maniera intuitiva possiamo dire che A contiene i valori approssimati per difetto e B contiene i valori approssimati per eccesso del rapporto .

Chiamiamo rapporto fra le lunghe incommensurabili AB e CD il numero irrazionale dato dalle classi contigue (A,B).

Vero/falso
Date due grande A e B è sempre possibile confrontarle per stabilire qual è la più grande [V] [F]
Due grandezze geometriche si dicono commensurabili quando esiste una terza grandezza che è sottomultipla comune alle altre due [V] [F]
Un qualunque numero razionale può essere definito come elemento separatore di due classi numeriche contigue [V] [F]
La misura di un segmento è un segmento [V] [F]
la diagonale di un quadrato è incommensurabile [V] [F]
L'insieme delle ampiezze degli angoli rappresenta una classe di grandezze omogenee? Giustifica la risposta.
Disegna un segmento AB a piacere, costruisci poi il segmento .
Qual è il rapporto tra i segmenti AB e CD rappresentati in figura? Indica nel disegno quale può essere l'unità di misura comune ad entrambi.
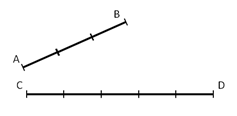Disegna due segmenti AB e CD per i quali valga il rapporto .
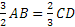E' possibile che due angoli siano tra loro incommensurabili?
E' possibile che i perimetri di due quaadrati siano tra loro incommensurabili? Fai un esempio.
In quali casi le due grandezze A e B sono incommensurabili?

[A]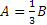

Nel triangolo rettangolo ABC, i cateti AB e AC hanno rapporto , qual è il rapporto tra l'ipotenusa BC e il cateto AB, sono grandezze tra di loro commensurabili?
Dalle relazioni
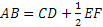
Il segmento AB misura 3a, quanto misura rispetto a ?
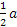Per quale dei seguenti valori di a il numero 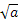è un numero irrazionale?

[A] 1 [B] 2 [C] 3 [D] 4 [E] 5 [F] 6 [G] 8 [H] 9 [I] 10

Proporzionalità tra grandezze

DEFINIZIONE. Date quattro grandezze A,B,C,D, le prime due omogenee tra loro così come le ultime due, queste formano una proporzione se il rapporto delle prime due è uguale al rapporto delle ultime due. Si scrive A : B = C : D e si legge : A sta a B come C sta a D.

Terminologia

Il primo ed il terzo termine (A e C) si chiamano antecedenti.

Il secondo ed il quarto termine (B e D) si chiamano conseguenti.

B e C si chiamano medi.

A e D si chiamano estremi.

La grandezza D si chiama quarta proporzionale.

Se in una proporzione tra grandezze tutte omogenee i medi sono uguali tra loro A : B = B : C, la proporzione si dice continua, e la grandezza B si chiama media proporzionale; la grandezza C si dice terza proporzionale.

TEOREMA FONDAMENTALE. Condizione necessaria e sufficiente affinchè quattro grandezze siano in proporzione è che siano in proporzione le loro misure.

Dimostrazione → (condizione necessaria)

Dimostriamo innanzitutto che la condizione è necessaria: supposto che le quattro grandezze siano in proporzione, dimostriamo che sono in proporzione le loro misure.

Siano A e B due grandezze omogenee, a e b le loro misure rispetto ad un’unità di misura omogenea ad A e B; C e D due grandezze anch’esse omogenee tra loro e c e d le loro misure rispetto ad un’unità di misura omogenea a C e D .

IPOTESI: A : B = C : D

TESI: a : b = c : d

Applicando il teorema secondo cui il rapporto tra due grandezze è uguale al quoziente delle loro misure, avremo: 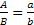che si può anche scrivere nella forma a : b = c : d

Dimostrazione ← (condizione sufficiente)

Dimostriamo ora che la condizione è sufficiente :

IPOTESI: a : b = c : d

TESI: A : B = C : D

Sempre dal teorema citato precedentemente, poiché 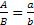, vale a dire A : B = C : D.

_C.V.D.

Ricordiamo che per la proporzionalità tra numeri vale la seguente

PROPRIETA'. Condizione necessaria e sufficiente affinchè quattro numeri siano in proporzione è che il prodotto dei medi sia uguale al prodotto degli estremi.

Proprietà delle proporzioni

Grazie al teorema fondamentale possiamo trasferire le proprietà delle proporzioni tra numeri alle proprozioni tra grandezze.

1. Proprietà dell’invertire

Scambiando ogni antecedente col proprio conseguente otteniamo una nuova proporzione.

Quindi se abbiamo la proporzione A : B = C : D , applicando la proprietà dell'invertire otterremo:

B : A = D : C.

2. Proprietà del permutare

Se le quattro grandezze sono tutte omogenee, possiamo scambiare tra loro i medi o gli estremi, ed otterremo sempre una nuova proporzione.

Quindi dalla proporzione A : B = C : D, applicando la proprietà del permutare otterremo:

A : C = B : D ed anche D : B = C : A

3. Proprietà del comporre

La somma delle prime due grandezze sta alla prima (o alla seconda) grandezza come la somma delle altre due sta alla terza (o alla quarta)

Data dunque la proporzione A : B = C : D, applicando questa proprietà avremo:

(A + B) : A = (C + D) : C oppure anche : (A + B) : B = (C + D) : D

4. Proprietà dello scomporre

La differenza tra la prima e la seconda grandezza sta alla prima (o alla seconda) grandezza come la differenza tra le altre due sta alla terza (o alla quarta). Questa proprietà richiede che ogni antecedente sia maggiore del proprio conseguente.

Se dunque A > B, C > D , avremo che, data la proporzione A : B = C : D, si otterrà:

(A - B) : A = (C - D) : C oppure anche : (A - B) : B = (C - D) : D

In riferimento alla disuguaglianza precedente, va precisato che se quattro grandezze sono in proporzione, tra antecedenti e conseguenti intercorre sempre la stessa relazione, vale a dire che , se la prima grandezza è uguale, maggiore o minore della seconda, anche la terza sarà uguale, maggiore o minore della quarta.

TEOREMA DELLA QUARTA PROPORZIONALE. Date tre grandezze A, B e C, con A e B omogenee tra loro, esiste ed è unica una grandezza D, omogenea alla terza, che con le tre date formi una proporzione.

Dimostrazione

Siano A, B e C tre grandezze, le prime due omogenee tra loro. Supponiamo che esista una quarta grandezza X, omogenea a C, tale che valga la proporzione A : B = C : X.

Sostituendo alle grandezze le loro misure, per il teorema fondamentale dovrà essere a : b = c : x

Applichiamo ora la proprietà fondamentale delle proporzioni numeriche, uguagliando il prodotto dei medi a quello degli estremi ax = bc.

Risolvendo l’equazione in x otteniamo 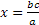, e poiché a, b e c sono diversi da zero (e positivi), in quanto misure di grandezze geometriche, quest’equazione avrà come soluzione uno e un solo numero reale (positivo), in quanto la soluzione di un’equazione di primo grado, se esiste, è unica.

Questo numero reale sarà quindi la misura della quarta grandezza X, e poiché, tra grandezze omogenee, ad ogni numero reale corrisponde una e una sola grandezza, questa quarta proporzionale esiste ed è unica.

Grandezze direttamente proprozionali

Consideriamo due classi di grandezze:

A, B, C, D, ….

A’, B’, C’, D’,….

Queste due classi si dicono in corrispondenza biunivoca quando ad ogni grandezza della prima classe corrisponde una e una sola grandezza della seconda e viceversa.

Le grandezze A e A’, B e B’, C e C’, .. si dicono corrispondenti.

Le grandezze di queste due classi si dicono direttamente proporzionali quando il rapporto di due grandezze qualunque della prima classe è uguale al rapporto delle due grandezze corrispondenti della seconda classe, cioè quando valgono le proporzioni :

A : B = A’ : B’ ; A : C = A’ : C’ ; B : C = B’ : C’ ; …

Se poi le grandezze della prima classe sono omogenee con quelle della seconda, allora possiamo permutare i medi:

A : A’ = B : B’ ; A : A’ = C : C’ ; B : B’ = C : C’ ; …..

E, applicando la proprietà transitiva dell’uguaglianza:

A : A’ = B : B’ = C : C’ = ….=k,

da cui segue che il rapporto tra due grandezze corrispondenti è costante. Questo rapporto costante è un numero detto costante di proporzionalità.

Se le grandezze della prima classe non fossero omogenee con quelle della seconda, dovremmo passare dalla proprozionalità tra le grandezze a quella tra le loro misure (reso sempre possibile dal teorema fondamentale), ed in questo caso sarebbe il rapporto tra le loro misure ad essere costante.

Per determinare se due classi di grandezze sono direttamente proporzionali si applica il seguente teorema (1):

TEOREMA 1. Condizione necessaria e sufficiente affinchè due classi di grandezze in corrispondenza biunivoca siano direttamente proporzionali è che:

1. a grandezze uguali della prima classe corrispondano grandezze uguali della seconda

2. alla somma di due o più grandezze della prima classe corrisponda la somma delle grandezze corrispondenti della seconda classe.

Dimostrazione → (condizione necessaria)

Dimostriamo che la condizione è necessaria, cioè che se le grandezze sono proporzionali, allora devono valere le due proprietà.

Dette A e B due grandezze della prima classe, e A’, B’ le grandezze corrispondenti della seconda classe, per ipotesi avremo A : B = A’ : B’.

Se A=B , il loro rapporto è 1, e tale deve essere il rapporto tra A’ e B’, da cui segue A’ = B’.

Quindi la prima proprietà è verificata.

Applichiamo ora alla proporzione data la proprietà del comporre (A + B) : A = (A’ + B’) : A’

Se C è la grandezza della prima classe tale che C = A + B, sostituendo nella proporzione avremo:

C : A = (A’ + B’) : A’

Se C’ è la grandezza che corrisponde a C, poiché per ipotesi le due classi di grandezze sono direttamente proporzionali, dovrà valere anche la seguente proporzione:

(A + B) : A = C‘ : A’ , e per l’unicità della quarta proporzionale dovrà essere C’ = A’ + B’.

Anche la seconda proprietà risulta dunque verificata.

Dimostrazione ← (condizione sufficiente)

Dimostriamo ora che la condizione è sufficiente: se valgono le due proprietà, le due classi di grandezze sono direttamente proporzionali.

Consideriamo due grandezze qualunque della prima classe A e B; possono essere uguali o disuguali.

Se A = B, allora per la prima proprietà sarà pure A’ = B’; poiché A : B = 1 e A’ : B’ = 1, per la proprietà transitiva dell’uguaglianza dovrà essere A : B = A’ : B’, quindi il rapporto tra due grandezze qualunque della prima classe è uguale al rapporto delle grandezze corrispondenti della seconda, e perciò le due classi di grandezze sono direttamente proporzionali.

Supponiamo ora A e B disuguali, sia ad esempio A > B. Questo vuol dire che esiste una terza grandezza C tale che A = B + C. Per la seconda proprietà, a B + C corrisponde B’ + C’ , e per la prima proprietà, ad A = B + C corrisponde A’ = B’ + C’, da cui si deduce che A’ > B’.

Analogamente si dimostra che se A < B, allora A’ < B’.

Sempre per la seconda proprietà, moltiplicando le grandezze per uno stesso numero naturale avremo che ad nA corrisponderà nA’ e ad mB corrisponderà mB’. Per quanto premesso, avremo che se nA = mB, sarà anche nA’ = mB’; se nA > mB, sarà anche nA’ > mB’ ed infine, se nA < mB , ne deriverà che nA’ < mB’.

Questo vuol dire che, andando a costruire il rapporto tra le grandezze, avremo:

Dunque i rapporti ammettono gli stessi valori approssimati per difetto o per eccesso, e quindi questi rapporti rappresentano lo stesso numero reale, per cui concludendo si ha:

A : B = A’ : B’. In questo modo la tesi è verificata.

Grandezze inversamente proporzionali

Le grandezze di due classi in corrispondenza biunivoca si dicono inversamente proporzionali quando il rapporto di due grandezze qualunque della prima classe è uguale al rapporto inverso delle due grandezze corrispondenti della seconda classe, cioè quando valgono le proporzioni:

A : B = B’ : A’ ; A : C = C’ : A’ ; B : C = C’ : B’ ; …

Se dalla proporzionalità tra le grandezze passiamo a quella tra le loro misure avremo:

a : b = b’ : a’ ; a : c = c’ : a’ ; b : c = c’ : b’ , …

Applicando la proprietà fondamentale della proporzionalità tra numeri (il prodotto dei medi è uguale al prodotto degli estremi) avremo:

aa’ = bb’ ; aa’ = cc’ ; bb’ = cc’ ; ….

E, applicando la proprietà transitiva dell’uguaglianza:

aa’ = bb’ = cc’ = ….=k,

da cui segue che il prodotto tra le misure di due grandezze corrispondenti è costante. Anche in questo caso il prodotto costante è un numero detto costante di proporzionalità.

Teoremi su particolari classi di grandezze direttamente proporzionali

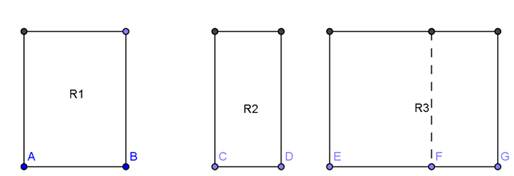
TEOREMA 2. I rettangoli aventi aventi altezze congruenti sono proporzionali alle rispettive basi.

Dimostrazione

Consideriamo la classe di grandezze costituita da tutti i rettangoli con altezze congruenti e la classe costituita dalle rispettive basi. Queste due classi sono in corrispondenza biunivoca, in quanto ad ogni rettangolo corrisponde una ed una sola base e viceversa.

Per dimostrare che queste due classi sono direttamente proporzionali applichiamo il teorema 1 dimostrato precedentemente. Dobbiamo cioè verificare che siano soddisfatte le due proprietà.

Prima proprietà: a grandezze uguali della prima classe devono corrispondere grandezze uguali della seconda.

Si nota facilmente che questa proprietà è sempre verificata, in quanto se si suppone che AB = CD, allora anche i rettangoli che hanno questi segmenti come base, avendo anche le altezze congruenti, saranno sicuramente congruenti.

Seconda proprietà: ad un segmento che sia la somma di due segmenti deve corrispondere un rettangolo che sia la somma di due rettangoli aventi quei segmenti come base.

Supponiamo infatti EG = AB + CD; prendiamo su EG il punto F che divida il segmento in due parti: EF=AB, FG=CD. Tracciando la perpendicolare in F ad EG, questa divide il rettangolo R3 in due rettangoli rispettivamente congruenti ad R1 e ad R2, e quindi R3= R1+R2.

Poiché dunque valgono le due proprietà richieste dal teorema, avremo che:

R1 : R2 = AB : CD, R2 : R3 = CD : EG, … , e quindi le due classi di grandezze sono direttamente proporzionali.

In modo analogo si dimostra che:

I rettangoli aventi basi congruenti sono direttamente proporzionali alle rispettive altezze.

Gli archi di un stessa circonferenza sono direttamente proporzionali ai corrispondenti angoli al centro.

Se tra quattro grandezze omogonee è vera la proporzione x : y = v : z, quali delle seguenti proporzioni sono vere di conseguenza?

[A] x : v = y : z [B] x : z = v : y [C] v : x = x : y [D] z : y = v : x

Sapendo che 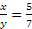completa la proporzione x : z = … : …
Sapendo che 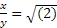completa la proporzione x : z = … : ...
Quattro grandezze A, B, C, D sono tali che 3A=2B, 3C=2D. Domostra verifica se sono in proporzione e in caso affermativo costruisci la proporzione.
Dimostra che se vale la proporzione 3A : 2B = 3C : 2D vale anche la proporzione A : B = C : D

Siano A, B, C, D, E, F, G grandezze omogenee, dimostra che, se A : B = C : D e B : G = F : C dimostra che A : F = G : D.

Le misure delle lunghezze dei lati di un triangolo sono proporzionali ai numeri 5, 6 e 10, sapendo che il perimetro misura 273 cm, determina le misure dei lati del triangolo.
Stabilire se in una stessa circonferenza le corde sono direttamente proporzionali ai corrispondenti angoli (convessi) al centro.
Le ampiezze degli angoli di un triangolo sono proporzionali ai numeri 6, 8, 10, determina le ampiezze degli angoli.
Gli angoli acuti di un triangolo rettangolo sono proporzionali ai numeri 3 e 4, determina le ampiezze degli angoli.
I lati di un rettangolo sono proporzionali ai numeri 6 e 15, sapendo che il perimetro del rettangolo misura 120 cm, determina le misure in cm dei lati del rettangolo.
Determina le misure dei lati di un trapezio sapendo che sono proporzionali ai numeri 3, 4, 5, 4 e che il perimetro è 80cm. Di che tipo di trapezio si tratta?
Il perimetro di un rettangolo misura 12 m. Sapendo che le sue misure sono nel rapporto 2/3, determina le misure dei lati.
Le misure di due segmenti sono tali che la loro differenza è 23 cm e che il loro rapporto è 4/5. Determina attraverso una proporzione le misure dei segmenti.
Determina le ampiezze degli angoli di un triangolo rettangolo sapendo che stanno tra di loro come 7 sta a 4.
La differenza di due segmenti misura 7cm, determina le loro misure sapendo che

(a) uno è il doppio dell'altro

(b) uno è il triplo dell'altro

(d) uno è la quarta parte dell'altro

La somma di due segmenti misura 12cm, determina le loro misure sapendo che

(a) uno è il doppio dell'altro

(b) uno è il triplo dell'altro

(d) uno è la quarta parte dell'altro

Determina le misure di due angoli α e β sapendo che

(a)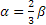

(b)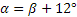

(c)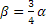

(d) 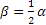e α e β sono complementari

Teorema di Talete, caso generale

TEOREMA DI TALETE. Un fascio di rette parallele determina su due trasversali classi di segmenti direttamente proporzionali.

Assumiamo come ipotesi di avere cinque rette parallele a, b, c, d, e. Dimostriamo che sono in proporzione i segmenti

AB : A'B' = BC : B'C' = AC : A'C' = BD : B'D' = …

A questo scopo ricorriamo alla condizione necessaria e sufficiente dimostrata nel capitolo sulla proporzionalità tra grandezze: condizione necessaria e sufficiente affinchè due classi di grandezze in corrispondenza biunivoca siano direttamente proporzionali è che:

1) a grandezze uguali della prima classe corrispondano grandezze uguali della seconda;

2) alla somma di due o più grandezze della prima classe corrisponda la somma delle grandezze corrispondenti della seconda classe.

La prima proprietà è stata dimostrata nel capitolo 5, quando abbiamo esposto il teorema di Talete: a segmenti congruenti su una trasversale corrispondono segmenti congruenti sull’altra trasversale.

Dimostriamo allora che vale anche la seconda proprietà.

Consideriamo il fascio di rette parallele tagliato da due trasversali della figura.

Abbiamo come ipotesi che CD = AB + BC, dobbiamo dimostrare che C'D' = A'B' + B'C'.

Poiché CD = AB + BC, determiniamo al suo interno il punto E che lo divide nei due segmenti: CE=AB, ED=BC. Tracciamo la parallela alle rette date passante per F, che intersecherà la trasversale t' nel punto F' . Per la prima parte del teorema, avremo che da CF=AB segue che C'F' = A'B' e da FD = BC segue che F'D'=B'C'. Ma C'D'=C'F' + F'D' = A'B' + B'C'.

Conseguenze del teorema di Talete

Dal teorema di Tale discendono due importanti corollari

COROLLARIO 1. Una retta parallela ad un lato di un triangolo determina sugli altri due lati, o sui loro prolungamenti, segmenti proporzionali.

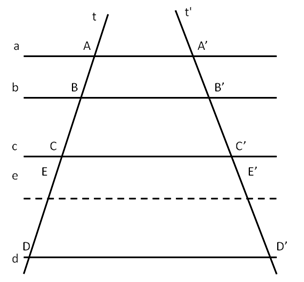
Dimostrazione

Sia ABC il triangolo in questione. Tracciamo una retta parallela al lato BC che intersechi gli altri due nei punti D ed E. Vogliamo dimostrare che AE : AD = EC : DB.

Tracciamo una retta passante per A e parallela a DE e a BC. Ci troviamo così nelle condizioni di poter applicare il teorema di Talete, in quanto abbiamo tre rette parallele tagliate da due trasversali (AB ed AC), per cui possiamo scrivere la proporzione tra segmenti corrispondenti AE : AD = EC : DB.

La stessa dimostrazione vale nel caso in cui la parallela al lato BC intersecasse i prolungamenti dei lati AB e AC.

COROLLARIO 2. La retta che divide due lati di un triangolo (o i loro prolungamenti) in segmenti proporzionali è parallela al terzo lato.

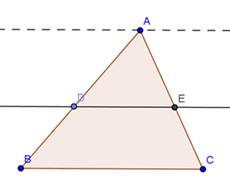
Dimostrazione

Abbiamo in ipotesi che AE : AD = AC : AB e dobbiamo dimostrare che DE è parallela a BC.

Ragioniamo per assurdo; neghiamo quindi la tesi e supponiamo che DE non sia parallela a BC. Esisterà allora un’altra retta passante per D e che sia parallela a BC; questa retta intersecherà il lato AC in un punto F. Per il teorema precedente avremo che AF : AD = AC : AB.

Ma per il teorema della quarta proporzionale sappiamo che la quarta grandezza che con le tre date forma una proporzione deve essere unica, e quindi il punto F deve coincidere con E e la retta DF coincidere con la retta DE, che perciò è parallela a BC.

Un’altra importante conseguenza del teorema di Talete è il teorema della bisettrice.

TEOREMA DELLA BISETTRICE. la bisettrice di un angolo interno di un triangolo divide il lato opposto in parti proporzionali agli altri due lati.

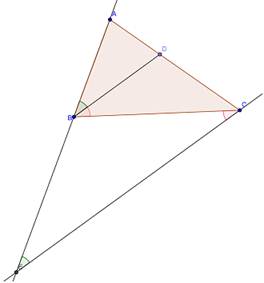Dimostrazione

L’ipotesi è 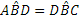; la tesi AD : DC = AB : BC.

Dal vertice C tracciamo la parallela alla bisettrice BD che incontra il prolungamento del lato AB in E. Notiamo le seguenti congruenze tra angoli:

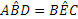in quanto corrispondenti rispetto alle parallele BD ed EC tagliate da AE;

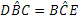in quanto alterni interni rispetto alle parallele BD ed EC tagliate da BC.

Confrontando queste congruenze con quella in ipotesi ed applicando la proprietà transitiva della congruenza possiamo scrivere 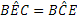. Dunque il triangolo BEC è isoscele e per questo ha due lati congruenti BE = BC.

Applichiamo ora il primo corollario del teorema di Talete al triangolo AEC si ha AB : BE = AD : DC.

Per quanto appena dimostrato possiamo sostituire BC a BE ed avremo AB : BC = AD : DC.

Determina in ogni figura la misura mancante, indicata con un punto interrogativo.
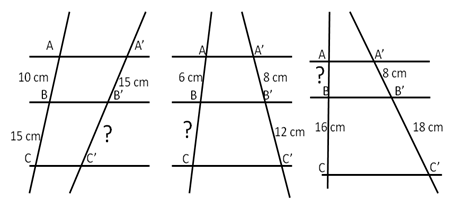
Con riferimento alla figura, quali proporzioni sono conseguenza del teorema di Talete?

[A] u : v = m : n

[B] u : m = v : n

[C] (u+m) : m = (v+n) : n

[D] v : m = u : n

[E] (u + v) : (m + n) = m : n

[F] (m-u) : u = (n-v) : v

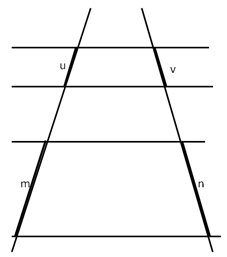
In figura c'è un triangolo e una delle sue bisettrici, quali proporzioni sono conseguenza del teorema della bisettrice?

[A] a : b = x : y

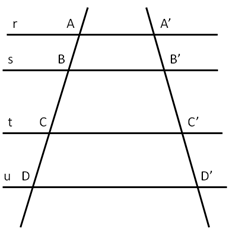
Sapendo che le rette r, s, t, u sono parallele completa le proporzioni

(a) AB : CD = … : ...

(b) AC : BD = … : …

(d) AC : A'C' = … : …

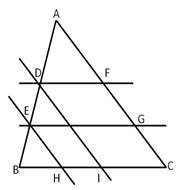Nel triangolo ABC, individua sul lato AB i punti D ed E, con D più vicino ad A. Da D ed E traccia le parallele sia al lato AC che al lato BC, come in figura. Dimostra che sussiste la seguente proporzione AC:BC=FG:HI.
Dato un triangolo qualunque ABC, si consideri il punto medio M del lato AB. Si consideri il segmento parallelo al lato BC che parte da M ed incontra il lato AC nel punto N. Si prolunghi questo segmento di un segmento ND uguale ad MN. Dimostrare che il quadrilatero MDCB è un parallelogramma. Esplicita ipotesi, tesi, fai il disegno e dimostra la tesi.
Dato un parallelogramma ABCD, si consideri M il punto medio del lato AB. Si congiunga il vertice D con il punto M; si congiunga il vertice A con il punto medio N del segmento DM. Dimostrare che la retta AN divide la diagonale DB del parallelogramma in due parti di cui una è il doppio dell’altra.
Due rette incidenti r e s si incontrano in un punto A; sulla retta r considera i punti A' e A”, individua su s le proiezioni ortogonali di A' e A” e chiama questi punti rispettivamente con B' e B”. Dimostra che sussiste la seguente proporzione AA' : AA” = BB' : BB”.
Dal baricentro G di un triangolo ABC manda la parallela al lato AB, sia A' il punto in cui questa parallela incontra il lato AC. Dimostra che CA' è il doppio di A'A. Ricorda le proprietà del baricentro.
Dato il trapezio ABCD, sia E il punto di intersezione dei due lati non paralleli AD e BC. Dimostra che una qualsiasi retta per E che incontri i lati paralleli del trapezio nei punti K e L determina due segmenti EK e KL il cui rappoprto è costante.
Dimostrare che, in un trapezio, il segmento che congiunge i punti medi dei lati non paralleli è uguale alla semisomma delle basi.
Nel parallelogramma ABCD si individuino il punto E su AB tale che AB : AE = 3 : 2 e il punto F su DC tale che DC : FC = 3 : 2. Traccia la diagonale DB e le rette AF ed EC, le quali intersecano DB rispettivamente in L e in M. A quali numeri sono proporzionali i segmenti DL, LM, MB?
Dimostra che in un triangolo ABC la mediana AM è il luogo dei punti medi delle parallele al lato BC.
Nel triangolo ABC prendi un punto qualsiasi D su AB, da D traccia la parallela ad AC che incontra BC in E, da E traccia la parallela ad AB che incontra AC in F, da F traccia la parallela a BC che incontra AB in G, da G la parallela ad AC che incontra BC in H, da H la parallela ad AB che incontra AC in I e così via. Ripeti questa costruzione fino a che non trovi il primo punto che va a sovrapporsi a uno dei punti trovati in precedenza. Esiste questo punto? Qual è? Dimostra perché.
Nel triangolo ABC traccia la bisettrice AK dell'angolo in A. Sapendo che la somma dei lati adiacenti all'angolo misura 47cm, che BK : CK = 3 : 4 e che BK misura 7cm, determinare le misure dei lati del triangolo.
Dal punto K della mediana AM del triangolo ABC traccia le parallele ai tre lati del triangolo, siano D ed E i punti di intersezione di AB e AC con la parallela a BC, siano F e G i punti di intersezione delle altre due parallele con il lato BC. Dimostra che AK è mediana del triangolo ADE e che KM è la mediana del triangolo KFG.
Sia E il punto di intersezione delle diagonali del trapezio ABCD, dimostra che AE : EC = BE : ED.
Sia AM la mediana del triangolo ABC. Dai vertici B e C traccia le parallele alla mediana AM. Sulla parallela per B individua un punto K e sulla parallela per C il punto L tali che AK è congruente a AL. Dimostra che KAL sono allineati.
Dimostra che in qualsiasi triangolo ABC la retta che passa per i punti medi dei lati AB e AC divide in due parti uguali l'altezza relativa a BC.

Questo libro, eccetto dove diversamente specificato, è rilasciato nei termini della licenza Creative Commons Attribuzione – Condividi allo stesso modo 3.0 Italia (CC BY-SA 3.0) il cui testo integrale è disponibile al sito

http://creativecommons.org/licenses/by-sa/3.0/it/legalcode

Tu sei libero:

di riprodurre, distribuire, comunicare al pubblico, esporre in pubblico, rappresentare, eseguire e recitare quest'opera, di modificare quest'opera, alle seguenti condizioni:

Attribuzione — Devi attribuire la paternità dell'opera nei modi indicati dall'autore o da chi ti ha dato l'opera in licenza e in modo tale da non suggerire che essi avallino te o il modo in cui tu usi l'opera.

Condividi allo stesso modo — Se alteri o trasformi quest'opera, o se la usi per crearne un'altra, puoi distribuire l'opera risultante solo con una licenza identica o equivalente a questa.

Autori

Gemma Fiorito: teoria

Angela D’Amato: teoria

Cristina Mocchetti: integrazioni

Antonio Bernardo: integrazioni, esercizi

Lucia Rapella: correzioni

Riccardo Sala: correzioni

Germano Pettarin: esercizi

Francesco Camia: correzioni

Collaborazione, commenti e suggerimenti

Se vuoi contribuire anche tu alla stesura e aggiornamento del manuale Matematica C3 o se vuoi inviare dei commenti e/o suggerimenti scrivi a antoniobernardo@matematicamente.it

Versione del documento

Versione 1.2 del 22.11.2011

Fonte: http://www.matematicamente.it/staticfiles/matematica-C3/GRC7-misura-proporzionalita-v1.2.odt

Autori del testo: indicati nel testo

Parola chiave google : Geometria razionale misura proporzionalità tipo file : doc

Geometria razionale misura proporzionalità