• 
• 

 

Principali teoremi della geometria

 

 

---

 

Principali teoremi della geometria

 

I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

  

N.B. Per affermare che un triangolo è isoscele o rettangolo oppure che un quadrilatero è un parallelogramma o un rettangolo o un rombo o un quadrato o un trapezio o un trapezio isoscele, c’è sempre la possibilità di sfruttare la definizione!!!

 

 

Congruenza, angoli e segmenti

 

• Proprietà transitiva della congruenza: due figure congruenti ad una terza sono congruenti tra loro.
• Somme o differenze di segmenti congruenti sono congruenti.
• Doppi, tripli, metà … di uno stesso segmento o di segmenti congruenti sono congruenti.
• Somme o differenze di angoli congruenti sono congruenti.
• Doppi, tripli, metà … di uno stesso angolo o angoli congruenti sono congruenti.
• Angoli complementari o supplementari di uno stesso angolo o di angoli congruenti sono congruenti.
• Angoli opposti al vertice sono congruenti.
• Due angoli congruenti e supplementari sono retti.

Triangoli

 

• I criterio: se due triangoli hanno ordinatamente congruenti due lati e l’angolo tra essi compreso allora sono congruenti.
• II criterio: se due triangoli hanno ordinatamente congruenti due angoli e il lato tra essi compreso allora sono congruenti.
• III criterio: se due triangoli hanno ordinatamente congruenti tre lati allora sono congruenti.
• Un triangolo è isoscele se e solo se ha gli angoli alla base congruenti.
• Un triangolo è isoscele  se e solo se l’altezza e la mediana relativa alla base e la bisettrice dell’angolo al vertice coincidono.
• Se un triangolo è isoscele allora le altezze e le mediane relative ai lati congruenti e le bisettrici relative agli angoli congruenti sono congruenti e si tagliano in parti congruenti.
• Se due triangoli sono congruenti allora le altezze e le mediane relative ai lati congruenti e le bisettrici relative agli angoli congruenti sono congruenti.

 

 

Rette parallele e perpendicolari

 

• Due rette sono parallele se e solo se, tagliate da una trasversale, formano:
• angoli alterni (interni o esterni) congruenti,
• angoli corrispondenti congruenti,
• angoli coniugati (interni o esterni) supplementari.
• Due perpendicolari ad una stessa retta sono parallele tra loro.
• Se due rette sono parallele ogni perpendicolare ad una è perpendicolare all’altra.
• Proprietà transitiva del parallelismo: due rette parallele a una terza sono parallele tra loro.
• Due angoli aventi i lati paralleli concordi o paralleli discordi sono congruenti; due angoli aventi una coppia di lati paralleli concordi e una coppia di lati paralleli discordi sono supplementari.
• Segmenti paralleli compresi tra rette parallele sono congruenti.

Teorema dell’angolo esterno e criteri particolari (2° generalizzato e triangoli rettangoli)

• Teorema dell’angolo esterno: in un triangolo l’angolo esterno è uguale alla somma degli angoli interni non adiacenti ad esso.
• La somma degli angoli interni di un triangolo è uguale ad un angolo piatto.
• Gli angoli acuti di un triangolo rettangolo sono complementari.
• Gli angoli di un triangoli equilatero sono congruenti ad un terzo di angolo piatto
• Se due triangoli hanno due angoli rispettivamente congruenti hanno congruenti anche i terzi angoli.
• Due triangoli isosceli hanno gli angoli al vertice congruenti se e solo se hanno gli angoli alla base congruenti.
• II criterio generalizzato: se due triangolo hanno rispettivamente congruenti un lato e due angoli allora sono congruenti.
• Criteri dei triangoli rettangoli: due triangoli rettangoli sono congruenti se hanno rispettivamente congruenti:
• un cateto e un angolo acuto,
• l’ipotenusa e un angolo acuto,
• i due cateti,
• un cateto e l’ipotenusa
• Un triangolo rettangolo ha un angolo acuto doppio dell’altro se e solo se l’ipotenusa è il doppio del cateto minore (cioè è la metà di un triangolo equilatero).

 

 

 

Parallelogrammi

• Se un quadrilatero è un parallelogramma allora:
• la diagonale lo divide in due triangoli congruenti,
• i lati opposti sono congruenti ,
• gli angoli opposti sono congruenti,
• gli angoli adiacenti ad uno stesso lato sono supplementari,
• le diagonali hanno lo stesso punto medio.
• Se in un quadrilatero:
• i lati opposti sono congruenti a due a due,
• gli angoli opposti sono congruenti a due a due,
• ha una coppia di lati opposti paralleli e congruenti,
• le diagonali hanno lo stesso punto medio

allora è un parallelogramma.

• In un rettangolo le diagonali sono congruenti.
• Se un parallelogramma ha le diagonali congruenti allora è un rettangolo.
• In un rombo le diagonali sono perpendicolari e bisettrici degli angoli.
• Se un parallelogramma ha le diagonali perpendicolari o bisettrici degli angoli allora è un rombo.
• In un quadrato le diagonali sono congruenti, perpendicolari e bisettrici degli angoli.
•  Se un parallelogramma soddisfa una caratteristica dei rettangoli (definizione o proprietà) e una caratteristica dei rombi (definizione o proprietà) allora è un quadrato. (schema 1: in fondo all’elenco)
• Un triangolo è rettangolo se e solo se la mediana relativa a un lato (ipotenusa) è metà del lato (ipotenusa) stesso (cioè lo divide in due triangoli isosceli).

Trapezi

• Un trapezio è isoscele se e solo se gli angoli adiacenti a ciascuna base sono congruenti.
• In un trapezio isoscele le diagonali sono congruenti e lo dividono in quattro triangoli di cui due congruenti e due isosceli.
• In un trapezio isoscele gli angoli adiacenti ai lati obliqui e gli angoli opposti sono supplementari.
• In un trapezio isoscele le proiezioni dei lati obliqui sulla base maggiore sono congruenti.

 

 

 

Talete con le congruenze

 

• Teorema di Talete: se un fascio di rette parallele è segato da due trasversali allora a segmenti congruenti su una trasversale corrispondono segmenti congruenti sull’altra trasversale.
• Se per il punto medio di un lato di un triangolo si conduce la parallela ad un altro lato, questa dimezza il lato rimanente.
• In un triangolo qualunque il segmento che congiunge i punti medi di due lati è parallelo al terzo lato e congruente alla sua metà.
• La congiungente i punti medi dei lati obliqui di un trapezio è parallela alle basi e congruente alla loro semisomma.
• I punti medi dei lati di un quadrilatero sono vertici di un parallelogramma. (schema 2: in fondo all’elenco)

Luoghi geometrici

                                                                   .

• La bisettrice di un angolo convesso è il luogo dei punti equidistanti dai lati dell’angolo.
• L’asse di un segmento è il luogo dei punti equidistanti dagli estremi del segmento.

 

Circonferenze

                            .

• Due circonferenze o due cerchi sono congruenti se e solo se hanno i raggi congruenti.
• In una circonferenza o in circonferenze congruenti:
• ad archi congruenti corrispondono corde e angoli al centro congruenti,
• a corde congruenti corrispondono archi e angoli al centro congruenti,
• ad angoli al centro congruenti corrispondono archi e corde congruenti.
• In una circonferenza la bisettrice di un angolo al centro dimezza l’arco e la corda corrispondenti (e viceversa).
• Teorema della retta diametrale: in una circonferenza :
• la retta passante per il centro e perpendicolare ad una corda passa per il punto medio della corda e dimezza pure l’arco e l’angolo al centro corrispondenti,
• la retta passante per il centro e per il punto medio di una corda è perpendicolare alla corda stessa e dimezza l’arco e l’angolo al centro corrispondenti,
• l’asse di una corda passa per il centro.
• In una circonferenza o in circonferenze congruenti: due corde sono congruenti se e solo se congruenti hanno distanze congruenti dal centro,
• Una retta è tangente ad una circonferenza se e solo se è perpendicolare al raggio nel punto di contatto.
• Ogni angolo alla circonferenza è metà del corrispondente angolo al centro.
• In una circonferenza o in circonferenze congruenti :
• ad archi congruenti corrispondono angoli alla circonferenza congruenti,
• ad angoli alla circonferenza congruenti corrispondono archi congruenti.
• Ogni triangolo inscritto in una semicirconferenza  è rettangolo.
• Teorema delle tangenti: se da un punto esterno ad una circonferenza si conducono le due tangenti:
• i segmenti di tangente compresi fra tale punto e i punti di contatto sono congruenti.
• la congiungente il punto esterno con il centro della circonferenza è bisettrice sia dell’angolo formato dalle due tangenti, sia dell’angolo formato dai raggi che vanno ai punti di tangenza,
• la congiungente il punto esterno con il centro della circonferenza è asse della corda che unisce i due punti di tangenza.                                                                                                          
• Teorema del baricentro: il baricentro divide ciascuna mediana in due parti di cui quella contenente il vertice è doppia dell’altra.
• Un quadrilatero è inscrittibile in una circonferenza se e solo se ha gli angoli opposti  supplementari.
• Un quadrilatero è circoscrivibile in una circonferenza se e solo se la somma di due lati opposti è congruente alla somma degli altri due  

 

Equivalenza

                                                                                           .     

• Proprietà transitiva dell’equivalenza: due superficie equivalenti ad una terza sono equivalenti tra loro.
• Somme o differenze di superficie equivalenti sono equivalenti.
• Figure equicomposte (somme di figure congruenti) sono equivalenti.
• Due parallelogrammi sono equivalenti se hanno basi e altezze corrispondenti congruenti.
• Un rettangolo è equivalente ad un parallelogramma avente la stessa base e la stessa altezza.
• Un triangolo è equivalente ad un parallelogramma avente la stessa altezza e metà base.
• Un trapezio è equivalente ad un triangolo avente la stessa altezza e per base la somma delle basi del trapezio.
• Un poligono circoscritto è equivalente ad un triangolo avente per base il perimetro del poligono e per altezza il raggio della circonferenza inscritta.
• I teorema di Euclide: in ogni triangolo rettangolo il quadrato di un cateto è equivalente al rettangolo dell’ipotenusa e della proiezione del cateto stesso sull’ipotenusa.
• II teorema di Euclide: in ogni triangolo rettangolo il quadrato dell’altezza relativa all’ipotenusa è equivalente al rettangolo delle proiezioni dei due cateti sull’ipotenusa.
• Teorema di Pitagora: un triangolo è rettangolo se e solo se il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati dei due cateti    

Talete
.

• Teorema di Talete: un fascio di rette parallele determina su due trasversali due classi di segmenti direttamente proporzionali.
• La parallela ad un lato di un triangolo divide gli altri due lati in parti proporzionali.
• Se una retta divide in parti proporzionali due lati di un triangolo allora è parallela al terzo lato.
• Teorema della bisettrice: la bisettrice di un angolo interno di un triangolo di vide il lato opposto in parti proporzionali agli due lati.

Similitudine

 

• I criterio di similitudine: due triangoli sono simili se hanno due angoli ordinatamente congruenti.
• II criterio di similitudine: due triangoli sono simili se hanno un angolo congruente compreso tra lati proporzionali.
• III criterio di similitudine: due triangoli sono simili se hanno i tre lati ordinatamente proporzionali.
• Una retta parallela ad un lato di un triangolo stacca da esse un triangolo simile al dato.
• Tutti i triangoli equilateri sono simili tra loro.
• Due triangoli isosceli sono simili se hanno congruenti  gli angoli alla base o gli angoli al vertice.
• Due triangoli rettangoli sono simili se hanno un angolo acuto congruente o i cateti proporzionali.
• In due triangoli simili le altezze, le mediane, le bisettrici, i raggi delle circonferenze inscritte e circoscritte, i perimetri stanno tra loro come due lati omologhi; le superfici stanno tra loro come i quadrati di due lati omologhi.
• I Euclide: in un triangolo rettangolo il cateto è medio proporzionale tra l’ipotenusa e la proiezione del cateto stesso sull’ipotenusa.
• II Euclide: in un triangolo rettangolo l’altezza relativa all’ipotenusa è media proporzionale tra le proiezioni dei due cateti sull’ipotenusa.
• Teorema delle due corde: se due corde di una circonferenza si intersecano. I segmenti di una sono inversamente proporzionali ai segmenti dell’altra.
• Teorema delle due secanti: se da un punto esterno ad una circonferenza si conducono due secanti, le intere secanti sono inversamente proporzionali alle loro parti esterne.
• Teorema della tangente e della secante: se da un punto esterno ad una circonferenza si conducono una tangente ed una secante, il segmento di tangente è medio proporzionale tra l’intera secante e la sua parte esterna.

Formule particolari

• diagonale di un quadrato in funzione del lato :                      d = l ;
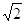• altezza di un triangolo equilatero in funzione del lato:          h = ;
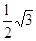• in un triangolo rettangolo avente gli angoli acuti di 30° e 60°:
• l’ipotenusa è il doppio del cateto minore;
• il cateto maggiore è il cateto minore per  ;
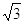• il cateto maggiore è ½ ipotenusa per ;
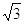• area di un triangolo in funzione dei lati (formula di Erone): 

-    S  =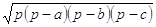

• lati di poligoni regolari in funzione del raggio della circonferenza circoscritta:

-     l3  =  r  ;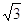             

•  l4  =  r  ;    

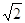-     l6  =  r .

• raggio delle circonferenze inscritte e circoscritte in funzione dei lati di un triangolo:

-     r   = S / p ;             

•  R  = a b c / 4 S .

 

 

Fonte: http://www.liceocavalieri.it/public/classi/archiviorisorse%5CV1PRINCIPALI_TEOREMI_DELLA_GEOMETRIA.doc

 

Autore del testo: non indicato nel documento di origine

 

 

 

Principali teoremi della geometria

 

 

Principali teoremi della geometria

 

Disclaimer

Questo sito non rappresenta una testata giornalistica e viene aggiornato senza alcuna periodicità, esclusivamente sulla base della disponibilità del materiale, pertanto non è un prodotto editoriale sottoposto alla disciplina di cui all'art. 1, comma III della Legge n. 62 del 7.03.2001. I riassunti , gli appunti i testi e le citazioni contenuti nel nostro sito sono messi a disposizione gratuitamente a studenti, ricercatori, professori, tecnici con scopi illustrativi didattici e scientifici con il concetto del fair use e con obiettivo del rispetto della direttiva europea 2001/29/CE e della legge n. 633 art. 70 e dlg 68. Il sito è curato e coordinato dall’autore al solo scopo informativo e didattico. Pur ritenendo le fonti utilizzate affidabili, l'autore di questo sito non garantisce l'accuratezza e l'integrità delle informazioni contenute e pertanto declina ogni responsabilità per eventuali problemi o danni causati da errori o omissioni, nel caso tali errori o omissioni risultino da negligenza, caso fortuito o altra causa. Tutti gli appunti, le citazioni i testi e le immagini , sono proprietà dei rispettivi autori o case di produzione che ne detengono i diritti, qualora gli aventi diritto si ritenessero danneggiati dall'inserimento in questo sito dei predetti files o fossero stati inavvertitamente inseriti immagini, informazioni, testi od altro materiale coperto da Copyright saranno immediatamente rimossi e/o ne saranno citate le fonti su semplice segnalazione all' indirizzo e-mail indicato nella pagina contatti .

Gli obiettivi di questo sito sono il progresso delle scienze e delle arti utili in quanto pensiamo che siano molto importanti per il nostro paese i benefici sociali e culturali della libera diffusione di informazioni utili. Tutte le informazioni e le immagini contenute in questo sito vengono qui utilizzate esclusivamente a scopi didattici, conoscitivi e divulgativi. Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione). In questo sito abbiamo fatto ogni sforzo per garantire l'accuratezza dei tools, calcolatori e delle informazioni, non possiamo dare una garanzia o essere ritenuti responsabili per eventuali errori che sono stati fatti, i testi utilizzati sono stati prelevati da siti che li hanno messi a disposizione gratuitamente per farli conoscere nel web con scopi didattici. Se trovate un errore su questo sito o se trovate un testo o tool che possa violare le leggi vigenti in materia di diritti di autore, comunicatecelo via e-mail e noi provvederemo tempestivamente a rimuoverlo.

 

---

 

---

 

Designed by Larapedia.com 1998 -2011