Curve algebriche

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Curve algebriche

GEOMETRIA ANALITICA

Curve, Rette, Coniche, Cubiche, Curve trascendenti, Superficie in R³

Curve in R²

01 – Definizioni.

Consideriamo il piano euclideo R² dotato di un sistema di assi cartesiani ortogonali Oxy .
Esso sarà chiamato d’ora in poi più semplicemente piano cartesiano. L’equazione :



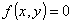
dove   f   è una funzione reale continua definita su un opportuno dominio di   x e y ,
rappresenta l’equazione di una curva piana i punti della quale soddisfano l’equazione
data.

Esempio :

        x ² + y ² - 1 = 0   è l’equazione di una circonferenza di centro O e raggio 1



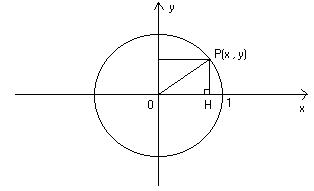
        in quanto ogni punto   P   della circonferenza è tale per cui applicando il teorema
        di Pitagora al triangolo   OHP   si ottiene PH ² + HO ² = 1 e quindi, sostituendo
        PH = y   e   HO = x , si ha verificata l’equazione.

Risolvendo (ove possibile) l’equazione di una curva rispetto ad una variabile, per esempio
la   y , si ottiene :



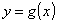
Questa è l’equazione della medesima curva in forma esplicita.

L’equazione in forma esplicita della circonferenza dell’esempio precedente risulta essere
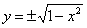(si noti che questa equazione non è una funzione perché per un valore
di   x , la   y assume due valori).

Se la funzione 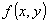è un polinomio in x ed y , la curva si dice algebrica ed il grado
del polinomio si dice ordine della curva, in caso contrario la curva si dice trascendente.

Le curve algebriche del primo ordine sono le curve di equazione :

        .

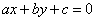Esse sono le rette del piano.

Le curve algebriche del secondo ordine sono le curve di equazione :
        .

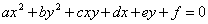Esse sono dette coniche.

Le curve algebriche del terzo ordine sono dette cubiche.

Se l’equazione di una curva è esprimibile come prodotto di due o più funzioni   α ,
β , … , cioè è del tipo 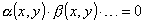  , allora la curva è composta dalle
curve   α = 0 , β = 0 … perché un prodotto è nullo quando è nullo uno dei suoi
fattori. In questo caso la curva si dice riducibile, altrimenti si dice irriducibile.

02 – Intersezioni fra due curve.

Date le curve di equazione 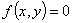   esse possono avere punti in
comune oppure no. I punti in comune fra le due curve si chiamano punti intersezione.

Se le due curve sono algebriche e non hanno parti in comune, vale l’importante teorema
di Bézout (omettiamo la dimostrazione) :

        se   m ed n sono gli ordini delle due curve, il numero di punti di intersezione sono
        m · n . Questi punti possono essere reali o complessi, distinti o coincidenti.

Per determinare le intersezioni fra due curve basta risolvere il sistema fra le due equazioni
che le rappresentano.

Esempi :

            - 1 -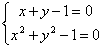

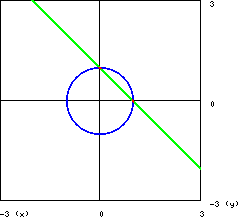
                        si tratta dell’intersezione di una retta con una circonferenza in cui i due
                        punti di intersezione sono distinti e reali. Diamo una soluzione grafica :



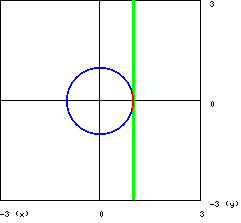
            - 2 -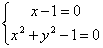

                        si tratta dell’intersezione di una retta con una circonferenza in cui i
                        due punti di intersezione sono coincidenti e reali. Si tratta di un punto
                        di tangenza che può essere interpretato come il passaggio al limite fra
                        retta secante, con due punti di intersezione, e retta tangente, con un solo
                        punto di intersezione. Diamo una soluzione grafica (non appare un singolo
                        punto a causa dello spessore con cui sono state disegnate le curve) :



            - 3 -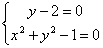

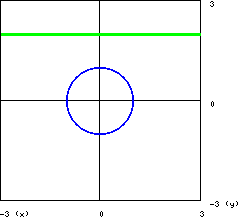
                        si tratta dell’intersezione di una retta con una circonferenza in cui i due
                        punti di intersezione sono distinti e complessi. In questo caso le due curve
                        non hanno punti del piano in comune, i punti di intersezione hanno coordinate
                        complesse. Diamo una soluzione grafica :



03 –Equazione parametrica.

L’equazione di una curva può essere posta nella forma :



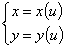
dove   u   è un parametro reale compreso fra due valori prefissati ( a ≤ u ≤ b , dove a
può essere anche -∞ e b può essere anche +∞ ) ed   x(u) , y(u) sono due funzioni
reali continue. Una curva così definita si dice espressa in forma parametrica.

Per passare dalla forma parametrica alla forma esplicita, è sufficiente ricavare il parametro
(ove possibile) da una delle due equazione e sostituirlo nell’altra.

Viceversa, per passare dalla forma esplicita y = g(x) alla forma parametrica è sufficiente
porre   x = u ed   y = g(u) con   u   definito su gli stessi valori in cui è definita la x . Si
noti che le forme parametriche di una curva sono infinite, in quanto il parametro può
essere scelto arbitrariamente.

Esempi :

        -1 - 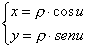           , con 0 ≤ u ≤ 2π , rappresenta una circonferenza di
                        centro O e raggio   ρ .

                        Infatti, elevando al quadrato ambo i membri e sommando membro a
                        membro, si ottiene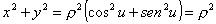

        - 2 -         y = x ² + 2x – 1   è una conica (parabola) in forma esplicita. Una sua
                        forma parametrica è   .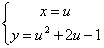

Le curve del tipo 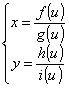  , dove f(u) , g(u) , h(u) ed i(u) sono polinomi del
parametro u , sono dette curve razionali. Le curve razionali sono curve algebriche
mentre non vale il viceversa.

04 – Coordinate polari.

La scelta delle coordinate cartesiane ortogonali non è l’unica possibile. Sul piano è
possibile scegliere infiniti sistemi di riferimento di cui quello cartesiano ortogonale è
sicuramente il più semplice da utilizzare in un grande numero di applicazioni concrete.

Un sistema di coordinate non cartesiane molto importante è il sistema delle coordinate
polari. Esso è definito rispetto ad un usuale sistema di riferimento cartesiano utilizzando
le ben note proprietà trigonometriche dei triangoli rettangoli :



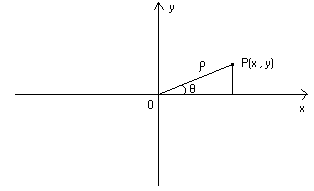
Se il punto   P ha coordinate cartesiane   (x , y) , ρ è l’ipotenusa e θ è l’angolo
con vertice in   O considerato misurato in senso antiorario rispetto al semiasse
positivo   Ox , allora valgono le relazioni :



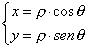
La coppia   (ρ , θ) rappresenta le coordinate polari del punto   P . La coordinata
ρ , che può variare da   0 all’infinito, si chiama raggio vettore mentre la coordinata
θ , che può variare da   0 a   2π , si chiama anomalia. Il punto   O   si chiama polo
e la semiretta   Ox   si chiama asse polare.

La relazione che esprime le coordinate polari in funzione di quelle cartesiane è :



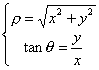
la prima si ricavano elevando al quadrato ambo i membri della precedente e sommando,
la seconda, dividendo ambo i membri.

Si noti che, mentre   ρ è ricavabile direttamente, θ è ricavabile tramite la sua tangente.
Se si desidera utilizzare la funzione arcotangente, occorre notare che il codominio della
suddetta è definito fra - π/2   e   + π/2 .

Esempi :

        - 1 -         la retta   ax + by + c = 0 diventa in coordinate polari aρcosθ + bρsenθ + c = 0 .
                        Si noti che l’equazione della retta espressa in forma polare è più complicata
                        di quella in forma cartesiana.

        - 2 -         la circonferenza   x² + y² - 1 = 0 (di centro O e raggio 1 ) è in forma polare
                        ρ = 1 . In questo caso la forma polare è molto più semplice della forma
                        cartesiana.

Rette in R²

01 – Generalità.

La curva algebrica di primo grado



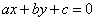
con i parametri   a e b non contemporaneamente nulli, rappresenta una generica retta
del piano cartesiano.

Distinguiamo i vari casi :

        -                      caso con a ≠ 0 , b ≠ 0 :



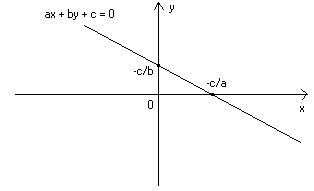
        -                      caso con a = 0 , b ≠ 0 :



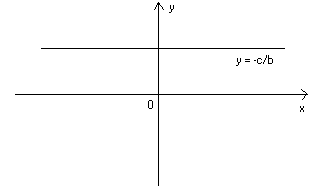
        -                      caso con a ≠ 0 , b = 0 :



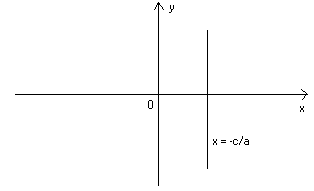
Nel caso in cui   b ≠ 0 , l’equazione della retta può essere messa in forma esplicita :



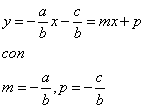
Il parametro   m   si chiama coefficiente angolare della retta ed il parametro p si
chiama ordinata all’origine. Il significato geometrico della forma esplicita di una
retta è il seguente :



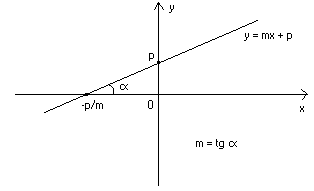
Il coefficiente angolare   m della retta ne rappresenta la pendenza. Considerando il
triangolo rettangolo intercettato dalla retta sugli assi cartesiani, infatti, esso è uguale
alla tangente dell’angolo α (preso a partire dalla semiretta Ox in senso antiorario)
ovvero alla derivata prima della funzione.

Ovviamente la forma esplicita non rappresenta le rette del tipo   x = k , ovvero le
rette parallele all’asse delle y .

02 – Rette per un punto.



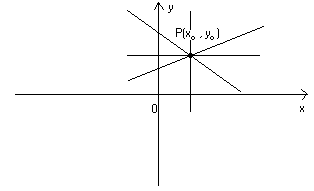
Le infinite rette che passano per il punto 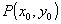  hanno la seguente equazione
(omettiamo la dimostrazione) :



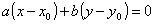
dove a e b sono parametri reali.

03 – Retta per due punti.



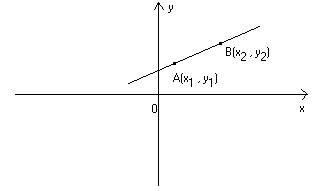
La retta che passa per i punti 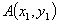   ha la seguente equazione
(omettiamo la dimostrazione) :



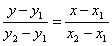
I casi in cui la retta è parallela ad un asse coordinato non sono ovviamente contemplati
in questa equazione in quanto i denominatori si annullerebbero.

04 – Rette parallele.



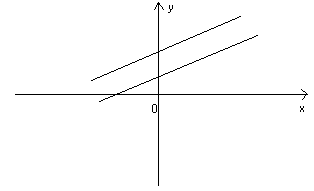
Le rette di equazione 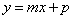  sono parallele quando vale la
relazione :



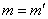
in quanto le due rette hanno la stessa pendenza. Le rette parallele all’asse Oy , non
rappresentabili in forma esplicita, sono ovviamente parallele.

05 – Rette perpendicolari.



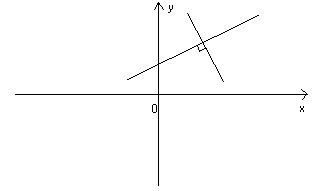
Le rette di equazione 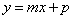  sono perpendicolari quando
vale la relazione :



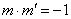
(omettiamo la dimostrazione). Le rette parallele agli assi coordinati vanno ovviamente
considerati a parte. Esse sono le rette   x = k ed y = k’ che sono naturalmente
perpendicolari.

06 – Distanza di un punto da una retta.



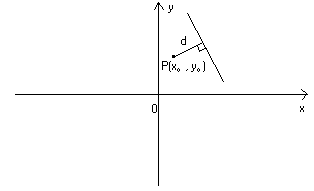
La distanza del punto 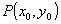  è :



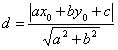
(omettiamo la dimostrazione).

07 – Equazione parametrica della retta.

Una forma parametrica generale della retta è :



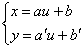
Dove a , a’ , b e b’ sono numeri reali ed il parametro u varia da -∞ a +∞ .

Coniche notevoli

Elenchiamo qui alcune coniche notevoli.

01 – Circonferenza.

Nel piano cartesiano, l’insieme dei punti equidistanti da un punto detto centro, si chiama
circonferenza. Sia C(a , b) il centro ed   R il raggio della circonferenza :



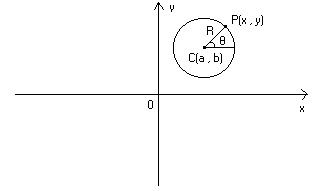
L’ equazione della circonferenza si ottiene ponendo PC ² = R ² ovvero, per il teorema
di Pitagora,   (x – a) ² + (y – b) ² = R ²   da cui, semplificando, si ha x ² + y ² - 2ax - 2by +
+ a ² + b ² - R ² = 0 . Questa equazione si può semplificare ulteriormente ponendo
α = -2a , β = -2b , γ = a ² + b ² - R ² per cui, in definitiva, l’equazione della
circonferenza è :



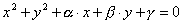
Centro e raggio, espressi in funzione di   α , β , γ , risultano allora :

        .

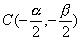La circonferenza è una curva algebrica di secondo ordine cioè è una conica.

Considerando l’angolo θ fra il raggio ed il semiasse positivo   Ox (misurato in senso
antiorario), una equazione parametrica della circonferenza è la seguente :



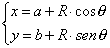
con θ   fra 0 e 2π .

02 – Ellisse.

Nel piano cartesiano, l’insieme dei punti per cui la somma delle distanze da due punti
detti fuochi è costante si chiama ellisse. Siano F(-c , 0) ed F’(c . 0) i due fuochi e
2a   la somma costante (dove a e c sono positivi) :



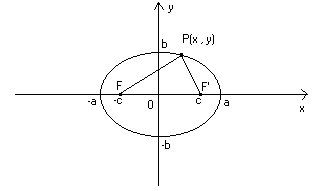
L’equazione dell’ellisse si ottiene ponendo   PF + PF’ = 2a   da cui, applicando due
volte il teorema di Pitagora, si ottiene   .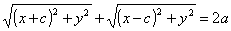
Razionalizzando e semplificando si ottiene   .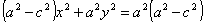
Essendo PF + PF’ > FF’ (per la disuguaglianza triangolare) si ha   2a > 2c cioè
a > c per cui a ² - c ² > 0 . Ponendo b ² = a ² - c ² l’equazione dell’ellisse si
semplifica ulteriormente e diviene :



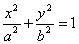
Il significato geometrico dei parametri a , b e c è indicato nel grafico. I quattro punti
di intersezione dell’ellisse con gli assi coordinati si chiamano vertici, i segmenti intercettati
si chiamano assi, e la lunghezza del segmento FF’ si chiama distanza focale.

L’ellisse è una curva algebrica di secondo ordine cioè è una conica.

Una equazione parametrica dell’ellisse è :



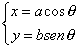
con θ   fra 0 e 2π .

03 – Iperbole.

Nel piano cartesiano, l’insieme dei punti per cui la differenza delle distanze da due punti
detti fuochi è costante si chiama iperbole. Siano F(-c , 0) ed F’(c . 0) i due fuochi e
2a   la differenza costante (dove a e c sono positivi) :



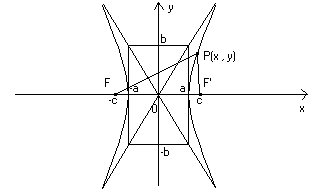
Con procedimento analogo all’ellisse e ponendo b ² = c ² - a ² si ottiene l’equazione :



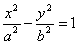
Il significato geometrico dei parametri a , b e c è indicato nel grafico. I due punti di
intersezione dell’iperbole con l’asse Ox si chiamano vertici, la retta FF’ si chiama
asse traverso mentre la retta ad essa normale passante per il punto medio di FF’
si chiama asse non traverso. La lunghezza del segmento FF’ si chiama distanza
focale.

Le rette di equazione 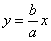  intercettate dal rettangolo indicato in
figura sono gli asintoti dell’iperbole. L’iperbole, per x tendente a +∞ od a -∞ ,
si avvicina a queste rette sempre più (omettiamo la dimostrazione).

Nel caso in cui gli asintoti sono ortogonali, facendo una trasformazione di coordinate
in modo che le nuove coordinate corrispondano agli asintoti, l’iperbole, così detta
equilatera, diventa :



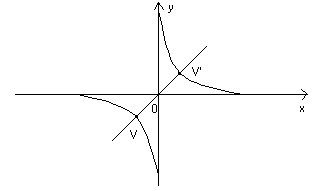
L’equazione dell’iperbole equilatera risulterà (omettiamo la dimostrazione) :



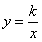
Dove k è un parametro positivo (nel caso di k < 0, l’iperbole è ribaltata rispetto all’asse
Ox , per cui ci riferiamo al solo caso k > 0). Gli asintoti dell’iperbole coincidono, come già
detto, con gli assi cartesiani e le coordinate dei vertici sono .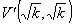

L’iperbole (in entrambe le forme considerate) è una curva algebrica di secondo ordine cioè
è una conica.

Una equazione parametrica dell’iperbole (nella prima forma) è :



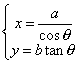
con θ   fra 0 e 2π .

04 – Parabola.

Nel piano cartesiano, l’insieme dei punti per cui la distanza da un punto detto fuoco ed
una retta detta direttrice è costante si chiama parabola. Prendendo la direttrice d
parallela all’asse Ox ed il fuoco F come indicato in figura :



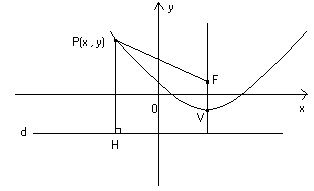
e ponendo PH = PF si ottiene l’equazione (omettiamo la dimostrazione) :



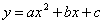
dove   a , b , c sono parametri reali ed a è diverso da 0 .

Il punto V si chiama vertice della parabola e la retta VF si chiama asse. Vertice,
fuoco e direttrice sono dati in funzione dei parametri a , b e c dalle seguenti formule :



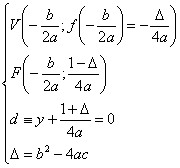
La parabola è una curva algebrica di secondo ordine cioè è una conica.

Cubiche notevoli

Elenchiamo qui alcune cubiche notevoli.

01 – Cubica semplice.

Nel piano cartesiano, la curva di equazione :



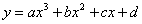
dove a , b , c e d sono parametri reali (a ≠ 0) verrà da noi chiamata cubica semplice.
Rappresentiamo qui il grafico del semplice caso y = x ³ :



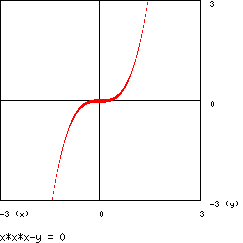
02 – Parabole divergenti di Newton.

Particolarmente importanti sono le seguenti cubiche dette parabole divergenti di Newton.

            - 1 -     parabola con ovale :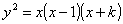

                        dove k è un parametro reale diverso da 0 e da -1 . Nel caso in cui
                        k = 1 il grafico è :



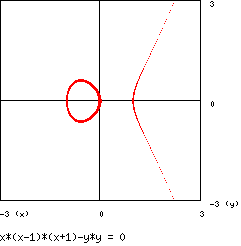
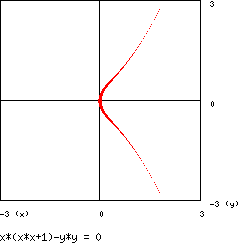
        - 2 -         parabola pura :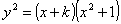

                        dove k è un parametro reale. Nel caso in cui k = 0 il grafico è :



            - 3 -     parabola puntata :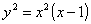

                        il grafico è :



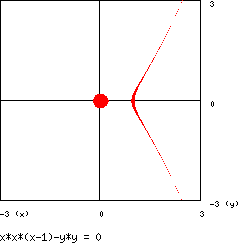
                        Il punto (0 , 0) è un punto isolato della cubica (esso appare ingrandito
                        per via dell’approssimazione numerica utilizzata).

        - 4 -         parabola nodata :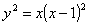

                        il grafico è :



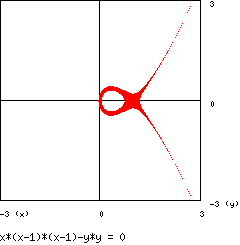
                        (il punto (1 , 0) appare ingrandito a causa dell’approssimazione
                        numerica utilizzata)

        - 5 -         parabola cuspidata :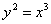

                        il grafico è :



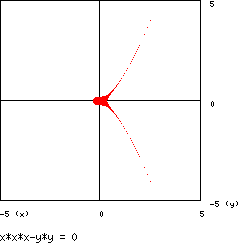
                        (il punto (0 , 0) appare ingrandito a causa dell’approssimazione
                        numerica utilizzata)

Curve trascendenti notevoli in R²

Elenchiamo qui alcune curve trascendenti notevoli in R².

01 – Sinusoide.

Nel piano cartesiano, la curva trascendente :



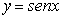
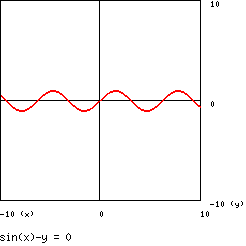
è detta sinusoide ed il suo grafico è :



02 – Tangentoide.

Nel piano cartesiano, la curva trascendente :



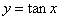
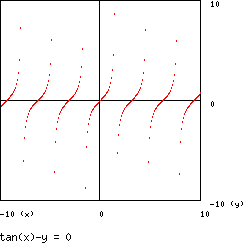
è detta tangentoide ed il suo grafico è :



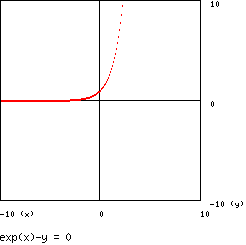
03 – Esponenziale.

Nel piano cartesiano, la curva trascendente :



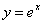
dove e ≈ 2,718 … è il numero di Nepero, è detta curva esponenziale ed il suo grafico
è :



04 – Gaussiana.

Nel piano cartesiano, la curva trascendente :



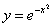
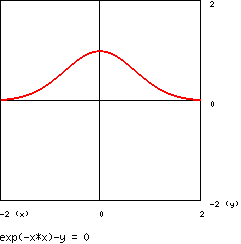
dove e ≈ 2,718 … è il numero di Nepero, è detta curva gaussiana o curva degli
errori ed il suo grafico è :



05 – Spirale di Archimede.

Nel piano cartesiano, la curva trascendente in coordinate polari :



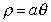
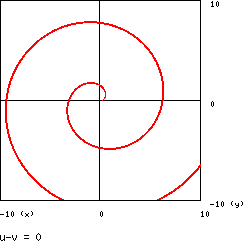
dove a è un numero positivo, è detta spirale di Archimede. Nel caso in cui a = 1
il grafico è :



06 – Spirale iperbolica.

Nel piano cartesiano, la curva trascendente in coordinate polari :



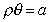
dove a è un numero positivo, è detta spirale iperbolica. Nel caso in cui a = 1 il grafico
è :



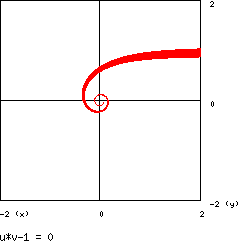
La spirale risulta amplificata a causa dell’approssimazione numerica usata. La spirale
iperbolica si avvolge indefinitamente attorno all’origine O e tende asintoticamente
alla retta y = a .

Superficie in R³

01 – Definizioni.

Consideriamo lo spazio euclideo R³ dotato di un sistema di assi cartesiani ortogonali Oxyz .
Esso sarà chiamato d’ora in poi più semplicemente spazio cartesiano. L’equazione :



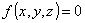
dove   f   è una funzione reale continua definita su un opportuno dominio di   x , y e z ,
rappresenta l’equazione di una superficie i punti della quale soddisfano l’equazione data.

Esempio :

        x ² + y ² + z ² - R ² = 0   è l’equazione di una sfera di centro O e raggio R



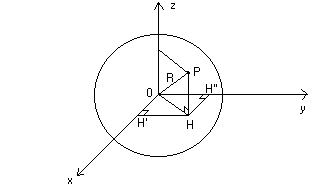
        in quanto ogni punto   P(x , y , z)   della sfera è tale per cui applicando il teorema
        di Pitagora ai triangoli rettangoli OHH’ e OHP ottenuti proiettando il punto P
        sugli assi cartesiani come indicato in figura si ottiene OH’² + H’H ² + PH ² = R ²
        e quindi, sostituendo OH’ = x , H’H = OH’’ = y e HP = z , si ha verificata
        l’equazione.

Risolvendo (ove possibile) l’equazione di una superficie rispetto ad una variabile, per
esempio la   z , si ottiene :



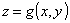
Questa è l’equazione della medesima superficie in forma esplicita.

L’equazione in forma esplicita della sfera dell’esempio precedente risulta essere
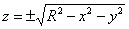(si noti che questa equazione non è una funzione perché per
un dato valore di   x e y , la   z assume due valori).

Se la funzione 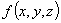è un polinomio in   x , y e z , la superficie si dice algebrica
ed il grado del polinomio si dice ordine della superficie, in caso contrario la superficie
si dice trascendente.

Le superficie algebriche del primo ordine sono le superficie di equazione .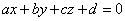
Esse sono i piani dello spazio.

Le superficie algebriche del secondo ordine sono dette quadriche.

Se l’equazione di una superficie è esprimibile come prodotto di due o più funzioni
α , β , … , cioè è del tipo 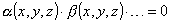, allora la superficie è
composta dalle superficie α = 0 , β = 0 … perché un prodotto è nullo quando è nullo
uno dei suoi fattori. In questo caso la superficie si dice riducibile, altrimenti si dice
irriducibile.

02 –Equazione parametrica.

L’equazione di una superficie può essere posta nella forma :



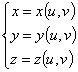
dove   u e v sono due parametri reali compresi fra due valori prefissati ( a ≤ u ≤ b ,
c ≤ v ≤ d , dove a e c possono essere anche -∞ e b e d possono essere anche
+∞ ) ed   x(u , v) , y(u , v) , z(u , v) sono tre funzioni reali continue. Una superficie
così definita si dice espressa in forma parametrica.

Perché il suddetto sistema rappresenti veramente una superficie occorre anche che
la matrice Jacobiana :



abbia rango 2 in tutto il dominio di validità dei parametri u e v . In caso contrario,
il sistema rappresenta una curva. Per esempio, il sistema 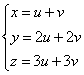, il cui Jacobiano
è   in quanto intersezione dei piani
y = 2x e z = 3x (basta sostituire u + v = x nella seconda e nella terza equazione).

Per passare dalla forma parametrica alla forma esplicita, è sufficiente ricavare un parametro
(ove possibile) da una delle tre equazione e sostituirlo nelle altre due, poi ricavare l’altro
parametro da una di queste ultime e sostituirlo nell’altra.

Viceversa, per passare dalla forma esplicita z = g(x , y) alla forma parametrica è sufficiente
porre   x = u , y = v e   z = g(u , v) con   u e v   definiti su gli stessi valori in cui sono definiti
x e y . Si noti che le forme parametriche di una superficie sono infinite, in quanto i parametri
possono essere scelti arbitrariamente.

Esempi :

        -1 - 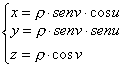         , con 0 ≤ u ≤ 2π , 0 ≤ v ≤ π , rappresenta una
                        sfera di centro O e raggio   ρ .

                        Infatti, elevando al quadrato i tre membri e sommando membro a membro,
                        si ottiene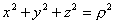

        - 2 -         z = x ² + 2xy – 1   è una quadrica in forma esplicita. Una sua forma
                        parametrica è .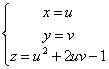

04 – Coordinate cilindriche e sferiche.

La scelta delle coordinate cartesiane ortogonali non è l’unica possibile. Nello spazio è
possibile scegliere infiniti sistemi di riferimento di cui quello cartesiano ortogonale è
sicuramente il più semplice da utilizzare in un grande numero di applicazioni concrete.

Un sistema di coordinate non cartesiane molto importante è il sistema delle coordinate
cilindriche. Esso è definito rispetto ad un usuale sistema di riferimento cartesiano :



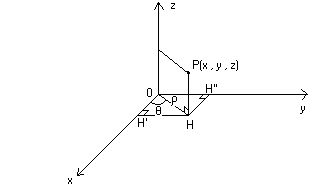
Se il punto   P ha coordinate cartesiane   (x , y , z) , la tripla ordinata (ρ , θ , z)
rappresenta le coordinate cilindriche del punto   P .

La coordinata ρ è il raggio vettore e può variare da   0 all’infinito. La coordinata
θ è l’ anomalia che viene misurata in senso antiorario rispetto al semiasse positivo
Ox e può variare da   0 a   2π. La coordinata z si chiama quota. Il punto   O   si
chiama polo e la semiretta   Ox   si chiama asse polare. Le coordinate cartesiane
in funzione delle coordinate cilindriche sono date dalle relazioni :



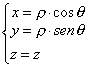
La relazione che esprime le coordinate cilindriche in funzione di quelle cartesiane è :



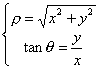
la prima si ricavano elevando al quadrato i primi due membri della precedente e
sommando, la seconda, dividendo i suddetti membri.

Si noti che, mentre   ρ è ricavabile direttamente, θ è ricavabile tramite la sua
tangente. Se si desidera utilizzare la funzione arcotangente, occorre notare che il
codominio della suddetta è definito fra - π/2   e   + π/2 .

Esempi :

        - 1 -         la quadrica   x² + y² - 1 = 0 diventa in coordinate cilindriche ρ² - 1 = 0 .
                        Si tratta evidentemente di un cilindro circolare di raggio 1 con asse
                        coincidente con l’asse Oz.



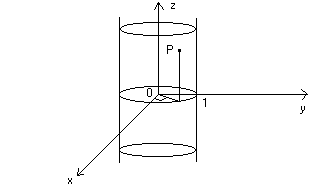
        - 2 -         la quadrica   x² + y² - z² = 0 diventa in forma polare ρ² - z² = 0 ovvero
                        ρ = ± z che corrisponde ad un cono circolare retto con vertice in O ed
                        asse coincidente con l’asse Oz.



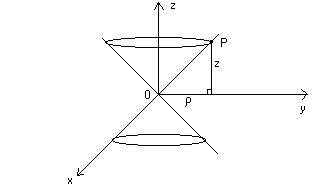
Un altro importante sistema di riferimento non cartesiano è costituito dalle coordinate
sferiche. Esso è definito rispetto ad un usuale sistema di riferimento cartesiano :



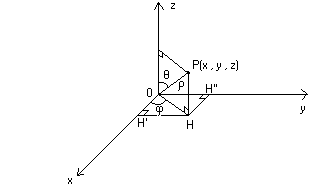
Se il punto   P ha coordinate cartesiane   (x , y , z) , la tripla ordinata (ρ , θ , φ)
rappresenta le coordinate sferiche del punto   P .

La coordinata ρ è il raggio vettore e può variare da   0 all’infinito. La coordinata
φ è la longitudine che viene misurata in senso antiorario rispetto al semiasse positivo
Ox e può variare da   0 a   2π. La coordinata θ è la colatitudine e può variare da
0 a   π. Il punto   O   si chiama polo e l’asse   Oz   si chiama asse polare. Il semipiano
appartenente al piano xz e contenente il semiasse positivo Ox si chiama semipiano
polare.

Le coordinate cartesiane in funzione delle coordinate sferiche sono date dalle relazioni :



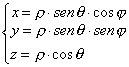
La relazione che esprime le coordinate sferiche in funzione di quelle cartesiane è :



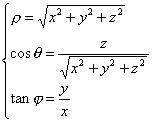
Esempio :

            -           la sfera   x ² + y ² + z ² - R ² = 0   diventa in coordinate sferiche
                        ρ² = R² ovvero ρ= R .

05 – Superficie notevoli.

Elenchiamo qui alcune superficie notevoli.

            - 1 -     piano

                        l’equazione di un generico piano è :



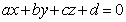
                        dove a , b , c , d sono numeri reali. Il piano x = k è un piano
                        perpendicolare all’asse Ox . Il piano   y = k è un piano perpendicolare
                        all’asse Oy . Il piano z = k è un piano perpendicolare all’asse Oz .

                        Se d = 0 il piano passa per O . In questo caso l’equazione del piano
                        può essere scritta usando il formalismo del prodotto interno :

                                <(x , y , z) , (a , b , c)> = 0 .

                        Questa forma è molto utile per le sue implicazioni geometriche. Essendo
                        il prodotto interno nullo, ciò significa che i vettori   (x , y , z) e   (a , b , c)
                        sono perpendicolari ovvero che il piano passante per O è l’insieme dei
                        vettori (x , y , z) perpendicolari ad un vettore fisso dato (a , b , c) .
                        Il vettore (a , b , c)   rappresenta quindi il “versore” del piano passante
                        per O :



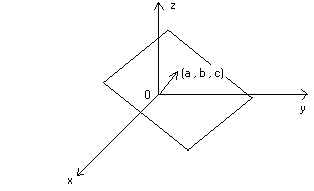
                        Nel caso di un piano non passante per O l’equazione del piano può
                        essere scritta con lo stesso formalismo come :

                                <(x , y , z) , (a , b , c)> = a² + b² + c²

                        che rappresenta un piano perpendicolare al vettore (a , b , c) e passante
                        per il punto (a , b , c) (omettiamo la dimostrazione) :



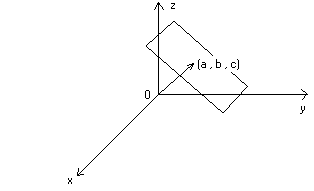
                        Con questo formalismo è molto semplice dedurre le condizioni di
                        parallelismo e perpendicolarità fra piani. Due piani sono paralleli
                        se hanno il medesimo versore. Due piani sono perpendicolari se i
                        loro versori sono perpendicolari ovvero il loro prodotto interno è nullo.

                        Il piano espresso in forma parametrica ha la seguente rappresentazione
                        (omettiamo la dimostrazione) :



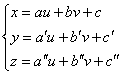
                        Il piano generico passante per il punto (a , b , c) ha equazione :



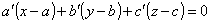
                        dove a’ , b’ , c’ sono numeri reale (omettiamo la dimostrazione).

                        Due piani di equazione ax + by +cz + d = 0 e a’x + b’y +c’z + d’ = 0
                        sono paralleli se vale la relazione (omettiamo la dimostrazione):



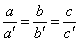
        - 2 -         sfera

                        la quadrica di equazione x² + y² + z² + αx + βy + γz + δ = 0 , dove
                        α, β, γ, δ sono numeri reali, rappresenta l’equazione di una sfera di
                        centro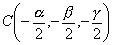
                        (omettiamo la dimostrazione). Naturalmente, occorre che il radicando
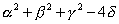                          sia positivo o nullo.

                        La rappresentazione parametrica della sfera di centro C(a , b , c) e
                        raggio R è 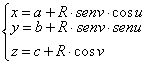  con 0 ≤ u ≤ 2π , 0 ≤ v ≤ π .

        - 3 -         cilindro

                        l’equazione f(x , y) = 0 (in cui manca la variabile z ) rappresenta una
                        superficie che, sezionata con piani z = k , presenta sezioni identiche alla
                        curva f(x , y) = 0 disegnata sul piano Oxy (piano di equazione z = 0).
                        Una siffatta superficie si chiama cilindro. Graficamente :



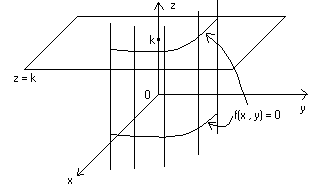
            - 4 -     cono

                        data l’equazione f(x , y) = 0 , che sul piano Oxy (piano di equazione
                        z = 0) rappresenta una curva, ed un punto 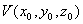, l’insieme
                        delle rette che passano per V e per ogni punto della curva data si
                        chiama cono di vertice V . Graficamente :



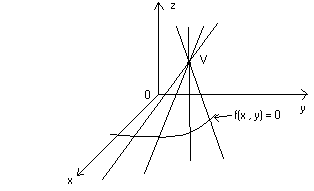
                        L’equazione del cono così definito è (omettiamo la dimostrazione) :



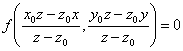
                        Esiste un’altra definizione di cono. Sia f(x , y , z) una funzione omogenea
                        di grado n ovvero tale che 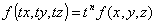allora la superficie
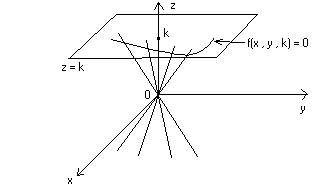
                        f(x , y , z) = 0 rappresenta un cono di vertice nell’origine O . Intersecando
                        il cono con un piano parallelo al piano Oxy (di equazione z = k) si ottiene
                        la curva di equazione f(x , y , k) = 0 rispetto al medesimo piano. Graficamente :

Curve in R³

01 – Definizioni.

Consideriamo lo spazio euclideo R³ dotato di un sistema di assi cartesiani ortogonali Oxyz .
Esso sarà chiamato d’ora in poi più semplicemente spazio cartesiano. Il sistema di due
superficie :



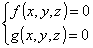
dove   f e g   sono due funzioni reali continue definite su un opportuno dominio di   x , y
e z , rappresenta una curva, che è appunto l’intersezione fra le due superficie, i punti
della quale soddisfano il sistema dato.

Esempio :

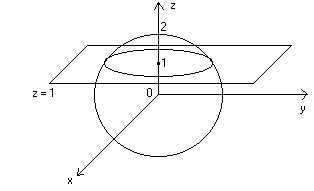
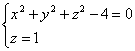          è la circonferenza intersezione della sfera di raggio 2 e centro
        in O con il piano perpendicolare all’asse Oz passante per (0 , 0 , 1) :



L’intersezione fra due superficie può dare luogo a più curve distinte. Le curve che non
interessano sono dette curve residue.

Se una curva giace su di un piano essa viene detta curva piana (come nell’esempio),
altrimenti viene detta curva sghemba.

02 –Equazione parametrica.

L’equazione di una curva può essere posta nella forma :



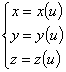
dove   u è un parametro reale compreso fra due valori prefissati ( a ≤ u ≤ b , dove a
può essere anche -∞ e b può essere anche +∞ ) ed   x(u) , y(u) , z(u) sono tre
funzioni reali continue. Una curva così definita si dice espressa in forma parametrica.

Per passare dalla forma parametrica alla forma definita al punto precedente, è sufficiente
ricavare un parametro (ove possibile) da una delle tre equazione e sostituirlo nelle altre
due.

Viceversa, per passare alla forma parametrica è sufficiente porre   x = u e ricavare, se
possibile, dal sistema 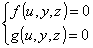la y e la z in funzione di u . Si noti che le forme
parametriche di una curva sono infinite, in quanto il parametro può essere scelto
arbitrariamente.

03 – Coordinate curvilinee.

La rappresentazione parametrica di curve e superficie ha importantissime e fondamentali
implicazioni che costituiscono il punto di partenza per il calcolo tensoriale (detto anche
calcolo differenziale assoluto). Il calcolo tensoriale, a sua volta, costituisce la base
matematica di fondamentali teorie fisiche quali la teoria della relatività.

Consideriamo la superficie S di equazione parametrica 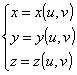  . Il punto P della
superficie S corrispondente ai valori 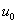  dati ai parametri   u e v è rappresentato
biunivocamente (sotto opportune condizioni) dalla coppia ordinata 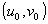. Cioè, le
coordinate cartesiane di P , 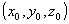  e
viceversa in quanto vale 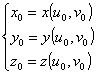(il viceversa non è vero in generale, ma lo
diventa prendendo una opportuna restrizione della funzione da R² a   R³ rappresentata
dall’equazione parametrica della superficie).

La coppia 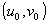  rappresenta allora le coordinate del punto P rispetto al sistema
di coordinate curvilinee u , v . Le coordinate u e v sono dette curvilinee perché
il punto P è l’intersezione delle curve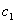
e 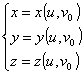   , che sono contenute completamente nella superficie S , ottenute
ponendo 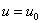. Graficamente :


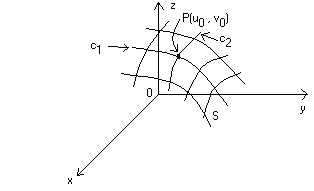
Esempi di coordinate curvilinee (le coordinate curvilinee sono qui tracciate per punti) :

            - 1 -     sfera :


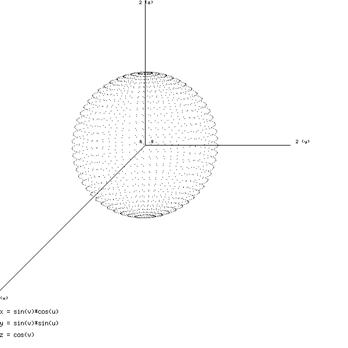
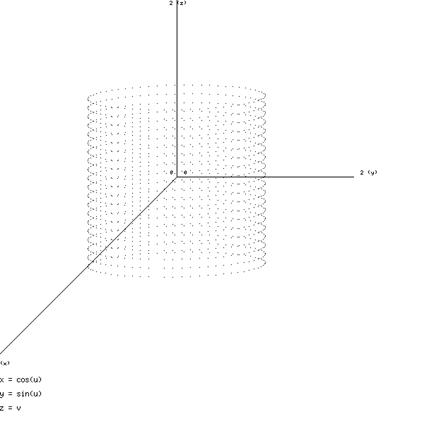
            - 2 -     cilindro :


04 – Curve notevoli.

Elenchiamo qui alcune curve notevoli.

            - 1 -     retta

                        l’equazione parametrica di una generica retta è :



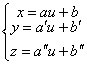
        - 2 -         elica circolare

                        l’equazione parametrica dell’elica circolare è :



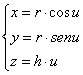
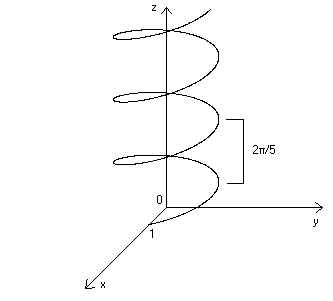
                        dove il parametro u varia da 0 a +∞ . Il numero r rappresenta il
                        raggio dell’elica ed 2πh rappresenta il “passo” dell’elica. Graficamente,
                        nel caso di r = 1 ed h = 1/5 :