• 
• 

 

Circonferenza e cerchio

 

 

---

 

Circonferenza e cerchio

 

I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

Circonferenza e cerchio

Passiamo ad esaminare alcuni nodi concettuali e le molte difficoltà che, a mio parere, gli studenti incontrano nello studio di questo argomento:

• dissonanza tra il linguaggio comune  e quello matematico: spesso usiamo il termine “disco” per indicare il cerchio matematico e “cerchio” per indicare la circonferenza

 

Definizione di circonferenza: è l’insieme dei punti del piano che hanno distanza fissa r da un punto assegnato O, detto centro.
Definizione di cerchio: è l’insieme dei punti del piano che hanno distanza minore o uguale a r da un punto assegnato O, detto centro.

 

Esercizio
La circonferenza è una figura concava o convessa? Concava

Esercizio
Il cerchio è una figura concava o convessa? Convessa

Esercizio
Quante circonferenze passano per un punto? Per due? Per tre?
Per un punto e per due punti passano infinite circonferenze. Per tre punti: dipende. Se non sono allineati passa una e una sola circonferenza, il cui centro è l’intersezione degli assi dei segmenti aventi per estremi due dei punti assegnati. Se sono allineati non passa alcuna circonferenza, poiché gli assi dei segmenti sono tra loro paralleli.

Esercizio
Quante cerchi passano per un punto? Per due punti? Per tre punti?  Come può essere interpretata la domanda?

Esercizio
Capovolgi un bicchiere, poggialo su un foglio e segna con la matita il suo bordo: hai disegnato una circonferenza. Trova il suo centro. Si può ritagliare il cerchio e con due piegature ad assi perpendicolari trovare il centro o disegnare due corde e trovare il punto di intersezione degli assi.

Si definiscono: corda, arco di circonferenza, settore circolare.

Data una circonferenza è importante la relazione che c’è tra il raggio, la lunghezza delle corde, la loro distanza dal centro. Per aiutare gli allievi a capire e ricordare questi importanti risultati è utile far produrre modelli di cartoncino di cerchi, sui quali siano indicati il centro e il raggio, che possano essere piegati per verificare sperimentalmente le relazioni che seguono.

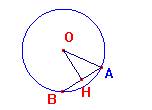
  -La distanza OH dal punto O alla corda AB la interseca nel suo punto medio.

• Ogni segmento che ha per estremi il centro O della circonferenza e il punto medio di una corda è ad essa perpendicolare.

 

• L’asse di una corda passa per il centro della circonferenza.

 

Si può applicare il teorema di Pitagora al triangolo rettangolo OAH per individuare uno dei tre lati, noti gli altri due.

Esercizio
Se una circonferenza ha raggio uguale a 3 cm, puoi tracciare una corda di 6 cm? E una di 8 cm?
Sì la corda di 6 cm è diametro, no quella di 8 cm perché è maggiore del diametro.

Esercizio
Una corda di una circonferenza di raggio 5 cm è lunga 6 cm. Trova la sua distanza dal centro.
Si applica il teorema di Pitagora. Una delle difficoltà degli alunni nel risolvere i semplici problemi che seguono sta nel rappresentare graficamente i dati. Spesso disegnano un raggio ma non è quello che permette di individuare il triangolo rettangolo OAH. La distanza è di 4 cm.

Esercizio
Una corda di lunghezza 24 cm dista dal centro 5 cm. Calcola il raggio della circonferenza.
Si applica il teorema di Pitagora. Il raggio è di 13cm

• Si può notare che, in una circonferenza, più la corda è lunga più si riduce la sua distanza dal centro.

 

• Corde parallele hanno i punti medi appartenenti allo stesso diametro

Esercizio
Se due corde sono parallele ed uguali, come risultano le loro distanze dal centro della circonferenza? Spiega la tua risposta aiutandoti anche con il disegno.

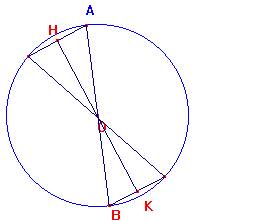
Si può misurare la lunghezza ed osservare che OH = OK o considerare i due triangoli OAH e OKB. Hanno  perché opposti al vertice, perché metà di segmenti congruenti, perché raggi della stessa circonferenza. Sono congruenti per uno dei criteri di congruenza dei triangoli rettangoli, quindi OH e OK sono congruenti. L’ipotesi di parallelismo è indispensabile per asserire che i punti H, O, K , e A, O,B sono allineati.

• Introduzione di nuovi termini: retta “secante”, “tangente”, “esterna ” ad una circonferenza. Scoperta del teorema:

  se d < r allora la retta è secante, se d = r la retta è   tangente, se d > r la retta è esterna (d è la distanza dal centro alla retta r il raggio della circonferenza).  
Esercizio
Disegna due rette perpendicolari. Dove deve essere situato il centro di una circonferenza che sia tangente contemporaneamente ad entrambe le rette? Di queste circonferenze ne esiste una sola? Ne esistono un numero finito o infinito? Rispondi aiutandoti con il disegno.
Esistono infinite circonferenze aventi il centro sulla bisettrice di uno degli angoli formati  dalle due rette.

Esercizio
Indica per ciascuna delle rette della figura se è secante, tangente o esterna alla circonferenza data.

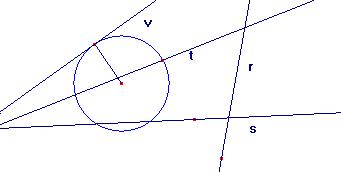
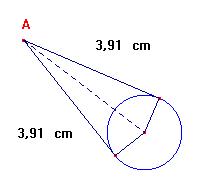
        Segmenti di tangenza condotti per uno stesso punto ad una  circonferenza sono congruenti.

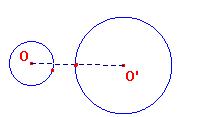
• padronanza e memorizzazione di nuovi termini : “secante”, “tangente”, “esterno a”, riguardanti la posizione reciproca di due circonferenze e le relazioni metriche che legano OO’ e i raggi.

 
Non credo che sia utile memorizzare le relazioni tra i centri OO’ e i raggi, ma saper ragionare nei casi specifici.

Esercizio
Associa a ciascuna relazione la figura corrispondente.
a.   OO’ = r + r’     b. OO’ > r + r’    c. OO’ = r - r’     d. OO’ < r - r’  e. OO’ < r + r’      
1. 2. 3  

          .

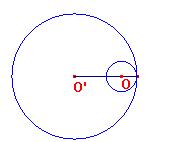
•                                                             5.

a e2  - b e 1  - c e 4 – d e 5 – e e 3.

Esercizio
Due circonferenze sono tangenti esternamente  e hanno distanza tra i centri di 12 cm. Se il raggio di una è doppio di quello dell’altra, calcola la lunghezza dei due raggi.

Esercizio
Due circonferenze sono tangenti internamente e i loro centri distano 8 cm. Calcola la lunghezza dei raggi, sapendo che uno è il quintuplo dell’altro.
Questi due esercizi si possono risolvere con il metodo grafico, impostando le proporzioni (nel primo caso si applica il comporre, nel secondo lo scomporre) o con le equazioni.
Individuazione di angoli al centro e alla circonferenza che insistono su un assegnato arco e relazione
tra le loro ampiezze

 

DEFINIZIONE di angolo al centro : data una circonferenza si dice angolo al centro ogni angolo che  ha  il vertice nel centro della circonferenza (sarebbe meglio specificare: ogni angolo complanare con la circonferenza)

DEFINIZIONE di angolo alla circonferenza: data una circonferenza si dice angolo alla circonferenza ogni angolo con il vertice sulla circonferenza e i lati entrambi secanti oppure uno secante e uno tangente.

Difficoltà a rappresentare graficamente un angolo al centro, assegnato un angolo alla circonferenza e viceversa

• Difficoltà a lavorare con angoli alla circonferenza con un lato secante e l’altro tangente
• Relazione tra un angolo al centro e gli angoli alla circonferenza che insistono sullo stesso arco.

Qui occorre dedicare un po’ di tempo alle rappresentazioni grafiche, i teoremi possono essere memorizzati più facilmente se c’è una verifica sperimentale, usando il compasso, il goniometro, la carta trasparente.  Se la classe segue bene si può proporre la dimostrazione. Da evidenziare che un angolo che insiste su una semicirconferenza è retto.

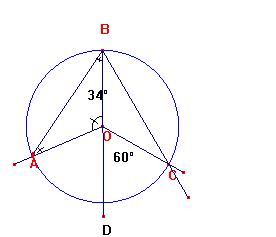
Esercizio
Determina le ampiezze degli angoli dei triangoli ABO e BOC.

E’utile affrontare questa parte? Sì, se si vuole giustificare che alcuni quadrilateri convessi sono inscrittibili in una circonferenza ed altri no.
Introduzione di p: si può richiedere agli alunni di produrre cerchi di cartoncino di raggi diversi o di considerare modelli di solidi che hanno per base un cerchio (lattine,  CD, ecc) e, servendosi di un metro da sarta (flessibile), si rileva la lunghezza del diametro e della circonferenza. Si invitano gli alunni a calcolare il rapporto tra la lunghezza di ogni circonferenza e il relativo diametro. Si può fare la media aritmetica tra i valori registrati dagli allievi e scoprire che questo valore è costante e viene indicato con p.
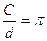 Già in questa uguaglianza c’è una difficoltà legata alla divisione e al concetto di   rapporto.

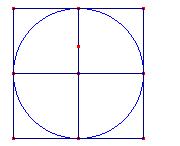
Un altro metodo consiste nell’osservare diverse circonferenze aventi raggio  doppio,  triplo,     quadruplo,.. di una di raggio assegnato e notare che anche la lunghezza delle circonferenze raddoppia, triplica,.. Chiamato 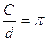 si cerca di stabilire il valore di p considerando il quadrato circoscritto ad una circonferenza (ha tutti i lati tangenti alla circonferenza)

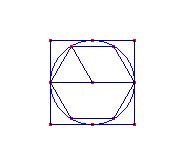
e l’esagono regolare inscritto. Risulta: 8r > C > 6r. Per cui 4 > p > 3.
Aumentando il numero dei lati e considerando i perimetri dei poligoni regolari inscritti e circoscritti si può ottenere una migliore approssimazione.

• Difficoltà a comprendere la ”natura” di p: nel corso dei secoli si sono utilizzate diverse approssimazioni; solo nel 1882, grazie a Lindemann, si ha la dimostrazione che p è trascendente (l’irrazionalità era già stata dimostrata); p ha infinite cifre dopo la virgola ed esse non si ripetono periodicamente, inoltre non è soluzione di alcuna equazione algebrica a coefficienti interi. Non si può esprimere mediante radici quadrate. Con questa dimostrazione si mette il punto fermo alla questione: è possibile quadrare un cerchio con gli strumenti riga e compasso? NO. Questo per noi equivale a dire che non si può rappresentare p sulla retta reale con i soliti strumenti. Dunque è errore asserire che p = 3,14. Meglio utilizzare anche nelle formule p, quando ciò è possibile o specificare p   3,14.
• Formula: C = 2 p r e formula inversa

La difficoltà è legata alla scarsa padronanza delle proprietà delle operazioni: non sempre è chiaro perché dato r = 4 cm è possibile scrivere C = 8 p cm, mettendo il p prima dell’unità di misura.

Esercizio
La somma delle lunghezze di due circonferenze è 14p m e una è 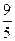 dell’altra. Calcola la lunghezza dei loro raggi.
Si può risolvere con il metodo grafico, impostando una proporzione o un’equazione. .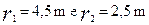

• Calcolo dell’area della superficie del cerchio: un’esperienza estremamente utile è quella di realizzare modelli di cerchi di materiale diverso (compensato, cartone pressato, plexiglass) aventi il raggio , per esempio di 5cm, 10 cm e 15 cm e modelli di quadrati dello stesso materiale, aventi il lato uguale al raggio dei cerchi. Avendo a disposizione una bilancia digitale si possono pesare i cerchi e i quadrati e scoprire che .

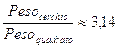Supponendo che ai modelli di cerchio e quadrato corrispondano lo stesso spessore e lo stesso peso specifico si può dedurre che a pesi uguali corrispondano superfici uguali, quindi .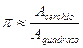

Altra possibilità è considerare i poligoni regolari circoscritti. All’aumentare del numero di lati l’area del poligono si avvicina sempre di più all’area del cerchio. A = 2pxa/2, sostituendo al posto di 2p 2pr, al posto di a r (raggio) e semplificando si ottiene A=pr2 .
Esercizio
Calcola la lunghezza del diametro di un cerchio di area 289 pcm2 .
La difficoltà sta nell’utilizzare la formula inversa. Quando si scrivono 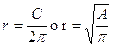è utile utilizzare gli schemi con le frecce ed invertire al ritorno le operazioni.

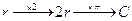
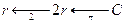
Esercizio
Due amici acquistano la pizza: Pino un trancio rettangolare avente il lato di 20 cm, Gino una pizza tonda, avente il raggio di 15 cm. Supposto che entrambi abbiano finito la loro porzione, chi ha mangiato quella più estesa?
Pino: 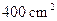, Gino più di . Ovviamente non serve , ai fini del problema, sostituire il valore 3, 14 o tenere !

• memorizzazione delle formule sopra menzionate: in entrambe le formule compaiono 2, r, p, ma sono legati tra loro da operazioni diverse. In 2 p r compaiono due moltiplicazioni, in p r2 c’è un elevamento al quadrato e una moltiplicazione. Non considerando l’unità di misura spesso gli allievi non percepiscono che la seconda formula si riferisce all’area di una superficie. Inoltre, poiché hanno difficoltà a padroneggiare le proprietà delle operazioni, non capiscono perché in 2 p r se si sostituisce a r il valore 4 cm si può spostare p in fondo e scrivere 8p cm.
• Si possono poi trattare:

 

il legame tra ampiezza angolo al centro, area di un settore circolare: proporzioni, formula per area settore (utile per calcolare l’area laterale di un cono), uso in statistica per la rappresentazione di dati mediante aerogrammi.

p day: festeggiamenti per un numero così importante!

Il 14 marzo (3-14) di ogni anno!

 

fonte: http://www-3.unipv.it/iscr/corsi_speciali/dispense/matematica/vettorello/circonferenza%20e%20cerchio%20barbara.doc

sito web: http://www-3.unipv.it/

 

Autore del testo: Barbara

 

 

 

Circonferenza e cerchio

 

 

Circonferenza e cerchio

 

Disclaimer

Questo sito non rappresenta una testata giornalistica e viene aggiornato senza alcuna periodicità, esclusivamente sulla base della disponibilità del materiale, pertanto non è un prodotto editoriale sottoposto alla disciplina di cui all'art. 1, comma III della Legge n. 62 del 7.03.2001. I riassunti , gli appunti i testi e le citazioni contenuti nel nostro sito sono messi a disposizione gratuitamente a studenti, ricercatori, professori, tecnici con scopi illustrativi didattici e scientifici con il concetto del fair use e con obiettivo del rispetto della direttiva europea 2001/29/CE e della legge n. 633 art. 70 e dlg 68. Il sito è curato e coordinato dall’autore al solo scopo informativo e didattico. Pur ritenendo le fonti utilizzate affidabili, l'autore di questo sito non garantisce l'accuratezza e l'integrità delle informazioni contenute e pertanto declina ogni responsabilità per eventuali problemi o danni causati da errori o omissioni, nel caso tali errori o omissioni risultino da negligenza, caso fortuito o altra causa. Tutti gli appunti, le citazioni i testi e le immagini , sono proprietà dei rispettivi autori o case di produzione che ne detengono i diritti, qualora gli aventi diritto si ritenessero danneggiati dall'inserimento in questo sito dei predetti files o fossero stati inavvertitamente inseriti immagini, informazioni, testi od altro materiale coperto da Copyright saranno immediatamente rimossi e/o ne saranno citate le fonti su semplice segnalazione all' indirizzo e-mail indicato nella pagina contatti .

Gli obiettivi di questo sito sono il progresso delle scienze e delle arti utili in quanto pensiamo che siano molto importanti per il nostro paese i benefici sociali e culturali della libera diffusione di informazioni utili. Tutte le informazioni e le immagini contenute in questo sito vengono qui utilizzate esclusivamente a scopi didattici, conoscitivi e divulgativi. Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione). In questo sito abbiamo fatto ogni sforzo per garantire l'accuratezza dei tools, calcolatori e delle informazioni, non possiamo dare una garanzia o essere ritenuti responsabili per eventuali errori che sono stati fatti, i testi utilizzati sono stati prelevati da siti che li hanno messi a disposizione gratuitamente per farli conoscere nel web con scopi didattici. Se trovate un errore su questo sito o se trovate un testo o tool che possa violare le leggi vigenti in materia di diritti di autore, comunicatecelo via e-mail e noi provvederemo tempestivamente a rimuoverlo.

 

---

 

---

 

Designed by Larapedia.com 1998 -2011