luoghi geometrici

 

 

luoghi geometrici

 

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

 

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

 

 

 

 

luoghi geometrici

 

LUOGHI GEOMETRICI

Si definisce LUOGO GEOMETRICO   l’insieme di tutti e soli  i punti P (  del piano o dello spazio) che  godono di una  certa proprietà R

ovvero

affermare che una figura F  è  luogo geometrico dei punti  che godono della proprietà R   equivale a scrivere

P è un punto di F ó P gode della proprietà R

Il concetto di luogo geometrico è pertanto fondamentale in  Geometria in quanto  permette  una connessione logica tra due proprietà

  • P appartiene ad una figura F
  • P soddisfa una certa relazione  R

La prima è una proprietà geometrica, la seconda può anche essere espressa in linguaggio algebrico

Ricordiamo in proposito , la definizione   delle  Coniche come luoghi geometrici piani

Circonferenza di centro C e raggio r : luogo geometrico dei punti del piano  aventi  tutti distanza  da C uguale ad r  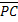®   =r

Parabola : luogo geometrico dei punti del piano  equidistanti da un punto fisso  F detto fuoco e da una retta fissa d, detta direttrice ®

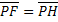  , dove H è il piede della perpendicolare condotta da  P a d

Ellisse di asse maggiore 2a: luogo geometrico dei punti del piano  per i quali la somma delle distanze da due punti fissi , F1 ed F2,detti fuochi ,  ha un valore costante , uguale a 2a®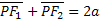

Iperbole di asse trasverso 2a :luogo geometrico dei punti del piano  per i quali il modulo della differenza  delle distanze da due punti fissi, F1 ed F2,detti fuochi ,ha un valore costante , uguale a 2a®

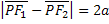
Il metodo delle coordinate  permette di tradurre ciascuna delle precedenti relazioni in un’equazione algebrica  nelle due variabili  x ed y che caratterizza la curva , anzi si identifica con essa .

Equazioni canoniche (  in un  opportuno sistema di riferimento)

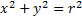  circonferenza

y= a x2+bx+c    parabola

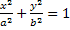  ellisse

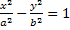 iperbole

Vedremo in seguito vari modi di definire un luogo geometrico ritrovando figure già note e familiarizzando con altre meno note nella geometria elementare

ESEMPI

  •  Asse di un segmento

Un noto teorema di Geometria elementare afferma che:<<L’asse di un segmento AB è il luogo geometrico dei punti del piano  equidistanti da A e da B>>

Ovvero

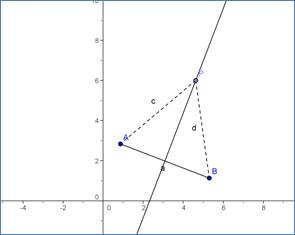
  • Se P è un punto dell’asse,      allora       
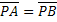
  • Viceversa : Se 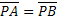            allora P appartiene all’asse

      In questo caso   

        F : asse del segmento AB (retta perpendicolare nel suo punto medio)

         R :  P è equidistante da  A e da B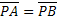 

Se nel piano è fissato un riferimento cartesiano Oxy e se le coordinate di A e B sono note, per esempio  A(1,3)  B(5,1),

la proprietà  R si traduce in una relazione tra le coordinate (x;y) del  generico punto P

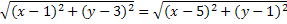
Svolgendo i calcoli si ottiene l’equazione    8x -4y-16=0

Fig1

 

Con i metodi della Geometria Analitica  possiamo  , viceversa,  riconoscere  che l’equazione trovata  corrisponde ad una retta perpendicolare al segmento AB e passante per il suo punto medio

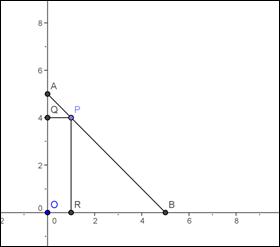  • E’ dato un angolo retto  avente per lati le semirette OX e OY.

Determinare all’ ’interno dell’ angolo il luogo dei punti tali che la somma delle distanze dai due lati sia minore di  5 unità.

 Risoluzione sintetica :

Consideriamo  un punto A sul lato OY e un punto B sul lato OX tali che i segmenti OA e OB abbiano entrambi lunghezza uguale  5

a)Dimostriamo   che il segmento AB , privato degli estremi, è  il luogo dei punti ( interni all’angolo retto)  tali che la somma delle distanze dai due lati sia uguale a  5 unità

Scegliamo un punto P interno al  segmento AB e costruiamo il rettangolo  OQRP: è facile osservare che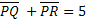

Infatti 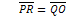 in quanto il triangolo AQP è rettangolo isoscele, essendo simile al triangolo AOB

Fig2

 

Viceversa :

Scegliamo un punto Q  sul lato OY e costruiamo il rettangolo  OQRP  dove il lato QP è lungo quanto il segmento AQ:

Per la similitudine dei triangoli AQP e AOB , iil vertice appartiene necessariamente al segmento AB

c)

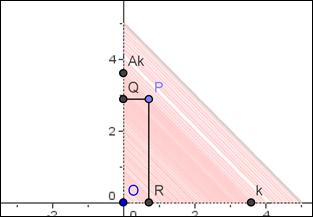
Pertanto il luogo richiesto è costituito da tutti e soli i punti interni al triangolo AOB

Fig.3

RISOLUZIONE ANALITICA

Scegliamo un riferimento cartesiano Oxy in modo che l’angolo retto assegnato ne costituisca il primo quadrante.

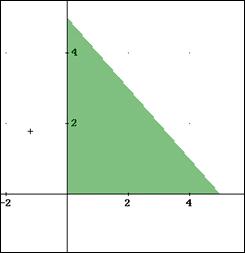
Il luogo è pertanto l’intersezione di tre semipiani: il semipiano delle x positive, il semipiano delle y positive, il semipiano  avente per origine la retta di equazione x+y=5 e contente il punto O

 

 

 

Fig.4

 

3)Un proiettile viene lanciato con  una velocità iniziale di componenti  vox e voy   rispettivamente. Determinarne la traiettoria

In un riferimento cartesiano avente l’origine nel punto  dove si trova inizialmente il proiettile, la posizione del punto  è associata  alla coppia di coordinate (x;y)

In un generico istante t devono valere le due relazioni

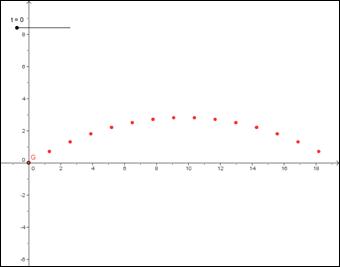
Il luogo geometrico  dei  punti P(x,y) che soddisfano le precedenti relazioni , è la TRAIETTORIA del proiettile.

In questo caso la proprietà R  è una relazione indiretta tra ascissa e ordinata del punto P, in quanto  ciascuna delle due coordinate è associata allo stesso valore del parametro t.

Le due equazioni rappresentano il luogo in forma parametrica, sono cioè                                                                 

le equazioni parametriche della traiettoria

 

Fig.5

 

Eliminando t tra le due equazioni si perviene all’equazione     y =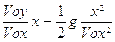

che rappresenta una  parabola

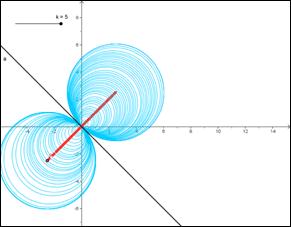4)E’ dato il fascio di circonferenze di equazione x2+y2+kx+ky=0

Determinare il luogo geometrico dei centri.

Risoluzione sintetica:

poiché le circonferenze sono tutte tangenti nell’origine  O alla stessa retta (  la bisettrice del secondo e quarto quadrante), il luogo dei centri è la retta perpendicolare in O alla tangente comune.

Infatti , in ciascuna circonferenza, congiungendo il centro C con O, si ottiene una retta perpendicolare alla tangente e, viceversa,  la retta per O perpendicolare alla tangente, passa per C.

Fig.6

 

Risoluzione analitica:

Il generico centro C ha coordinate ( -k/2;-k/2), pertanto le equazioni parametriche del luogo geometrico sono

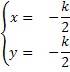
Eliminando il parametro  k si ottiene l’equazione cartesiana del luogo  y=x, che è proprio la perpendicolare alla tangente nell’origine

5)Un esempio di equazioni parametriche dipendenti da due parametri (vincolati da una relazione)

Determinare il luogo geometrico descritto dal punto medio di un segmento AB, di lunghezza 5,  mentre A <<scivola>> sul semiasse delle y positive  e B sul semiasse dellex positive  , mantenendo invariata la  lunghezza   di AB

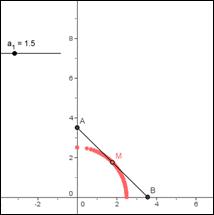
Sia A (0;α) e B(β;0) con le condizioni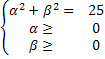    

Le coordinate  di M saranno  (β /2 ; α/2 )

Le equazioni parametriche del luogo sono pertanto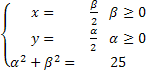 

Fig.7

Eliminando α e β  si trova

 

4x2+4y2=25  che rappresenta una circonferenza col centro nell’origine e raggio  5/2

Tenendo conto delle condizioni imposte il luogo richiesto  è   un quarto di circonferenza

 

COSTRUZIONE DI LUOGHI GEOMETRICI CON GEOGEBRA

Le figure degli esempi precedenti, ad eccezione della figura 4,  sono state eseguite  tutte con GEOGEBRA.

Per  la figura 4  è stato utilizzato  Derive,  dove è possibile risolvere graficamente  disequazioni e sistemi in  due variabili

STRUMENTI DI GEOGEBRA UTILI PER STUDIARE I LUOGHI GEOMETRICI

Vediamo ora come utilizzare Geogebra  per risolvere alcuni problemi sui luoghi geometrici o per visualizzarne le soluzioni.

  • Comando  <<LUOGO>> o modalità luogo 

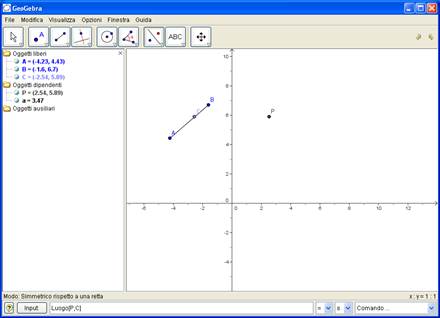
Si vuole visualizzare il luogo descritto dal punto P , collegato, nella costruzione , al punto C (in questo caso è il simmetrico di C rispetto all’asse y)

C deve  a sua volta essere vincolato a muoversi, su un oggetto (retta, circonferenza, funzione etc..) In questo caso C è vincolato sul segmento AB

  Si seleziona LUOGO dalla lista COMANDO, in basso a sinistra

 Nella barra di input compare Luogo[]

Inserire Luogo[P,C]  e premere INVIO

Compare il grafico del luogo , il segmento simmetrico di AB rispetto all’asse y

In alternativa :

Selezionare  la modalità LUOGO dal menù degli strumenti

Marcare il punto P e cliccare sul punto C

                                                                    ë

  •  Proprietà TRACCIA ON

            a)Selezionare il punto P col tasto destro del mouse, scegliere Proprietà

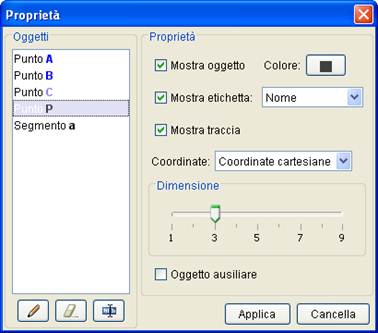              b)Selezionare MOSTRA TRACCIA ed eventualmente scegliere un colore

             c)Col puntatore muovere il punto C su AB

             d) P lascerà una  <<traccia>>, il grafico del luogo richiesto

 

 

 

 

 

 

 

 

 

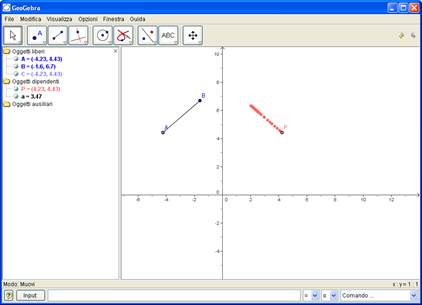
  •  Utilizzo di uno SLIDER per  tracciare il grafico di un luogo definito con le equazioni parametriche

Uno Slider è la rappresentazione grafica di un valore numerico generico  o di un angolo.

 

Si può variare il  valore trascinandolo, mediante il puntatore,   sul suo segmento rappresentativo

 

 

 

 

 

 

 

Si può creare uno Slider di qualunque variabile numerica dopo averla definita,  selezionandola col tasto destro e scegliendo <<mostra oggetto)

Oppure scegliendo la modalità nel menù degli strumenti

ë

 

Cliccando su un punto qualunque del foglio compare la finestra seguente

 

 

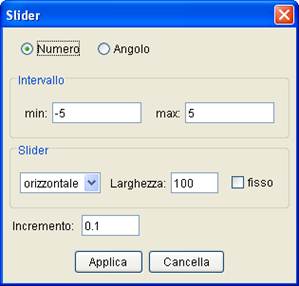
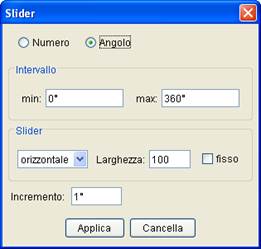
Le equazioni parametriche 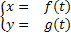    definiscono per ogni valore del parametro t,  le coordinate di un punto P.

  • Definire il punto P=(f(t), g(t)) 
  • costruire uno slider   dove far variare, mediante  il puntatore,  i valori t,  scegliendo opportunamente il minimo e il massimo
  • assegnare a P la proprietà << traccia on>> o > <<mostra traccia>>
  • trascinare il valore di t sullo slider

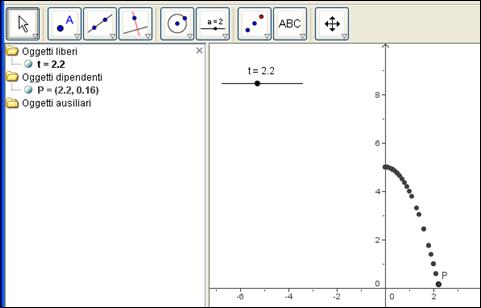Esempio P=(t,  5-t2)

 

 

 

 

 

 

 

 

 

1)LA PARABOLA

 Assegnati il punto   F  e la retta d, costruire il luogo dei punti del piano equidistanti da F e da d

Dal protocollo di costruzione si osserva che il punto  P  della figura seguente  soddisfa la relazione caratteristica del luogo.

Il grafico può essere evidenziato mediante il comando <<luogo>> o con >>Traccia on>>

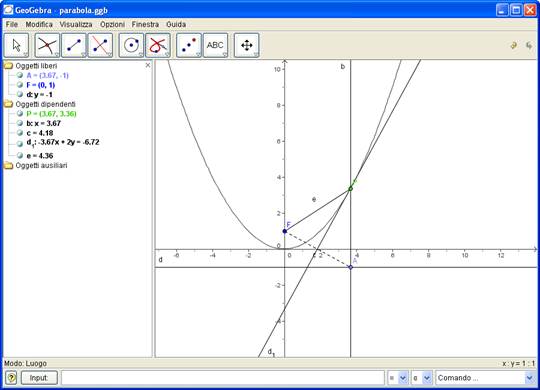
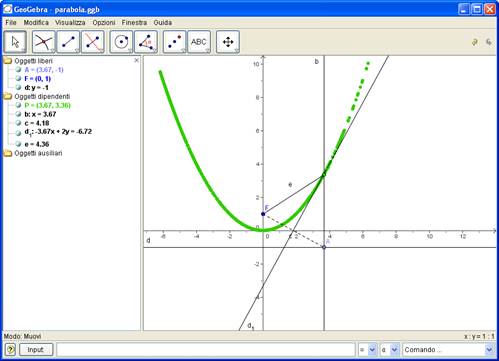
Utilizzando il comando Parabola[F,d] è possibile ottenere anche l’equazione (nella finestra Algebra)

2)L’ELLISSE

Assegnati due punti F1 ed F2 e un numero reale positivo a, costruire il luogo dei punti del piano tali   che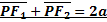       

 

Dal protocollo di costruzione si osserva che i punti F e G soddisfano la relazione caratteristica del luogo.

Il grafico può essere evidenziato mediante il comando <<luogo>> o con >>Traccia on>>

 

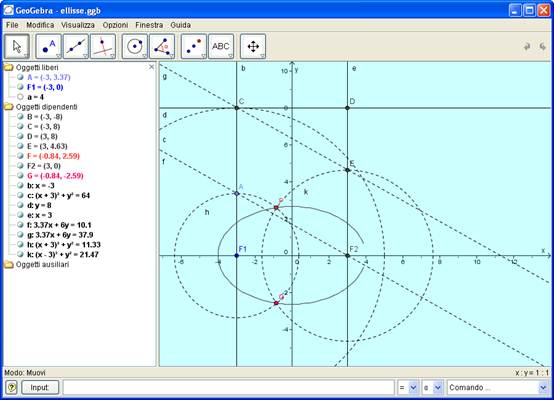
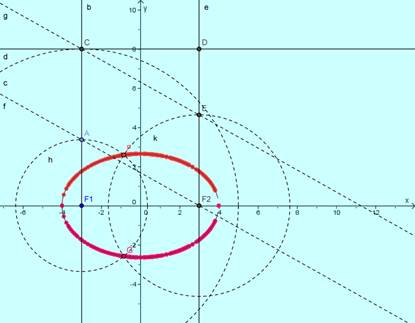
Utilizzando il comando Ellisse[F1,F2,a] è possibile ottenere anche l’equazione (nella finestra Algebra)

 

 

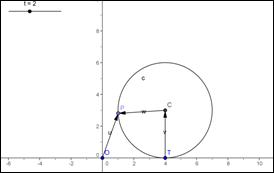
3)Baricentro di un triangolo

E’ data la circonferenza di diametro AB, dove A(-3;0) e B(3,0), la cui equazione è x2+y2=9.

Se C è un punto variabile sulla circonferenza, qual è il luogo descritto dal baricentro G del triangolo ABC?

Le coordinate del punto OP possono  essere poste nella forma (3cos α, 3 sen α)

Le coordinate di G saranno

 

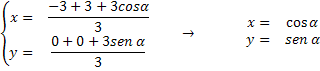
Quadrando e sommando membro a membro si ottiene l’equazione cartesiana del luogo richiesto   x2+y2= 1

 

Metodo sintetico

Si  costruisce G come punto di incontro di due delle mediane

              Si assegna a G la proprietà <traccia on>>

Si trascina C e si ottiene la <<traccia>> lasciata da G : una circonferenza col centro nell’origine e raggio 1

 

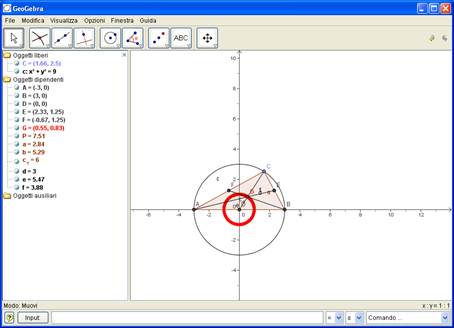
Metodo analitico

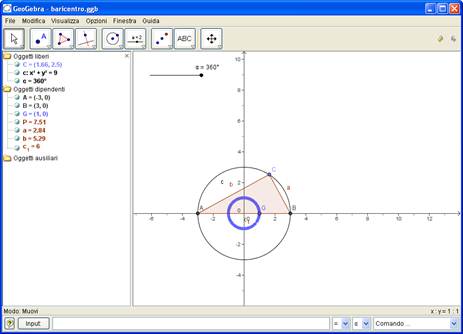
Si crea uno slider Angolo

Si definisce il punto G, secondo le equazioni parametriche

 Si assegna a G la proprietà <traccia on>>

Si fa variare α e si ottiene la <<traccia>> lasciata da G

 

 

 

ESERCIZI

1)Determinare il luogo geometrico dei punti equidistanti da due rette assegnate

a) nel caso in cui siano incidenti

b)nel caso in cui siano parallele

Risolvere il problema analiticamente , in un opportuno sistema di riferimento, ed eseguire la costruzione con Geogebra

2)Costruire l’iperbole come  luogo geometrico.

Fissati i fuochi e il semiasse maggiore, scriverne l’equazione e verificarla con il comando Iperbole[F1,F2,a]

3)Generalizzare  l’esempio 3  verificando che

Se due vertici  di un triangolo sono fissi  e il terzo varia su una circonferenza,su una retta o su una parabola, anche il baricentro del triangolo descrive rispettivamente una circonferenza, una retta, una parabola

Risolvere il problema analiticamente , in un opportuno sistema di riferimento, ed eseguire la costruzione con Geogebra

4)In un riferimento cartesiano Oxy sono dati i  punti A(4;0) e B(0;3)

Determinare il luogo geometrico dei punti del piano tali che l’area del quadrilatero convesso OAPB sia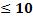

Risolvere il problema analiticamente, ed eseguire la costruzione con Geogebra

5)Verificare, analiticamente e graficamente, che le equazioni parametriche

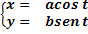
Definiscono un’ellisse.

 

ALCUNE  CURVE CELEBRI

Le Spirali

Galassia a spirale

La spirale, quella curva piana che ha la proprietà di avvolgersi in infiniti giri intorno ad un punto,  è nota sin dall’antichità Essa è una delle forme geometriche più diffuse in natura ed è presente come simbolo esoterico in varie culture.

Noi vogliamo, ovviamente,  evidenziarne le proprietà geometriche.

Studiamo, in particolare la spirale di Archimede e la spirale logaritmica

La spirale di Archimede

La spirale di Archimede, presentata dal sommo matematico siracusano nel 224 a.C., in un opera dedicata appunto alle spirali, è la traiettoria descritta  da un punto che si sposta uniformemente su una semiretta , mentre questa ruota a sua volta, uniformemente attorno al suo estremo.

La curva in pratica  è ottenuta tracciando una circonferenza in modo continuo ed aumentandone il raggio in modo proporzionale all'angolo percorso.

La sua equazione è molto semplice in  coordinate polari 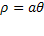  dove ρ è la distanza del punto rispetto  all’origine, θ l’angolo descritto dalla semiretta ,il parametro a una costante caratteristica della curva.

Le equazioni parametriche sono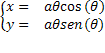

Applicazione cinematica

MOTO SU UNA PIATTAFORMA ROTANTE

Si consideri un riferimento spaziale Oxyz solidale con la terra.

Una piattaforma di centro O e raggio R ruota in senso antiorario con velocità angolare ω intorno all’asse z

Da O , nell’istante to=0,parte un punto materiale P  che si muove con velocità costante v = 2 m/s lungo l’asse x.

Studiare la traiettoria di P rispetto alla terna Oxyz  e rispetto ad una terna O’x’y’z’ solidale con la piattaforma , dove O’ coincide con O e z’ coincide con z.

(Si supponga che all’istante to le due terne cartesiane siano sovrapposte)

 

Consideriamo so il piano Oxy dove giace la piattaforma

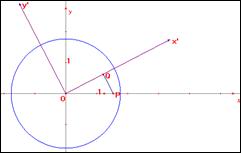In un istante t gli assi x’ e y’  hanno subito una rotazione di un angolo  ωt rispetto al riferimento terrestre

 

dove l’angolo 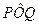è uguale a ωt

 

E’ facile verificare che, in un determinato istante t,  le coordinate di P sono

 

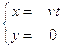  rispetto a Ox’y’ ( misure dei segmenti orientati OQ e QP, rispettivamente)

Se si inverte il senso di rotazione ω va sostituito con -ω

La traiettoria <<assoluta>> è  una retta , mentre quella  <<relativa>> è  una spirale di Archimede. L’osservatore non inerziale interpreta il fenomeno come l’effetto di una forza apparente , la forza di Coriolis.

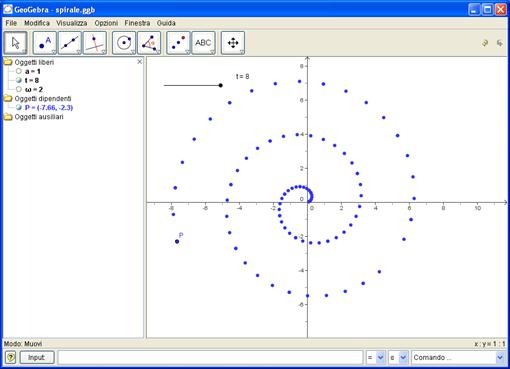
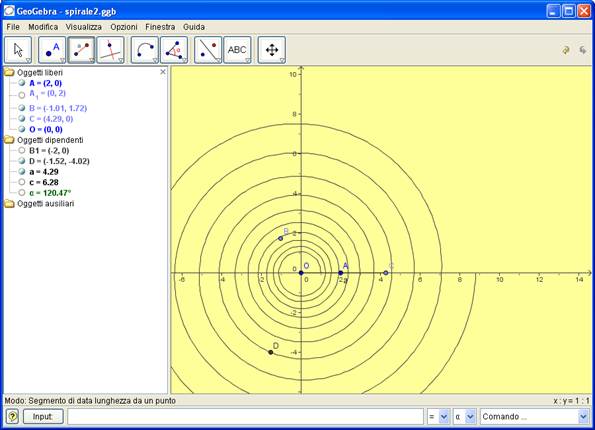
GRAFICO DELLA SPIRALE

Metodo analitico

Si definisce  il numero t come slider

Si definisce il punto P assegnandogli  le coordinate corrispondenti alle equazioni parametriche del luogo

Si assegna a P la proprietà <traccia on>>

Si fa variare t e si ottiene la <<traccia lasciata da P

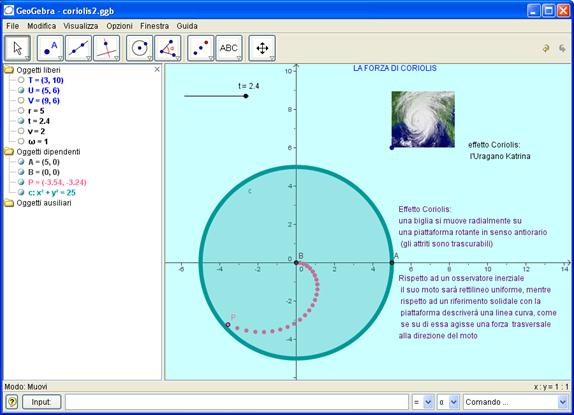
Nella figura è rappresentato anche il moto di un uragano, conseguenza della forza di Coriolis, ma in effetti non è un esempio di spirale di Archimede, bensì di spirale logaritmica

 

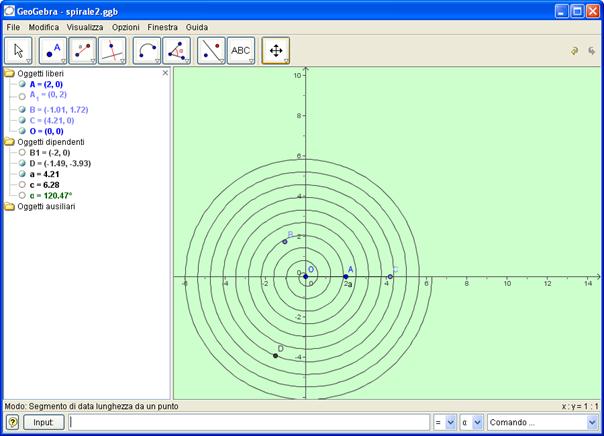
Metodo sintetico

Si sceglie il punto B su una semicirconferenza di centro O e diametro AB1 arbitrario

Si definisce l’angolo α formato dai raggi OA e OB e poi il punto C mediante lo strumento  <<segmento di data lunghezza>>: la lunghezza deve essere proporzionale ad α, per esempio 2 α

Si fa ruotare il punto C intorno  al punto O , mediante il comando ruota[D,20* α,O ] e si definisce  il punto D’

Si costruisce la spirale mediante il comando Luogo[D,B]

Si nascondono  gli altri oggetti ( tasto destro del mouse-mostra oggetto)

La spirale logaritmica

Si costruisce in modo analogo alla precedente, con la differenza che la distanza dall’origine cresce esponenzialmente rispetto all’angolo di rotazione.

La sua equazione , in coordinate polari, è ρ= a θ

Le equazioni parametriche  sono

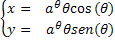
La spirale logaritmica ha suscitato l’interesse dei più noti matematici, da Cartesio a T, da Wallis a  JacKob Bernoulli .   Quest’ultimo  scoprí molte proprietà della curva  e ne rimase talmente affascinato che la scelse come epigrafe  sulla sua pietra tombale, accompagnata dalla scritta latina "Eadem mutata resurgo" (Sebbene cambiata, rinasco identica). Purtroppo ,per colpa  di uno  scalpellino poco esperto  , non solo la scritta non fu riportata, ma la spirale che ancora oggi è visibile sulla lapide del matematico a Basilea non è una spirale logaritmica, bensì una spirale di Archimede.

Metodo analitico

 

Una notevole proprietà della spirale logaritmica: Se gli angoli AOC e COE sono uguali, il segmento OC è medio proporzionale tra OA e OC .

Infatti , utilizzando l’equazione polare, e indicando con ρ1, ρ2, ρ3 le lunghezze de i tre segmenti   OA,OC,OE, potremo porre

ρ 2= a t         ρ1= at-α        ρ3= at+α  

da cui   (ρ 2) 2 = a 2t        

ρ1* ρ3= at-α +t+  α     = a 2t        

 

Metodo sintetico

Si procede come nel caso  della spirale di Archimede, con la differenza che il segmento OC deve avere lunghezza variabile  esponenzialmente  2α

Salta subito agli occhi  la  differenza tra i grafici delle due curve : i bracci successivi hanno una distanza fissa nella spirale di Archimede, mentre nella  spirale logaritmica le distanze seguono una progressione geometrica

C’è però una differenza ancora più interessante:

diversamente dalla spirale di Archimede, che ha un punto di inizio, la spirale logaritmica prosegue indefinitamente sia verso l'interno che verso l'esterno.

Infatti : nella spirale di Archimede la distanza ρ, del generico punto dall’origine, è nulla  in corrispondenza di α=0, invece  , per la proprietà della funzione esponenziale,  nella spirale logaritmica possiamo solo affermare che ρ tende a 0 quando α tende a -∞.

 Mano a mano che si avvicina al punto O, la curva ci si avvolge intorno infinite volte senza mai raggiungerlo!

 

Volendo percorrere  la spirale  dalla periferia al centro, possiamo costruire il luogo cambiando la definizione del punto Din modo che l’angolo assuma  valori negativi

Non c’è un limite al numero di giri  che si possono effettuare nell’intorno dell’origine , ma i limiti della rappresentazione grafica  non ne permettono la visualizzazione

 

 

 

 

 

 

LA CICLOIDE

Una circonferenza di raggio r rotola  senza strisciare su una retta t.

Qual è il luogo geometrico descritto da un punto P della circonferenza durante tale moto?

 

Ovviamente rispetto ad un riferimento (mobile) avente l’origine nel  centro della circonferenza e solidale con essa, la traiettoria coincide con la circonferenza stessa.

Consideriamo ora un riferimento (fisso) avente l’asse x coincidente con la retta  t e l’origine nel suo punto di contatto  con la circonferenza , punto che consideriamo come posizione iniziale di P

Sia P1 la posizione del punto dopo un tempo t, T il punto di contatto nello stesso istante, C il centro della circonferenza, 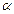 la misura dell’arco TP rettificato.

 

Sarà                                                                                             

          spostamento relativo                                                            

                                                                                                                               

Dalla relazione         

Essendo a sua volta                                                                   

      si ottiene   

                                                          

e, passando alle componenti lungo l’asse x e lungo l’asse y,

x = r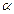t)

y = r –    r  cos, 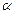t)

dove 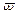 è la velocità angolare con cui P ruota sulla circonferenza.

Queste sono le equazioni parametriche del luogo geometrico richiesto, ma non è semplice risalire all’equazione cartesiana.

Geogebra ci fornisce il grafico, che può essere confrontato con un’analisi qualitativa

 

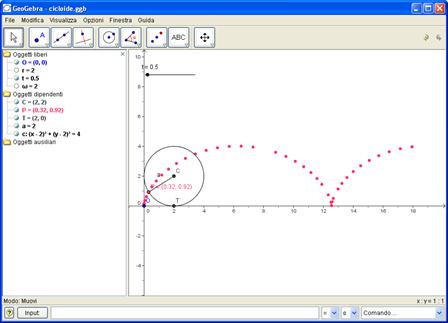
A) Risoluzione sintetica

Per simulare il rotolamento si costruisce una circonferenza il cui centro C dipende da un parametro t (slider numerico) e una retta b passante per C con coefficiente angolare anch’esso variabile in funzione di t.

Mentre C( 2t,r) trasla verso destra ,parallelamente all’asse  x , di un segmento vt, la retta b ruota in senso orario, di un angolo di ampiezza α= vt, rispetto alla direzione negativa dell’asse x (m= tan(π-vt)) Il punto B, intersezione di b con la circonferenza, descrive la Cicloide; il segmento CB ruota intorno a C.

 

 

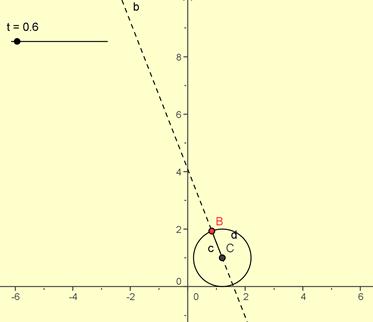
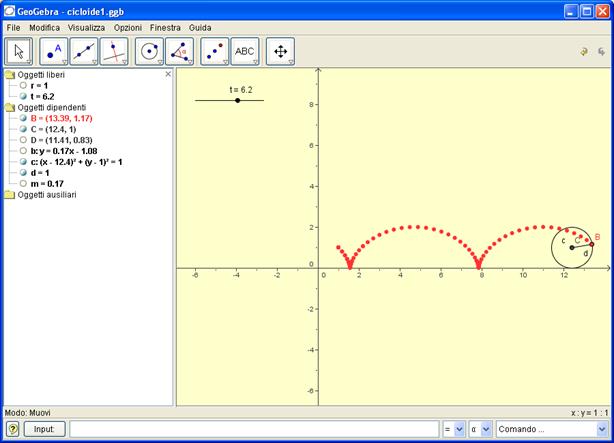
La curva ottenuta si chiama Cicloide (nome assegnatole da Galileo), ma è nota anche come la <<bella Elena>> della Matematica, non tanto per il suo profilo armonioso  quanto per le sfide, le controversie, i problemi e le dispute che  ha suscitato negli ambienti scientifici, grazie alle sue interessanti proprietà.

Meno  piacevoli sono gli aggettivi che definiscono  alcuni suoi aspetti, collegati con la Cinematica: tautocrona, isocrona, brachistocrona .Gli aggettivi derivano dal greco ed hanno senz’altro un suono più gradevole nella loro lingua di origine che non in italiano; quello che ci interessa è comunque il loro significato:

  Tautocrona (da tautos= stesso e chronos= tempo) indica la seguente proprietà: una massa posta su un  punto di un profilo a forma di un arco di cicloide rovesciata ( posto in posizione verticale) impiega lo stesso  tempo a  giungere nel punto più basso( punto di tautocronismo), qualunque sia la quota di partenza.

Isocrona : ( da isos= uguale  e chronos= tempo) è sostanzialmente sinonimo  dell’aggettivo precedente, ma in una diversa accezione: eventuali oscillazioni intorno al punto di tautocronismo  avvengono nello stesso tempo, indipendentemente dall’ampiezza

Brachistocrona:(da brachistos, minimo, e chronos, tempo) :rappresenta il percorso che fa impiegare il minor tempo per andare da un punto A a un punto B

Dal catalogo multimediale del Museo di Storia della Scienza di Firenze

“CICLOIDE:

È la curva generata da un punto della circonferenza di un cerchio che rotola su un piano. La cicloide presenta interessanti proprietà fisiche. Infatti, è brachistocrona e tautocrona: brachistocrona perché rappresenta il percorso superato nel tempo più breve tra due punti per un dato tipo di movimento (ad esempio la caduta per l'effetto della forza di gravità); tautocrona perché un grave posto in oscillazione lungo una cicloide la percorre sempre nello stesso tempo, qualunque sia l'ampiezza dell'oscillazione. Galileo (1564-1642) ritenne erroneamente tautocrone le oscillazioni circolari. La dimostrazione del brachistocronismo della cicloide fu fornita da Jacques Bernoulli (1654-1705) nel 1697, mentre Christiaan Huygens (1629-1695) ne dimostrò il tautocronismo nel 1659”

La Cicloide nel Laboratorio di Fisica

Apparecchio per dimostrare il tautocronismo

Lo strumento, proveniente dalle collezioni lorenesi, fu descritto da John Theophilus Desaguliers nel suo volume A Course of Experimental Philosophy (London, 1734) e da Willem Jacob 's Gravesande nei Physices elementa mathematica, experimentis confirmata (III ed., Leiden, 1742).

Su un lungo telaio di legno, munito alla base di tre viti calanti, sono realizzati due canali paralleli, che riproducono due cicloidi uguali terminanti entrambe in un canale rettilineo. Un filo a piombo (oggi mancante) consentiva di assicurare la perfetta verticalità dell'apparato, condizione essenziale per il buon esito dell'esperimento. L'esperimento consiste nel rilasciare contemporaneamente due biglie nei canali paralleli, ma da altezze diverse: le biglie arrivano sempre alla fine della cicloide simultaneamente. Viene in tal modo dimostrato sperimentalmente il tautocronismo della cicloide, una proprietà della cicloide dimostrata geometricamente da Christiaan Huygens, il quale nel 1659 concepì per primo un pendolo cicloidale, perfettamente tautocrono, che utilizzò come regolatore del movimento di un orologio.”

Brachistocronismo

 

.

“Questo apparecchio dimostra gli effetti osservabili di un principio fisico scoperto e comunicato a Guidobaldo del Monte da Galileo il 29 novembre 1602. Galileo dimostrò con metodi geometrici che un grave impiega minor tempo a discendere lungo l'arco di una circonferenza che non lungo la corda corrispondente (nonostante che quest'ultima sia più breve). Galileo, che considerava l'arco come equivalente a un insieme infinito di piani inclinati, non si rese conto che il percorso brachistocrono di un grave che scende tra due punti è l'arco di cicloide, e non l'arco di cerchio. La dimostrazione matematica del brachistocronismo della cicloide sarà fornita da Jacques Bernoulli nel 1697.

L'apparecchio si compone di un telaio di legno recante un canale cicloidale. Sul telaio è imperniato anche un canale rettilineo, la cui inclinazione può essere fissata mediante pioli infissi in appositi fori muniti di ghiere di ottone praticati sotto la cicloide. Lasciando cadere simultaneamente due sferette lungo i due canali, si osserva che la sferetta lungo l'arco di cicloide anticipa nettamente quella lungo il piano inclinato”

 

CONCLUSIONE

Lo studio dei luoghi geometrici  ha fornito molti spunti che vanno al di  là dei calcoli e delle costruzioni grafiche, rivelando vari aspetti pluridisciplinari.

ORA TOCCA A TE:

WEBQUEST!

Fai una ricerca su alcune curve celebri e prova a costruirne il grafico con GEOGEBRA.

Puoi anche approfondire lo studio delle curve già analizzate  in questo articolo o trovarne altri metodi di costruzione.

I lavori meritevoli saranno pubblicati nel Blog.

Buon lavoro!

Letture consigliate": Autore: Luciano Cresci
Titolo: Le curve celebri
Editore: Franco Muzzio Editore

Siti consigliati
http://www.xahlee.org/PageTwo_dir/more.html

http://www.fmboschetto.it/images/galleria_matematica.htm

 

Fonte: http://alabis.files.wordpress.com/2009/05/digressione-sui-luoghi-geometrici.doc

Autore del testo: non indicato nel documento di origine

Parola chiave google : luoghi geometrici tipo file : doc

 

 

 

 

Visita la nostra pagina principale

 

luoghi geometrici

 

Termini d' uso e privacy

 

 

 

 

luoghi geometrici