Matematica matrici
Matematica matrici
I riassunti, le citazioni e i testi contenuti in questa pagina sono utilizzati per sole finalità illustrative didattiche e scientifiche e vengono forniti gratuitamente agli utenti.
MATRICI
Cenni storici
Gli inizi delle matrici e dei determinanti risalgono al secondo secolo a.C., sebbene alcune tracce fanno pensare addirittura a periodi risalenti al quarto secolo a.C. Comunque non prima del diciassettesimo secolo questi argomenti riapparvero e si svilupparono.
I primi approcci con matrici e determinanti furono inerenti allo studio di sistemi di equazioni lineari. I babilonesi ad esempio studiarono problemi con più equazioni lineari, di questi è infatti rimasta traccia in alcune tavole ritrovate.
Per esempio una tavola risalente al 300 a.C. conteneva un problema del genere:
Ci sono due campi, la cui area totale è di 1800 yards quadrate. Uno produce grano per 2/3 di bushel per yard quadrata mentre l'altro 1/2. Se il rendimento totale è di 1100 bushels, qual'è la dimensione di ciascun campo ?
Introduzione
Un modo molto comune di rappresentare e organizzare dati o informazioni è quello di ricorrere a delle tabulazioni.
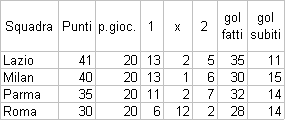
Si pensi ad esempio alla tabella riportante la classifica di un campionato di calcio riferita alle prime 4 squadre in classifica, si ha:
oppure l'orario delle lezioni relativo al primo anno di una facoltà di Economia
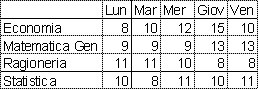
Quando le informazioni raccolte sono rappresentate da numeri si parla di matrici.
Definizione di matrice
Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne.
I numeri che compaiono nella tabella si dicono elementi della matrice .
La loro individuazione avviene attraverso la loro posizione di riga e colonna.
Il primo indice è l'indice di riga mentre il secondo è l'indice di colonna.
Ad esempio, il quadro di numeri
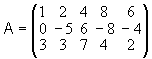
disposto su 3 righe e 5 colonne è una matrice 3 x 5.
L'elemento 8 essendo posizionato sulla prima riga e quarta colonna è indicato con ![]() .
.
In generale gli elementi di una matrice A si indicano con il simbolo ![]() dove il primo indice i indica la riga di appartenenza mentre il secondo indice j precisa la colonna a cui l'elemento appartiene, così ad esempio si ha
dove il primo indice i indica la riga di appartenenza mentre il secondo indice j precisa la colonna a cui l'elemento appartiene, così ad esempio si ha
![]() = elemento che compare nella seconda riga e quinta colonna = -4
= elemento che compare nella seconda riga e quinta colonna = -4
In generale una matrice A di m righe e n colonne si denota con
A = 
oppure in forma più sintetica A = ( ![]() ) i = 1 .. m , j = 1 .. n
) i = 1 .. m , j = 1 .. n
In generale le matrici sono denotate con lettere maiuscole dell'alfabeto mentre i loro elementi con la corrispondente lettera minuscola abbinata al doppio indice.
Il numero di righe e di colonne di una matrice è detto ordine o dimensione della matrice.
L'importanza delle matrici va al di là del fatto che tramite esse è possibile organizzare in modo semplice dei dati; vengono impiegate ad esempio, oltre che in matematica, nella statistica per lo studio della varianza e covarianza e nell'economia per lo studio dei modelli lineari di produzione.

Uguaglianza tra matrici
Due matrici A e B si dicono uguali se hanno la stessa dimensione e se ![]() per ogni i , j
per ogni i , j
Esempio
Si considerino le seguenti matrici
A = 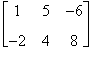
Si osservi che ![]()
Sottomatrice
Una sottomatrice di una matrice A è la matrice che si ottiene cancellando da A righe e / o colonne.
Esempio
Si consideri la matrice
A = 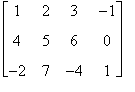
La matrice A'= 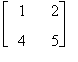 è ottenuta eliminando la terza riga e la terza e quarta colonna di A e pertanto è una sottomatrice di A.
è ottenuta eliminando la terza riga e la terza e quarta colonna di A e pertanto è una sottomatrice di A.
A''= ![]() è anch'essa una sottomatrice di A in quanto da essa ottenuta eliminando la prima e terza riga, e la prima e la quarta colonna.
è anch'essa una sottomatrice di A in quanto da essa ottenuta eliminando la prima e terza riga, e la prima e la quarta colonna.
La matrice 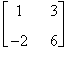 non è invece una sottomatrice di A in quanto non è da essa ottenibile tramite cancellazione di righe e/o colonne.
non è invece una sottomatrice di A in quanto non è da essa ottenibile tramite cancellazione di righe e/o colonne.
Matrice Trasposta
Si dice trasposta di una matrice A e si indica con il simbolo AT , la matrice ottenuta da A scambiando ordinatamente le righe con le colonne.
Esempio
Data la matrice
A = 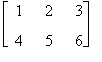
Evidentemente se A è m x n allora AT è di ordine n x m.
Escluso il caso in cui sia A matrice quadrata, la trasposta di A è sicuramente diversa da A avendo le due matrici diverse dimensioni.
Anche nel caso di matrici in cui m = n la trasposta, salvo rare eccezioni, è diversa dalla matrice data.
Esempio
Rispetto alla matrice quadrata
A = 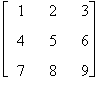
la sua trasposta è
AT = 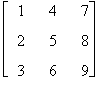
Si osservi che A¹AT
Vettori riga e vettori colonna
Una matrice costituita da una sola riga è detta vettore riga .
Ad esempio
![]() è un vettore riga
è un vettore riga
Una matrice costituita da una sola colonna è detta vettore colonna .
Ad esempio
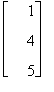 è un vettore colonna
è un vettore colonna
Ovviamente il trasposto di un vettore riga è un vettore colonna e viceversa.
Matrice quadrata
Una matrice è detta quadrata se il numero delle righe è uguale al numero delle colonne.
In questo caso il numero delle righe (colonne) è detto ordine della matrice.
A = 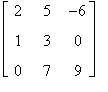
Matrice quadrata di ordine 3
Diagonale principale
Data una matrice quadrata di ordine n, si definisce diagonale principale di A l'insieme degli elementi di uguale indice ovvero:
![]()
Esempio
Rispetto alla matrice
A = 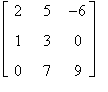
la diagonale principale è costituita dagli elementi: 2 , 3 , 9
Matrice Identica
Una matrice quadrata avente gli elementi della diagonale principale uguali a 1 e i restanti uguali a zero è detta matrice identica .
Indicheremo la matrice identica con I o con In se ne dobbiamo precisare l'ordine.
Esempio
I2= 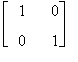
I3 = 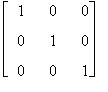
Matrice simmetrica
Sia A quadrata di ordine n. A è detta simmetrica se ![]() .
.
Osserviamo che A è simmetrica se e solo se A=AT .
Esempio
Si considerino le matrici
A = 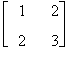
Risulta A = AT ,B¹BT ovvero A è una matrice simmetrica mentre B non lo è.
Matrice triangolare inferiore (superiore)
Una matrice triangolare inferiore ( superiore ) è una matrice quadrata i cui elementi al di sopra (sotto) della diagonale principale sono tutti nulli.
Matrice triangolare superiore 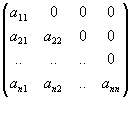
Matrice triangolare inferiore 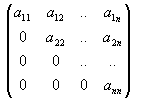
Matrice diagonale
Una matrice è detta diagonale se ![]()
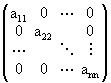
Si osservi che una matrice diagonale è simmetrica, ed è sia triangolare superiore che inferiore
Esercizio:
Si consideri la matrice A = 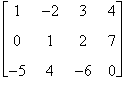
a) Determinare la sottomatrice di A ottenuta cancellando la prima e terza riga e la seconda colonna.
b) Detrminare la trasposta di A
Operazioni tra matrici
Somma tra matrici
Siano A=(aij ) e B=(bij ) due matrici aventi la stessa dimensione m x n.
Si definisce somma delle matrici A e B, la matrice C = A + B il cui generico elemento è dato da
![]()
Si tratta in pratica di sommare tra loro gli elementi di ugual posizione di riga e colonna.
Ovviamente se A e B sono m x n anche C è m x n.
Esempio
Si considerino le matrici
A = 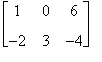
Risulta
C = A + B = 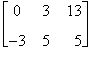
così ottenuta:
c11=a11+b11= 1 + (-1) = 0
c12=a12+b12 = 0 + 3 = 3
c13=a13+b13= 6 + 7 = 13
c21=a21+b21= -2 + (-1) = -3
c22=a22+b22= 3 + 2 = 5
c23=a23+b23= (-4) + 9 = 5
Proprietà della somma
Poichè la somma tra matrici si esegue sommando gli elementi di ugual posizione che sono numeri reali, è facile verificare che essa soddisfa le seguenti proprietà:
Proprietà Associativa
Siano A , B , C matrici di dimensione m x n risulta
A + ( B + C ) = ( A + B ) + C
Esempio
Verifichiamo la proprietà associativa rispetto alle seguenti matrici
A = 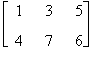
Risulta
A + ( B + C ) = 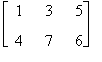
( A + B ) + C = 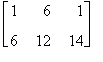
da cui A + (B + C)=(A + B) + C
Proprietà Commutativa
Siano A e B matrici m x n risulta
A + B = B + A
Esempio
Verifichiamo la proprietà commutativa rispetto alle matrici
A = 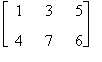
Risulta
A + B = 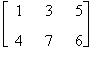
B + A = 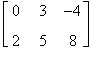
da cui A + B = B + A
Esistenza dell'elemento neutro rispetto alla somma
Sia A una matrice m x n, esiste una matrice 0 di dimensione m x n avente tutti gli elementi uguali a zero, detta matrice nulla , tale che
A + 0 = A
la matrice nulla 0 è detta elemento neutro rispetto alla somma.
Esempio
Si consideri la matrice
A = 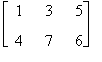 e la matrice nulla di egual dimensione
e la matrice nulla di egual dimensione
risulta
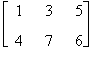
Esistenza dell'opposto
Per ogni matrice A m x n esiste una matrice denotata con -A, tale che A + (-A) = 0
-A è detta matrice opposta di A e si ottiene da A cambiando ordinatamente di segno i suoi elementi
-A = (-ai,j ) "i,"j
Esempio
Si consideri la matrice
A = 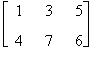
la matrice opposta di A è data da
-A = 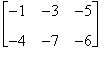
risulta
A + (-A) = 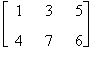

Prodotto di una matrice per uno scalare
Dato un numero reale k (detto scalare) ed una matrice A = ( ai,j ), si definisce prodotto della matrice A per lo scalare k la matrice indicata con k A il cui generico elemento è k ai,j
Esempio
Si consideri la matrice
A = 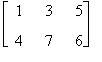 e lo scalare k = 3
e lo scalare k = 3
k A = 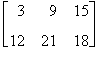
Osserviamo che (-1) A = -A, ovvero il prodotto tra lo scalare -1 e la matrice A dà come risultato l'opposta di A.
Proprietà del prodotto per uno scalare
Anche nel caso del prodotto per uno scalare è immediato verificare le seguenti proprietà
Per ogni matrice A,B di dimensione m x n e per ogni k,h numeri reali risulta
1) ( k + h ) A = k A + h A
2) k ( A + B ) = k A + k B
3) ( k h ) A = k ( h A)
4) 1 A = A
Osservazione
- Essendo i vettori particolari matrici valgono per essi le stesse operazioni con le relative proprietà
- L'insieme delle matrici m x n dotato delle 2 operazioni di somma e prodotto per uno scalare con le relative proprietà è uno spazio vettoriale
![]()
Prodotto tra matrici
Sia A una matrice m x n e B una matrice n x k, si definisce prodotto tra le matrici A e B la matrice C = A B il cui generico elemento ci,j è la somma dei prodotti degli elementi della i-esima riga di A per i corrispondenti elementi della j-esima colonna di B, ovvero
![]()
il prodotto tra la i-esima riga di A e la j-esima colonna di B così definito è detto prodotto scalare .
La matrice prodotto C ha tante righe quante sono le righe di A e tante colonne quante sono le colonne di B.
Osservazione
Per verificare la possibilità di poter moltiplicare la matrice A di ordine p x q con la matrice B di ordine r x s conviene scrivere
(p x q)(r x s)
Si hanno così quattro numeri: 2 esterni (p ed s) e 2 interni (q e r). E' possibile effettuare il prodotto A B se e solo se gli interni coincidono cioè q = r.
In tal caso la matrice C = A B ha per ordine quello individuato dai due numeri esterni presi nell'ordine, cioè p x s.
Il prodotto tra matrici è anche detto prodotto riga colonna .
Esempio
Si considerino le matrici
A = 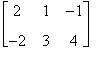
Poichè A ha dimensione (2 x 3) e B (3 x 4) è possibile eseguire il prodotto tra queste due matrici e la dimensione di C = A B è (2 x 4).
Vediamo come si determina tale matrice.
L'elemento di posto c11 è dato dal prodotto scalare tra la prima riga di A e la prima colonna di B ovvero:
![]() = (2·1+1·2+(-1)·(-1)) = 5
= (2·1+1·2+(-1)·(-1)) = 5
--------
c12= (I riga di A)x(II colonna di B) =
![]() = (2·1+1·(-3)+(-1)·(-1)) = 0
= (2·1+1·(-3)+(-1)·(-1)) = 0
--------
c13 = (I riga di A)x(III colonna di B) =
![]() = (2·2+1·1+(-1)·5)) = 0
= (2·2+1·1+(-1)·5)) = 0
---------
c14 = (I riga di A)x(IV colonna di B) =
![]() = (2·2+1·3+(-1)·2) = 5
= (2·2+1·3+(-1)·2) = 5
---------
c21 = (II riga di A)x(I colonna di B) =
![]() = ((-2)·1+3·2+4·(-1)) = 0
= ((-2)·1+3·2+4·(-1)) = 0
----------
c22 = (II riga di A)x(II colonna di B) =
![]() = ((-2)·1+3·(-3)+4·(-1)) = -15
= ((-2)·1+3·(-3)+4·(-1)) = -15
----------
c23 = (II riga di A)x(III colonna di B) =
![]() = ((-2)·2+3·1+4·5)) = 19
= ((-2)·2+3·1+4·5)) = 19
----------
c24 = (II riga di A)x(IV colonna di B) =
![]() = ((-2)·2+3·3+4·2) = 13
= ((-2)·2+3·3+4·2) = 13
Ovvero
C = A B = 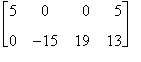
Osservazione
Con riferimento alle matrici A e B dell'esempio precedente non è possibile effettuare il prodotto B A in quanto considerando le dimensioni (3 x 4) (2 x 3) gli interni non coincidono.
E' possibile effettuare sia il prodotto A B che il prodotto B A quando in (p x q) (r x s) coincidono sia gli elementi interni che gli elementi esterni. Risulta però in generale AB¹BA.
Da ricordare:
Il prodotto tra matrici NON E' SEMPRE eseguibile
Se è possibile eseguire il prodotto A B non è detto che si possa eseguire il prodotto B A e quindi bisogna stare attenti all'ordine in cui si deve eseguire la moltiplicazione.
Se due matrici sono quadrate e dello stesso ordine si può eseguire sia il prodotto A B che il prodotto B A ottenendo una matrice quadrata dello stesso ordine, anche in questo caso però il prodotto non è in generale commutativo.
Come mostra il seguente esempio:
si considerino le matrici
A = 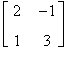
Risulta
AB = 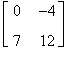
BA = 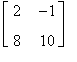
e quindi AB¹BA.
Proprietà del prodotto tra matrici quadrate
Si consideri l'insieme delle matrici quadrate di ordine n, valgono le seguenti proprietà:
Proprietà associativa
A ( B C ) = (A B ) C " A , B , C
Esistenza dell'elemento neutro rispetto al prodotto
La matrice identica I di ordine n è l'elemento neutro rispetto al prodotto.
Risulta infatti
A I = I A = A " A
Proprietà distributiva
A ( B + C ) = A B + A C " A , B , C
Inversa di una matrice
Come è noto, nell'insieme dei numeri reali si definisce l'inverso o reciproco di un numero a, quel numero che moltiplicato per a dà come risultato 1 ovvero l'elemento neutro rispetto al prodotto.
In modo del tutto analogo si può definire l' inversa di una matrice quadrata.
Sia A una matrice quadrata di ordine n.
Si definisce matrice inversa di A o più semplicemente inversa di A e si indica con il simbolo A-1 la matrice quadrata (se esiste) di ordine n tale che
A A-1 = A-1 A = I
Se una matrice A ha inversa allora A è detta invertibile o non singolare
Mentre per un numero reale esiste una semplice regola per verificare l'esistenza del suo inverso e per determinarlo ( a ha inverso ![]() ; l'inverso di a è 1/a), non è altrettanto facile stabilire l'invertibilità di una matrice.
; l'inverso di a è 1/a), non è altrettanto facile stabilire l'invertibilità di una matrice.
A tale riguardo la definizione di inversa non fornisce nessun elemento utile, se non per casi particolari quali ad esempio i seguenti:
- Se una matrice ha una riga di zeri (ad esempio la prima riga), il prodotto tra tale matrice ed una qualsiasi altra dello stesso ordine produrrà sempre la prima riga tutta nulla di conseguenza una tale matrice non è invertibile in quanto la definizione di inversa richiede che in ogni riga ci sia un elemento uguale ad 1.
Esempio
Si consideri la matrice A = 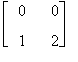 .
.
Risulta AB = 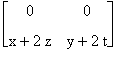 e quindi A non è invertibile.
e quindi A non è invertibile.
- Se una matrice è diagonale allora è invertibile se e solo se gli elementi ![]() .
.
Esempio
Si consideri la matrice diagonale
D = 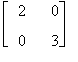
risulta
![]()
Infatti
![]()
Si osservi inoltre che anche se una matrice ha elementi tutti diversi da zero non è detto che sia invertibile come mostra il seguente
Esempio
Sia
A = 
Verifichiamo utilizzando la definizione che la matrice A non è invertibile, ovvero che non esiste una matrice B tale che A B = B A = I. Denotiamo con B = 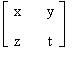 la matrice cercata.
la matrice cercata.
Risulta
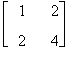
se e solo se x , y , z , t verificano i seguenti sistemi:
![]()
Poichè il primo membro della seconda equazione è il doppio della prima, il sistema risulta impossibile e quindi A non ammette inversa.
Per comprendere come si arriva a determinare condizioni di invertibilità, si consideri una matrice generica di dimensioni 2 x 2
A = 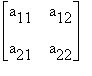
E' possibile dimostrare che:
Teorema
La matrice A è invertibile se e solo se a11a22- a21a12 ¹ 0,
In tal caso la matrice inversa di A è
![]()
Uno sguardo alla matrice ottenuta fa comprendere una semplice regola di calcolo: per trovare l'inversa di A (2 x 2) basta scambiare tra loro gli elementi sulla diagonale principale, cambiare di segno gli altri elementi e dividere tutto per il numero
a11a22- a21a12 chiamato determinante di A.
![]()
Determinante di una matrice di ordine n
In generale ad ogni matrice quadrata è possibile associare un numero reale detto determinante, indicato in generale con il simbolo |A| oppure det A, che permette di stabilire l'invertibilità o meno di una matrice.
Il calcolo di questo numero è effettuato tramite il cosiddetto sviluppo di Laplace che può essere eseguito rispetto ad una qualsiasi riga oppure rispetto ad una qualsiasi colonna.
Sviluppo di Laplace (rispetto alla riga i-esima)
La formula dello sviluppo di Laplace rispetto alla riga i-ma di una matrice A di ordine n è la seguente:
|A| = 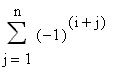 aijdet Aij
aijdet Aij
dove Aij è la sottomatrice ottenuta da A cancellando la i-ma riga e la j-ma colonna.
Il determinante det Aij è detto minore complementare dell'elemento aij ;
il prodotto (-1)i+jdet Aij è detto complemento algebrico .
In base a tale nomenclatura possiamo dire che:
Primo teorema di Laplace: il determinante di una matrice quadrata A è pari alla somma dei prodotti degli elementi di una riga qualsiasi per i rispettivi complementi algebrici.
Esempio
Si consideri la matrice
A = 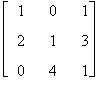
Calcoliamo il determinante sviluppando rispetto alla prima riga, ovvero
det A = (-1)1+11·det A11+ (-1)1+20 ·det A12 + (-1)1+31·det A13
da cui
det A = det 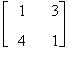
ovvero il calcolo del determinante di A è ricondotto al calcolo di 3 determinanti 2 x 2.
Si ottiene così
det A = (1)(1)(1·1 - 4·3) + (-1)(0)(2·1 - 0·3) + (1)(1)(2·4 - 0·1) = 1 -12 + 0 + 8 = -3
Verifichiamo che applicando lo sviluppo di Laplace rispetto ad un'altra riga ad esempio la terza, si ottiene lo stesso numero.
Si ha
det (A) = (-1)3+10·det A31+ (-1)3+2 4 ·det A32 + (-1)3+31·det A33 =
= -4 det 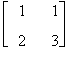 = - 4 + 1 = - 3
= - 4 + 1 = - 3
Sviluppo di Laplace rispetto ad una colonna
Si può dimostrare che lo sviluppo di Laplace rispetto ad una qualsiasi colonna individua sempre il determinante ovvero:
|A| = 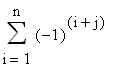 aijdet Aij
aijdet Aij
Si ha così:
Secondo teorema di Laplace: il determinante di una matrice (quadrata) A è pari alla somma dei prodotti degli elementi di una colonna qualsiasi per i rispettivi complementi algebrici.
Osservazione
Il calcolo del determinante di una matrice di dimensione 4 x 4 , sviluppando ad esempio rispetto alla prima riga, è pari a:
det A= a11 det A11 - a12 det A12 + a13 det A13 - a14 detA14
dove adesso le sottomatrici A11 , A12 , A13 ,A14 sono di dimensioni 3 x 3 quindi per completare il calcolo dobbiamo riapplicare lo sviluppo di Laplace a tali sottomatrici.
Ovviamente nel selezionare una riga o una colonna per applicare lo sviluppo di Laplace si sceglierà quella che contiene il maggior numero di zeri allo scopo di ridurre al minimo i calcoli necessari.
In ogni caso per matrici di grandi dimensioni il numero dei calcoli diviene enorme e il tempo richiesto per eseguirli può diventare lungo anche per un elaboratore elettronico.
Come vedremo, però il determinante gode di diverse proprietà alcune delle quali particolarmente utili per il calcolo del determinante stesso.
Considerazioni sullo sviluppo di Laplace
Riassumendo se ad esempio A è di dimensione 5 x 5 si devono calcolare (in generale) 5 determinanti di matrici di dimensioni 4 x 4. Il calcolo di tali determinanti comporta il calcolo di 4 determinanti di matrici di dimensioni 3 x 3, ovvero 20 determinanti di matrici di dimensioni 3 x 3.
A sua volta ogni calcolo di un determinante di una matrice di dimensione 3 x 3 comporta il calcolo dei determinanti di 3 matrici di dimensione 2 x 2 .
Quindi per calcolare il determinante di una matrice di dimensione 5 x 5 si devono calcolare 60 (5•4•3) determinanti di matrici di dimensioni 2 x 2.
Regola di Sarrus
Nel caso di una matrice quadrata di ordine 3, è possibile calcolare il determinante con la regola di Sarrus:
si accostano alla terza colonna della matrice la prima e la seconda colonna, ovvero:
Quindi si esegue la somma dei prodotti degli elementi situati sulle diagonali di colore blu e si sottrae la somma dei prodotti degli elementi situati sulle diagonali di colore rosso, ovvero
det A = ![]() +
+
- ![]()
la regola di Sarrus è valida solo per matrici di dimensioni 3 x 3 !
Esempio
Calcolare con la regola di Sarrus il determinante della matrice
A = 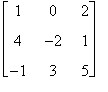
si ha quindi
det A = -10 + 0 + 24 - 4 - 3 - 0 = 7
Proprietà del determinante
Sia A una matrice quadrata di ordine n
Proprietà 1
Se ![]()
Proprietà 2
Sia A = ( ![]() .
.
Risulta ![]()
Una analoga proprietà vale per le righe di una matrice.
Proprietà 3
Se A ha due colonne (righe) uguali allora det A = 0
Proprietà 4
Il determinante della matrice identica di ordine n è uno ovvero det I = 1
Le proprietà 1 , 2 , 3 , 4 permettono di determinare altre importanti proprietà, alcune delle quali sono sotto riportate, e di stabilire l'unicità del determinante. Si può verificare che lo sviluppo di Laplace rispetto ad una qualsiasi riga o colonna fornisce un numero che verifica le proprietà 1 , 2 , 3 , 4 , quindi tale numero per l'unicità, è necessariamente il determinante.
Si giustifica così il fatto che il calcolo di un determinante è indipendente dalla scelta della riga o della colonna nello sviluppo di Laplace.
Proprietà 5
Se una colonna (riga) di A è formata da elementi nulli allora det A = 0.
Proprietà 6
Se ![]() .
.
Proprieta 7
Se si addiziona ad una colonna (riga) un multiplo scalare di un'altra, il valore del determinante non cambia.
Proprietà 8
det AT = det A
Le proprietà 1 - 2 - 3 - 4 garantiscono l'unicità del determinante.
Casi particolari
Se A è una matrice diagonale o triangolare superiore o triangolare inferiore allora il determinante di A è dato dal prodotto degli elementi sulla diagonale principale, ovvero:
det A = a11a22 a33...ann
Teorema di Binet
Vediamo adesso come si comporta il determinante rispetto alle operazioni di somma e prodotto tra matrici quadrate.
Mentre non vi è nessuna relazione che lega il determinante di una somma di due matrici con i determinanti delle singole matrici, per il prodotto si ha il seguente teorema.
Teorema di Binet
Siano A e B matrici di qualsiasi ordine. Allora det AB = det A·det B

Esistenza e proprietà dell'inversa di una matrice
Vediamo adesso come l'introduzione del determinante permette di caratterizzare l'invertibilità di una matrice. Vale il seguente teorema
Teorema
Sia A una matrice quadrata di ordine n,
A è invertibile se e solo se detA¹ 0 .
Inoltre se detA¹ 0 allora gli elementi cij di A-1 sono dati da
![]()
dove la matrice Aji è la matrice ottenuta da A cancellando la j-ma riga e la i-ma colonna
Osservazione
Il precedente teorema permette di ritrovare le regole di calcolo relative alla determinazione dell'inversa di una matrice 2 x 2 e di una matrice diagonale
Proprietà della matrice inversa
Sia A una matrice quadrata di ordine n
Proprietà 1
Se esiste l'inversa di A essa è unica
![]()
Proprietà 2
Se esiste una matrice B tale che A B = I (oppure B A = I) allora B è l'inversa di A ovvero
![]() .
.
![]()
Proprietà 3
Se A è invertibile di ordine n, allora l'inversa di A-1 coincide con A ovvero
![]() .
.
![]()
Proprietà 4
Siano A e B due matrici invertibili di ordine n, risulta allora che
![]()
![]()
Caratteristica di una matrice
Come abbiamo visto il determinante è un numero reale che è associato ad ogni matrice quadrata. Quindi se abbiamo una matrice non quadrata non ha significato calcolarne il determinante.
Però una qualsiasi matrice possiede sottomatrici quadrate. Ad esempio una matrice 3 x 5 possiede sottomatrici quadrate di ordine 1 , 2 , 3 e per tali sottomatrici è possibile calcolare il determinante. Sarà importante, soprattutto per la risolubilità dei sistemi lineari che tratteremo successivamente, determinare la dimensione massima delle sottomatrici quadrate per le quali almeno una ha determinante diverso da zero. Tale dimensione è detta caratteristica .
Da un punto di vista formale si ha la seguente definizione:
La caratteristica o rango di una matrice A, denotata con il simbolo r(A), è il massimo ordine dei minori non nulli.
Con minore si intende il determinante di una sottomatrice quadrata e con ordine la dimensione di tale sottomatrice.
Ad esempio dire che r(A) = 5 significa che esiste almeno una sottomatrice quadrata di ordine 5 con determinante diverso da zero e tutte le sottomatrici di ordine superiore (se esistono) hanno determinante uguale a zero.
Esempio
Determinare la caratteristica della matrice
A = 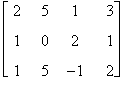
Essendo A di dimensioni 3 x 4, la massima dimensione di una sua sottomatrice quadrata è 3 e quindi r(A)£3 .
In generale se A è del tipo m x n r(A)£min{m,n}
Poichè la matrice A possiede almeno un elemento diverso da zero, la sua caratteristica è sicuramente maggiore uguale a 1, in particolare in questo caso avremo
![]()
Per stabilire se r(A) = 3 si devono calcolare i determinanti delle sottomatrici 3 x 3 che sono le seguenti:
![]()
![]()
Calcoliamo i determinanti con la regola di Sarrus
det A1 = det 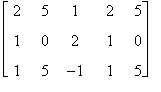 = 0 + 10 + 5 - 0 - 20 + 5 = 0
= 0 + 10 + 5 - 0 - 20 + 5 = 0
det A2 = det 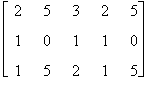 = 5 + 15 - 10 - 10 = 0
= 5 + 15 - 10 - 10 = 0
det A3= det A4 = 0
Poichè tutte le sottomatrici di dimensioni 3 x 3 hanno determinante uguale a zero si ha
![]() .
.
Si passa ad analizzare le sottomatrici di dimensioni 2 x 2 fino a che se ne trova, se esiste, una con determinante diverso da zero. Poichè ad esempio
det 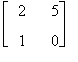 = - 5 ¹ 0 si ha r(A) = 2
= - 5 ¹ 0 si ha r(A) = 2
Regola di Kronecker
Tale regola permette di ridurre il numero dei determinanti da calcolare ai fini della individuazione della caratteristica.
Vale il seguente
Teorema
Una matrice A ha caratteristica p se e solo se esiste almeno una sottomatrice di ordine p con determinante diverso da zero e ogni sottomatrice di ordine p+1 che la contiene ha determinante uguale a zero.
Rispetto all'esempio precedente si consideri l'elemento di posto (1,1) come matrice 1 x 1. Poichè tale elemento è diverso da zero ci poniamo il problema se tutte le matrici 2 x 2 che lo contengono hanno determinante uguale a zero.
Poichè la sottomatrice 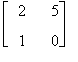 ha determinante diverso da zero, r(A) > 1 ovvero r(A)³ 2.
ha determinante diverso da zero, r(A) > 1 ovvero r(A)³ 2.
Ci domandiamo se è r(A) = 2. Al riguardo basta analizzare solo le sottomatrici 3 x 3 che contengono 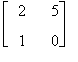 , cioè A1 e A2 ; avendo quest'ultime determinante uguale a zero si deduce che
, cioè A1 e A2 ; avendo quest'ultime determinante uguale a zero si deduce che
r(A) = 2
Osservazione
Si osservi che utilizzando questa regola si è calcolato solo due determinanti di sottomatrici di dimensione 3 x 3 invece dei 4 calcolati in precedenza

Forma canonica di Jordan
Abbiamo già rilevato che la determinazione della caratteristica di una matrice tramite la definizione comporta calcoli onerosi.
Nasce quindi il problema di individuare procedimenti che permettano uno snellimento di tali calcoli.
Iniziamo ad osservare che esistono particolari matrici per le quali la determinazione della caratteristica è immediata, non richiedendo alcun calcolo.
Si consideri ad esempio la matrice
A = 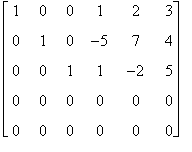
La caratteristica di A è 3 in quanto:
- esiste una sottomatrice 3x3 con determinante diverso da zero: la sottomatrice identica I3 che compare nelle prime tre righe e colonne.
- ogni matrice quadrata contenente I3 ha necessariamente una riga nulla e quindi ha determinante uguale a zero.
Ne consegue che la caratteristica non può aumentare e quindi r(A) = 3.
In generale una matrice come quella dell'esempio ha una struttura del tipo
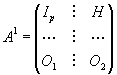
dove Ip è la matrice identica di ordine p, H è una matrice di dimensionie p x (n - p) e O1 e O2 sono due matrici nulle, rispettivamente di dimensione (m-p) x p, e di dimensione (m-p) x (n-p).
Ripetendo il ragionamento precedente si conclude immediatamente che r(A) = p.
L'idea alla base del calcolo della caratteristica di una matrice con il metodo di Jordan è quella di ridurla ad una forma del tipo A1 che è detta forma canonica di Jordan .
Ciò può essere fatto tramite le così dette operaazioni riga elementari:
Operazioni riga elementari
Consistono in:
Scambio di due righe
Moltiplicazione di una riga per uno scalare non nullo
Sostituzione di una riga con la somma di se stessa e di un'altra moltiplicata per uno scalare.
Matrici ottenibili l'una dall'altra con operazioni riga elementari sono dette
equivalenti per riga.
Teorema
La caratteristica di una matrice è invariante per operazioni riga elementari. Ovvero:
se B è una matrice ottenuta da una matrice A operando con operazioni riga elementari , allora
r(A) = r(B)
![]()
Come ottenere la forma canonica
Per determinare la forma canonica di una matrice si effettua una sequenza finita di operazioni riga elementari.
Per trasformare la colonna j-ma di una matrice in una colonna della matrice identica con elemento 1 in posizione ij si effettuano le seguenti operazioni riga elementari che prendono il nome di operazione di cardine :
- sostituzione della k-ma riga (k ¹ i) con
![]()
- sostituzione della i-ma riga con
![]()
L'elemento aij¹ 0 prende il nome di cardine o pivot .
Si osservi che le operazioni indicate possono portare ad avere la matrice identica Ip non necessariamente nelle prime p righe e colonne.
Possibili forme canoniche
- A matrice di dimensione m x n con m < n
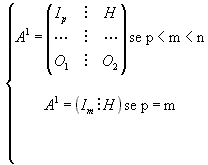
- A matrice di dimensione m x n con m > n
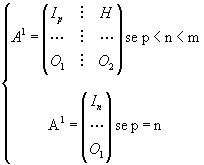
- A matrice di dimensione m x n con m = n
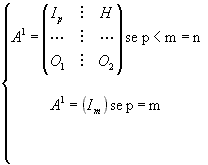
In quest'ultimo caso r(A) = m = n significa anche che il determinante di A è diverso da zero ovvero che A è invertibile.
Calcolo della matrice inversa con il metodo di Jordan
Le operazioni di cardine ovvero la riduzione di A nella sua forma canonica permettono di ottenere, quando il determinate di A è diverso da zero, l'inversa della matrice A.
Più precisamente si considera una matrice di dimensioni n x 2n ottenuta affiancando ad A la matrice identica di ugual dimensione
![]()
Si può dimostrare che le operazioni elementari che trasformano A in I trasformano I in A-1 ovvero
![]()
Esempio
Calcoliamo l'inversa di A con il metodo di Jordan
A = 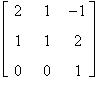
Si considera la matrice 3 x 6 ottenuta affiancando ad A la matrice identica di uguale dimensione
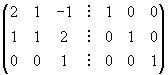
Effettuando operazioni riga elementari si trovanoin sequenza le seguenti matrici:
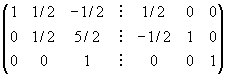
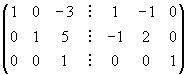
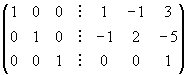
La matrice 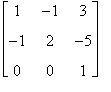 è tale che
è tale che
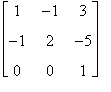
ovvero è l'inversa di A.
Osservazione:
il procedimento indicato permette anche di stabilire l'eventuale non invertibilità della matrice A: se ad un certo passo una riga diviene composta da tutti elementi nulli, allora A è non invertibile.
Fonte: http://www.alessandrobonini.it/download/matematica/Matrici.doc
Autore: non indicato nel documento
Matematica matrici
Visita la nostra pagina principale
Matematica matrici
Termini d' uso e privacy