statistica
statistica
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
statistica
SCHEDE DI STATISTICA
La statistica studia come rappresentare dati e come trarne informazioni.
Definizioni generali
I caratteri sono gli aspetti che si vogliono studiare e possono essere sempre presentati come domande; ad esempio, i quattro caratteri citati sotto possono essere presentati così. Che colore hanno le auto? Qual è il titolo di studio? Qual è l’altezza di un individuo? Quanti sono i componenti delle famiglie?
I caratteri possono essere qualitativi, quando su di essi non è possibile usare le quattro operazioni, o quantitativi, negli altri casi.
I caratteri qualitativi possono essere o ordinati o no; in tal caso, si chiamano sconnessi. Esempio di carattere sconnesso: il colore delle auto; esempio di carattere ordinato: il titolo di studio.
I caratteri quantitativi possono essere continui o discreti. Esempio di carattere continuo: l’altezza di un individuo; esempio di carattere discreto: il numero di componenti di una famiglia.
La popolazione è l’insieme di tutti gli individui che ha un certo carattere.
Il campione è la parte di popolazione viene effettivamente studiata.
In genere, studiare un’intera popolazione è costoso, a volte insensato: si pensi al controllo qualità sui fiammiferi. Per questo bisogna contentarsi di lavorare su campioni.
Le tecniche di scelta di un campione sono argomento di quinta.
Nel seguito ci si limita agli aspetti essenziali della statistica descrittiva, cioè la statistica che si limita a studiare un campione, senza tentare affermazioni sulla popolazione.
Definizioni operative
Una modalità è una delle risposte a una domanda su un carattere. Ad esempio, se il carattere è dato dalla domanda: qual è il titolo di studio? Le modalità sono, per citare le principali: analfabeta, licenza elementare, diploma di scuola media, diploma di maturità, laurea, dottorato di ricerca.
La frequenza (assoluta) è il numero di volte che una certa modalità appare nel campione. Ad esempio, se in una classe il carattere blue jeans appare 12 volte, allora la frequenza della modalità blue jeans è 12.
La frequenza relativa è la percentuale di campione che ha il carattere. Ad esempio, se nella classe ci sono 20 studenti, allora la frequenza relativa della modalità blue jeans è 12/20 = 60%, perciò il 60% del campione indossa blue jeans.
Distribuzioni di frequenza
Una distribuzione di frequenza è l’insieme di tutte le modalità di un carattere, ciascuna associata alla sua frequenza. Ecco un esempio.
|
Modalità |
|||
Carattere: quanti fratelli o sorelle hanno gli studenti di una classe? |
0 |
1 |
2 |
3 |
Frequenza |
8 |
9 |
2 |
1 |
Le distribuzioni di frequenza su caratteri qualitativi vengono chiamate mutabili statistiche.
Le distribuzioni di frequenza su caratteri quantitativi vengono chiamate variabili statistiche.
Se una distribuzione di frequenza è continua (e a volte anche se è discreta), la sua rappresentazione tabulare in genere è data suddividendo il carattere per classi. Ad esempio, se il carattere è quanto sono alti gli studenti di una classe, la distribuzione di frequenza può assumere questo aspetto.
Oltre (in cm) |
140 |
150 |
160 |
170 |
180 |
Fino a (in cm) |
150 |
160 |
170 |
180 |
190 |
Frequenza |
2 |
5 |
6 |
3 |
4 |
Può allora essere utile per i calcoli seguenti ridurre le classi di frequenza ad un valore centrale, dato dalla media fra il limite superiore e quello inferiore. Dato che “oltre x”, in pratica, significa “da x+1”, la distribuzione prende questo aspetto.
Altezza (in cm) |
145,5 |
155,5 |
165,5 |
175,5 |
185,5 |
Frequenza |
2 |
5 |
6 |
3 |
4 |
Rappresentazione grafica delle distribuzioni di frequenza
Si rimanda alle lezioni in laboratorio.
Le medie
Trattare con un insieme di dati non è in genere molto pratico; è più comodo se si riesce a riassumere il valore generale di una distribuzione di frequenza con un solo valore. Questo unico valore rappresentativo si chiama media e, in mancanza di maggiori specifiche, può essere qualunque valore compreso fra le varie modalità.
La moda
Quando si tratta di caratteri sconnessi, è difficile impiegare la matematica; tuttavia, qualcosa si può fare, perché anche per queste modalità esistono le frequenze, che sono numeri. Resta il fatto che questi numeri non presentano in genere alcuna struttura evidente; l’unico aspetto rilevante è che ci sono frequenze maggiori e frequenze minori. In tal caso, il valore che rappresenta meglio il campione è chiaramente la modalità più frequente, che viene chiamata moda.
Esempio: abbiamo la seguente mutabile statistica.
Mutabile: di che colore sono le scarpe degli studenti di una data classe? |
Nero |
Bianco |
Grigio o argentato |
Rosso |
Marrone |
Blu o azzurro |
Frequenza |
8 |
6 |
2 |
1 |
1 |
2 |
In questo caso, la frequenza massima (frequenza modale) è 8, perciò la moda è Nero. In effetti, si può affermare che in quella classe, quel giorno, le scarpe nere sono di moda.
IMPORTANTE: evitare risposte del genere “la moda è 8”! Confondere la modalità della moda con la frequenza modale è GRAVE.
La mediana
Ammettiamo ora di avere a che fare con caratteri ordinati, ma non quantitativi.
Oltre alle frequenze, l’unico aspetto tipicamente matematico qui è l’ordine; si può sfruttare questo aspetto, cercando qual è la modalità “centrale” della distribuzione, cioè quella che divide il campione in una metà maggiore e in una minore o, in altri termini, quella per cui le frequenze totali delle modalità minori e quelle delle maggiori siano uguali.
Tuttavia, spesso una distribuzione non può essere divisa esattamente a metà (basta pensare al caso con 5 atleti giudicati deboli, 3 atleti giudicati medi e 2 atleti giudicati forti; a metà starebbe un atleta giudicato a metà fra debole e medio, che nella distribuzione non esiste).
Come si aggira l’ostacolo? Se le frequenze totali delle modalità minori della mediana sono uguali a quelle delle modalità maggiori, allora la loro differenza è 0. Basta accettare che questa differenza, invece che 0, sia la più vicina possibile a 0, cioè che la differenza in valore assoluto sia minima.
La mediana quindi è la modalità per cui è minima la differenza in valore assoluto fra la frequenza totale delle modalità minori e la frequenza totale delle modalità maggiori.
Ecco come si svolge il calcolo sulla base della definizione.
1 Si scrive la distribuzione di frequenza, mettendo le modalità in ordine crescente (il più tipico) o descrescente (comunque legittimo).
2 Si scrive la colonna delle frequenze cumulate: si tratta di riportare la somma della prima frequenza (cioè la prima frequenza stessa), la somma delle prime due frequenze (cioè la frequenza cumulata appena calcolata+la seconda frequenza), la somma delle prime tre frequenze (cioè la frequenza cumulata appena calcolata+la terza frequenza) e così via, fino alla fine delle frequenze.
3 Si scrive la colonna delle frequenze retrocumulate, che è come la colonna precedente, ma partendo dal basso: si tratta di riportare la somma dell’ultima frequenza (cioè l’ultima frequenza stessa), la somma delle ultime due frequenze (cioè la frequenza cumulata appena calcolata+la penultima frequenza), la somma delle ultime tre frequenze (cioè la frequenza cumulata appena calcolata+la terz’ultima frequenza) e così via, fino all’inizio delle frequenze.
Nota: a rigore, i calcoli ai punti 2 e 3 trovano numeri più grandi delle frequenze minori e maggiori di una certa modalità, ma le parti eccedenti si elidono nel calcolo al punto 4.
4 Si scrive la differenza delle due colonne appena trovate e se ne prende il valore assoluto.
5 Si guarda qual è il minimo di questi valori assoluti.
6 La modalità che sta sulla stessa riga di questa differenza minima è la mediana.
Esempio: è data la seguente distribuzione di frequenza, non ordinata.
|
Modalità |
||||||
Carattere: quanti sono i morti per incidente in ogni giorno della settimana? |
Dom |
Gio |
Lun |
Mar |
Mer |
Sab |
Ven |
Frequenze |
770 |
497 |
447 |
464 |
444 |
703 |
510 |
Dati Istat 2002.
I dati sono in ordine alfabetico sui giorni della settimana, che è un ordine poco sensato. Per i calcoli, rimettiamo tutto in ordine cronologico. La tabella con i calcoli è questa.
Modalità x |
Frequenze f |
Cumulate F |
Retrocumulate R |
Differenza in valore assoluto D |
Lun |
447 |
447 |
3835 |
3388 |
Mar |
464 |
911 |
3388 |
2477 |
Mer |
444 |
1355 |
2924 |
1569 |
Gio |
497 |
1852 |
2480 |
628 |
Ven |
510 |
2362 |
1983 |
379 |
Sab |
703 |
3065 |
1473 |
1592 |
Dom |
770 |
3835 |
770 |
3065 |
La differenza minima è 379, che corrisponde a venerdì, che quindi è il giorno mediano.
Lo schema generale è il seguente. Viene introdotto il simbolo S (sigma maiuscolo, la esse greca), che indica la somma di molti dati e viene chiamata sommatoria.
Modalità x |
Frequenze f |
Cumulate F |
Retrocumulate R |
Differenza in valore assoluto D |
x1 |
f1 |
F1 = Sf da 1 a 1, cioè f1 |
R1 = Sf da n a 1, cioè R2+f1 |
D1 = |F1-R1| |
x2 |
f2 |
F2 = Sf da 1 a 2, cioè F1+f2 |
... |
D2 = |F2-R2| |
... |
... |
... |
Rn-1 = Sf da n a n-1, cioè Rn+fn-1 |
... |
xn |
fn |
Fn = Sf da 1 a n, cioè Fn-1+fn |
Rn = Sf da n a n, cioè fn |
Dn = |Fn-Rn| |
In effetti, può esserci anche più di una modalità mediana; il caso più semplice si ha con un numero pari di modalità, tutte con la stessa frequenza; ecco un esempio.
Modalità x |
Frequenze f |
Cumulate F |
Retrocumulate R |
Differenza in valore assoluto D |
A |
1 |
1 |
6 |
5 |
B |
1 |
2 |
5 |
3 |
C |
1 |
3 |
4 |
1 |
D |
1 |
4 |
3 |
1 |
E |
1 |
5 |
2 |
3 |
F |
1 |
6 |
1 |
5 |
Poco importa sapere di che carattere si stia trattando. Si nota subito che la colonna delle differenze ha due valori minimi, pertanto ci sono due modalità mediane, la C e la D. Trattandosi di un carattere ordinato e non quantitativo, non si può trovare una loro posizione intermedia: non c’è qualcosa come “C e mezzo”. Questo sarebbe possibile soltanto con un carattere quantitativo, ma in tal caso ci sono indici che danno maggiori informazioni della mediana, cioè i seguenti.
La media aritmetica semplice
Quando un carattere è quantitativo, diventa possibile usarlo nei calcoli, per trovare altre medie. La media più comune è quella aritmetica, cioè quel valore che, sostituito ai dati (le modalità quantitative si chiamano solitamente così), non cambia la loro somma.
Si tratta quindi di trovare il valore M per cui è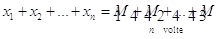 
o, usando il simbolo di sommatoria,
.
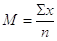La media aritmetica ponderata
Naturalmente, quanto appena esposto è vero per dati che appaiono una volta sola, cioè con frequenza 1.
Nel caso in cui la frequenza sia diversa da 1, come è normale nelle distribuzioni di frequenza, bisogna pensare che ogni dato x con frequenza f potrebbe essere scritto come f dati, tutti uguali, ciascuno con frequenza 1; ognuno di questi dati x andrebbe contato f volte, perciò il suo valore complessivo è xf.
Ciò significa anche che il numero totale n dei dati si ottiene non contando soltanto i dati diversi, ma tutti i dati, cioè sommando tutte le frequenze.
Esempio: si ha questa distribuzione di frequenza.
x: quante auto possiedono gli individui del campione? |
0 |
1 |
2 |
3 |
f |
3 |
13 |
5 |
1 |
La media aritmetica ponderata è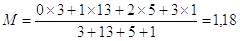 
. Si noti che NON è (0+1+2+3)/4. In un calcolo simile si farebbe la media dei dati diversi, non di tutti i dati!
La formula generale è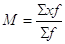 
.
IMPORTANTE: ci sono poche cose più gravi che non saper calcolare una media aritmetica ponderata, magari confondendo dati e frequenze.
Proprietà delle medie aritmetiche
Sono utili 3 proprietà delle medie aritmetiche, ponderate o no, che si indicheranno con M(x), cioè media aritmetica sui dati x1 , x2 , ..., xn .
Proprietà di banalità: la media di dati tutti uguali è il dato stesso. Infatti, se il dato vale k, si ha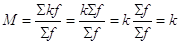 
Sf. La proprietà si può scrivere come M(k) = k.
Proprietà di omogeneità: se tutti i dati sono moltiplicati per una costante a, allora anche la media è moltiplicata per la costante a. Infatti, si ha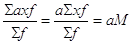 
.
In altri termini: se cambio unità di misura ai dati, devo cambiare coerentemente unità di misura anche alla media. La proprietà si può scrivere come M(ax) = aM(x).
Esempio: devo fare la media di 4000, 3000 e 6000. Faccio la media di 4, 3 e 6 e poi moltiplico per 1000, che è la mia costante a.
Proprietà di additività: facendo la media della somma di due variabili, x e y, con le stesse frequenze, si ottiene la somma delle due medie. Infatti, si ha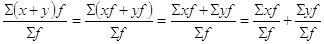 
Syf.
La proprietà si può scrivere come M(x+y) = M(x)+M(y).
Esempio: devo fare la media di 17,46, 12,46 e 13,46. Faccio la media di 7, 2 e 3 e poi aggiungo 10,46. Qui si è impiegata la terza proprietà, ponendo y = 10,46, ma anche la prima, notando che è y = k.
La media geometrica
Sempre impiegando lo stesso principio impiegato per la media aritmetica, si definisce come media geometrica quel valore che, sostituito ai dati, non cambia il loro prodotto.
Si tratta quindi di trovare il valore G per cui è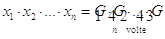 
, cioè per cui è Gn = x1x2...xn , cioè per cui è
G = nÖ(x1x2...xn).
L’uso principale della media geometrica è nel calcolo del tasso d’interesse composto medio o, più in generale, nei tassi di variazione per una data grandezza. Infatti, quando si calcola un montante W (non uso M, che qui indica la media aritmetica) partendo da un capitale C mediante la composizione di tassi d’interesse r1 , r2 , ..., rn , che variano in ogni periodo, si ottiene la formula W = C(1+r1)(1+r2)...(1+rn). Un tasso medio corretto G deve svolgere la stessa funzione che svolgono i vari tassi r1 , r2 , ..., rn , perciò dev’esser tale che sia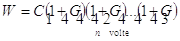 
-1.
Esempio: qual è la media dei tassi composti 3%, 2% e 7%?
È G = 3Ö[(1+0,03)(1+0,02)...(1+0,07)]-1 = 0,0398 = 3,98%.
La media aritmetica avrebbe dato il risultato scorretto 4%.
Esempio: nella prima ora, una vasca perde il 2% del liquido contenuto, nella seconda ora il 3% e nella terza ora il 9%. Quando perde in media all’ora la vasca?
È G = 3Ö[(1-0,02)(1-0,03)...(1-0,09)]-1 = -0,0472 = -4,72%.
I segni negativi sono dovuti al fatto che la vasca perde, pertanto si ha una diminuzione.
La media geometrica ponderata è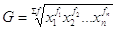 
, per ragionamenti simili a quelli adottati ponderando la media aritmetica.
La media armonica
La media armonica è quel valore che, sostituito ai dati, non cambia la somma dei loro reciproci. Si tratta quindi di trovare il valore A per cui è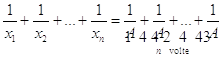 
, cioè per cui è
.
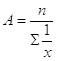Una simile media ha un aspetto artificioso e sembra dovuta al puro gusto di complicarsi la vita, ma non è così, come mostra il seguente classico esempio.
Esempio: da Milano a Torino ci sono circa 150 km; se andando da Milano a Torino impiego 3 ore, la velocità dell’andata è di 50 km/h. Poniamo ora che la velocità media fra andata e ritorno sia di 25 km/h; allora, l’uso della media aritmetica porterebbe alla seguente equazione: (50+x)/2 = 25. Risolvendo, si trova subito x = 0. Il che significa che la velocità del ritorno sarebbe 0 km/h, cioè che si tornerebbe stando fermi!
Evidentemente, la media aritmetica è una scelta infelice. Ma qual è la media corretta?
Dato che la distanza da Milano a Torino fra andata e ritorno non cambia, la si può indicare con il solo simbolo s (come spazio). I tempi di percorrenza dell’andata e del ritorno invece possono essere diversi, perciò li si indicherà rispettivamente con tA e tR . Dato che la velocità è spazio fratto tempo, le velocità di andata e ritorno si possono scrivere come vA = s/tA e vR = s/tR , mentre la velocità media può essere scritta come vM = s/tM . Per calcolare la velocità media, bisogna dunque determinare il tempo medio tM .
Dato che il tempo complessivo impiegato nell’andata e nel ritorno dev’essere uguale alla somma dei due tempi medi, qui si può, anzi si deve, usare la media aritmetica: è tM = (tA+tR)/2; quindi la velocità media è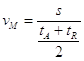 
. Con pochi passaggi si trova ora che la velocità media è la media armonica delle velocità:
.
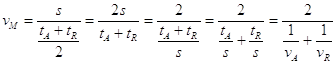Nel nostro esempio, la velocità del ritorno sarebbe vR = 16,67 km/h.
La media armonica ponderata è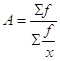 
, per ragionamenti simili a quelli adottati ponderando la media aritmetica.
La varianza e lo scarto quadratico medio
Cominciamo con un sonetto di Trilussa, il cui significato viene solitamente distorto e svilito in una gratuita avversione verso il pensiero statistico, mentre risulta evidente dal testo che il significato è la critica verso le statistiche di regime, che nascondono le disuguaglianze.
LA STATISTICA
Sai ched’è la statistica? E’ ’na cosa
che serve pe’ fa’ un conto in generale
de la gente che nasce, che sta male,
che more, che va in carcere e che sposa.
Ma pe’ me la statistica curiosa
è dove c’entra la percentuale,
pe’ via che, lì, la media è sempre eguale
puro co’ la persona bisognosa.
Me spiego: da li conti che se fanno
secondo le statistiche d’adesso
risurta che te tocca un pollo all’anno:
e, se nun entra ne le spese tue,
t’entra ne la statistica lo stesso
perché c’è un antro che ne magna due.
La parte che interessa qui è quella che ho posto in corsivo. Se una persona ha due polli e un’altra nessuno, in media (aritmetica, che è quella che si userà nel seguito) le due persone hanno un pollo a testa. In una simile situazione, la media (e non l’intero mondo della statistica!) ha poco significato, perché la differenza fra la media e la realtà delle due persone è enorme: è grande addirittura come la media stessa.
Serve allora un indice che misuri quando i dati veri sono lontani dalla media e quindi che ne misuri l’insignificanza. L’indice più naturale sembra la distanza media fra i dati e la loro media aritmetica. Procediamo a calcolarlo con l’esempio di Trilussa.
x: polli a testa |
f |
xf |
x-M |
(x-M)f |
0 |
1 |
0 |
-1 |
-1 |
2 |
1 |
2 |
1 |
1 |
S |
2 |
2 |
|
0 |
La media è M = 2/2 = 1; la distanza media è 0/2 = 0.
Quest’ultimo risultato è inverosimile. In realtà, il calcolo della distanza media svolto in questo modo dà sempre come risultato 0.
Lo si dimostra facilmente usando le proprietà della media aritmetica: stiamo calcolando M(x-M), ma questo porta a M(x-M) = M(x)-M(M) = M-M = 0.
Senza qualche miglioramento, la distanza media non dà niente. Ma come intervenire?
Se si guarda lo specchietto, si nota che l’ultima colonna porta ad un totale nullo perché ci sono termini negativi. Basterebbe che questi venissero neutralizzati e il problema sparirebbe. I modi più comuni di eliminare un segno meno sono due: o si prende il numero in valore assoluto o lo si eleva al quadrato.
Prendere i numeri in valore assoluto porta a volte a qualche difficoltà di calcolo e comunque si è sperimentato che implica poche proprietà matematiche comode e utili, perciò si prendono i dati al quadrato. Il calcolo allora diventa così.
x: polli a testa |
f |
xf |
(x-M)2 |
(x-M)2f |
0 |
1 |
0 |
1 |
1 |
2 |
1 |
2 |
1 |
1 |
S |
2 |
2 |
|
2 |
La distanza media che risulta da questi calcoli, chiamata varianza, è allora VAR = 2/2 = 1.
Tuttavia, la varianza contiene la somma di numeri al quadrato e rappresenta una specie di distanza media su polli al quadrato, che nessuno sa che cosa siano. Perciò bisogna tornare all’unità di misura originaria, prendendo la sua radice, che si chiama scarto quadratico medio. Si ha quindi SQM = Ö1 = 1 (naturalmente, 1 è l’unico numero insieme allo 0 per cui l’effetto della radice è invisibile).
Si ottiene allora quello che indica il buon senso: che la distanza fra la media e la realtà, cioè lo scarto quadratico medio, è uguale alla media stessa, perciò è abbastanza grande da rendere la media ben poco significativa.
Quindi è proprio la statistica che rimedia all’assurdità di impiegare la sola media, che è il modo in cui qualcuno fa statistica secondo Trilussa, ma è anche il modo in cui si sbaglia a fare statistica secondo gli statistici.
Finora si è proceduto a furia di calcoli; ecco le formule della varianza e dello scarto quadratico medio, che li riassumono.
;
.
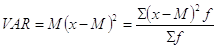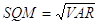La formula ridotta della varianza
La varianza può essere calcolata anche in un modo leggermente più semplice, tramite la formula ridotta, che si ottiene con questi passaggi.
VAR = M(x-M)2 = M(x2+M2-2xM) = M(x2)+M(M2)-2M(xM) = M(x2)+M2-2MM(x) = M(x2)+M2-2M2 = M(x2)-M2.
In parole: la varianza è la media dei quadrati meno il quadrato della media.
Esempio: finora si sono usati i dati schematici dell’esempio di Trilussa. Si passi ora a qualcosa di più significativo, come la seguente distribuzione di frequenza. La fonte è http://www.fondazionenordest.net/uploads/media/B6_marzo_2007.pdf. Il reddito di cui si tratta è l’imponibile Irpef (dichiarato del 2005 per il 2004) per i comuni del Nord Est con oltre 30.000 abitanti nel 2004.
Classi di reddito |
|
|
Da |
Fino a |
Frequenza |
- |
1.000 |
7.994 |
1.000 |
2.000 |
7.907 |
2.000 |
3.000 |
6.981 |
3.000 |
4.000 |
6.900 |
4.000 |
5.000 |
8.316 |
5.000 |
6.000 |
9.244 |
6.000 |
7.500 |
16.823 |
7.500 |
10.000 |
85.291 |
10.000 |
15.000 |
242.829 |
15.000 |
20.000 |
276.151 |
20.000 |
25.000 |
195.817 |
25.000 |
29.000 |
99.550 |
29.000 |
32.600 |
56.032 |
32.600 |
35.000 |
25.771 |
35.000 |
40.000 |
36.210 |
40.000 |
50.000 |
40.303 |
50.000 |
60.000 |
22.891 |
60.000 |
70.000 |
15.931 |
70.000 |
100.000 |
23.078 |
100.000 |
115.866,7835 |
18.296 |
Il limite superiore dell’ultima classe di reddito è stato introdotto da me per far tornare i conti sul dato medio, come fornito dalla fonte.
Per i calcoli successivi, bisogna trovare un solo reddito per classe; si prende, come è convenzione, il reddito centrale. La delimitazione delle classi fornita dal sito non è chiarissima, ma di regola il limite inferiore “Oltre” indica che è aperto, perciò “Da” dovrebbe essere chiuso. Quindi è aperto il limite superiore.
Per comodità, conviene poi dividere questo reddito per 1000. Si ottiene allora la seguente tabella.
x/1000 |
f |
xf |
(x-M)2f |
x2f |
0 |
7.994,00 |
- |
4.368.967,98 |
- |
1,5 |
7.907,00 |
11.860,50 |
3.784.661,00 |
17.790,75 |
2,5 |
6.981,00 |
17.452,50 |
3.042.954,33 |
43.631,25 |
3,5 |
6.900,00 |
24.150,00 |
2.726.430,77 |
84.525,00 |
4,5 |
8.316,00 |
37.422,00 |
2.963.646,88 |
168.399,00 |
5,5 |
9.244,00 |
50.842,00 |
2.954.594,02 |
279.631,00 |
6,75 |
16.823,00 |
113.555,25 |
4.651.397,87 |
766.497,94 |
8,75 |
85.291,00 |
746.296,25 |
18.250.430,98 |
6.530.092,19 |
12,5 |
242.829,00 |
3.035.362,50 |
28.734.171,56 |
37.942.031,25 |
17,5 |
276.151,00 |
4.832.642,50 |
9.541.261,99 |
84.571.243,75 |
22,5 |
195.817,00 |
4.405.882,50 |
150.952,28 |
99.132.356,25 |
27 |
99.550,00 |
2.687.850,00 |
1.305.984,72 |
72.571.950,00 |
30,8 |
56.032,00 |
1.725.785,60 |
3.086.583,25 |
53.154.196,48 |
33,8 |
25.771,00 |
871.059,80 |
2.799.196,51 |
29.441.821,24 |
37,5 |
36.210,00 |
1.357.875,00 |
7.221.392,05 |
50.920.312,50 |
45 |
40.303,00 |
1.813.635,00 |
18.842.090,72 |
81.613.575,00 |
55 |
22.891,00 |
1.259.005,00 |
22.889.875,32 |
69.245.275,00 |
65 |
15.931,00 |
1.035.515,00 |
27.598.718,84 |
67.308.475,00 |
85 |
23.078,00 |
1.961.630,00 |
87.633.416,74 |
166.738.550,00 |
115,8667835 |
18.296,00 |
2.119.898,67 |
156.507.187,14 |
245.625.840,34 |
Somme |
1.202.315,00 |
28.107.720,07 |
409.053.914,10 |
1.066.156.193,94 |
La media è M = 28.107.720,07/1.202.315 = 23,378; pertanto, il reddito medio è 23,378´1000 = 23.378 euro.
La varianza si può ottenere in due modi.
* Con la formula diretta, per cui serve calcolare la colonna intestata con (x-M)2f, arrivando a trovare VAR = 409.053.914,1/1.202.315,00 = 340,2219.
* Con la formula ridotta (consigliato), per cui serve calcolare la colonna intestata con x2f, arrivando a trovare M(x2) = 1.066.156.193,94/1.202.315,00 = 886,752801 e poi VAR = 886,752801-23,3782 = 340,2219.
In ogni caso, lo scarto quadratico medio è SQM = Ö340,2219 = 18,4451055. Tornando agli euro, è SQM = 18,4451055´1000 = 18.445,51.
Quindi: nei grandi comuni del Nord Est, il reddito medio è 23.378 euro; in media, ci si scosta da questo reddito, in più o in meno, di 18.445,51 euro. La situazione è un po’ diversa da quella azzardata da Trilussa, ma c’è comunque una disuguaglianza accentuata fra i redditi; in termini statistici, ciò significa che il reddito medio di questa realtà è un’informazione poco significativa.
Va infine segnalato che lo scarto quadratico medio non è una misura ideale per misurare la concentrazione dei redditi, per motivi che esulano dalla lezioni in un istituto superiore. Esistono molti altri indici con proprietà migliori. Gli interessati possono cominciare da
http://it.wikipedia.org/wiki/Indice_di_concentrazione_di_Gini o da
http://www.economia.unimi.it/courses/Economia_Istruzione/Disuguaglianza_D.pdf.
Fonte: http://schedematematica.wikispaces.com/file/view/SCHEDE%20DI%20STATISTICA.doc
Sito web da visitare :http://schedematematica.wikispaces.com/
Autore del testo: non indicato nel documento di origine
Parola chiave google : statistica tipo file : doc
Visita la nostra pagina principale
statistica
Termini d' uso e privacy