Funzioni goniometriche
Funzioni goniometriche
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Funzioni goniometriche
LE FUNZIONI GONIOMETRICHE
Consideriamo un sistema di assi cartesiani e una circonferenza con il centro coincidente con l’origine degli assi e il raggio unitario (r =1). Tale circonferenza viene detta circonferenza goniometrica (fig.1).
Sulla circonferenza goniometrica consideriamo un punto P, tale che il raggio OP formi con l’asse delle x l’angolo orientato a (a è positivo se forma una rotazione antioraria rispetto a x).
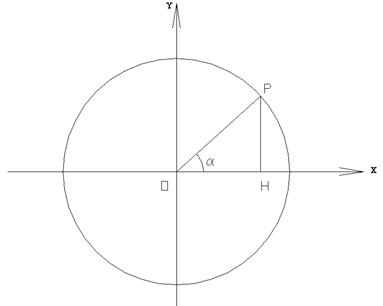
FIG.1
Il punto P ha coordinate: Pº(OH; PH)
Si definisce seno dell’angolo a l’ordinata del punto P:
sen a=PH.
Si definisce coseno dell’angolo a l’ascissa del punto P:
cos a=OH
Prolunghiamo il raggio OP e chiamiamo P2 l’intersezione di tale prolungamento con la retta tangente alla circonferenza del punto P1 di incontro tra la circonferenza e l’asse delle x (fig.2)
Si definisce tangente dell’angolo a l’ordinata del punto P2:
P2P1=tan a
P2P1=tg a
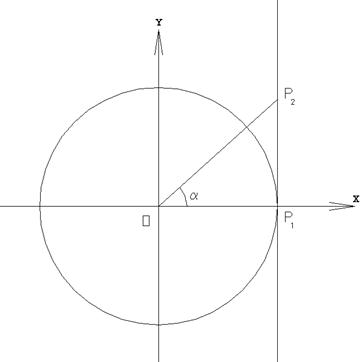
FIG.2
Consideriamo ora la tangente alla circonferenza goniometrica portata per il punto A1 di intersezione tra la circonferenza e l’asse delle ordinate. Indichiamo inoltre con A2 l’intersezione tra tale tangente e il prolungamento del raggio OP (FIG.3).
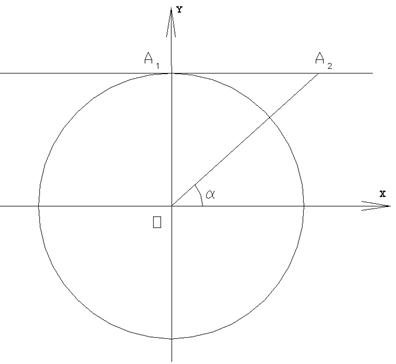
FIG.3
Si definisce cotangente dell’angolo a l’ascissa del punto A2:
A1A2=cotana
A1A2=cotga.
Conduciamo una tangente alla circonferenza goniometrica nel punto P (vedi FIG.4). Il raggio OP formi con l’asse delle x l’angolo orientato a .
Se chiamiamo S l’eventuale punto d’incontro tra la suddetta tangente e l’asse delle ascisse e S’ l’eventuale punto d’incontro con l’asse delle ordinate, si definisce secante dell’angolo a l’ascissa del punto S :
OS=sec a .
Si definisce cosecante dell’angolo a l’ordinata del punto S’ :
OS’=cosec a .
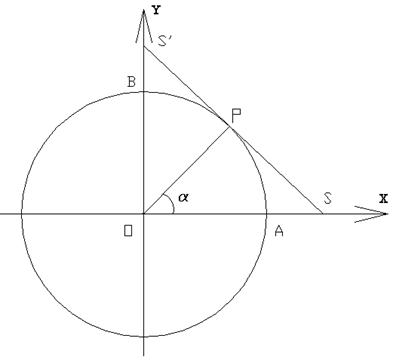
FIG.4
VARIABILITA’ DELLA FUNZIONE SENO
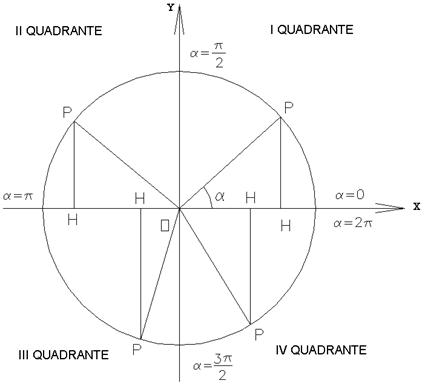
FIG.5
Nel primo quadrante il seno dell’angolo è sempre positivo, coincidente con l’ordinata PH del punto P. In particolare quando a è zero, è zero anche PH, quindi nullo risulta essere il seno di zero.
All’aumentare dell’angolo a aumenta anche PH e quindi il seno dell’angolo. Al limite del primo quadrante a diviene p/2, PH coincide con il raggio, il seno di p/2 è quindi uno, poiché il raggio è pari ad uno.
Sintetizzando possiamo affermare che nel primo quadrante l’angolo va da zero a p/2, il seno dell’angolo è positivo e cresce dal valore zero (sen 0 = 0) al valore 1 (sen p/2 =1 ).
Nel secondo quadrante l’angolo passa dal valore p/2 a p. Il seno è anche in esso positivo, in quanto le ordinate PH sono positive. In particolare a p/2 il seno vale 1, coincidendo PH con il raggio unitario. Aumentando l’angolo a da p/2 a p l’ordinata PH diminuisce, per cui diminuisce anche il seno dell’angolo. Alla fine del secondo quadrante l’angolo diviene p, PH si annulla e diviene 0 anche il seno di p.
In sintesi nel secondo quadrante il seno è positivo e decresce, passando dal valore 1 (sen p/2 = 1) al valore 0 (sen p = 0).
Nel terzo quadrante l’angolo passa da p a 3p/2, il seno è negativo, in quanto l’ordinata PH è negativa. In particolare a p PH è nulla, il seno è nullo. Man mano che cresce l’angolo il segmento PH aumenta, ma, poiché l’ordinata è negativa, il seno decresce. A 3p/2 (limite del quadrante) PH diviene -1.
In sintesi nel terzo quadrante il seno è negativo e decresce passando da 0 (sen p = 0) a -1 (sen 3p/2 = -1).
Nel quarto quadrante il seno è negativo, in quanto PH è negativo. Il seno cresce perché PH passa dal valore -1 a 3p/2 al valore 0 a 2p.
Sintetizzando in esso il seno è negativo e passa dal valore -1 (sen 3p/2=-1) al valore 0 (sen 2p=0).
|
a |
Sen a |
I QUADRANTE |
0 £a£ p/2 |
Da 0 a 1 |
II QUADRANTE |
p/2 £a£ p |
Da 1 a 0 |
III QUADRANTE |
p £a£ 3p/2 |
Da 0 a -1 |
IV QUADRANTE |
3p/2 £a£ 2p |
Da -1 a 0 |
Rappresentiamo ora la funzione seno in un diagramma (la sinusoide FIG.6), che presenta sull’asse delle ascisse gli angoli, su quello delle ordinate i seni degli angoli. Come abbiamo visto in precedenza, il seno assume valore minimo -1 e massimo 1 (varia tra -1 e 1), per cui possiamo disegnare sul diagramma una fascia tra -1 e 1 oltre la quale non può esistere la funzione seno.
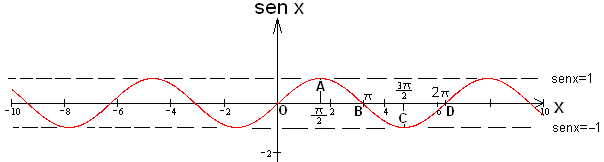
FIG.6
In sequenza le coordinate dei punti O,A,B,C,D, sono
Oº(0;sen0)º(0;0)
Aº(p/2;senp)º(p/2;1)
Bº(p;senp)º(p;0)
Cº(3p/2;sen3p/2)º(3p/2;-1)
Dº(2p;sen2p)º(2p;0)
Unendo con una curva appropriata i punti indicati in figura si ottiene la “sinusoide”. In realtà essa va continuata nella stessa maniera ad intervalli di 2p (si dice che la funzione seno è di periodo 2p), infatti ogni 2p in seno presenta gli stessi risultati.
Due angoli sono congruenti quando si differenziano dalla quantità di 2p o multipla di 2p. Ad esempio p/2 e 5p/2 (p/2+2p) sono congruenti perché si differenziano di 2p ed hanno lo stesso valore del seno.
VARIABILITA’ DELLA FUNZIONE COSENO
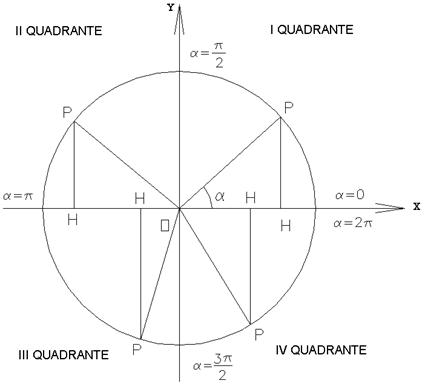
FIG.7
Sappiamo che il coseno di un angolo è l’ascissa di un punto P che si trova sulla circonferenza goniometrica (nel caso in figura il segmento OH).
Nel primo quadrante il segmento OH è positivo, in particolare quando a è 0, OH coincide con il raggio unitario e il coseno è 1 (cos0=1).
Man mano che cresce a, diminuisce il segmento OH e quindi il coseno di a. Quando è p/2, OH diviene 0, nullo risulta quindi essere il coseno di p/2 (cosp/2=0).
In sintesi il coseno del primo quadrante è positivo e decrescente, passando dal valore 1 a 0, al valore 0 a p/2.
Nel secondo quadrante il segmento OH diviene negativo, per cui il coseno è negativo e passa dal valore 0 per a pari a p/2 (cosp/2=0) al valore -1 per a=p (cosp=-1).
Il coseno quindi decresce passando da 0 a -1.
Sintetizzando il coseno del secondo quadrante è negativo e decrescente passando dal valore 0 a p/2 al valore -1 a p.
Nel terzo quadrante il coseno è negativo, crescente dal valore -1 per a=p al valore 0 per a=3p/2.
Nel quarto quadrante il segmento OH torna ad essere positivo, per cui positivo è il coseno. Esso inoltre è crescente, poiché passa dal valore 0 per a=3p/2 (cos3p/2=0) al valore 1 per a=2p (cos2p=1).
Sintetizzando nel quarto quadrante il coseno è positivo e crescente passando dal valore 0 a 3p/2 al valore 1 a 2p.
La seguente tabella contiene tutto ciò che abbiamo detto:
|
a |
cosa |
I QUADRANTE |
0 £a£ p/2 |
Da 1 a 0 |
II QUADRANTE |
p/2 £a£ p |
Da 0 a -1 |
III QUADRANTE |
p £a£ 3p/2 |
Da -1 a 0 |
IV QUADRANTE |
3p/2 £a£ 2p |
Da 0 a 1 |
Rappresentiamo ora funzione coseno in un diagramma (cosinusoide), che presenta sull’asse delle ascisse gli angoli e su quello delle ordinate il coseno degli angoli. Come per la funzione seno anche il coseno varia tra -1 e 1 (-1 valore minimo, 1 valore massimo) per cui anche in questo caso tracciamo una fascia tra -1 ed 1 oltre la quale il coseno non può esistere.
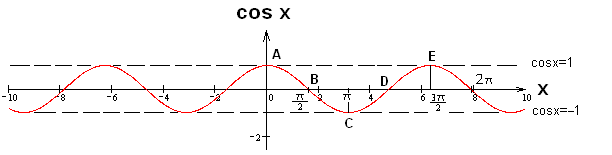
FIG.8
In sequenza le coordinate dei punti A,B,C,D,E sono:
Aº(0;cos0)º(0;1)
Bº(p/2;cosp/2)º(p/2;0)
Cº(p;cosp)º(p;-1)
Dº(3p/2;cos3p/2)º(3p/2;0)
Eº(2p;cos2p)º(2p;1)
Unendo con una curva appropriata I punti individuati in figura si ottiene la “cosinusoide”.
Anche la cosinusoide come la sinusoide va continuata identica a se stessa ad intervalli di 2p. Per questo motivo possiamo affermare che anche il coseno ha periodo 2p, presentando ogni 2p gli stessi valori.
È interessante confrontare la sinusoide con la cosinusoide.
Come si può osservare le due curve sono identiche e sfasate di p/2.
VARIABILITA’ DELLA FUNZIONE TANGENTE
Come si può osservare nella figura 9 A nel primo quadrante la tangente dell’angolo è positiva. In particolare quando a è nullo il segmento PH, che rappresenta la tangente diviene 0 (P coincidente con H). Man mano che a cresce (a3>a2>a1>a Þ P3H>P2H>P1H>PH) cresce la tangente.
Man mano che a si avvicina a p/2 la tangente tende a diventare grandissima. Quando a diviene 90° il punto P tende all’infinito, in quanto il segmento OP tende a diventare parallelo alla tangente.
Possiamo dire che a p/2 la tangente dell’angolo è più infinito (+¥).
In sintesi possiamo dire che nel primo quadrante la tangente è positiva, crescente dal valore 0 (tan0=0) a +¥ (tanp/2=+¥).
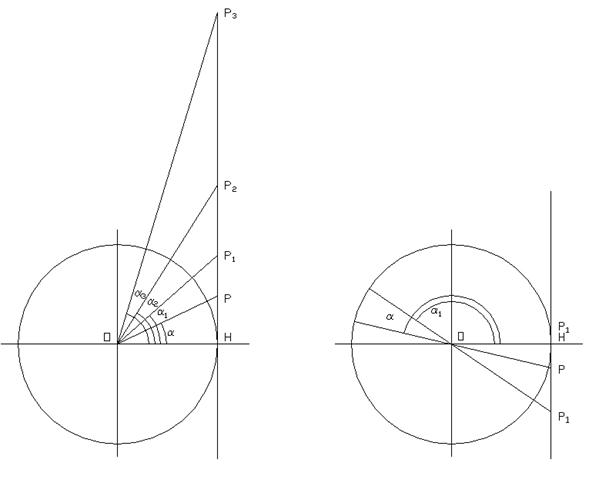
FIG. 9 A FIG. 9 B
Per comprendere meglio la variabilità della funzione tangente nel secondo quadrante partiamo da p e torniamo a ritroso verso p/2 (figura 9 B) . A p il punto coincide con H, quindi la tangente è nulla. Man mano che l’angolo decresce, passando da a ad a1 , la tangente in valore assoluto cresce (P1H>PH), ma in realtà decresce poiché è negativa.
Man mano che si avvicina l’angolo a p/2 (da sinistra) l’ordinata del punto P corrispondente sulla tangente diventa un numero negativo sempre più grande. In particolare la tangente a p/2 è meno infinito (-¥), in quanto il segmento OP tende a diventare parallelo alla tangente.
Sintetizzando nel secondo quadrante la tangente è crescente, negativa e passa dal valore -¥ (tanp/2=-¥) al valore 0 (tanp=0).
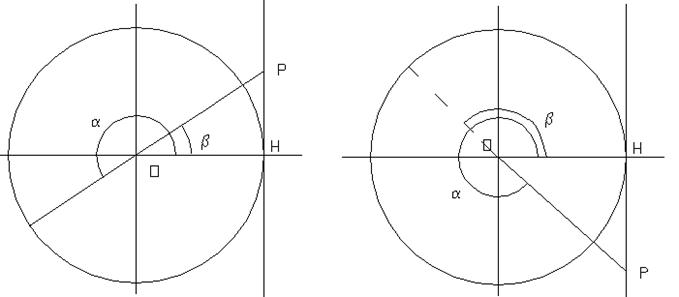
FIG. 10 A FIG. 10 B
Come si può osservare dalla figura 10 A l’angolo a del terzo quadrante ha la stessa tangente PH dell’angolo del primo quadrante. In particolare possiamo scrivere che a=p+b
tana= tan(p+b)= tanb.
Per questo motivo da p a 3p/2 si ripropongono gli stessi valori della tangente riscontrati da 0 a p/2.
In sintesi, quindi, possiamo dire che nel terzo quadrante la tangente è positiva e crescente e passa dal valore 0 (tanp=0) a +¥ (tan3p/2=+¥).
Osservando la figura 10 B , possiamo dedurre che la tangente dell’angolo a del quarto quadrante (segmento PH) coincide con la tangente dell’angolo b del secondo quadrante.
Infatti è: a=p+b
tana= tan(p+b)= tanb.
Nel quarto quadrante, quindi si propongono gli stessi valori del secondo quadrante, per cui, sintetizzando, possiamo affermare che in esso la tangente cresce ed è negativa e passa dal valore -¥ (tan3p/2=-¥) al valore 0 (tan2p=0).
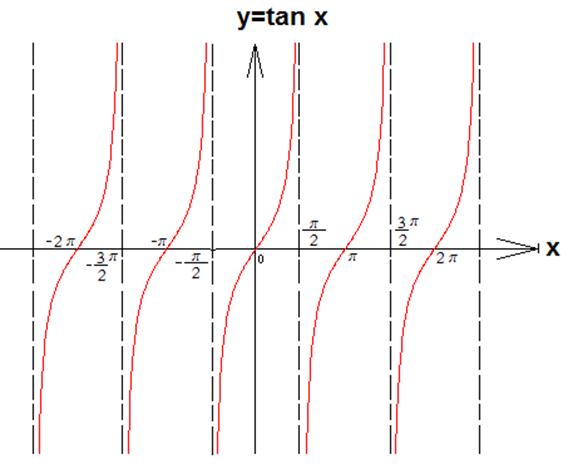
FIG. 11
Riportiamo i valori 0 della tangente a 0, p e 2p e i valori +¥ e -¥ a p/2 e 3p/2 (FIG.11). Si ottiene la tangendoide. Come si può osservare due rami che hanno gli stessi valori distano di p, per cui possiamo affermare che la funzione tangente ha periodo p. Per completare la tangendoide si prosegue il grafico in modo identico ogni p.
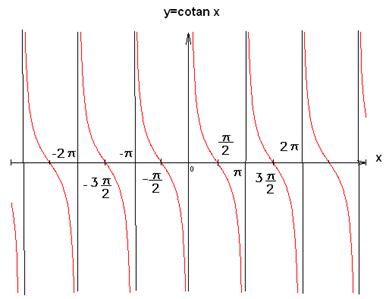
VARIABILITA’ DELLA FUNZIONE COTANGENTE
Come sappiamo, la cotangente dell’angolo a coincide con il segmento PH della figura 12 A. Per questo motivo possiamo affermare che la cotangente nel primo quadrante è positiva. Per semplificare lo studio della cotangente nel primo quadrante, partiamo dall’angolo p/2 e, a ritroso andiamo verso l’angolo 0. A p/2 il segmento PH è nullo, per cui risulta la cotangente di p/2 uguale a 0. Man mano che decresce l’angolo andando verso 0 il segmento PH cresce, la cotangente quindi diventa più grande. Quando l’angolo tende a 0, il segmento PH tende verso l’infinito, in quanto il segmento OP tende a disporsi parallelamente alla retta cui si individua la cotangente.
La cotangente a 0 è quindi +¥.
Sintetizzando, si può affermare che nel primo quadrante la cotangente è positiva e decrescente, passando dal valore +¥ a 0 (cotg0=+¥) al valore 0 a p/2 (cotgp/2=0).
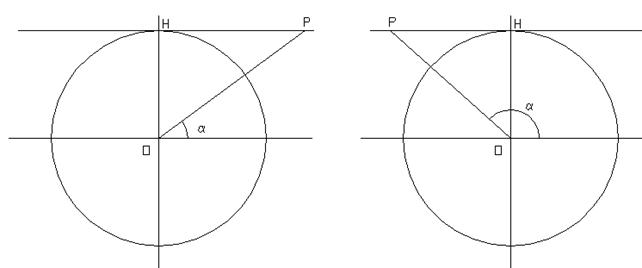
FIG. 12 A FIG. 12 B
Nel secondo quadrante (FIG. 12 B) il segmento PH che rappresenta la cotangente è negativo, la cotangente, quindi, è negativa. In particolare a p/2 PH è nullo ed è nulla anche la cotangente, crescendo a PH diviene un numero negativo sempre più grande e la cotangente decresce. Avvicinandosi a a p, il segmento PH tende a divenire un numero negativo infinitamente grande e il segmento PO tende ad essere parallelo alla retta su cui giace la cotangente. A p, quindi, la cotangente è -¥.
In sintesi, nel secondo quadrante la cotangente è negativa, decrescente e passa dal valore 0 a p/2 (cotgp/2=0) al valore -¥ a p (cotgp=-¥).
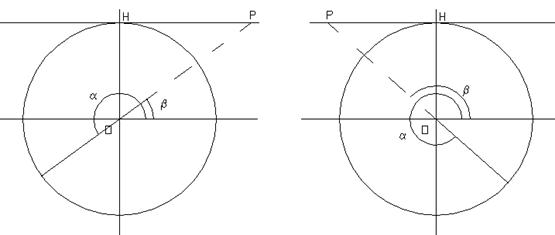
FIG. 13 A FIG. 13 B
Osservando la figura 13 A , si nota che l’angolo a del terzo quadrante corrisponde a quello b del primo, per cui in esso si ripropongono gli stessi valori della cotangente nel primo quadrante. Si ha, quindi, sintetizzando che la cotangente del terzo quadrante è negativa e decrescente e passa dal valore +¥ a p (cotgp=+¥) al valore 0 a 3p/2 (cotg3p/2=0).
L’angolo a del quarto quadrante (fig. 13 B) ripropone gli stessi valori del secondo quadrante relativi all’angolo b, per cui si ha la perfetta coincidenza fra questi due quadranti in relazione alla funzione cotangente.
Sintetizzando si ha quindi che nel quarto quadrante la cotangente è negativa e decrescente e passa dal valore a 3p/2 (cotg3p/2=0) al valore -¥ a 2p (cotg2p=-¥).
Sia per la tangente che per la cotangente, quindi si ha che:
tana= tan(p+b)= tanb ; cotga=cotg(p+b)=cotgb.
|
Riportiamo i valori 0 della cotangente a p/2 e 3p/2 e i valori +¥ e -¥ a 0, p e 2p. Otteniamo così la cotangendoide. Si noti che la curva assume gli stessi valori ogni p, per cui possiamo affermare che la funzione cotangente è di periodo p. Il grafico completo della cotangendoide si ottiene disegnando i valori degli angoli congruenti al primo giro.
|
Fonte: http://www.ettorevotta.it/TRIGONOMETRIA.doc
Autore del testo: non indicato nel documento di origine
Parola chiave google : Funzioni goniometriche tipo file : doc
Visita la nostra pagina principale
Funzioni goniometriche
Termini d' uso e privacy