Energy calculations
Energy calculations
The following texts are the property of their respective authors and we thank them for giving us the opportunity to share for free to students, teachers and users of the Web their texts will used only for illustrative educational and scientific purposes only.
The information of medicine and health contained in the site are of a general nature and purpose which is purely informative and for this reason may not replace in any case, the council of a doctor or a qualified entity legally to the profession.
Energy calculations
The branch of science that deals with the energy requirements of physical and chemical changes is called thermodynamics. This handout will cover various types of problems encountered in thermodynamics in a freshman chemistry course. The topics will include material found in both semesters (one year) of general chemistry.
There are many ways to look at energy. Let's look at some typical variables used to express energy and what they measure:
ΔE or ΔU measures the internal energy of a system –
i.e. the total energy of a system
q measures the heat of a system
w measures the work of a system
ΔH measures the enthalpy change of a system –
i.e. whether the process is exothermic or endothermic
ΔG measures the Gibb’s free energy change of a system –
i.e. whether a process is spontaneous or nonspontaneous
ΔS measures the entropy change of a system or surroundings
i.e. whether the randomness of the system or surroundings is increasing or decreasing
We will take each of these thermodynamic quantities in turn and examine them in more detail, as well as look at types of calculations involving these variables. In order to discuss these terms adequately, we need to define what is meant by a state function. A state function is a quantity whose value does not depend on the path used to measure the value. These quantities have upper case letters for symbols, such as, E, U, H, G, or S. Quantities, such as work, w, and heat, q, are not state functions. Their symbols use lower case letters. Also, the term “system” is defined as the part of the Universe being studied. It could be something like a chemical reaction or a phase change. The “surroundings” is everything else (the rest of the Universe).
Internal Energy
In most applications, internal energy is measured in terms of work and heat. The following equation relates internal energy, heat and work:
ΔE = q + w
This equation is often applied to the first law of thermodynamics. This law states that the energy of the universe remains constant, or energy can be both neither created nor destroyed, only changed from one form of energy to another.
The sign of q, heat, or work, w, indicates the direction of the flow of energy. The currently accepted sign convention is that if heat flows out the system to the surroundings, q is negative. If one were carrying out a reaction in a test tube, the test tube would feel warmer. If heat flows into the system from the surroundings, q is positive. If one were carrying out the reaction in a test tube, the test tube would feel colder. If the system does work on the surroundings, w is negative. This means that energy is flowing out of the system. If the surroundings do work on the system, w is positive. Energy is flowing into the system from the surroundings. The way to keep the signs straight is to relate them to what is happening to the system. Heat or energy flowing out of the system is negative; heat or energy flowing into the system is positive. Unfortunately, some areas of science choose to follow the opposite sign convention. It is important to note in a text which sign convention is used.
Let's look at a problem involving internal energy, heat and work. Suppose we have a process in which 3.4 kJ of heat flows out of the system while 4.8 kJ of work is done by the system on the surroundings. What is the internal energy?
Applying the equation, ΔE = q + w, one may calculate the internal energy:
ΔE = q + w = -3.4 kJ + (-4.8 kJ) = -8.2 kJ
Note the use of appropriate signs for heat and work. Overall, energy has flowed out of the system to the surroundings by -8.2 kJ.
There is another way in which work may be calculated, particularly when one is dealing with a gas phase system. The system consists of the gas and its container. Since gases may be expanded or compressed, work may be related by the pressure of the gas and the change in volume of the gas:
w = -PΔV
The change in volume, ΔV is always calculated as the final volume of the gas less the initial volume of the gas:
ΔV = Vfinal - Vinitial
To expand a gas, the volume of the gas is increased (ΔV is positive). The gas (part of the system) has to do work on the surroundings, and thus the work must be negative. Similarly, to compress a gas, the volume of the gas is decreased ΔV is negative). The surroundings must do work on the system, and thus the work must be positive.
Enthalpy
Heat of Formation
Enthalpy may be measured and calculated in many ways. We'll look at "theoretical" ways of calculating enthalpy, first, and then at some experimental methods.
One of the ways enthalpy may be calculated from theoretical data is from a table of the standard heat of formation, ΔHfo, of a substance. The standard heat of formation is defined as the enthalpy change taking place when a substance is formed from the elements in their standard states. Standard state, in thermodynamics is 1 atmosphere pressure and a temperature of 25 oC (298 K). Using the tabulated data found in any general chemistry textbook or other references, one may calculate the standard heat of reaction , ΔHrxno, by the following equation:
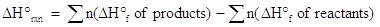
where n represents the moles of each reactant or product as found in the balanced chemical equation. The Greek letter, Σ , means one takes the sum of the variables which follow. When choosing ΔHfo values from a table, make sure you choose the value corresponding to the appropriate state of matter (solid, liquid, aqueous, gas). Also, note that the standard heat of formation for an element in its standard state always has a value of 0 kJ/mol.
Let's look at a problem in which the heat of reaction is calculated from the heats of formation. Suppose you are given the following balanced chemical equation and were asked to find the heat of reaction and determine whether the process is exothermic or endothermic:
 16 H2S(g) + 8 SO2(g) 16 H2O(l) + 3 S8(s)
16 H2S(g) + 8 SO2(g) 16 H2O(l) + 3 S8(s)
From a table of thermodynamic quantities, one can gather the appropriate values for the heats of formation of each the components in the reaction, and set up the equation to calculate the heat of reaction:
ΔHrxno = [16 mol(ΔHfo of H2O(l)) + 3 mol(ΔHfo of S8(s))] -
[16 mol(ΔHfo of H2S(g)) + 8 mol(ΔHfo of of SO2(g))]
ΔHrxno = [16 mol(-285.8 kJ/mol) + 3 mol(0 kJ/mol)] -
[16 mol(-20.2 kJ/mol) + 8 mol(-296.8 kJ/mol)]
ΔHrxno = [-4573 kJ + 0 kJ] - [-323 kJ + (-2374 kJ)]
ΔHrxno = -4573 kJ + 323 kJ + 2374 kJ
ΔHrxno = -1876 kJ
Since ΔHrxno is negative, the reaction is an exothermic process. Heat is released by the system to the surroundings. This particular reaction commonly occurs in the vents of volcanos, and deposits sulfur at the entrance of the vents. We will use this reaction to discuss other thermodynamic quantities, as well, throughout the handout.
Hess' Law
Hess' Law takes advantage of the fact that enthalpy is a state function. Recall that a state function depends only on initial and final states; it does not depend on the path one takes to go from one state to another. With Hess' Law, if an alternative means is found to calculate enthalpy, i.e., a series of reactions whose enthalpies are known, and the overall reaction gives the reaction sought, the sum of the enthalpies of those is the enthalpy of the sought reaction.
Let's look at an application of Hess' Law. Suppose we want to determine the enthalpy of reaction for the reaction:
 2 N2(g) + 5 O2(g) 2 N2O5(g) ΔH = ?
2 N2(g) + 5 O2(g) 2 N2O5(g) ΔH = ?
from the following heats of reaction:
 H = -571.7 kJ
H = -571.7 kJ
 H = -92 kJ
H = -92 kJ
 H = -348.2 kJ
H = -348.2 kJ
The goal is to manipulate the above equations in such a way that the overall equation sums to the equation sought. First, we have to decide the equation to start with. One usually looks at the compounds in the equation sought, and tries to find each of the compounds in one of the given equations. Nitrogen, N2 , is found only in equation (3), so we could start with this equation. Oxygen, O2, is found in both equations (1) and (3), so that is not a good compound with which to begin solving the problem. Dinitrogen pentoxide, N2O5 , is found only in equation (2), so we could also start with equation (3).
Arbitrarily, let's chose nitrogen and equation (3) and see what else we have to do this equation. Equation (3) is written containing only one mole of nitrogen as a reactant, and in the equation we seek, two moles of nitrogen, as a reactant are needed. Since nitrogen is a reactant in both instances, we do not need to reverse the equation, however, we do need to multiply equation (3) by two in order to obtain the required two moles of nitrogen. Whatever is done to manipulate the chemical equation is also applied to the heat of reaction; thus, we also multiply the given heat of reaction by two:
 2 x Eqn(3): 2 N2(g) + 6 O2(g) + 2 H2O(g) 4 HNO3(l) ΔH = 2(-348.7 kJ)
2 x Eqn(3): 2 N2(g) + 6 O2(g) + 2 H2O(g) 4 HNO3(l) ΔH = 2(-348.7 kJ)
= -696.4 kJ
Next, let's introduce dinitrogen pentoxide into the problem, since only equation (2) contained the compound. In the equation sought, N2O5 appears as two moles of product. In equation (2), N2O5 appears as one mole of reactant. We must reverse the equation and multiply by 2. This means we will also change the sign of the heat of reaction, and multiply it by two:
 -2 x Eqn(2): 4 HNO3(l) 2 N2O5(g) + 2 H2O(l) ΔH = -2(-92 kJ)
-2 x Eqn(2): 4 HNO3(l) 2 N2O5(g) + 2 H2O(l) ΔH = -2(-92 kJ)
= +184 kJ
At this point, let's look at the two equations generated. We see that the four moles of nitric acid will cancel. This is "convenient" since this compound is not found in the sought equation.
 2 x Eqn(3): 2 N2(g) + 6 O2(g) + 2 H2O(g)
2 x Eqn(3): 2 N2(g) + 6 O2(g) + 2 H2O(g) 4 HNO3(l) ΔH = 2(-348.7 kJ)
= -696.4 kJ
 -2 x Eqn(2):
-2 x Eqn(2): 4 HNO3(l) 2 N2O5(g) + 2 H2O(l) ΔH = -2(-92 kJ)
= +184 kJ
We also need to cancel two moles of H2 , two moles of H2O, and one mole of O2. This is accomplished using equation (1) in reverse. Remember to reverse the sign for the heat of reaction:
5
 2 x Eqn(3): 2 N2(g) +
2 x Eqn(3): 2 N2(g) + 6 O2(g) + 2 H2O(g) 4 HNO3(l) ΔH = 2(-348.7 kJ)
= -696.4 kJ
 -2 x Eqn(2):
-2 x Eqn(2): 4 HNO3(l) 2 N2O5(g) + 2 H2O(l) ΔH = -2(-92 kJ)
= +184 kJ
 -1 x Eqn(1)
-1 x Eqn(1) 2 H2O(l) 2 H2(g) + O2(g) ΔH = -1(571.7 kJ)
= +571.1 kJ
Summing the chemical equations gives us the sought reaction. Summing the heats of reaction gives us the heat of reaction for the overall process:
2 N2(g) + 5 O2(g)  2 N2O5(g) ΔH = +59 kJ
2 N2O5(g) ΔH = +59 kJ
Calorimetry
The basic principle behind calorimetry centers around heat flow. Heat lost by the system would equal to the heat gained by the surroundings during an exothermic process. Conversely, heat gained by the system from the surroundings would equal to the heat lost by the surroundings in an endothermic process.
A physical property relating the ability of a substance to hold heat is called the heat capacity. Heat capacity is defined as the amount of heat energy required to raise a substance by one degree Celsius. Often the specific heat capacity is used in place of heat capacity. The specific heat capacity differs from heat capacity in that it relates the amount of heat energy required to raise one gram of a substance by one degree Celsius.
The equation which relates heat, mass, specific heat capacity and temperature is shown below:
q = mCΔT
where q = heat in Joules
m = mass in grams
C = specific heat capacity in Joules/g°C
ΔT = temperature change in °C
In a typical calorimetry experiment, a hot substance (defined as the system) is introduced to a cold substance (defined as the surroundings). The system and surroundings are allowed to reach equilibrium at some final temperature. Heat flows from the hotter substance to the cooler substance. The heat lost by the hot substance (the system) must equal the heat gained by the cooler substance (the surroundings).
Let's look at a typical calorimetry problem. To begin with, in the real world, no calorimeter is perfectly insulating to temperature. The calorimeter itself, as part of the surroundings, will absorb some heat. The simplest and cheapest calorimeter is a styrofoam cup. It is often used in introductory chemistry classes as a calorimeter. Although the temperature insulating properties of styrofoam cup are fairly good, the cup will absorb some heat. Thus, to obtain the most accurate result, the "coffee cup calorimeter" must be calibrated. This is often performed as an experiment in which hot water of known mass and temperature is poured into a coffee cup containing cool water of known mass and temperature. The combined water samples are allowed to equilibrate to a final maximum temperature.
Suppose 60.1 g of water at 97.6 oC is poured into a coffee cup calorimeter containing 50.3 g of water at 24.7 oC. The final temperature of the combined water samples reaches 62.8 oC. What is the calorimeter constant?
To begin this problem, let's consider the basic principle of calorimetry:
heat lost by the hot water = heat gained by the cool water + heat gained by the calorimeter
Next, let's show the mathematical equations corresponding to the premise described:
heat lost by the hot water = heat gained by the cool water + heat gained by the calorimeter
- mhotCwater(Tfinal - Tinti, hot) = mcool Cwater(Tfinal - Tinit, cool) + Kcal (Tfinal - Tinit, cool)
Notice the negative sign in front of the expression for the heat lost by the hot water. Recall that heat lost is negative. Substitute the proper masses and temperatures into the above expression. Note that since the cool water was contained in the cup, the initial temperature of the calorimeter and the cool water are the same. The specific heat capacity of water, Cwater , has a value of 4.184 J/goC.
-(60.1 g)(4.184 J/goC)(62.8 oC - 97.6 oC) = (50.3 g)(4.184 J/oC)(62.8 oC - 24.7 oC)
+ Kcal (62.8 oC - 24.7 oC)
Combining terms gives: 8.75 x 103 J = 8.02 x 103 J + Kcal (38.1 oC)
Solving for Kcal :
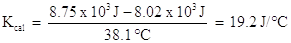
Now that the calorimeter has been calibrated, we can use it to determine the specific heat capacity of a metal. In this experiment, a known quantity of a metal is heated to a known temperature. The heat metal sample is dumped into a coffee cup calorimeter containing a known quantity of water at a known temperature. The temperature is allowed to equilibrate, and a final temperature is measured.
For instance, 28.2 g of an unknown metal is heated to 99.8 oC and placed into a coffee cup calorimeter containing 150.0 g of water at a temperature of 23.5 oC. The temperature of the water equilibrates at a final temperature of 25.0 oC. The calorimeter constant has been determined to be 19.2 J/oC. What is the specific heat capacity of the metal?
Once again set up the problem based on the heat flow:
heat lost by the hot metal = heat gained by the water + heat gained by the calorimeter
-(28.2 g)(Cmetal)(25.0 oC - 99.8 oC) = (150.0 g )(4.184 J/goC)(25.0 oC - 23.5 oC)
+ 19.2 J/oC(25.0 oC - 23.5 oC)
Combining terms gives:
2.11 x 103 goC (Cmetal ) = 9.4 x 102 J + 29 J
2.11 x 103 J (Cmetal ) = 969 J
Solving for specific heat capacity:
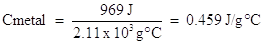
Metals tend to have low specific heat capacities. Water has a relatively high heat capacity. It is this property of water that helps control global temperatures. Temperature fluctuations during day and night would be much larger if the heat capacity of water was a lower value. This is evident in a desert where water is scarce. Daytime temperatures are very high, yet nighttime temperatures can drop to near freezing.
Entropy
Entropy, symbolized with an S, is a measure of the randomness or disorder in a system. The second law of thermodynamics states that for a spontaneous process, the entropy of the Universe will increase. Implicit in this statement is that to create order takes energy. Let's look at an example describing the second law of thermodynamics. To mimic a spontaneous process, suppose you had a sudden urge to take a piece of paper and tear it up into small pieces, and throw the pieces into the air. What would happen? The pieces of paper will randomly scatter about you. They certainly would not fly back together into the original piece of paper. You have just increased the entropy of the Universe. It did not take much energy to tear of the piece of paper and toss the pieces in the air. Now suppose you want to restore this piece of paper into its original form. How much energy would that take? First you have to expend some energy to go around the room and pick up the pieces of paper. The paper is still not restored to its original state. Next, you have to take the pieces of paper to a pulp mill and have the paper turned back into pulp and repressed into the original piece. These processes certainly took much more energy than the energy required to rip up the paper and toss it in the air.
One way to calculate entropy change is to use tabulated values for the entropy of formation. This calculation will look familiar since it follows the same format as the calculation of the enthalpy change from heats of formation. The equation is described below:
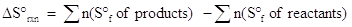
where n represents the moles of each reactant or product, as given in the balanced chemical equation.
Let's use this equation to solve an entropy problem. Suppose you wanted to know the entropy change for the same chemical equation we use to calculate the heat of reaction:
16 H2S(g) + 8 SO2(g)  16 H2O(l) + 3 S8(s)
16 H2O(l) + 3 S8(s)
Set up the equation:
ΔSorxn = [(16 mol)(Sof of H2O(l)) + (3 mol)(Sof of S8(s))] -
[(16 mol)(Sof of H2S(g)) + (8 mol)(Sof of SO2(g))]
From a table of standard entropies of formation, substitute in the quantities for the standard entropies of formation:
ΔSorxn = [(16 mol)(69.91 J/mol-K) + (3 mol)(31.80 J/mol-K)] -
[(16 mol)(205.79 J/mol-K) + (8 mol)(161.92 J/mol-K)]
Collect terms, and make sure that the mathematical signs are accounted for:
ΔSorxn = 1118 J/K + 95.40 J/K - 3292.6 J/K - 1295.4 J/K
Solving for the entropy of reaction gives:
ΔSorxn = -3375 J/K
Qualitatively, ΔSo < 0 represents a decrease in entropy. A ΔSo > 0 represents an increase in entropy. Solids have low entropy. The particles forming the solid are packed in an orderly matrix in the crystal. Liquids are intermediate in entropy. Intermolecular forces hold the particles in the liquid together in a slightly organized fashion. Gases are high in entropy. The gas particles are randomly moving around in their container with very few particles actually arranged in any orderly fashion. If we look at the above reaction, we see that a solid and a liquid are produced from gaseous products. Thus, it is not surprising that the entropy of reaction has a negative value.
In the previous example, ΔSorxn is a measure of the entropy change of a system. The entropy change of the surroundings is related to the heat flow and the temperature, as shown by the equation below:
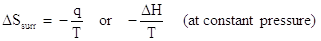
The negative sign in this equation accounts for the fact that the heat of the surroundings is opposite in sign to the heat of the system. From the previous example, we calculated that the enthalpy of reaction was -1876 kJ at standard temperature, 298 K. The entropy change of this system was calculated to be -3375 J/K (or 3.375 kJ/K). What is the entropy change of the surroundings?
Using the above equation:
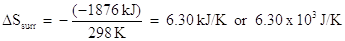
The result implies that the entropy of the surrounding increased. The total entropy change would be the sum of the entropy change of the system and the entropy change of the surroundings:
ΔStotal = ΔSsys + ΔSsurr
ΔStotal = -3.375 x 103 J/K + 6.30 x 103 J/K = 2.92 x 103 J/K
Overall, the entropy has increased. According to the second law of thermodynamics, this implies that the reaction we have been discussing is spontaneous. The best way to determine the spontaneity of a reaction is by looking at the next topic, Gibb's Free Energy.
Gibb's Free Energy
As mentioned, Gibb's free energy, ΔG, determines whether a reaction is spontaneous or nonspontaneous. If ΔG < 0, the reaction is spontaneous; if ΔG > 0, the reaction is nonspontaneous; if ΔG = 0, the reaction is at equilibrium. There are numerous ways to calculate Gibb's free energy. One of the methods will be analogous to previous methods discussed for enthalpy and entropy. The equation is shown below:
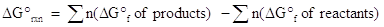
where n represents the moles of each product or reactant is given by the coefficient in the balanced chemical equation. As with enthalpy, you will find that the standard Gibb's free energy of formation of elements in their standard states is 0 kJ/mol.
Let's determine the change in the Gibb's free energy for the reaction we have discussed throughout the handout:
16 H2S(g) + 8 SO2(g)  16 H2O(l) + 3 S8(s)
16 H2O(l) + 3 S8(s)
Set up the equation:
ΔGorxn = [(16 mol)(Δ Gof of H2O(l)) + (3 mol)(Δ Gof of S8(s))] -
[(16 mol)(Δ Gof of H2S(g)) - (8 mol)(Δ Gof of SO2(g))]
From tabulated data, substitute for the Gibb's free energies:
ΔGorxn = [(16 mol)(-237.13 kJ/mol) + (3 mol)(0 kJ/mol)] -
[(16 mol)(-33.56 kJ/mol) + (8 mol)(-300.19 kJ/mol)]
Combine terms, paying careful attention to the mathematical signs:
ΔGorxn = -3794.1 kJ + 0 kJ + 537.0 kJ + 2401.5 kJ
ΔGorxn = -855.6 kJ
As predicted, the reaction is spontaneous, since ΔGorxn <0.
There is an alternative means for calculating ΔGorxn in which the Gibb's free energy is related to the enthalpy, entropy and temperature. If these values are known, then Gibb's free energy may be calculated by:
ΔGo = ΔHo - T ΔSo
From previous calculations, we have determined that the enthalpy change was -1876 kJ, the entropy change was -4.065 kJ/K, and the temperature has a value of 298 K (standard temperature). Notice that is important to make sure the units are consistent, so entropy, which is often expressed in units of J/K has been converted to kJ/K. Substituting these quantities into the above equation gives:
ΔGo = -1876 kJ - (298 K)(-3.375 kJ/K) = -870.2 kJ
This answer agrees reasonably well with the result from the calculation from the Gibb's free energies of formation.
Finally, there are two other equations to calculate  Go which are often encountered in an introductory level chemistry course. The first of these equations is:
Go which are often encountered in an introductory level chemistry course. The first of these equations is:
ΔGo = -RTln K or ΔGo = -2.303RTlog K
where R is the ideal gas law constant, 8.314 J/mol-K, T is temperature in kelvin, and K is the equilibrium constant for the chemical equilibrium taking place.
The second equation is:
ΔGo = -nFEo
where n represents the moles of electrons transfered in an electrochemical process, F is Faraday's constant, 96,485 C/mol, and Eo is the standard potential for an electrochemical cell. Calculation of the Gibb's free energy from these equations involves substitution of the appropriate quantities into the equation.
© Copyright, 2001, L. Ladon. Permission is granted to use and duplicate these materials for non-profit educational use, under the following conditions: No changes or modifications will be made without written permission from the author. Copyright registration marks and author acknowledgement must be retained intact.
Source : http://pages.towson.edu/ladon/energy.doc
Web site link: http://pages.towson.edu/ladon
Google key word : Energy calculations file type : doc
Author : L. Ladon
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Energy calculations
If you want to quickly find the pages about a particular topic as Energy calculations use the following search engine:
Energy calculations
Please visit our home page
Larapedia.com Terms of service and privacy page