Ideal and real gas laws

The following texts are the property of their respective authors and we thank them for giving us the opportunity to share for free to students, teachers and users of the Web their texts will used only for illustrative educational and scientific purposes only.

The information of medicine and health contained in the site are of a general nature and purpose which is purely informative and for this reason may not replace in any case, the council of a doctor or a qualified entity legally to the profession.

Ideal and real gas laws

IDEAL AND REAL GAS LAWS

Gases, unlike solids and liquids have indefinite shape and indefinite volume. As a result, they are subject to pressure changes, volume changes and temperature changes. Real gas behavior is actually complex. For now, let's look at ideal Gases, since their behavior is simpler. By understanding ideal gas behavior, real gas behavior becomes more tangible.

How do we describe an ideal gas? An ideal gas has the following properties:

1. An ideal gas is considered to be a "point mass". A point mass is a particle so small, its mass is very nearly zero. This means an ideal gas particle has virtually no volume.

2. Collisions between ideal Gases are "elastic". This means that no attractive or repulsive forces are involved during collisions. Also, the kinetic energy of the gas molecules remains constant since theses interparticle forces are lacking.

Volume and temperature are by now familiar concepts. Pressure, however, may need some explanation. Pressure is defined as a force per area. When gas molecules collide with the sides of a container, they are exerting a force over that area of the container. This gives rise to the pressure inside the container.

Problems Dealing With The Ideal Gas Law

For a gas, pressure, volume, temperature and the moles of gas are all related by the following equation:

PV = nRT

where P = pressure in atmospheres

V = volume in liters

n = moles of gas

R = ideal gas law constant (a proportionality constant)

T = temperature in Kelvin

The ideal gas law constant, R, dictates the units of pressure, volume and temperature. The most common used value for R when dealing with gases is 0.0821 L^. atm/mol^. K. This unit requires that volume to be expressed in liters, pressure to be expressed in atmospheres, and temperature to be expressed in Kelvin. One thing to keep in mind is that temperature will always be expressed in the Kelvin scale when dealing with any of the gas laws.

Let's start looking at some of the types of questions you may encounter using the ideal gas law. In some problems, you will know four out of the five possible variables, and be asked to solve for the fifth variable. It is important to note that the pressure, volume, moles or temperature of the gas is not changed. When these variables are changed, a different type of problem is apparent, and we will shortly look at these types of problems.

Suppose you have 1.00 mol of a gas at 0^oC, occupying a container which is 500 mL in size. What is the pressure of this gas in atmospheres?

To solve this problem, consider that moles, temperature, volume and the ideal gas law constant, R, are known. Pressure is the only unknown variable. Recall that R will dictate the units. The temperature is given in Celsius. This must be converted to the Kelvin scale. To convert Celsius to Kelvin, add 273 to the Celsius temperature:

K = ^oC + 273 = 0^oC + 273 = 273 K

Also, the volume must be in liters, not milliliters. Convert as follows:

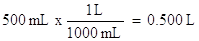
Now we are ready to insert the known values into the ideal gas law:

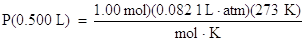
Solve for pressure by dividing both sides of the equation by the volume, 0.500 L:

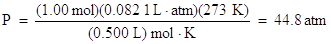
Notice how the units cancel to give atmospheres.

Next, let's find the volume of 2.50 mol of gas which is at 730 mm Hg of pressure, and at a temperature of 127 ^oC. As before, we need to convert temperature from Celsius to Kelvins:

K = 127 ^oC + 273 = 400 K

Additionally, we need to convert the pressure units of mm Hg to atmospheres. In one atmosphere of pressure, there are 760 mm Hg:

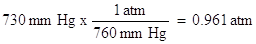
Remember, the reason for these conversions was to make the units consistent with the units of the ideal gas law constant, R.

Substitute the known values for pressure, moles, R, and temperature into the ideal gas law:

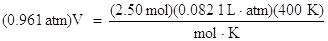
Divide both sides of the equation by the pressure, 0.961 atm, to solve for volume:

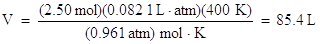
Again, notice how the units cancel to give volume units of liters.

Next, let's solve for the Celsius temperature of 0.600 mol of a gas at a pressure of 40000 torr, and a volume of 160 mL.

Unit conversions of pressure and volume must be done, first. We see here another pressure unit, torr. There are 760 torr in one atmosphere, and as one can see, the torr pressure unit is the same as the units of mm Hg.

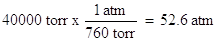
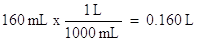
Once again, since the pressure and volume units are now consistent with the units of R, the values may be substituted into the ideal gas law:

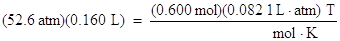
Divide both sides of the equation by the moles, 6.00 mol, and the ideal gas law constant, R, 0.0821 L^. atm/mol ^. K, to solve for temperature:

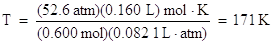
Notice how the units cancel to give temperature in K.

Convert the Kelvin temperature into Celsius:

^oC = K - 273 = 171 - 273 = -102 ^oC

Now let's find how many moles of gas are present when the gas is occupying a volume of 5.00 L at a pressure of 10.0 atmospheres and a temperature of 310 K. Substitute the pressure, volume, temperature and the gas constant, R, into the ideal gas law equation:

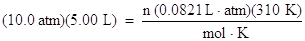
Divide both sides of the equation by the gas law constant, R, and the temperature to solve for n:

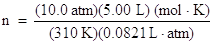
Other P,V,T, n Relationships (Empirical Gas Laws)

The ideal gas law may also be used to investigate the behavior of a gas when pressure, volume, the moles of gas and/or temperature are changed. These additional laws are often named after the scientist(s) who investigated these properties.

The relationship between pressure and volume while holding moles and temperature constant is called Boyle's Law. Let's derive this law. Assign subscripts to pressure and volume to indicate two different pressures and volumes:

P₁V₁ = nRT

P₂V₂ = nRT

Since both pressures and volumes are equal to nRT, they are equal to each other:

P₁V₁ = P₂V₂ = nRT (Boyle's Law)

Let's look at a problem dealing with Boyle's Law. Suppose you had gas in a 15.0 L container at 5.00 atmospheres pressure, and the volume is decreased to 0.500 L. What is the new pressure in the container?

To recognize that this is a Boyle's Law problem, make yourself a table of the known quantities and the unknown quantity.

P₁ = 5.00 atm P₂ = ?

V₁ = 15. 0 L V₂ = 0.500 L

Substitute the know variables into the equation for Boyle's Law. Make sure that the volume units are consistent. In this case, the volume units are both expressed in liters.

(5.00 atm)(15.0 L) = P2(0.500 L)

Solve for the new pressure, P₂, by dividing both sides of the equation by the new volume, 0.500 L:

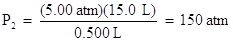
Note that pressure and volume are inversely proportional, so as volume decreases, the pressure increases.

The relationship between volume and temperature while holding moles and pressure constant is called Charles' Law. Let's derive this law from the ideal gas law. Assign subscripts to volume and temperature, and hold moles and pressure constant:

PV₁ = nRT₁

PV₂ = nRT₂

Collect terms. Bring the constants to one side of the equation and the variables to the other side of the equation. Divide both sides of each equation by pressure, P, and by the temperature term, T₁ in the first equation and T₂ in the second equation. This is Charles' Law:

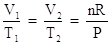
Let's look at a problem dealing with Charles' Law. Suppose you had 25.0 L of gas at 0 ^oC, and you raised the temperature to 100 ^oC. What is the new volume of the gas?

The first task is to immediately change the temperature values from Celsius to Kelvin. Remember, when dealing with any gas law, temperature values must be expressed in the absolute temperature scale (Kelvin scale). Why? Look at Charles' Law. If temperature were to remain in the Celsius scale, one would have to divide by 0 ^oC in the above problem. Division by 0 is undefined. Likewise, if one of the temperatures were negative, a negative volume would result, which is "impossible." By using the absolute temperature scale, negative temperature values do not exist, hence, negative or undefined volumes are not possible results.

T₁ = 0 ^oC + 273 = 273 K

T₂ = 100 ^oC + 273 = 373 K

Once again, to recognize that this is a Charles' Law problem, make a table of the known quantities and the unknown quantity:

V₁ = 25.0 L T₁ = 273 K

V₂ = ? T₂ = 373 K

Substitute the known temperatures and volume into the expression for Charles' Law:

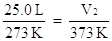
Solve for V₂ by multiplying both sides of the equation by T₂, 373 K:

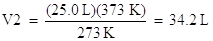
Note how volume and temperature are directly proportional. As the temperature increases, volume increases.

Now let's look at the case where pressure and temperature are varied and the moles and volume are held constant. This empirical gas law is called the Guy-Lussac Law. As before, give the terms that are varied, pressure and temperature, subscripts:

P₁V = nRT₁

P₂V = nRT₂

Collect terms. Divide each equation by their respective temperature term and each equation by the volume, V:

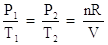
Let's use this law in a gas law problem. Suppose you have a gas at 30.0 atm pressure and 100 ^oC and the temperature is changed to 400 ^oC. What is the new pressure of the gas?

Again, the first step is to convert the temperatures from Celsius to Kelvin:

T₁ = 100 ^oC + 273 = 373 K

T₂ = 400 ^oC + 273 = 673 K

Set up a table of knowns and unknown:

P₁ = 30.0 atm T₁ = 373 K

P₂ = ? T₂ = 673 K

Substitute the known quantities into the Guy-Lussac equation:

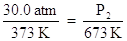
Solve the above expression for the pressure, P₂, by multiplying both sides of the equation by the temperature, 673 K:

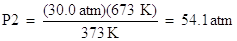
Notice that pressure and temperature are directly proportional. As the temperature increased, the pressure also increased.

The next empirical gas law we'll look at is called Avogadro's Law. This law deals with the relationship between the volume and moles of a gas at constant pressure and temperature. Let's derive this law from the ideal gas law. Give the moles and volume subscripts, since their conditions will change:

PV₁ = n₁RT

PV₂ = n₂RT

Collect terms. Divide each equation by pressure, P, and divide each equation by their respective mole term:

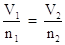
Let's use Avogadro's Law in a problem. Suppose you were given that 8.00 moles of a gas occupies a volume of 4.00L at a constant pressure and temperature. What volume of gas would 16.0 moles of this gas occupy at the same temperature and pressure?

Set up your table of knowns and unknown:

V₁ = 4.00 L n₁ = 8.00 mol

V₂ = ? n₂ = 16.0 mol

Substitute the known quantities into the equation for Avogadro's Law:

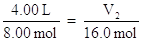
Solve the above equation for the volume, V₂, by multiplying both sides of the equation by 16.0 mol:

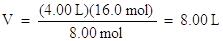
Notice how volume and moles are directly proportional. As the number of moles of gas increased, so did the volume of the gas.

The Combined Gas Law

What happens if none of the variables for a gas are constant (pressure, volume, temperature, and moles of the gas were changed)? The result would be the Combined Gas Law. Let's derive this law. Give pressure, volume, moles and temperature subscripts, since they are all changing:

P₁ V₁ = n₁RT₁

P₂V₂ = n₂RT₂

Collect terms. Divide each equation by their respective mole and temperature term:

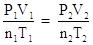
This equation is very useful since it contains any empirical gas law relationship you may need to come up with. If moles and temperature are held constant, then the above equation simplifies down to Boyle's Law. If pressure and moles are held constant, then the equation simplifies down to Charles' Law, etc. If only moles are held constant, then substitute the known pressure, volume and temperatures into the above equation and solve for the unknown quantity.

For instance, suppose you had a gas at 15.0 atm pressure, at a volume of 25.0 L and a temperature of 300 K. What would the volume of the gas be at standard temperature and pressure? Standard pressure is 1.00 atm and standard temperature is 0 ^oC (or 273 K)
.

Set up a table of knowns and unknown, as before:

P₁ = 15.0 atm P₂ = 1.00 atm

V₁ = 25.0 L V₂ = ?

T₁ = 300 K T₂ = 273 K

Substitute these variables into the combined gas law. Since the moles are unchanged, the mole terms have dropped out of the equation:

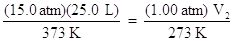
Solve the volume, V₂. Multiply both sides of the equation by 273 K and divide both sides of the equation by 1.00 atm:

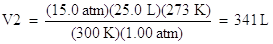
Other Equations Derived from the Ideal Gas Law

From the ideal gas law, PV = nRT, one can derive other useful expressions--ones that relate the molar mass and density of Gases to pressures and temperatures. This is often done just by substituting a different known expression for one of the variables in the ideal gas law. For instance, you know that the moles of a gas, n, can also be expressed as the mass of the gas in grams over the molar mass of that gas:

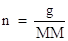
where MM = molar mass

g = grams of gas

n = moles of gas

Substitute this into the ideal gas law, and one obtains the equation:

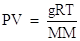
Multiplying both sides by the molar mass, MM, obtains:

(MM)PV = gRT

This equation is useful for determining the molar mass of a gas from experimental data, where the mass, pressure, volume and temperature of the gas is measured.

Now, let's divide both sides of the above expression by the volume, V:

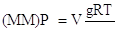
Since we know that g/V is density, D, let's substitute density in for g/V in the above equation:

(MM)P = DRT

This equation is useful for relating the pressure, density and temperature of a gas, in the same way as the other empirical gas laws we have encountered.

Real Gases

So far we have only considered the behavior of "ideal" Gases. How does a real gas differ from an ideal gas? Recall that an ideal gas is considered to be a point mass -- a particle so small that the volume of that particle is negligible. A real gas particle does have real volume. For an ideal gas, the collisions between gas particles was said to be "elastic" -- no attractive or repulsive forces exist, and thus, no energy is exchanged during collisions. For a real gas, collisions are non-elastic. There are a number of real gas laws. We will look at only one here, the van der Waal's equation:

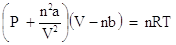
Notice how "corrections" are being made to the pressure term and the volume term. Since collisions of real Gases are non-elastic, the term n²a/V² is correcting for the interactions of these particles. The value of a is a constant, and must be experimentally determined for each gas. Since real gas particles have real volume, the nb term is correcting for the excluded volume. The value of b is a constant, and must be determined experimentally for each gas. The van der Waals constants, a and b for many gases have been tabulated in the CRC Handbook of Chemistry and Physics. Needless to say, they would be given to you if you are required to solve a problem using this equation. At this level, only pressure or temperature can be solved for easily. Solving for the volume is nontrivial and involves solving a cubic polynomial equation. Let's show how the van der Waals equation is rearranged to solve for pressure. Begin by dividing both sides of the equation by the volume term, V - nb:

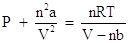
Next, subtract the interparticle interaction term, n²a/V² from both sides of the equation:

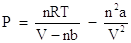
Using the real gas law, let's find the pressure of 2.00 moles of carbon dioxide gas at 298 K in a 5.00 L container. The van der Waals constants for carbon dioxide are: a = 3.592 L^2. atm/mol² and b = 0.04267 L/mol.

Substituting all of the variables into the appropriate terms of the equation, one obtains the pressure of :

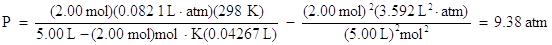
Compare this to the pressure calculated using the ideal gas law:

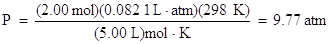
© Copyright, 2001, L. Ladon. Permission is granted to use and duplicate these materials for non-profit educational use, under the following conditions: No changes or modifications will be made without written permission from the author. Copyright registration marks and author acknowledgement must be retained intact.

Source : http://pages.towson.edu/ladon/gases.doc

Web site link: http://pages.towson.edu/ladon

Google key word : Ideal and real gas laws file type : doc

Author : L. Ladon

If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.