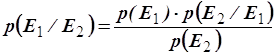Calcolo delle probabilità

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Calcolo delle probabilità

Definizioni

Il calcolo delle probabilità tende a rendere razionale il comportamento dell’uomo di fronte all’incertezza; di fatto viene utilizzato in tutte le situazioni in cui non sono prevedibili tutti i fattori osservabili e in quei casi in cui si debbono prendere decisioni in base ad ipotesi riguardanti eventi futuri.

Un evento casuale (detto anche evento aleatorio) è rappresentato da uno dei possibili risultati di un esperimento casuale. L’evento aleatorio può essere:

certo: quando il risultato è positivo e noto a priori (estrarre una pallina bianca da un un’urna contenente solo palline bianche);
impossibile: quando il risultato è nullo e noto a priori (estrarre una pallina nera da un un’urna contenente solo palline bianche);
possibile: quando il risultato non è noto a priori (estrarre una pallina nera da un un’urna contenente palline bianche e nere).

Nell’ultimo caso l’insieme dei risultati possibili si definisce spazio campionario e si indica con il simbolo W .

Lo spazio campionario si indica con:

W º (E₁; E₂;E₃;……;E_n)

essendo E_i il generico evento possibile ed n il numero di tali eventi.

A titolo di esempio:

l’estrazione di una pallina da un’urna con palline bianche e nere darebbe W º (B;N);

il lancio di due monete in successione darebbe W º (TT;TC;CT;CC);

l’estrazione di un bussolotto della tombola darebbe W º (1;2;3;4;…….;88;89;90);

il lancio di due dadi in successione darebbe W º (12;13;14;15;16;21;22;…….;64;65;66).

Due o più eventi si dicono incompatibili se il verificarsi di uno degli eventi esclude il verificarsi degli altri; si diranno compatibili nel caso contrario.

Due eventi incompatibili si dicono necessari se uno di essi deve verificarsi necessariamente.

Due o più eventi si dicono indipendenti se il verificarsi di uno non modifica il verificarsi dell’altro; si diranno dipendenti nel caso contrario.

Si chiama complementare dell’evento E quello corrispondente al non verificarsi dell’evento (si indica con Ē e si legge E negato o non E).

Ad esempio lanciando un dado, l’evento complementare all’uscita del numero 3 è dato dall’uscita dei numeri 1,2,4,5,6.

Si possono dare 4 diverse definizioni di probabilità:

soggettivista: la probabilità di un evento è il grado di aspettativa del verificarsi dell’evento (se diciamo che la probabilità di uscita della faccia testa nel lancio di una moneta è il 50% (1/2) gli attribuiamo un grado di fiducia maggiore di quello che attribuiremmo all’uscita del numero 3 nel lancio di un dado a cui diamo probabilità del 16,6% (1/6). Pertanto visto che la probabilità di un evento impossibile è zero e quella di un evento certo è 1, per il generico evento E si può scrivere:

0 ≤ Pr(E) ≤ 1

classica: la probabilità di un evento è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purché tutti i casi siano ugualmente possibili; a titolo di esempio:

l’uscita di doppia testa nel lancio di due monete in successione è pari ad 1/4 essendo TT uno dei 4 casi possibili (TT, TC, CT,CC);

l’uscita di una carta di bastoni da un mazzo di carte napoletane è pari ad 10/40 essendo 10 il numero dei bastoni presenti nel mazzo di 40 carte;

l’estrazione di una pallina bianca da un’urna contenente 5 palline rosse, 12 bianche e 8 nere è pari a 12/25 essendo 12 il numero dei casi favorevoli e 25 quelli possibili.

frequentista: la probabilità di un evento è il limite a cui tende la frequenza relativa di un evento (riscontrata in precedenti situazioni) al crescere del numero delle prove; si ricorda che la frequenza relativa è il rapporto tra il numero delle prove in cui si è manifestato l’evento e tutte le prove fatte.
assiomatica: la probabilità di un evento è quel numero reale p tale che:

0 ≤ p ≤ 1;

se l’evento è certo p(E)=1 e se l’evento è impossibile p(E)=0;

se due eventi E₁ ed E₂ sono incompatibili allora p(E₁ o E₂) = p(E₁) + p(E₂).

Teoremi

Quando si parla di eventi dipendenti debbono essere analizzate le probabilità subordinate, cioè la probabilità che il secondo evento si verifichi subordinatamente al verificarsi del primo evento; ad esempio se si volesse calcolare la probabilità di estrarre una carte di spade da un mazzo napoletano si avrebbe 10/40, qualora tuttavia la carta estratta fosse una seconda carta la sua probabilità risulterebbe diversa sapendo che la prima carta è stata il 3 di bastoni (probabilità=10/39) oppure il 5 di coppe (probabilità=10/39) oppure il 2 di spade (probabilità=9/39) e cosi via). La probabilità del verificarsi dell’evento E₂ subordinatamente all’evento E₁ si indica con p(E₂/ E₁). E’ evidente che nel caso di eventi indipendenti si avrebbe p(E₂/ E₂)= p(E₂)

I teoremi fondamentali sulle probabilità possono sintetizzarsi in:

probabilità composte: la probabilità del verificarsi di un evento che risulta dal concorso di due eventi è data dal prodotto delle probabilità del primo evento e del secondo subordinatamente al primo:

eventi dipendenti - p(E₁ e E₂) = p(E₁) * p(E₂/ E₁)

eventi indipendenti - p(E₁ e E₂) = p(E₁) * p(E₂)

probabilità totali: la probabilità che si verifichi uno dei due eventi E₁ o E₂ è data dalla somma delle probabilità dei due eventi diminuita della probabilità che si verifichino entrambi:

eventi compatibili - p(E₁ o E₂) = p(E₁) + p(E₂) - p(E₁ e E₂)

eventi incompatibili - p(E₁ o E₂) = p(E₁) + p(E₂) (la probabilità che si verifichino entrambi è ovviamente nulla).

Richiami di calcolo combinatorio

Per le applicazioni di calcolo delle probabilità è necessario conoscere alcune nozioni di calcolo combinatorio che possono essere sintetizzate nelle seguenti:

Permutazioni

Si dicono permutazioni di N elementi tutti quei gruppi che si possono formare con gli N elementi cambiando l’ordine degli elementi stessi; ad esempio avendo le prime tre lettere dell’alfabeto a, b, c, è possibile ottenere i seguenti gruppi: abc, acb, bac, bca, cab, cba.

Il numero dei gruppi che si possono formare risulta pari a

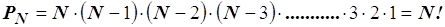
Il simbolo N! si legge N fattoriale e sta ad indicare il prodotto di N termini crescenti da 1 fino ad N.

Disposizioni

Si dicono disposizioni di N elementi di classe k tutti quei gruppi che si possono formare prendendo ogni volta k degli N elementi e cambiando ogni volta un elemento o l’ordine degli elementi stessi.

Le disposizioni possono essere:

senza ripetizione: quando ogni elemento deve comparire una sola volta in ciascun gruppo e risultano pari a (il numero dei termini del prodotto è pari a k):

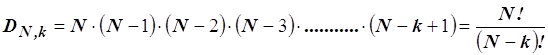
ad esempio avendo le prime quattro lettere dell’alfabeto a, b, c, d, prendendole a due a due è possibile ottenere i seguenti gruppi: ab, ac, ad, ba, bc, bd, ca, cb, cd, da, db, dc; il numero dei gruppi risulta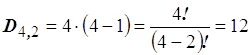

con ripetizione: quando ogni elemento può comparire più volte in ciascun gruppo e risultano pari a:

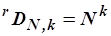
ad esempio avendo le prime quattro lettere dell’alfabeto a, b, c, d, prendendole a due a due è possibile ottenere i seguenti gruppi: aa, ab, ac, ad, ba, bb, bc, bd, ca, cb, cc, cd, da, db, dc, dd; il numero dei gruppi risulta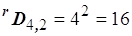

Combinazioni

Si dicono combinazioni di N elementi di classe k tutti quei gruppi che si possono formare prendendo ogni volta k degli N elementi e cambiando ogni volta un elemento e non l’ordine degli elementi stessi.

Le combinazioni possono essere:

senza ripetizione: quando ogni elemento deve comparire una sola volta in ciascun gruppo e risultano pari a:

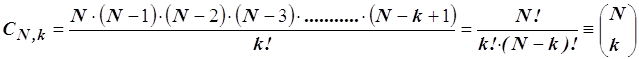
ad esempio avendo le prime cinque lettere dell’alfabeto a, b, c, d, e, prendendole a due a due è possibile ottenere i seguenti gruppi: ab, ac, ad, ae, bc, bd, be, cd, ce, de; il numero dei gruppi risulta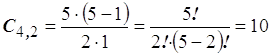

con ripetizione: quando ogni elemento può comparire più volte in ciascun gruppo e risultano pari a:

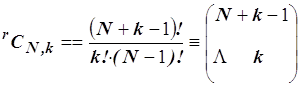
ad esempio avendo le prime cinque lettere dell’alfabeto a, b, c, d, e, prendendole a due a due è possibile ottenere i seguenti gruppi: aa, ab, ac, ad, ae, bb, bc, bd, be, cc, cd, ce, dd, de, ee; il numero dei gruppi risulta

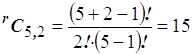
Legge empirica del caso

Sottoponendo un evento con probabilità p(E) ad una serie n di prove indipendenti ed effettuate nelle medesime condizioni, questo presenterà una frequenza assoluta k (numero delle volte in cui si è manifestato l’evento) ed una frequenza relativa f=k/n.

La legge empirica del caso, denominata anche legge dei grandi numeri, afferma che al crescere del numero delle prove la frequenza relativa f tende alla probabilità p(E); si deve precisare che la legge è molto generica: non vengono precisati i concetti di crescita del numero delle prove che non è comunque quella del limite nel senso di analisi matematica ed inoltre molto spesso è impossibile sottoporre un evento ad un numero molto grande di prove (basta pensare ad un esperimento scientifico).

In ogni modo, nei casi in cui la quantità delle informazioni è molto elevata, il fenomeno è assimilabile ai giochi d’azzardo (lancio di una moneta, estrazione di una carta) e quindi l’approccio frequentista può coincidere con quello soggettivista.

Teorema di Bayes

Riprendiamo il teorema delle probabilità composte ed il concetto delle probabilità subordinate e quindi quello di eventi dipendenti; per il teorema sugli eventi dipendenti si può scrivere:

p(E₁ e E₂) = p(E₁) * p(E₂/ E₁) oppure p(E₂ e E₁) = p(E₂) * p(E₁/ E₂)

e visto che le due probabilità p(E₁ e E₂) e p(E₂ e E₁)sono uguali si può scrivere:

p(E₁) * p(E₂/ E₁) = p(E₂) * p(E₁/ E₂) da cui

Le diverse probabilità che appaiono nell’ultima relazione che rappresenta il teorema di Bayes possono essere interpretate come:

p(E₁/ E₂) probabilità a posteriori, cioè la probabilità che avendo osservato l’evento E₁questo sia stato generato dalla causa E₂;

p(E₁) probabilità a priori;

p(E₂)probabilità dell’evento E₂ indipendentemente dall’altro evento;

p(E₂/ E₁) verosimiglianza cioè la probabilità dell’evento E₂ subordinatamente all’evento E₁.

Il teorema di Bayes consente di utilizzare tutta una serie di informazioni, disponibili da altre indagini statistiche relative agli eventi interessati (ad esempio la probabilità a priori e la verosimiglianza) in modo da poter ottenere una serie di convinzioni tradotte in distribuzioni a priori di probabilità.

Teorema delle prove ripetute

Considerando un evento E, estrazione di una pallina da un’urna contenente palline bianche e nere, con probabilità p e probabilità contraria q (pari a 1 – p), se si eseguono n estrazioni reinserendo ogni volta la pallina nell’urna, si vuole calcolare la probabilità che si presentino h palline bianche. La probabilità di estrarre le prime h palline bianche e le successive nere è data da (teorema delle probabilità composte):

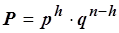
Considerando tutti i modi possibile di uscita nelle n prove (cioè alternando uscite bianche e nere) delle h palline bianche (combinazioni senza ripetizione di n elementi di classe h) si avrà che la probabilità cercata è pari a:

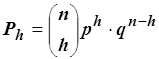
Fonte: estratto per uso didattico da http://www.sociologia.uniroma1.it/users/studenti/Appunti/Appunti%20Statistica/Appunti_Corso_Intensivo_Statistica.doc

Autore del testo:

Corso di Statistica
Prof.ssa Mary Fraire
Docente: Bruno Delle Donne

Calcolo delle probabilità