Statistica la distribuzione normale

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Statistica la distribuzione normale

La distribuzione normale

Nello studio delle distribuzioni statistiche occupa un posto di primo piano la determinazione della media e dello scarto quadratico medio non soltanto perché questi valori consentono di approfondire il fenomeno in oggetto, ma anche perché sono parametri utili nel confronto di distribuzioni diverse tra loro.
Quando si rappresentano graficamente i dati raccolti in un’indagine statistica che riguarda sia fenomeni sociali che naturali, ci si aspetta di ottenere una distribuzione normale o "a campana".
Essa ha la caratteristica di presentare un’alta densità di valori al centro e una bassa densità alle due estremità destra e sinistra, il che vuol dire che la maggior parte delle frequenze si distribuisce verso il centro.
La curva normale teorica è una curva simmetrica con asse di simmetria verticale coincidente con il valore della moda o norma, della media e della mediana della distribuzione. La simmetria della curva comporta che le osservazioni equidistanti dal massimo centrale hanno la stessa frequenza.
Le curve normali possono essere più "larghe" o più "strette" intorno all’asse di simmetria, a seconda del valore della deviazione standard; il valore di 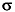, infatti, contribuisce a dare alla distribuzione la sua forma "a campana".
Si chiama curtosi la proprietà della curva di essere più o meno appiattita. Nella figura sono rappresentate una curva molto alta, detta leptocurtica, una molto bassa, detta platicurtica e la distribuzione normale che è detta mesocurtica.

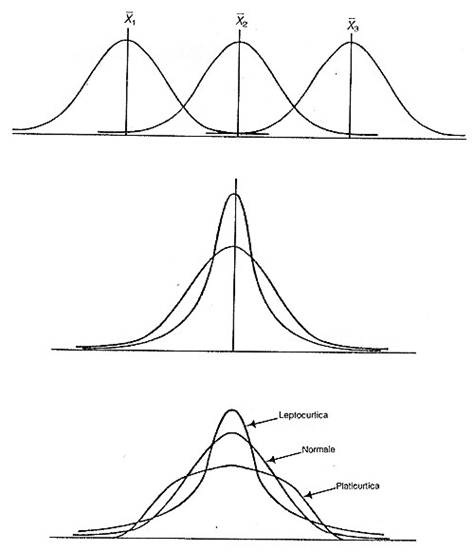
In alcuni casi la curva empirica presenta una asimmetria, cioè è deformata verso destra o sinistra. In questo tipo di curve, frequentemente presenti nella ricerca, occorre ricavarsi e analizzare le differenze tra i valori di media, moda e mediana e osservare se c’è dispersione dei dati verso le due code, che sono le estremità destra e sinistra della distribuzione.
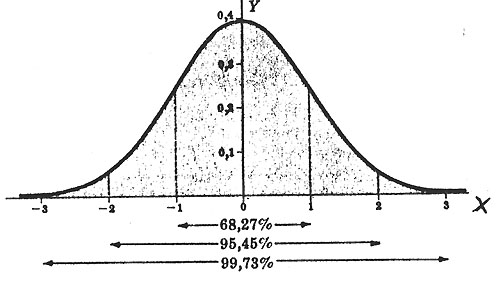
La curva normale teorica viene rappresentata nel piano cartesiano ponendo la media Xm = 0 e la deviazione standard 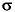= 1; in tal modo l’asse di simmetria coincide con l’asse Y.
Questo tipo di rappresentazione è molto utile perché consente di determinare in quale zona della curva si trovano le percentuali dei casi studiati.
Dopo aver stabilito che l’intera curva rappresenta il 100% dei casi, si suddivide l’asse orizzontale X in unità uguali a +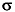= 1), circa il 95% dei casi tra -2 e +2 e il 99% è compreso tra -3 e +3, come mostra la figura.

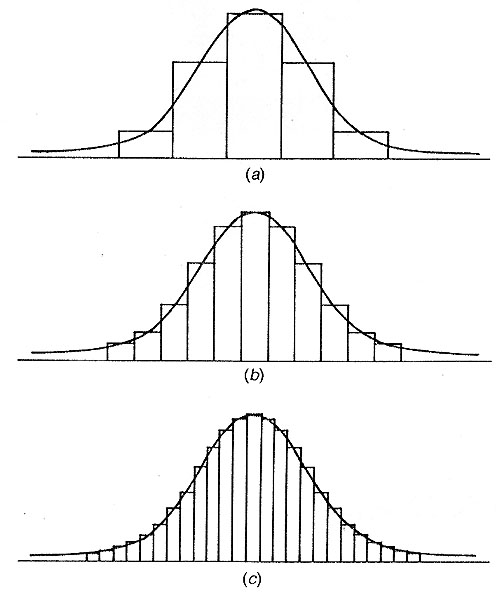
Nella pratica, quando si effettua un’indagine statistica su un fenomeno, si è soliti rappresentare i dati utilizzando un istogramma. A partire dall’istogramma si può disegnare il poligono di frequenze mediante una linea spezzata che congiunge le altezze dei rettangoli di un istogramma. Se la linea spezzata viene "arrotondata" e disegnata come una curva, può essere confrontata, ad esempio, con la curva normale.
Se si aumenta il numero delle persone intervistate, dunque, si ottiene un poligono di frequenze la cui forma è sempre più prossima a quella di una campana e, aumentando sempre più il numero degli intervistati, il poligono diventa una curva "normale" o di Gauss (ciò è dovuto alla casualità).
La caratteristica forma a campana della curva di Gauss indica che esiste un valore centrale, il valore medio, che rappresenta anche il valore più probabile.
Quando si afferma, ad esempio, che l'altezza media degli italiani è 1,70m, si può intendere che, scegliendo a caso un italiano e misurandone l'altezza, la probabilità che essa sia 1,70m è maggiore di tutte le altre. Intorno al valore più probabile sono distribuiti, con regolarità e simmetria, valori di probabilità via via decrescenti, nel senso che, a mano a mano che un valore si allontana dal valor medio, diventa sempre più piccola la sua probabilità.

Statistica la distribuzione normale