Statistica indici di dispersione media moda e mediana

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Statistica indici di dispersione media moda e mediana

Indici di dispersione - Media, moda e mediana

In un’indagine statistica, dopo aver tabulato e rappresentato graficamente i dati relativi ad un fenomeno, occorre sintetizzare la molteplicità di informazioni raccolte, analizzarle ed effettuare dei confronti con fenomeni analoghi. Il primo passo che si compie è, solitamente, l’individuazione dei valori medi statistici, in quanto essi hanno la caratteristica di rappresentare tutto l’insieme dei dati e di essere compresi tra il più piccolo ed il più grande dei valori raccolti.
Esistono vari tipi di medie e quelle più utilizzate sono la media aritmetica, la moda e la mediana. Esse hanno delle caratteristiche diverse tra cui la più evidente è che la media aritmetica è una media di calcolo mentre la moda e la mediana sono medie di posizione, come si vedrà mediante opportune esemplificazioni.

- Media aritmetica
In un insieme di dati statistici si dice media aritmetica semplice il numero ottenuto addizionando tutti i dati e dividendo tale somma per il numero dei dati.
Siano x1, x2,..., xn gli n valori assunti da una variabile statistica.
La media aritmetica semplice è il numero che si ottiene addizionando tutti i dati e dividendo la somma per il numero dei dati

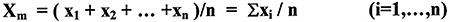
dove 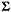(si legge sommatoria) è sigma, la lettera esse maiuscola dell’alfabeto greco.
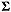indica la somma degli n valori assegnati; xi è uno dei dati e l’indice i sta appunto ad indicare che di x ve ne sono n e sono x1, x2,..., xn.
Se ad esempio uno studente A ha riportato i voti: 5, 7, 8, 9, la media aritmetica si calcola addizionando tutti i voti e dividendo il risultato per il numero dei voti che è 4:
Xm = (5 + 7 + 8 + 9)/ 4 = 29 / 4 = 7,25
Se i valori xi compaiono più volte cioè hanno frequenze fi diverse (il valore x1 ha frequenza f1, il valore x2 ha frequenza f2,...), la media aritmetica si chiama ponderata.

La media aritmetica ponderata è il numero che si ottiene addizionando i prodotti delle frequenze assolute fi per i corrispondenti valori xi e dividendo il risultato per la somma delle frequenze assolute

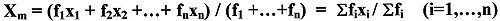
Se uno studente B ha riportato i voti:
6, 6, 6, 7, 7, 8, 9, 9,
per calcolare la loro media aritmetica si può utilizzare l’ultima formula, tenendo conto che il voto 6 ha frequenza 3 (f1x1=3*6=18), il voto 7 ha frequenza 2 (f2x2=2*7=14), il voto 8 ha frequenza 1, il voto 9 ha frequenza 2 (f4x4=2*9=18) e che i voti sono 8 (f1+f2+f3+f4 = 3+2+1+2 = 8).
Pertanto la media aritmetica ponderata sarà:
Xm = ( 3*6 + 2*7 + 1*8 + 2*9 )/(3 + 2 + 1 + 2) = (18 + 14 + 8 + 18)/8 = 58/8 = 7,25
I due studenti A e B, dunque, hanno lo stesso voto medio 7,25, pur essendo le rispettive distribuzioni di voti abbastanza diverse. In questo caso, per confrontare le valutazioni riportate dai due studenti, risulta utile calcolare anche gli scarti dalla media dei singoli dati all’interno di ciascuna distribuzione.
Si definisce scarto dalla media o deviazione la differenza tra un dato qualsiasi xi e la media Xm:

xi - Xm

Lo studente A ha riportato i voti 5, 7, 8, 9 con media aritmetica 7,25; gli scarti dalla media sono:

x1-Xm = 5-7,25 = -2,25	x2-Xm = 7-7,25 = -0,25
x3-Xm = 8-7,25 = 0,75	x4-Xm = 9-7,25 = 1,75

Lo studente B ha riportato i voti 6, 6, 6, 7, 7, 8, 9, 9 con media 7,25; gli scarti dalla media sono:

x1-Xm = 6-7,25 = -1,25	x2-Xm = 7-7,25 = -0,25
x3-Xm = 8-7,25 = 0,75	x4-Xm = 9-7,25 = 1,75

Dal confronto degli scarti risulta che la distribuzione dello studente A ha il primo valore che si allontana molto di più dalla media rispetto alla distribuzione dello studente B, quindi presenta una maggiore dispersione rispetto alla seconda. Ciò risulta palesemente se si considera che il primo voto dello studente A è 5.
Una delle proprietà dello scarto dalla media è la seguente: la somma di tutti gli scarti di una distribuzione è uguale a zero, essendo gli scarti positivi e negativi. Questa proprietà è facilmente verificabile addizionando, ad esempio, gli scarti dell’ultimo esempio e tenendo presenti le loro frequenze:
(-1,25*3-0,25*2+0,75+1,75*2) = (-3,75-0,5+0,75+3,5) = 0

- Media aritmetica di una distribuzione in classi
Il calcolo della media aritmetica di una distribuzione in classi richiede un procedimento più laborioso, in quanto è necessario trovare, preliminarmente, per ciascuna classe, il corrispondente valore centrale. Successivamente, si moltiplica ciascun valore centrale per la rispettiva frequenza assoluta; i prodotti ottenuti si addizionano ed il risultato si divide per il totale delle frequenze.
Il procedimento ora descritto è illustrato nella seguente tabella, che consente di trovare agevolmente l’altezza media di una distribuzione in classi di altezze:

Classe di altezze	Freq. assoluta fi	Valore centrale della classe	Prodotto fi*xi
151-155	4	(151+155)/2=153	4*153= 612
156-160	9	(156+160)/2=158	9*158= 1422
161-165	15	(161+165)/2=163	15*163= 2445
166-170	7	(166+170)/2=168	7*168= 1176
171-175	8	(171+175):2=173	8*173= 1384
176-180	3	(176+180)/2=178	3*178= 534
181-185	3	(181+185)/2=183	3*183= 549
186-190	1	(186+190)/2=188	1*188= 188
Totale	50		8310

La media aritmetica di una distribuzione in classi si calcola addizionando i prodotti delle frequenze assolute fi per i corrispondenti valori centrali xi di ciascuna classe e dividendo la somma ottenuta per il totale delle frequenze.
Xm = (4*153+9*158+15*163+7*168+8*173+3*178+3*183+1*188)/ 50 =
= (612+1422+2445+1176+1384+534+549+188)/ 50 =
= 8310/50 = 166,2 cm
è l’altezza media della distribuzione in classi di altezze assegnata.

- Moda o valore normale
In un insieme di dati statistici la moda è il dato o la classe di dati che ha la massima frequenza.
Esso è un valore che riveste grande importanza in quanto rappresenta un’osservazione concreta sul fenomeno che non deriva da calcoli aritmetici e non è influenzata dai dati molto alti o molto bassi. Nell’istogramma della distribuzione, la classe modale corrisponde alla base del rettangolo di altezza massima, quindi è facilmente individuabile.
Una distribuzione di dati statistici è detta unimodale se ha una sola moda: la seriazione di voti
5, 6, 6, 6, 7, 8, 8
ha moda 6, perché il voto 6 si ripete tre volte.
Una distribuzione è detta bimodale se ha due mode: la seriazione di voti
5, 5, 5, 6, 6, 7, 7, 7, 8
ha mode 5 e 7 perché entrambi i voti si ripetono tre volte.
Una distribuzione si dice plurimodale se ha più di due mode: la seriazione
6, 6, 7, 7, 8, 8, 9
ha tre mode perché i voti 6, 7 e 8 si ripetono due volte ciascuno.

- Mediana
In un insieme di dati statistici, ordinati in ordine crescente, la mediana è il valore che occupa la posizione centrale se i dati sono in numero dispari, altrimenti è la media aritmetica dei due numeri centrali se i dati sono in numero pari.
Se è assegnato un insieme dispari di valori
4, 5, 2, 8, 3
dopo averli ordinati dal più piccolo al più grande
2, 3, 4, 5, 8
si individua agevolmente la mediana 4, che è il valore centrale.
Se è assegnato un insieme pari di valori
5, 8, 12, 7, 6, 9
dopo averli ordinati in senso crescente
5, 6, 7, 8, 9, 12
si calcola la media aritmetica dei due valori centrali 7 e 8 :
(7 + 8)/2 = 15/2 = 7.5
che corrisponde alla mediana.

Nel caso di distribuzioni di frequenze con valori raggruppati in classi, la classe mediana si determina utilizzando il metodo delle frequenze cumulate e studiando opportunamente il relativo grafico (un esempio è riportato di seguito).
La mediana è una media di posizione e, come la moda, non è influenzata dai valori estremi. Essa ha la caratteristica di dividere in due parti uguali la successione di dati, pertanto si può definire come quel dato per il quale esistono tanti valori inferiori quanti superiori ad esso. Inoltre, la mediana divide l’istogramma della distribuzione in due aree uguali e, nell’ogiva delle frequenze cumulate essa corrisponde all’ascissa del punto la cui ordinata è 1/2 ovvero il 50%.
Nella tabella sono riportate le risposte errate ad un test raggruppate in classi, le corrispondenti frequenze assolute, cumulate e le relative percentuali.

Numero di risposte errate	Frequenza assoluta	Frequenza cumulata	Frequenza cumulata %
0-2	3	Fino a 126 : 3	7,5
3-5	5	Fino a 135 : 8	20
6-8	9	Fino a 144 : 17	42,5
9-11	12	Fino a 153 : 29	72,5
12-14	5	Fino a 162 : 34	85
15-17	4	Fino a 171 : 38	95
18-20	2	Fino a 180 : 40	100
Totale	40

Dalla tabella si ricavano il grafico delle frequenze assolute e l’ogiva delle frequenze cumulate espresse in percentuali, nei quali è indicato il valore della mediana.

Fonte: http://www.let.unicas.it/links/didattica/cartelli/master/Stasoc02.doc

Autore del testo: A. Cartelli

Parola chiave google : Statistica indici di dispersione media moda e mediana tipo file : doc

Statistica indici di dispersione media moda e mediana