Misura delle grandezze

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

GRANDEZZE FISICHE E UNITÀ DI MISURA

Che cos’è la Fisica?

La Fisica studia i fenomeni naturali e cerca di comprenderli trovando leggi, cioè relazioni, espresse in forma matematica, tra le grandezze fisiche.
Una qualsiasi affermazione riguardante i fenomeni naturali ha validità scientifica se soddisfa due requisiti fondamentali:
Deve essere oggettiva cioè interpretabile da chiunque allo stesso modo.
Deve essere verificabile, da chiunque e in qualsiasi momento.
Per questa ragione, le osservazioni relative a un dato fenomeno devono basarsi su caratteristiche dei corpi che possono essere misurate, alle quali cioè sia possibile associare dei valori numerici. Tali caratteristiche vengono definite grandezze fisiche.

L’importanza della misura in Fisica

“Ogni qualvolta vi è possibile misurare ed esprimere per mezzo di numeri l’argomento di cui state parlando, voi conoscete l’argomento di cui state parlando, voi conoscete effettivamente qualcosa; quando però ciò non vi è possibile o non ne siete capaci, scarsa e insoddisfacente è, da un punto di vista scientifico, la vostra conoscenza”.
Abbiamo riportato questa massima di W. Thomson (1824 – 1907), eminente fisico inglese, per precisare che il metodo operativo, cioè l’operazione di misura, è il fondamento dello studio scientifico.
In generale, si può affermare che il processo della conoscenza scientifica passa sempre attraverso la misurazione di grandezze fisiche, infatti, i dati relativi alle misure effettuate consentono sia la formulazione di leggi di tipo sperimentale su cui fondare poi dei modelli teorici, sia, viceversa, la verifica di determinati modelli teorici attraverso la ricerca sperimentale delle misure previste dal modello stesso. Anche le applicazioni pratiche, legate alle discipline tecnologiche, prevedono la misurazione di grandezze per giungere alla creazione di tutti gli oggetti di uso quotidiano o a macchinari che servono per produrre tali oggetti.

Grandezze fisiche e unità di misura

Per misurare qualcosa non possiamo usare i nostri sensi, sia perché a volte ci ingannano (basti pensare alle illusioni ottiche, che sono veri e propri errori di interpretazione delle sensazioni visive in cui cade il nostro cervello nel tentativo di valutare dimensioni e forme, o alla sensazione dello scorrere del tempo, che in taluni casi ci sembra non passare mai e in altri casi ci sembra che sia volato), sia perché comunque non ci forniscono una valutazione oggettiva ma soggettiva, cioè diversa da persona a persona. Se vogliamo studiare scientificamente la realtà, non possiamo allora limitarci alle informazioni che danno i nostri sensi, ma dobbiamo usare strumenti che ci forniscano dati il più possibile svincolati dall’esperienza soggettiva, e quindi una valutazione non soggettiva ma oggettiva, indipendente dall’osservatore.
Osserviamo però che non tutto si può misurare, perché non di tutto si può avere una valutazione oggettiva (es. bellezza, simpatia, ecc. sono caratteristiche soggettive). La Fisica si occupa solo di ciò che può essere misurato.
Chiamiamo grandezza fisica una qualsiasi caratteristica di un corpo o di un fenomeno che può essere misurata, alla quale cioè è possibile associare un numero. Osserviamo che per misurare una certa grandezza non occorre fare ragionamenti mentali astratti (tanto è vero che per alcune grandezze, come per esempio il tempo, non è possibile dare una vera e propria definizione, cioè non è ancora possibile rispondere in maniera precisa alla domanda su cosa sia questa grandezza) ma bisogna operare concretamente con strumenti reali; quindi per ogni grandezza fisica viene elaborato un determinato procedimento di misura. Si dice pertanto che le grandezze fisiche vengono definite operativamente nel senso che si definisce la grandezza anche o solamente attraverso la descrizione degli strumenti e della procedura che servono per misurarla. Per chiarire meglio questo concetto pensiamo alla seguente definizione che alcuni testi danno della massa di un oggetto: “la massa è la quantità di materia presente in un corpo”. Utilizzando quello che dice tale frase siamo capaci di misurare la massa di un certo oggetto? Certamente no. È invece tutt’altra cosa se si dice che la massa è quella grandezza fisica che si misura con una bilancia a bracci uguali (dando magari istruzioni pratiche precise su come costruire tale bilancia affinché funzioni nel miglior modo possibile) mettendo in un piattello della bilancia il corpo di cui si vuole conoscere la massa e sull’altro tante masse campioni uguali (per verificare che le masse campioni sono tutte uguali basterà metterne una su un piatto e le altre una alla volta sull’altro piatto e verificare che l’asta è sempre in equilibrio) finché l’asta della bilancia non è in equilibrio orizzontale. Per esempio se l’asta è in equilibrio con tre masse campioni da 1 kg posso dire che il mio corpo ha una massa di 3 kg. Quest’ultima definizione (che però necessiterebbe di ulteriori specificazioni sulle quali qui per semplicità non ci dilunghiamo) capite che è una definizione molto diversa dalla prima che risulta una definizione puramente astratta senza nessuna applicazione pratica perché non ci dice come operare se vogliamo misurare questa “quantità di materia” e se vogliamo sapere se un corpo ha più o meno “quantità di materia” di un altro.
Oltre alle caratteristiche, diciamo “astratte” che non si possono misurare (come per esempio la bellezza o la simpatia citate precedentemente), ci sono altre proprietà dei corpi molto più concrete ma che nonostante ciò non possono essere considerate grandezze fisiche come per esempio il sapore, perché non è stato possibile ancora elaborare per esse un procedimento di misura e quindi possono essere descritte solo qualitativamente. La scienza è riuscita a stabilire un lungo elenco di grandezze misurabili, ed è presumibile che la loro classificazione non sia conclusa. Ciò che non può essere misurato non può dirsi grandezza fisica, ma ciò non significa che sia qualcosa di scarsa importanza, significa soltanto che non può essere studiato con i metodi della fisica.
Una precisazione importante: non bisogna confondere la grandezza fisica relativa a un corpo con il corpo stesso; di uno stesso corpo si possono misurare più grandezze fisiche. Per esempio, nonostante nella vita quotidiana spesso si dica, in Fisica non ha senso la frase: “misuro un tavolo”; di un tavolo si possono misurare diverse grandezze fisiche quali la massa, la larghezza, l’altezza, ecc. Osserviamo infine che le grandezze fisiche non sono oggetti che si possono toccare con mano nel mondo reale, sono concetti astratti della nostra mente: in natura i fenomeni avvengono, e volendo descriverli scientificamente gli uomini hanno trovato utile inventare alcune caratteristiche misurabili (le grandezze fisiche, appunto) le quali quindi sono entità astratte che però sono in stretta relazione con i sistemi concreti che vogliamo studiare.
Le grandezze fisiche che studieremo inizialmente saranno la lunghezza, l’area, il volume, il tempo e la massa.

Che cosa significa misurare

Come primo esempio semplice ma intuitivo di misura, supponete di essere dentro una stanza i cui lati li chiameremo lato 1 e lato 2 (il terzo sarebbe il lato verticale che però a noi non interessa) e di voler sapere quante volte il lato 1 è maggiore del lato 2. Senza nessuno strumento a disposizione pensate allora di contare quanti palmi di mano sono contenuti nel lato 1 e nel lato 2, camminando lungo il bordo e riportando volta per volta il palmo lungo il bordo stesso. Se per esempio trovate che il lato 1 contiene 50 palmi mentre il lato 2 ne contiene 20, concludete che il lato 1 è lungo 2 volte e mezzo il lato 2. In questo procedimento ci sono le tre fasi tipiche del processo di misura: prima ho scelto la caratteristica dei lati della stanza da misurare, cioè la loro lunghezza (per vedere quante volte un lato è maggiore dell’altro non mi serve per esempio misurare altre grandezze fisiche come per esempio lo spessore di vernice che c’è su di essi o la loro direzione rispetto al nord geografico), poi ho scelto l’unità di misura (la lunghezza del mio palmo) e poi ho contato quante volte l’unità di misura è contenuta nella grandezza da misurare (in questo caso la lunghezza di ogni lato).
È bene precisare che le ultime due fasi non sempre vengono effettuate direttamente da una persona (come nell’esempio precedente); molto spesso quando si usa uno strumento per misurare una certa grandezza l’unità di misura è determinata dallo strumento stesso (se uso una bilancia tarata in grammi l’unità campione non la posso scegliere, sarà per forza il grammo, se uso un righello l’unità di misura sarà per forza il millimetro) e anche l’operazione di conteggio di quante volte l’unità di misura è contenuta nella grandezza molto spesso la esegue lo strumento, lasciando a noi solamente la lettura del risultato di tale conteggio.

Al termine di ogni processo di misura viene associata quindi a una caratteristica di un corpo (grandezza fisica) un ben preciso numero (risultato della misura) che sta a indicare quante volte l’unità di misura scelta (cioè una grandezza della stessa natura di quella che si vuole misurare e alla quale viene assegnato il valore unitario) è contenuta nella grandezza misurata. Per esempio, se la lunghezza di una sbarra è 3 m, significa che l’unità di misura “metro” è contenuta 3 volte nella lunghezza della sbarra; se la massa di un oggetto è 4,5 g, significa che l’unità di misura “grammo”è contenuta 4 volte e mezzo nella massa dell’oggetto.

Riassumendo, quando si vuole misurare una determinata grandezza fisica si compiono le seguenti operazioni:

Si sceglie quale caratteristica del corpo si vuole misurare (scelta della grandezza fisica)
Si sceglie una unità di misura adeguata (detta anche campione di misura o unità campione o semplicemente campione), cioè un altro oggetto con la stessa caratteristica, da utilizzare come unità campione
Si confronta l’unità di misura con la grandezza, ossia si conta quante volte l’unità campione è contenuta nella grandezza da misurare (cioè in qualche modo l’unità di misura viene “riportata” sulla grandezza da misurare).
Si determina l’incertezza associata al valore della misura (questo punto lo affronteremo più avanti)

Approfondimento:
Da quanto detto sopra capiamo che una grandezza fisica, per essere tale, deve poter permettere un confronto. Per esempio, perché la lunghezza è una grandezza fisica? Perché noi possiamo confrontare la lunghezza di due oggetti e stabilire quante volte uno dei due è più lungo dell’altro. Perché la bellezza non è una grandezza fisica? Perché non esiste nessun metodo per stabilire quante volte un oggetto è più bello di un altro. Inoltre, si deve avere un criterio per la definizione di somma (perché devo essere in grado di sommare l’unità di misura per se stessa fino a quando non arrivo all’uguaglianza con la grandezza in esame)

Due grandezze si dicono omogenee quando possono essere confrontate con la stessa unità di misura (esempio l’area di un tavolo e l’area di una stanza, la dimensione di un batterio e la distanza tra giove e il sole). Due grandezze fisiche che non possono essere confrontate con la stessa unità di misura si dicono non omogenee o eterogenee (per esempio la larghezza di un oggetto e la massa di un altro oggetto).

Grandezze fondamentali, grandezze derivate e sistemi di unità di misura

Supponiamo di aver misurato il bordo di un tavolo con un pezzo di spago e di aver visto che è lungo 3 volte il pezzo di spago. Se comunichiamo questo risultato a un nostro amico, egli non riuscirà a capire quanto è lungo il tavolo, a meno che non abbia, o non riesca a procurarsi, un pezzo di spago uguale al nostro. La comunicazione però resterebbe confinata tra noi e il nostro amico. Se vogliamo comunicare la lunghezza del nostro tavolo a chiunque, dobbiamo confrontarla con un’altra lunghezza campione che tutti possano procurarsi. Se ci mettiamo tutti d’accordo, e ci procuriamo tutti la stessa lunghezza campione con cui misurare, ciascuno di noi può comunicare a chiunque altro il valore della lunghezza di qualunque oggetto. Se non fosse così, sorgerebbero veramente dei problemi: immaginiamo per esempio di ordinare un pistone per un cilindro di diametro 52,5 mm; se quello che tu chiami “millimetro” non fosse uguale al millimetro del rivenditore, saresti davvero nei pasticci! In passato ogni piccola comunità definiva e quindi riconosceva solo le “sue” proprie unità di misura. Infatti la scelta dell’unità di misura è arbitraria, cioè siamo liberi di definire un’unità in qualunque modo ci faccia comodo. Si poteva anche avere il caso di uno stesso nome dato a una certa unità di misura da parte di due civiltà differenti che non aveva lo stesso identico valore: un esempio è lo stadio, che per gli Ateniesi era equivalente ai nostri 177 m mentre per gli Alessandrini ai nostri 185 m. Però, lo sviluppo delle società industriali con l’espandersi dei commerci e degli scambi fra terre sempre più lontane da un lato e dall’altro la necessità da parte della comunità scientifica di poter confrontare i risultati di esperimenti fatti in luoghi e tempi diversi, fecero sentire l’esigenza di una unificazione delle unità di misura, rispetto alla confusione allora imperante. Si è creato quindi un organismo internazionale (che attualmente è il BIPM: Bureau International des Poids et Mesures con sede a Sèvres, vicino a Parigi (sito internet www.bipm.fr), che si occupa proprio di definire le unità di misura delle varie grandezze fisiche a livello mondiale. In Italia, esistono due organismi che si occupano dei problemi legati alle unità di misura: l’Istituto Elettrotecnico Nazionale “Galileo Ferraris”, istituito nel 1935, con sede a Torino (sito internet www.ien.it), e l’Istituto di metrologia “Gustavo Colonnetti”, istituito nel 1968, anch’esso istituito a Torino.

Grandezze fondamentali e derivate

Le unità di misura si possono suddividere in due gruppi:
Unità di misura fondamentali: sono quelle unità di misura che vengono definite operativamente. Definire operativamente una unità di misura significa che per specificarla, cioè nel dire che cos’è quella unità, si deve far riferimento a un oggetto materiale esistente o devono essere indicate le istruzioni pratiche per costruirla, realizzarla concretamente. Ricordiamo che le grandezze fisiche sono caratteristiche misurabili dei corpi che abbiamo nella realtà concreta e pertanto dovranno essere misurate con unità di misura altrettanto concrete. Per capire meglio cosa significhi che una unità di misura deve essere definita operativamente, immaginiamo di aver stabilito un contatto radio con una civiltà extraterrestre che abita un pianeta lontano. Supponiamo che tale civiltà abbia raggiunto lo stesso livello di conoscenze fisiche di noi. Ovviamente è impossibile che essa usi le nostra stesse unità di misura. Pertanto, se gli dicessimo: “noi umani siamo alti in media 1,75 m” agli extraterrestri è come se non gli avessimo detto nulla, per loro la parola “metro” sarebbe semplicemente un nome. Ma se noi riuscissimo a fornirgli tutte le istruzioni necessarie affinché essi possano costruirsi concretamente nel loro pianeta un campione di lunghezza 1 m (vedremo che a questo scopo bisogna usare un fascio di luce), allora capirebbero cosa significa 1,75 m. Quelle grandezze fisiche che hanno come unità di misura un’unità di misura fondamentale si chiamano grandezze fondamentali.
Unità di misura derivate: Le grandezze utilizzate per descrivere tutti i fenomeni fisici sono un centinaio e potremmo in teoria per ognuna di esse definire un campione operativo di riferimento. Ma è facile capire che non è comodo avere questo gran numero di campioni; per ovviare a ciò ci viene in aiuto il fatto che le grandezze fisiche non sono tutte indipendenti l’una dall’altra, ma la maggior parte di esse sono legate da opportune relazioni matematiche (soprattutto moltiplicazioni e divisioni) ad altre grandezze. Per esempio, la grandezza fisica “velocità” si calcola dividendo una lunghezza per un tempo. Pertanto, non è necessario definire operativamente un campione per ciascuna grandezza fisica ma è sufficiente scegliere convenzionalmente un piccolo numero di unità fondamentali e ricavare da queste le unità di misura di tutte le altre grandezze. Quindi per una grandezza derivata non esiste nessun campione definito in modo operativo in quanto la sua unità di misura viene definita utilizzando le unità di misura di quelle grandezze fondamentali che sono legate a essa. Ritornando alla velocità, non è necessario inventare per essa una nuova unità di misura; poiché infatti la velocità, come vedremo, è il rapporto fra la distanza percorsa e il tempo impiegato, la sua unità di misura sarà il rapporto tra l’unità di misura della distanza (metro) e l’unità di misura del tempo (secondo), quindi il m/s. Da questo esempio notiamo anche che per le unità di misura derivate non è necessario progettare nemmeno uno strumento specifico per misurarle perché bastano gli strumenti di misura di quelle grandezze alle quali la grandezza in questione è legata (non c’è bisogno di costruire uno strumento specifico per misurare la velocità, perché bastano gli strumenti di misura della lunghezza e del tempo). Quelle grandezze fisiche che hanno come unità di misura un’unità di misura derivata si chiamano grandezze derivate.

Sistemi di unità di misura

L’insieme delle unità di misura fondamentali, mediante le quali può essere espressa ogni altra grandezza fisica, costituisce un sistema di unità di misura.

Un buon sistema di unità di misura per essere tale deve avere le seguenti caratteristiche:

I suoi campioni fondamentali devono essere il più possibile invarianti, cioè devono conservare inalterate le loro caratteristiche nel tempo. Questo ovviamente per far sì che la stessa misurazione dia sempre il medesimo risultato, se ripetuta. Per chiarire questo concetto facciamo un’analogia presa dalla vita quotidiana. Supponiamo che un muratore che sta costruendo una casa disponga di un metro molto sensibile alla temperatura, cioè che si allunga considerevolmente quando la temperatura esterna è più alta e diventa più corto quando la temperatura si abbassa. È ovvio che le misure delle stanze che costruirà non coincideranno con quelle stabilite dal progetto e si troverà in una bella confusione quando si accorgerà che misurando uno stesso lato di una stanza più volte ottiene valori diversi a seconda del giorno dell’orario nel quale esegue la misura. All’esigenza di rendere invarianti i campioni di misura di un sistema di unità, si può far fronte in due modi: si può realizzare il campione in un esemplare unico, conservandolo in condizioni ambientali opportune e accuratamente controllate (come si fa per il campione di chilogrammo) oppure si può dare al campione una definizione costituita da regole operative precise, non ambigue, che ne permettano la facile ed esatta riproduzione da parte di chiunque voglia disporne (come si fa per il campione di lunghezza per il quale si usa la luce).
I suoi campioni fondamentali devono essere facilmente riproducibili. Cioè deve essere relativamente facile eseguire copie standard del campione, in modo da creare i campioni secondari che si usano nell’industria, dai quali poi derivano gli strumenti che usiamo nella vita comune. Se il campione è definito da regole operative abbiamo detto sopra che tutti, attenendosi a tale regole, possono riprodurre il campione. Se il campione invece esiste in un esemplare unico, è indispensabile che se ne possano fare con facilità delle copie, il più possibile uguali, che possano servire da campioni secondari per l’uso corrente. Per esempio, per quanto riguarda la massa, il campione riconosciuto a livello internazionale è un cilindro di platino - iridio conservato presso l’Ufficio Internazionale di Pesi e Misure, che si trova vicino a Parigi. Campioni secondari ottenuti mediante il confronto con una bilancia a bracci uguali, sono stati inviati a laboratori specializzati in altri paesi e le masse di altri oggetti possono essere determinati pesandoli su bilance a bracci uguali insieme ai campioni secondari. I campioni secondari in possesso dei vari paesi vengono rimossi non più di una volta all’anno per tarare i campioni terziari che sono usati altrove. Molto raramente i campioni secondari vengono portati in Francia per riconfrontarli con il campione principale. In Italia la copia numero 62 del kilogrammo campione è conservata a Torino, presso l’Istituto di Metrologia Gustavo Colonnetti.
Le sue unità di misura fondamentali devono essere convenienti cioè devono essere pratiche e possibilmente comode da usare sia nella vita di tutti i giorni sia nella pratica scientifica. Ossia conviene, per quanto possibile, che l’unità venga scelta in modo tale che gli esemplari della grandezza fisica con cui si ha di solito a che fare risultino caratterizzati da numeri né tropo grandi né troppo piccoli, possibilmente dell’ordine dell’unità (quando ciò non è possibile, o interferisce con altre richieste più importanti, si rimedia facendo uso in pratica di multipli o sottomultipli convenienti del campione prescelto). Per esempio, il metro è un’unità a misura d’uomo. Infatti la nostra altezza e molti oggetti che incontriamo nella vita quotidiana sono dell’ordine del metro. Se fossimo piccoli come le formiche o grandi come le montagne, con ogni probabilità avremmo scelto una diversa unità per misurare le lunghezze. Una cosa da chiarire è questa: sono le unità di misura a dover essere convenienti (infatti l’unità “metro”, l’unità “secondo” e l’unità “chilogrammo” sono usate comunemente da tutti), ma non certo i campioni fondamentali, che vengono infatti realizzati con procedimenti molto sofisticati (basti pensare all’orologio atomico per realizzare il campione di secondo). Questo non perché gli scienziati vogliano tenere solo per loro i campioni, ma perché quello che interessa prima è la loro invariabilità, e poi si fa un grande sforzo per rendere facilmente accessibili a tutti coloro che ne hanno bisogno dei duplicati il più fedeli possibile ai campioni fondamentali.
Le sue grandezze fondamentali devono essere indipendenti fra loro e il loro numero deve essere il più piccolo possibile, ma nello stesso tempo il sistema deve risultare completo, cioè l’insieme delle grandezze fondamentali deve essere sufficiente a descrivere tutti i fenomeni fisici finora conosciuti.
Deve essere coerente, cioè le grandezze derivate devono ottenersi da quelle fondamentali tramite prodotti, quozienti e potenze senza alcun coefficiente numerico
Deve avere i multipli e i sottomultipli decimali

Il Sistema Internazionale: Il Sistema Internazionale (abbreviato S.I) è usato da tutta la comunità scientifica a partire dal 1960. Al Sistema Internazionale hanno formalmente aderito 48 nazioni. Ancora oggi esistono alcuni Paesi, come l’Inghilterra e gli Stati Uniti, che non si sono ancora uniformati totalmente al sistema decimale ed utilizzano unità di misura proprie e non universali, come quelle di lunghezza: pollice, piede, miglio; o quelle per il peso: libbra, oncia, ecc. L’unico Stato che non ha adottato ufficialmente il S.I. sono gli Stati Uniti d’America. In alcuni settori, inoltre, continuano ad essere usate ancora delle unità di misura anomale, come per esempio il carato (200 mg) per le pietre preziose o il barile per il petrolio. Oltre al S.I. ricordiamo che ci sono altri sistemi come il sistema inglese che è utilizzato nei paesi di lingua anglosassone ed in alcuni settori tecnologici (es. in idraulica). Sono espresse nel sistema inglese diametri di tubature (pollici – inch), filettature ecc. Occorre sottolineare che il sistema inglese è di natura non decimale (cosa significa lo vedremo più avanti). Un altro sistema è il cosiddetto sistema c.g.s. (che sta per “centimetro”, “grammo”, “secondo”). È un sistema tuttora molto utilizzato nelle discipline in cui vengono effettuate misurazioni di piccoli quantitativi di sostanze; sostituisce il centimetro al metro come unità di misura della lunghezza ed il grammo al kilogrammo per la massa.
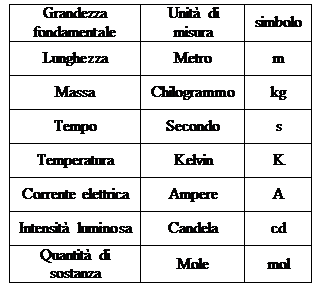
Ritornando al S.I., i suoi campioni sono definiti solo per sette grandezze fondamentali e per due grandezze supplementari. Tutte le altre grandezze fisiche sono derivate, cioè le loro unità di misura si ottengono da quelle delle grandezze fondamentali attraverso le relazioni matematiche che le definiscono. La scelta delle grandezze fondamentali è spesso dettata da motivazioni di carattere tecnico –pratico: per esempio, in passato la carica elettrica era considerata una grandezza fondamentale e l’intensità di corrente elettrica una grandezza derivata; ora i ruoli si sono invertiti perché è tecnicamente più semplice misurare una corrente elettrica. Le unità fondamentali del S.I. sono riportate nella tabella che segue. In essa sono scritte anche le definizioni delle unità di misura, per quanto a voi ora possano sembrare quasi tutte pressoché incomprensibili, un po’ per completezza di documentazione, e un po’ per darvi un’idea, seppur vaga, della complessità che comporta la definizione di un’unità di misura. Accanto alle definizioni abbiamo messo anche le date in cui sono state adottate.

GRANDEZZE E UNITà FONDAMENTALI DEL S.I.
GRANDEZZA	NOME DELL’UNITà di misura		SIMBOLO DELL’UNITà di misura	DEFINIZIONE
lunghezza	metro		m	il metro è lunghezza del tragitto percorso nel vuoto dalla luce in un intervallo di tempo pari alla frazione 1/299.792.458 di un secondo (1983)
massa	kilogrammo		kg	il kilogrammo è la massa del prototipo internazionale realizzato in platino iridio nel 1889 e conservato a Sevres dal B.I.P.M. (questa è l’unica unità basata su un campione materiale) (1901)
tempo	secondo		s	il secondo è l’intervallo di tempo che contiene 9.192.631.770 oscillazioni della radiazione emessa nella transizione tra i due livelli iperfini dello stato fondamentale dell’atomo di cesio 133 (1967)
intensità di corrente elettrica	Ampere		A	L’ampere è l’intensità di corrente elettrica che, mantenuta costante in due conduttori rettilinei, paralleli, di lunghezza infinita, di sezione circolare trascurabile e posti alla distanza di un metro l’uno dall’altro, nel vuoto, produce la forza di 2 · 107 N su ogni metro di lunghezza di ogni filo (1948)
temperatura	Kelvin		K	Il kelvin è la frazione 1/273,16 della temperatura termodinamica del punto triplo dell’acqua (1967)
intensità luminosa	candela		cd	la candela è l’intensità luminosa emessa, in una data direzione, da una sorgente monocromatica di frequenza 540 · 1012 Hz, e di intensità pari a 1/683 W/sr (1979)
quantità di sostanza	mole		mol	la mole è la quantità di sostanza di un sistema che contiene tante entità elementari quanti sono gli atomi contenuti in 0,012 kg di Carbonio 12. (1971) Le entità elementari devono essere specificate e possono essere atomi, ioni, elettroni, ecc., ovvero gruppi specificati di tali particelle
GRANDEZZE SUPPLEMENTARI DEL S.I.
angolo piano		radiante	rad	Il radiante è l’angolo piano al centro che intercetta su una circonferenza un arco lungo quanto il raggio
angolo solido		steradiante	sr	Lo steradiante è l’angolo solido al centro che intercetta su una sfera una calotta di superficie uguale a quella del quadrato costruito sul raggio

Osserviamo che il nome “supplementari” dato al radiante e allo steradiante deriva dal fatto che i metrologi sono incerti sulla loro natura, cioè se debbano considerarsi grandezze fondamentali o derivate. Infatti, ad esempio nello studio di un moto circolare, l’angolo espresso in radianti è utilizzato come una grandezza fondamentale, mentre se lo si considera come il rapporto fra arco e raggio diviene un’unità derivata
Osserviamo che con l’adozione della definizione di metro sopra riportata la velocità della luce nel vuoto è fissata e vale 1/299792458 secondi.

Facciamo notare che nel corso della storia le definizioni dei campioni non sono sempre state queste, perché si sono continuamente evolute. Si è avuto cioè che, per una certa grandezza fisica, una nuova definizione di campione ha soppiantato la vecchia, anche se la nuova definizione è stata scelta in modo da essere il più possibile in accordo con quella vecchia.

Inoltre, la scelta di quali grandezze fisiche debbano essere fondamentali è spesso dettata da motivazioni di carattere tecnico – pratico. Per esempio, in passato la carica elettrica era considerata fondamentale e di conseguenza l’intensità di corrente elettrica una grandezza derivata; ora i ruoli sono invertiti perché è tecnicamente più semplice misurare una corrente elettrica.
Come si vede dalla tabella sopra, tranne che per la massa, per le grandezze fondamentali si usano i campioni naturali, ossia si sfruttano fenomeni naturali (per il metro si sfrutta la luce, per il secondo si sfrutta il comportamento degli atomi di cesio, ecc). I campioni naturali, a differenza dei campioni materiali che sono quelli realizzati dall’uomo, non deteriorano nel tempo e sono accessibili a tutti, anche se tramite strumentazioni sofisticate. In sostanza, è la natura che custodisce il campione scelto a non un determinato ufficio, e pertanto esso può essere riprodotto in qualsiasi momento. Ricordiamo a questo proposito che la precedente definizione di metro come la lunghezza di quella sbarra di platino – iridio conservata presso Parigi era legata ad un campione materiale, e quindi più facilmente variabile nel tempo.

Infine, osserviamo che la temperatura, l’intensità luminose e la quantità di sostanza, non sono fondamentali nello stesso senso in cui lo sono la lunghezza, il tempo, la massa e la carica elettrica. Si verifica infatti che la temperatura può essere descritta come una misura dell’energia cinetica media delle molecole, la quale, a sua volta,, è descritta per mezzo delle grandezze lunghezza, tempo, massa. Analogamente, l’intensità luminosa può essere espressa in funzione delle grandezze energia, area e tempo, le quali di nuovo, si possono descrivere per mezzo delle grandezze lunghezza, tempo e massa.

Nella tabella seguente, invece, riportiamo alcune delle grandezze derivate più importanti del S.I. e alcune grandezze

ALCUNE GRANDEZZE DERIVATE DEL S.I.
Grandezza fisica	Simbolo della grandezza	Nome dell’unità di misura nel S.I.	Simbolo dell’unità S.I.	Equivalenza in termini di unità fondamentali S.I.
Area	A	Metro quadrato		m2
Volume	V			m3
Velocità	v			m · s–1
Accelerazione	a			m · s–2
Densità	ρ o d			kg · m–3
Potenza	P	Watt	W	J · s–1	= kg · m2 · s–3
Forza	F	Newton	N	kg · m · s–2
pressione, sollecitazione	p	Pascal	Pa	N · m–2	= kg · m-1 · s–2
energia, lavoro	E	Joule	J	N · m	= kg · m2 · s–2
carica elettrica	q	Coulomb	C	A · s

Nella tabella seguente riportiamo infine alcune di uso corrente che però non fanno parte del S.I.

Unità di misura di uso corrente NON FACENTI PARTE DEL S.I.
Nome della grandezza	Simbolo della grandezza	Nome dell’unità di misura	Simbolo dell’unità di misura
Temperatura	T	Celsius	°C
tempo	t	Minuto/ora/giorno	min / h / d
Capacità	V	Litro	L
Pressione	p	Bar, atmosfera	Bar, Atm
Massa	m	Quintale	q.le
Energia	E	Caloria	cal
Potenza	P	Cavallo vapore	cV

Fonte: http://www.webalice.it/paolocesaretti/appunti/unita_di_misura.doc

Sito web da visitare: http://www.webalice.it/paolocesaretti/

Autore del testo: non indicato nel documento di origine

LA MISURA DELLE GRANDEZZE

Qualsiasi ipotesi scientifica deve sempre basarsi su dei dati, e quindi qualsiasi ricerca scientifica deve partire da una fase di osservazione, finalizzata alla raccolta di dati (misure, descrizioni, rilevazioni, analisi, ecc.), che deve essere fatta nel modo più esatto, rigoroso e sistematico possibile. Molte scoperte scientifiche sono state rese possibili proprio dal fatto che lo scienziato che ne è stato l’autore non ha trascurato niente (Copernico e Mendel).
Per verificare le nostre capacità di osservare proviamo ad:

Elencare gli oggetti che si trovano sul banco, riportando per ognuno le caratteristiche che si ritengono importanti per descriverlo. Alcune caratteristiche (lunghezza) sono misurabili, altre ( ruvidità ) invece no.
Elencare i materiali che formano ciascuno degli oggetti. Alcuni corpi sono formati da un solo materiale, altri da due o più materiali. Alcuni materiali sono presenti in più corpi. Esistono proprietà caratteristiche dei corpi (lunghezza, peso, forma, ecc.), mentre altre sono caratteristiche dei materiali (colore, durezza, rigidità, ecc.). Anche i materiali possiedono caratteristiche misurabili ( peso specifico, durezza, ecc.) e caratteristiche non misurabili ( lucentezza).

Le caratteristiche misurabili hanno il vantaggio, grazie alla misura, di eliminare ogni possibile ambiguità e/o soggettività ( cosa significa essere “alto”, “caldo”, “pesante”, “bello”, ecc.).
Le proprietà misurabili sono dette grandezze fisiche.
Per misurare un oggetto dobbiamo scegliere una unità di misura, costituita da una qualità dello stesso tipo di quella in esame, il cui valore viene fissato pari a 1.
Misurare una grandezza vuol dire stabilire quante unità di misura sono contenute al suo interno.

La misura di una grandezza è sempre data da un valore numerico e da una unità di misura (es. m = 65 kg).
Per essere valida da un punto di vista scientifico una unità di misura deve:

Essere definita con molta precisione;
Essere uguale per tutti.
Possedere multipli e sottomultipli.

Misure lineari lombarde e lo rapporti col metro
Città lombarde e loro misure	Misure della città in metri	Metro in misura della città
Bergamo, braccio mercantile	0,659	1,517
Bergamo, braccio da fabbrica	0,531	1,881
Brescia, braccio mercantile da panno	0,674	1,483
Brescia, braccio da seta e tela	0,640	1,561
Braccio mercantile di Como, Cremona, Lodi, Pavia e Milano	0,594	1,680
Mantova, braccio mercantile	0,637	1,567
Sondrio, braccio lungo	0,671	1,488
Sondrio, braccio corto	0,530	1,884
Crema, braccio mercantile	0,670	1,402

Per risolvere tutti questi problemi è stato istituito il Sistema Internazionale delle Unità di Misura (SI), costituito dalle sette unità di misura delle sette grandezze fondamentali.
Tutte le altre grandezze fisiche, che si ottengono dalla composizione delle grandezze fondamentali, si definiscono invece grandezze derivate. Ne sono esempi la superficie (che si misura in m2 o la velocità, che si misura in m/s).
La notazione esponenziale
Ogni unità di misura deve possedere multipli e sottomultipli, che vengono utilizzati a seconda delle dimensioni degli oggetti da misurare, al fine di rendere più semplice la lettura ed i calcoli con le misure stesse. Multipli e sottomultipli variano secondo le potenze di 10 e sono rappresentate con
dei prefissi, secondo lo schema riportato nella tabella a lato. Per passare da un multiplo, o sottomultiplo, ad un altro è necessario fare delle equivalenze. Queste possono essere risolte tramite una proporzione oppure semplicemente ricordando che, per passare

100 = 1	10-1 = 1/10 = 0,1
101 = 10	10-2 = 1/100 = 0,01
102 = 100	10-3 = 1/1000 = 0,001

da una certa grandezza ad un’altra maggiore, la virgola deve essere spostata verso sinistra in base alla distanza tra le due unità di misura (ad esempio 5,0 m = 0,005 km); in modo analogo si sposta la virgola verso destra quando si passa ad una unità minore (ad esempio 5,0 m = 5000 mm). Quando i valori sono molto piccoli (vedi ad esempio il raggio dell’atomo di idrogeno, pari a 0,0000000529 mm), o molto grandi (come ad esempio la distanza Terra Sole, pari a 149 000 000 km), si vengono ad avere molti zeri, che complicano la lettura e le operazioni con tali numeri. Per ovviare a tali problemi si utilizza la notazione esponenziale, o scientifica, con la quale è possibile esprimere tali numeri attraverso le potenze di 10, eliminando così gli zeri e semplificando i calcoli. Ricordando le proprietà delle potenze riportate nella tabella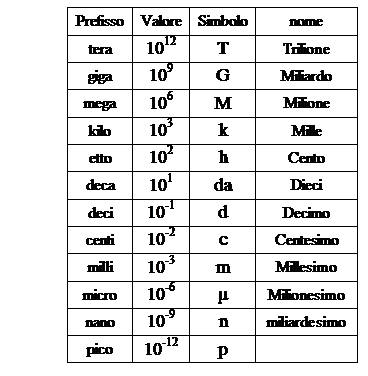 a fianco, i numeri prima citati diventano:
0,0000000529 = 529 • 10 –10
149 000 000 = 149 • 10 6
Convenzionalmente, per facilitare al massimo i calcoli, quando si scrivono numeri in notazione esponenziale si lascia una sola cifra diversa da zero prima della virgola. I due numeri precedenti diventano allora: 529 • 10 –10 = 5,29 • 10 –8 e 149 • 10 6 = 1,49 • 10 8
Un numero espresso con la notazione esponenziale è costituito da un numero compreso tra 1 e 10, moltiplicato per una potenza di 10. L’esponente della potenza, detto anche ordine di grandezza del numero, è dato dal numero di posti di cui è stata spostata la virgola rispetto al numero originale ed è positivo se la virgola è stata spostata verso sinistra ( il numero originale è maggiore di 1), mentre è negativo se la virgola è stata spostata verso destra ( il numero originale è minore di 1). All’ordine di grandezza corrisponde in genere un prefisso ed un nome, secondo la tabella in alto.
Nelle operazioni coi numeri espressi secondo la notazione esponenziale si opera separatamente sui numeri decimali e sulle potenze di dieci, applicando a queste ultime le proprietà delle potenze elencate nella tabella a lato.
Misure di distanza
Si definisce metro la distanza tra due tacche incise su di una sbarra metallica conservata nell’Ufficio Internazionale dei Pesi e delle misure di Sèvres, presso Parigi.
Nella misura con metodo diretto la grandezza da misurare viene direttamente messa a confronto con una unità di misura appropriata alle sue dimensioni. La scelta dello strumento per effettuare una misura dipende dalla quantità da misurare e dalla precisione richiesta. Ogni strumento di misura è caratterizzato da una portata, che corrisponde alla massima misura eseguibile con lo strumento; e da una sensibilità, uguale alla minima misura leggibile sullo strumento stesso. Così per misurare un quaderno utilizzerò un righello, di portata pari a 50 cm e di sensibilità pari ad 1 mm, per misurare il cortile della scuola utilizzerò una bindella metrica, di portata pari a 50 m e di sensibilità pari ad 1 cm, mentre per misurare lo spessore di una mina da matite utilizzerà un calibro, con portata pari a 10 cm e sensibilità pari a 0,1 mm.
Nelle misure eseguite con metodo indiretto, le grandezze da misurare sono troppo grosse per essere misurate direttamente e la misura si affida allora a calcoli matematici. Ne sono esempi la misura della distanza di due città effettuata su di una carta, oppure con il contachilometri di un’auto.
La misura della superficie, se l’oggetto da misurare ha forma regolare, viene eseguita con metodo indiretto, attraverso il calcolo dell’area della figura corrispondente (vedi tabella 3 pagina 19 Randazzo Stroppa). Se l’oggetto ha invece forma irregolare si ricorre a metodi diretti (vedi figura 13 pagina 19 Randazzo Stroppa). E’ importante ricordare che, poiché 1 m2 = 1 m x 1 m, → 1 m2 = 10 000 cm2.

La misura del volume, se l’oggetto è un solido regolare, viene effettuata con metodo geometrico, mentre se l’oggetto è un liquido essa si ricava da quella del volume del recipiente occupato. Se il solido ha forma irregolare lo si immerge in un liquido ed il suo volume corrisponderà a quello del liquido spostato (vedi figura). E’ importante ricordare che la lettura del livello dell’acqua deve essere effettuata all’altezza del livello inferiore del menisco (vedi figura). Inoltre non dobbiamo dimenticare che talvolta il volume totale di due materiali può essere diverso dalla somma dei loro volumi iniziali (vedi fig. 17 pag. 21 Randazzo Stroppa). Infine, poiché 1 m3 = 1 m x 1 m x 1 m, → 1 m3 = 1 000 dm3. Per le misure del volume dei liquidi si usa spesso anche il litro, ove 1L = 1 000 cm3, per cui 1mL = 1 cm3.
Gli errori della misura
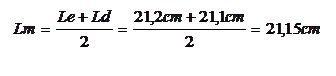Qualsiasi misura di grandezza fisica è sempre affetta da errore, qualunque sia la sensibilità dello strumento o il metodo impiegato. Le misure non sono quindi mai esatte, possono però essere più o meno precise; per aumentare la precisione debbo ridurre l’incertezza, migliorando la procedura oppure utilizzando strumenti migliori. Possiamo innanzitutto valutare l’incertezza di una misura dalla sensibilità dello strumento utilizzato. Così se effettuiamo una singola misura di un quaderno con un righello la cui sensibilità sia 1 mm, possiamo ad esempio trovare che la sua lunghezza è compresa tra 21,1 e 21,2 cm, ovvero 21,1 < L < 21,2; il valore inferiore è approssimato per difetto (Ld), mentre quello maggiore è approssimato per eccesso (Le). Il valore più probabile della misura corrisponde al valore medio (Lm), corrispondente alla semi somma, o media, delle misure per eccesso e per difetto.

Errore assoluto

Il valore medio presenta un’incertezza pari, al massimo, al suo errore assoluto (eass), corrispondente alla semi differenza dei due valori misurati. Nel caso di una misura singola l’errore assoluto è pari a metà della sensibilità dello strumento utilizzato per la misura. Il risultato della misura si indica quindi come: L = Lm ± eass, a significare che il valore reale della grandezza può variare tra (Lm + eass) e (Lm - eass). L’errore assoluto va espresso nella stessa unità di misura della grandezza misurata, per cui nel nostro caso avremo: L = (21,15 ± 0,05) cm . Possiamo quindi concludere che l’errore assoluto indica l’ambito in cui posso trovare valori validi.

Errore relativo ed errore percentuale

L’errore assoluto non è sufficiente per valutare la precisione di una misura, in quanto questa dipende anche dalla quantità che deve essere misurata. Così, ad esempio, se un errore assoluto di 0,5 mm è accettabile per la misura di un quaderno, e trascurabile per quella di una stanza, è inaccettabile per la misura di una lamina metallica. Si ottiene invece una valutazione quantitativa della precisione se si considera l’errore relativo (erel) risultante dal rapporto tra l’errore assoluto e la grandezza da misurare ( o il suo valore medio). Essendo il rapporto tra due quantità espresse con la stessa unità di misura, l’errore relativo è un numero puro, ovvero una grandezza adimensionale. Per comprendere meglio il significato dell’errore relativo proviamo a fare altri esempi. Se consideriamo infatti un errore assoluto di 0,5 mm nella misura di un’aula di 5 metri troviamo un errore relativo pari a 0,0001 (23 volte inferiore a quello del quaderno), mentre nel caso di una lamiera dello spessore di 2,5 mm esso darebbe luogo ad un errore relativo pari a 0,2 (quasi 100 volte superiore a quello del quaderno).
Poiché l’errore relativo è sempre un numero molto piccolo è più comodo considerare l’errore percentuale (e%), che si ottiene moltiplicando per 100 l’errore relativo della stessa misura. Nei tre casi prima considerati avremo dunque:
e% (quaderno) = 0,23%; e% (aula) = 0,01%; e% (lamina) = 20%;
In conclusione l’errore relativo e quello percentuale indicano quanto il mio errore sia significativo in relazione al problema che sto trattando. Infatti la precisione di una misura deve essere valutata in relazione con gli scopi della misura stessa, in base ai quali vanno scelti gli strumenti e le procedure per effettuarla, in quanto più la misura è precisa e più è costoso realizzarla. Per esempio, può essere utile approssimare l’altezza di una quaderno al centimetro, quando essa deve servire solo per distinguere tra loro quaderni di vario tipo; può essere utile approssimarla al millimetro, quando si deve valutare se il quaderno può entrare in un determinato scaffale; può essere necessario approssimarla al decimo di millimetro quando si deve impostare nella cartiera la macchina che effettuerà il taglio dei fogli per la sua produzione.

L’incertezza della misura
Cerchiamo ora di conoscere i principali tipi di errori che si commettono nell’esecuzione di una misura, valutandone le procedure di riconoscimento, di prevenzione e di correzione.

Errori banali

Nel caso di misura diretta sono dovuti a sbagli effettuati durante le operazioni di misura, per distrazione, lettura o trascrizione sbagliata nel caso invece di misura indiretta sono dovuti ad errori nei calcoli. Essi sono riconoscibili in quanto forniscono valori che si discostano molto da gli altri misurati o attesi.
Lunghezza di un’aula: a) 5,34m; b) 5,37m; c) 53,5m; d) 5,36m; e) 5,34m.

Errori sistematici

Si ripresentano regolarmente tutte le volte che si esegue una misura e sono dovuti a limitazioni o difetti dello strumento utilizzato o dell’operazione di misura. E’ ad esempio un errore sistematico quello di misurare la lunghezza di un oggetto senza allineare correttamente il bordo dello stesso con lo zero della scala (vedi figura sotto); parimenti si commette un errore sistematico leggendo uno strumento, come ad esempio una bilancia, che non si azzera perfettamente, oppure utilizzando un orologio che va avanti o indietro. Solitamente gli errori sistematici influenzano la misura sempre nello stesso senso.

Errori casuali

Sono dovuti a cause sconosciute o a fenomeni di cui è impossibile prevedere gli effetti e non si possono quindi eliminare. Ad esempio, la prontezza con cui un operatore preme il tasto di un cronometro al passaggio di un oggetto da un traguardo dipende dai tempi di risposta dell’operatore medesimo, che variano da persona a persona ed in funzione della situazione di attenzione o di stanchezza dell’operatore: difficilmente prove ripetute potranno dare gli stessi risultati. Misurando ripetutamente la lunghezza di un oggetto di legno con un metro si otterranno probabilmente valori diversi perché, ad esempio, non sempre il metro viene posto nella stessa posizione e l’oggetto può avere lunghezza diversa da punto a punto, anche se le differenze non sono apprezzabili ad occhio nudo (far misurare uno stesso alunno da diversi suoi compagni e confrontare i risultati). Per ridurre l’incidenza di tali errori sulla misura si effettuano misure ripetute della stessa grandezza e se ne fa poi la media aritmetica; tale operazione ha il vantaggio di compensare tra loro le misure errate per eccesso con quelle errate per difetto. Tuttavia la media non costituisce il valore reale della misura, ma solo quello che possiamo ritenere sia il più probabile. Riprendendo ad esempio le misure dell’aula prima riportate in precedenza, una volta che sono stati eliminati gli errori banali e/o sistematici, il valore più probabile della lunghezza sarà:

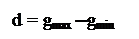Dispersione

La dispersione (d) di una sequenza di valori misurati di una determinata grandezza rappresenta la differenza tra il valore massimo ed il valore minimo misurato. Essa influenza il grado di attendibilità, ovvero l’incertezza, del valore medio, che aumenta quanto più le misure sono sparpagliate intorno ad esso. Nel caso della lunghezza dell’aula prima esaminata la dispersione è

Analogamente a quanto abbiamo già visto per una misura singola, l’errore assoluto (eass) del valore medio si definisce come la semidispersione delle misure effettuate. Il valore della grandezza misurata deve quindi essere espresso come:
Nel caso dell’aula la misura diviene quindi:
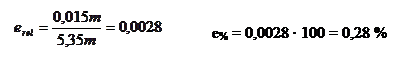Come già visto per le misure singole gli errori sono dati dalle seguenti espressioni:

Numeri approssimati e cifre significative

Poiché ogni misura è affetta da errore, i risultati delle misure vanno espressi da numeri che devono essere usati compatibilmente all’errore stesso: si parla quindi di numeri approssimati fino ad una certa cifra ( a meno di una certa cifra). Per approssimare un numero dobbiamo trascurarne alcune cifre; a tal fine si conviene che l’ultima cifra considerata rimanga invariata se la prima cifra trascurata è minore di 5 (approssimazione per difetto), mentre la si aumenta di una unità se la prima cifra trascurata è maggiore o uguale a 5 (approssimazione per eccesso). Si dice poi che un numero è approssimato a meno dell’ultima cifra considerata.
Se vogliamo ad esempio approssimare il numero 27,3680237 a meno di un milionesimo si ottiene 27,368024 e si dice anche che il numero è approssimato a meno della sesta cifra decimale. Lo stesso numero può inoltre essere variamente approssimato in altri modi ottenendo:
Dobbiamo osservare che gli zeri dopo la virgola, che non hanno significato dal punto di vista matematico, ne acquistano dal punto di vista fisico, in quanto indicano l’approssimazione con cui viene indicato il numero. Ad esempio 27 g e 27,00 g indicano due misure con diversa approssimazione: a meno del grammo, la prima, a meno del centigrammo la seconda. E’ quindi necessario definire quali sono le cifre significative che esprimono la misura, che dipendono dagli strumenti utilizzati per effettuarla. Se ad esempio utilizziamo una bilancia che apprezza il milligrammo sarà corretto esprimere una pesata come 7,023 g, mentre non avrebbe senso la scrittura 7,0230 g; analogamente misuriamo una lunghezza con un metro la cui sensibilità sui un millimetro potremo esprimere una misura come 42,1 cm, mentre non avrebbe senso esprimerla come 42,100, in quanto non abbiamo effettivamente misurato decimi e centesimi di millimetro. Un maggior numero di cifre significative si può ottenere solo utilizzando uno strumento più preciso, cioè con una sensibilità superiore.
In generale si definisce gruppo di cifre significative quello che inizia da sinistra con la prima cifra non nulla e termina a destra con l’ultima cifra nota, anche se questa è zero e/o anche se su di essa grava l’intervallo di incertezza . Per orientarsi si possono ricordare le seguenti regole:

Ogni cifra diversa da zero è cifra significativa; così 152 cm ha tre cifre significative, mentre 2511 Km ne ha quattro;
Ogni zero compreso tra numeri diversi da zero è cifra significativa; ad esempio 207 g ha tre cifre significative, mentre 50,102 Kg ne ha cinque;
Ogni zero a sinistra della prima cifra diversa da zero non è una cifra significativa ovvero per i numeri decimali minori di uno sono significativi solo gli zeri alla fine dello stesso o quelli interposti tra numeri diversi da zero; ad esempio 0,007 mm ha una sola cifra significativa, in quanto può essere espresso attraverso la notazione esponenziale come 7 • 10 –3 mm, 0,20 ha due cifre significative e 0,4002 kg ne ha quattro;
Per ogni numero decimale maggiore di uno sono significative tutte le cifre scritte a destra della virgola; ad esempio 40,20 m ha quattro cifre significativa, in quanto la distanza è stata evidentemente misurata con uno strumento che apprezza i centimetri.

Riguardo alle regole di calcolo, ricordando che il numero di cifre significative dipende dal modo e dallo strumento usato nelle misure, possiamo dare le seguenti:

1) Prodotto o quoziente del risultato di una misura per un numero adimensionale
Il prodotto o quoziente di una misura per un numero adimensionale (che non possiede cifre significative) deve avere lo stesso numero di cifre significative (e quindi la stessa precisione ed approssimazione) della misura di partenza. Ad esempio 0,6584 · 9 = 5,926 (4 cifre significative come la misura di partenza)
2) Addizione o differenza di misure
Il risultato dell’addizione o della differenza di misure deve avere le stesse cifre significative a destra della virgola (e quindi la stessa precisione ed approssimazione) della misura meno precisa. Ad esempio 3562,1 + 0,1948 = 3562,3. In pratica quando i dati da sommare o da sottrarre sono numeri interi oppure hanno lo stesso numero di cifre decimali, si eseguono le operazioni senza alcun vincolo (ad es. 47,75 t + 2,81 t = 50,56 t; 118,9 s - 27,6 s = 91,2 s). Quando invece i dati contengono un numero diverso di cifre decimali si deve arrotondare il risultato in modo che esso abbia cifre decimali pari al dato che ne ha di meno ( ad es. 58,6 cm + 13,72 cm = 72,3 cm; 17,28 s – 4,6 s = 12,7 s) .
3) Moltiplicazione o divisione di due misure
In una moltiplicazione o divisione di due misure il risultato deve avere lo stesso numero di cifre significative (e quindi la stessa precisione ed approssimazione) della misura meno precisa. Ad esempio 3,14 · 8,1248 = 25,5 (3 cifre significative soltanto). Oppure immaginiamo di dover calcolare l’area di un rettangolo la cui base è 28,2 cm e l’altezza 49,4 cm. Il risultato della moltiplicazione è 1393,08 cm2, che però, dovendo avere solo 3 c.s. conviene approssimare a 1,39· 10 3 cm2. Talvolta la calcolatrice tascabile può invece far sparire cifre significative: immaginiamo ad esempio di voler calcolare la base di un rettangolo di area 242 cm2, con altezza di 12,1cm. Il risultato della divisione è 20 cm, che però più esattamente va scritto come 20,0 ( tre c.s.).

4) Elevamento a potenza ed estrazione di radice
Tali operazioni non pongono problemi nuovi, in quanto sono riconducibili a moltiplicazioni, per cui valgono le medesime regole già viste per queste ultime. Quindi sia nell’elevamento a potenza, che nell’estrazione di radice, il risultato deve avere lo stesso numero di c.s. del dato di partenza.
5) Equivalenze
Nel trasformare un dato tramite un’equivalenza, il numero di cifre significative deve restare uguale a quello del dato di partenza.
6) Svolgimento di più calcoli in successione
In questo caso si possono applicare le regole già viste ad ogni singolo passaggio. E’ tuttavia possibile svolgere anche tutti i calcoli assieme (magari con la calcolatrice) ed assegnare poi al risultato finale il numero di c.s. del dato che ne ha meno.

Propagazione dell’errore

Moltiplicando o dividendo una misura per un numero adimensionale anche il suo errore assoluto deve essere moltiplicato o diviso per lo stesso numero.
L’errore assoluto per una somma o per una differenza di misure è dato dalla somma degli errori assoluti delle singole misure.
L’errore relativo sul prodotto di due misure è pari alla somma degli errori relativi sulle singole misure.

MISURE DI MASSA

Passando da una unità più grande ad una più piccola moltiplico per 10, spostando la virgola verso destra di un posto

kg
chilogrammi

hg
ettogrammi

dag
decagrammi

g
grammi

dg
decigrammi

cg
centigrammi

mg
milligrammi

Passando da una unità più piccola ad una più grande divido per 10, spostando la virgola verso sinistra di un posto

milli

Un millesimo

1/1000

centi

Un centesimo

1/100

1kL = 1m3

deci

Un decimo

1/10

1L = 1dm3

unità

1mL = 1cm3

deca

etto

100

chilo

1000

MISURE DI CAPACITA’

Passando da una unità più grande ad una più piccola moltiplico per 10, spostando la virgola verso destra di un posto

kL
chilolitri

hL
ettolitri

daL
decalitri

L
litri

dL
decilitri

cL
centilitri

mL
millilitri

Passando da una unità più piccola ad una più grande divido per 10, spostando la virgola verso sinistra di un posto

MISURE DI LUNGHEZZA

Passando da una unità più grande ad una più piccola moltiplico per 10, spostando la virgola verso destra di un posto

km
chilometri

hm
ettometri

dam
decametri

m
metri

dm
decimetri

cm
centimetri

mm
millimetri

Passando da una unità più piccola ad una più grande divido per 10, spostando la virgola verso sinistra di un posto

MISURE DI SUPERFICIE

Passando da una unità più grande ad una più piccola moltiplico per 100, spostando la virgola verso destra di due posti

km2

hm2

dam2

dm2

cm2

mm2

Passando da una unità più piccola ad una più grande divido per 100, spostando la virgola verso sinistra di due posti

MISURE DI VOLUME

Passando da una unità più grande ad una più piccola moltiplico per 1000, spostando la virgola verso destra di tre posti

km3

hm3

dam3

dm3

cm3

mm3

Passando da una unità più piccola ad una più grande divido per mille, spostando la virgola verso sinistra di tre posti

Svolgere le seguenti equivalenze, utilizzando ove necessario anche la notazione esponenziale

Lunghezza

0,88 dm2 =

mm2

6,2 dm3 =

1,39 dam =

11,9 m2

dm2

13,9 m3 =

11,71 Km =

9.11 hm2 =

dam2

22,8 mL =

cm3

215 cm =

23000 dam2 =

km2

2,5 L =

cm3

0,11 m =

910 hm2 =

km2

9,1 km3 =

415 dam =

1,25 hm2 =

3,4 dm3 =

82,6 dm =

0,98 m2 =

cm2

17500 cm3 =

7849 mm =

23.600 m2 =

hm2

2680 L =

23,87 hm =

4,8 cm2

mm2

280 mL =

dm3

0,23 km =

dam

9600 dm2 =

dam2

25,1 m3

615,22 m =

3,5 km2 =

4,7 km3

929 dm =

dam

1,2 m2 =

mm2

Massa

0,21 hm =

Volume e capacità

1.456 g =

0,025 km =

5,3 m3 =

dm3

12.300 g =

259,11 mm =

0.035 km3 =

hm3

12,3 hg =

0,236 dam =

4500 mm3 =

dm3

0.99 kg =

0,003 Km =

0.125 L =

0.69 dag =

Superficie

49,21 hL =

0.56 hg =

45,1 dam2 =

28900 dm3 =

3,5 kg =

6,23 Km2 =

hm2

167 cL =

4,8 hg =

11.590 cm2 =

dm2

8,9 m3 =

mm3

6 · 105 mg

ESERCIZI SULLE MISURE

Notazione esponenziale
Ricordiamo che nelle equivalenze il valore dei numeri deve restare lo stesso, quindi:

Se sposto la virgola a sinistra di un posto divido il numero per 10 e quindi devo anche alzare l’esponente di una unità

1,00 •106 = 0,1•107 = 0,01•108 = 0,001•109 = 0,0001•1010

Se sposto la virgola a destra di un posto moltiplico per 10 e quindi devo anche abbassare l’esponente di una unità

1,00 •106 = 10,0 •105 = 100 •104 = 1 000 •103 = 10 000 •102 = 100 000 •101 =
= 1000 000 •100
Scrivi in numeri decimali i seguenti numeri espressi in notazione esponenziale
1) 1,00 •105 =                                     2) 1,00 •108 =
3) 3,25 •1012 =                                              4) 1,2 •10-3 =
5) 2,5 •10-10 =                                     6) 1,5 •106 =
7) 2 •10-7 =                                          8) 2,12 •102 =
9) 1,3 •10-4 =                                      10) 1.00•10 6 =
11) 3.52•10 9=                                   12) 2.5•10 –5=
13) 3.24•10 –3 =

Scrivi in notazione esponenziale i seguenti numeri decimali
14) 0,35 =                                                   15) 18 000 =
16) 2 400 =                                        17) 0,000000042 =
18) 0,00087 =                                    19) 75 milionesimi =
20) 0.000236 =                                  21) 93.2 miliardi =
22)1 550 000 =                                           23) 3 897 000 =
24) 0,0000345 =                                25) 0,0000012 =
26) 1/100 000 =                                 27) 150 000 =
28) 0.000323 =                                           29) 2 000 000 000 =
30) 0.000000012 =                            31) 0.00000526 =
32) 145 000 000 =                             33) 243 000•10-3 =
34) 0.00000062•109=

Eseguire le seguenti operazioni:
a) 1,4 •102 X 5 •104 =
Equivalenze
Lunghezze
a) 417 mm = dam                   b) 4,2 km = m                          c) 12 mm = m
d) 0,05 hm = cm                              e) 125 cm = m                                   f) 1712 cm = hm
g) 82,6 dm = mm                    h) 615 m = km

i) se un batterio ha un diametro di 5 μm, quanti batteri potranno entrare in un metro? quanti in un millimetro?
l) se un virus ha il diametro di 50 nm, quanti virus potranno entrare in un metro?, quanti in un millimetro?

Superficie
a) 12 km2 = dam2 b) 2 m2 = mm2 c) 15 500 cm2 = m2
d) 0.325 m2= dm2 e) 97000 cm2 = m2 f) 11 km2 = m2

Volume e capacità
a) 1,4 m3 = cm3 b) 5.87 m3 = dm3 c) 350 cm3 = m3
d) 2,7 m3 = mm3 e) 412 m3 = mm3 f) 52 m3 = mL
g) 125 L = cm3

Massa
a) 100 mg = kg                      b) 13 g = kg                           c) 2.5 hg = kg
d) 3.2 t = kg                                     e) 0,2 kg = mg
Cifre significative
Eseguire le operazioni esprimendo il risultato con il giusto numero di cifre significative
a) 3562,1 + 0,1948 =                                      b) 88,57 – 5,231 =
c) 3,14 · 8,1248 =                                            d) 0,036 : 563 =
e) 12,4 + 8,12 + 0,618 =                                 f) 8,4 – 2,135 =
g) 0,015 · 1,04 =

Proporzioni

Un deposito per la raccolta dell’acqua ha le seguenti dimensioni: 50 cm x 30 cm x 70 cm. Se il tubo che lo riempie porta 5 L di acqua al minuto, quanto tempo sarà necessario al suo riempimento?
Un parallelepipedo di alluminio ha le seguenti dimensioni: 2 cm x 4 cm x 1 cm. Se un decimetro cubo di alluminio pesa 2,7 kg, quanti grammi peserà il parallelepipedo?
In un litro di birra a 6° alcolici ci sono 60 mL di alcol. Se un litro di alcol pesa 0,8 kg, quanti grammi di alcol si introducono nell’organismo bevendo una lattina da 33 cL di quella birra?
Un insegnante guadagna 1300 euro al mese; il 15% dello stipendio è destinato a pagare un debito con una banca del valore di 50 milioni di lire. Se un euro vale 1936,27 lire, quanti mesi saranno necessari per pagare l'intero debito?
Consideriamo che nell’oro a 18 carati sia presente il 75% di oro puro ed il 25 % di rame. Quanto peserà un oggetto di oro del volume di 6 mL, se un dm3 di rame pesa 8,9 kg, mentre un dm3 di oro pesa 19,3 kg?
Un muratore deve costruire un muro in mattoni con le seguenti misure: 2,5 m x 4,8 m x 18 cm. Se ogni mattone ha un volume di 700 cm3, quanti mattoni dovrà utilizzare? Se il materiale con cui sono fatti i mattoni pesa 2,7 kg ogni dm3, quanti quintali peserà il muro?

SOLUZIONI

Notazione esponenziale
Scrivi in numeri decimali i seguenti numeri espressi in notazione esponenziale
1) 100 000;             2) 100 000 000;            3) 3 250 000 000 000;            4) 0,0012;
5) 0,00000000025;          6) 1 500 000;            7) 0,0000002;
8) 212;                        9) 0,00013.                   10) 1 000 000;
11) 3 520 000 000;         12) 0.000025;            13) 0.00324;
Scrivi in notazione esponenziale i seguenti numeri decimali
14) 3,5 •10-1;           15) 1,8 •104;                16) 2,4 •103;            17) 4,2 •10-8;
18) 8,7 •10-4            19) 0.000075 = 7.5 •10 –5;                       20) 2.36 •10 –4;
21) 93 200 000 000 = 9.32 •1010           22) 1.55 •10 6;            23) 3,897 •106;
24) 3,45•10-5;             25) 1,2 •10-6;             26) 1•10-5;           27) 1.5•105;
28) 3.23 •10 -4;            29) 2•10 9;                30) 1.2•10 -8;       31) 5.26•10-6;
32) 1.45•108;              33) 2.43•102;           34) 6.2•102;

Eseguire le seguenti operazioni: a) 7 •106;
Equivalenze
Lunghezze
a) 0,0417 dam; b) 42 000 m; c) 0,012 m; d) 500 cm;
e) 1,25 m; f) 0,1712 hm; g) 8260 mm; h) 0,615 km.
i) (200.000 in un metro), (200 in un millimetro)
l) (20.000.000 in un metro), (20.000 in un millimetro)

Superficie
a) 120 000 dam2; b) 2•106 mm2; c) 1,55;
d) 32.5 dm2; e) 9.7 m2; f) 1,1 107 m2

Volume e capacità
a) 1,4 •106 cm3; b) 5870 dm3; c) 0.00035 m3
d) 2,7 •109 mm3; e) 4,12 •1011 mm3; f) 5,2 •107 mL; g) 1,25 •103 cm3;

Massa
a) 0.0001 kg; b) 0.013 kg; c) 0.25 kg; d) 3200 kg e) 2•105 mg;
Cifre significative
c) 25,5, d) 0,000064; e) 21,1; f) 6,3; g) 0,016;

Proporzioni
1) 21 minuti; 2) 21,6 g; 3) 15,84 g; 4) 132 mesi;
5) 100,2 g (Cu 13,35 g + Au 86,85 g); 6) 3085 mattoni; 58,32 q

Randazzo, Stroppa – Scienza della materia – Arnoldo Monadori Scuola; pag.12

In questo caso l’errore deriva dalla sensibilità dello strumento, indipendentemente dalla procedura seguita.

Olmi, Pera – Chimicamente –Mc Grow Hill 1998 pp. 17 – 18
Silvi, Bertoletti – Laboratorio di fisica – D’Anna 1984 pp. 21 - 23

Perché è stata approssimata.

Bagatti, Corradi, Desco Ropa – Chimica (seconda edizione) – Zanichelli, appendice

Silvi, Bertoletti – Laboratorio di fisica – D’Anna 1984 pp. 32 - 33

Fonte: http://www.liceodavincifi.it/_Rainbow/Documents/LA%20MISURA%20DELLE%20GRANDEZZE.doc

Misura delle grandezze