Il principio di induzione e i numeri naturali
Il principio di induzione e i numeri naturali
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Il principio di induzione e i numeri naturali
Il principio di induzione e i numeri naturali.
Quando nel suo Arithmetices principia Peano introduce i numeri naturali:
1. 1 è un numero,
2. Il successivo di un numero è un numero,
3. 1 non è successivo di nessun numero,
4. Se i successivi di due numeri sono uguali, anche i due numeri sono uguali,
5. Se un insieme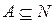 
contiene il numero 1 e il successivo di ogni suo elemento, allora A = N,
il principio di induzione non è che uno degli assiomi che determinano N. Appena però si prosegue la lettura, si vede immediatamente che, benché tutti gli assiomi siano essenziali per caratterizzare il sistema dei numeri naturali, il quinto gioca un ruolo centrale nella definizione delle operazioni con i numeri e nella dimostrazione delle proprietà relative.
Gli assiomi riguardano una sola operazione: il passaggio da un numero intero a al successivo, che indicheremo con S(a). Occorrerà dunque definire a partire da essa le operazioni con i numeri (in particolare la somma e il prodotto) e dimostrarne le principali proprietà.
Cominciamo con la somma. Per sommare ad a il numero 1, basterà prendere il successivo di a: a + 1 = S(a). La somma di due numeri interi a + b è più complicata. Intuitivamente, si può pensare di sommare successivamente ad a tante unità quante sono contenute in b; ossia, partendo da a, di ripetere b volte
l’operazione di passaggio al successivo:
a + b = S(S(. . . S(a)) . . .) b volte.
I puntini fanno pensare che la definizione non sia così esplicita come sarebbe necessario: qualcosa è lasciata sottintesa. In genere, ogni volta che in una formula compaiono dei puntini, c’è un uso implicito del principio di induzione. E infatti la definizione più corretta della somma fa appunto uso di questo assioma:
Definizione 1 (Somma) La somma a+b di due numeri naturali a e b è definita dalle relazioni seguenti:
a + 1 = S(a)
a + (b + 1) = (a + b) + 1 = S(a+b). (A)
A questa definizione Peano aggiunge una nota esplicativa:
Questa definizione si deve leggere così: se a e b sono numeri, e se a+b è un numero [cioè se è stato definito], ma a+(b+1) non è stato ancora definito, allora a + (b + 1) significa il numero che segue a + b.
Abbiamo qui un esempio di definizione ricorsiva. Intuitivamente, la prima relazione definisce la somma a + b per b = 1; la seconda ci dice che se essa è definita per b, lo è anche per b + 1. Di conseguenza, la somma è definita per ogni numero b.
Veniamo ora brevemente alle principali proprietà della somma.
Teorema 1 (Proprietà associativa) Per ogni terna di numeri a, b e c si ha
(a + b) + c = a + (b + c). (B)
Dimostrazione. La (B) è vera per c = 1; infatti in questo caso non è altro che la (A). Supponiamo ora che sia vera per c e dimostriamola per c + 1. Si ha
(a + b) + (c + 1) =(A) [(a + b) + c] + 1 =(B) [a + (b + c)] + 1 =(A) a + [(b + c) + 1] =(A) a + [b + (c + 1)].
Per il principio di induzione, la (B) vale allora per ogni c, e il teorema è dimostrato.
Per la proprietà commutativa bisognerà procedere in due tappe.
Lemma 1. Per ogni intero a si ha a + 1 = 1 + a. (C)
Dimostrazione. La (C) è vera per a = 1. Se supponiamo che sia vera per a, si ha
(a + 1) + 1 =(C) (1 + a) + 1 =(A) 1 + (a + 1)
e il lemma è dimostrato.
Teorema 2 (Proprietà commutativa della somma.) Per ogni coppia di numeri naturali a e b risulta
a + b = b + a. (D)
Dimostrazione. Per il lemma precedente la (D) è vera per b = 1. Supponiamo ora che sia vera per b, e dimostriamola per b + 1. Si ha
a + (b + 1) =(A) (a + b) + 1 =(D) (b + a) + 1 =(A) b + (a + 1) =(C) b + (1 + a) =(B) (b + 1) + a
e la (D) è dimostrata per b+1. Per il principio di induzione, la (D) varrà allora per ogni b.
Veniamo ora al prodotto. Anche per questa operazione occorrerà dare una definizione ricorsiva:
Definizione 2 (Prodotto) Il prodotto ab di due numeri naturali è definito dalle relazioni:
a · 1 = a
a(b + 1) = ab + a. (E)
Teorema 3 (Proprietà distributiva) Risulta
(a + c)b = ab + cb. (F)
Dimostrazione. Per b = 1 la (F) segue dalla definizione precedente. Supponiamo che valga per b e dimostriamola per b + 1. Si ha
(a + c)(b + 1) =(E) (a + c)b + a + c =(F) ab + cb + a + c =(D) ab + a + cb + c =(E) a(b + 1) + c(b + 1).
La (F) vale dunque per b + 1, e il teorema è dimostrato.
Lemma 2. Si ha 1 · a = a.
Dimostrazione. La relazione è valida per a = 1. Supponiamo che valga per a; si ha allora
1 · (a + 1) = 1 · a + 1 = a + 1
e dunque vale anche per a + 1.
Dal lemma precedente e dalla (F) segue che
ba + a = ba + 1 · a =(F) (b + 1)a.
Teorema 4 (Proprietà commutativa del prodotto) Per ogni a e b in N risulta
ab = ba. (G)
Dimostrazione. Per il lemma precedente e la definizione di prodotto, la (G) vale per b = 1. Supponiamo ora che valga per b; si ha
a(b + 1) =(E) ab + a =(G) ba + a = (b + 1)a
e quindi vale per b + 1. Per il principio di induzione, essa vale per ogni b.
In maniera analoga si può definire la potenza ab mediante le relazioni a1 = a, ab+1 = aba. Lasciamo al lettore la dimostrazione delle proprietà
ab+c = ab ac
(ab)c = ac bc
(ab)c = abc.
Fonte: http://univaq.it/~leonetti/ssis/schede/09_Il_principio_di_induzione_e_i_numeri_naturali.doc
Sito web da visitare: http://univaq.it
Autore del testo: non indicato nel documento di origine
Nota : se siete l'autore del testo sopra indicato inviateci un e-mail con i vostri dati , dopo le opportune verifiche inseriremo i vostri dati o in base alla vostra eventuale richiesta rimuoveremo il testo.
Parola chiave google : Il principio di induzione e i numeri naturali tipo file : doc
Il principio di induzione e i numeri naturali
Visita la nostra pagina principale
Il principio di induzione e i numeri naturali
Termini d' uso e privacy