Appunti di statistica

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Appunti di Statistica

Definizione
La statistica è una scienza che si propone di definire con dei numeri cose che non si possono numerare ne misurare.

Processo statistico
L’indagine statistica comprende le seguenti fasi:
Campionamento. Consiste nel selezionare la popolazione di componenti da studiare. La popolazione può essere popolazione campione (e generalmente viene scelta con modalità random) o popolazione obiettivo (generalmente selezionata secondo criteri ben precisi; es. la popolazione di pazienti con epatite).
Raccolta dati. Generalmente si utilizzano i fogli elettronici (es. Excel), perché consentono una facile manipolazione ed elaborazione dei dati.
Rappresentazione. Può essere grafica o numerica.
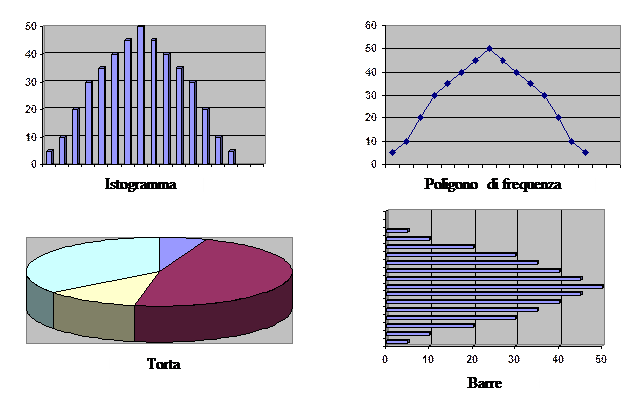Grafica. Si possono utilizzare diverse forme di rappresentazione grafica. Le più utilizzate sono: l’istogramma, il poligono di frequenza, la torta e le barre.

Numerica. I parametri più rappresentativi sono:

Media (somma dei singoli casi diviso il numero di casi sommati)
Range (valore più alto e più basso … dei dati raccolti)
Mediana (il valore che taglia a metà i valori raccolti; es. 2, 4, 5, 7, 8, 11, 14. Mediana=7).
Moda (il valore che si verifica con maggiore frequenza).
Deviazione standard (DS) (indica la dispersione dei valori attorno alla media). Specificatamente, m±DS à raggruppa il 68% dei valori.

m±2DS à raggruppa il 95% dei valori.
m±3DS à raggruppa il 99% dei valori.

Distribuzione di una popolazione. Quando i valori raccolti vengono rappresentati graficamente (es. istogramma o poligono di frequenza) possono presentare due diverse forme di distribuzione:
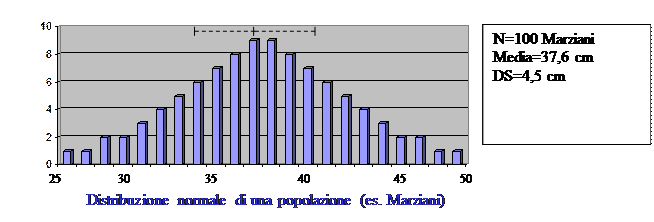- distribuzione normale (o gaussiana o a campana), in cui media, mediana e moda coincidono. In questo caso la media e la deviazione standard descrivono correttamente la popolazione.

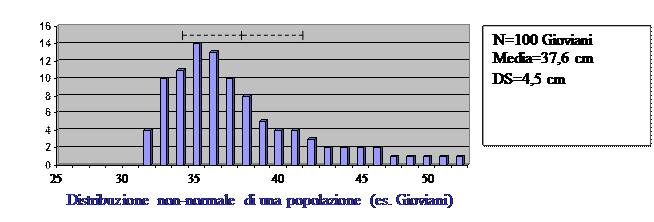- distribuzione non-normale in cui media, mediana e moda non coincidono. In questo caso la media e la deviazione standard non descrivono correttamente la popolazione.

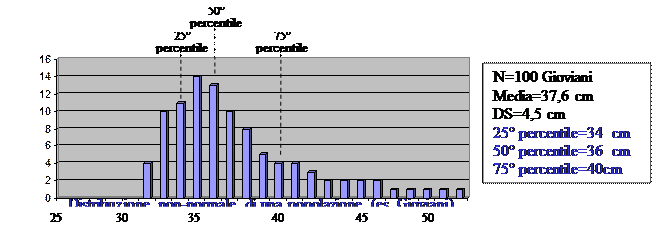
In questi casi (distribuzione non-normale), la distribuzione della popolazione si esprime coi percentili. Coi percentili, la mediana corrisponde al 50° percentile (punto medio). Poi, si possono usare il 25° percentile (mediana – 25%) ed il 75° percentile (mediana+25%) come pure, il 5° percentile (mediana – 45%) ed il 95° percentile (mediana+45%).

Elaborazione dei dati. Esistono numerosi test per l’elaborazione dei dati. Essi comprendono i Test parametrici ed i Test non parametrici.
I Test parametrici sono test che si possono applicare in presenza di una distribuzione normale dei dati. Appartengono ai Test parametrici i seguenti test:

test di Student per dati appaiati,
test di Student per dati indipendenti,
test di correlazione di Pearson.

I Test non parametrici sono test che non necessitano che le grandezze confrontate seguano una certa distribuzione (es. gaussiana). I metodi non parametrici sono particolarmente adatti a confrontare campioni di cui non si conosce o non si può ipotizzarne l'andamento della distribuzione e/o campioni molto piccoli . Appartengono ai Test non parametrici i seguenti test:

test del chi-quadro
test di Fisher,
test U di Mann-Whitney, per confrontare dati tra gruppi indipendenti (analogo del test di Student per dati indipendenti),
test di Wilcoxon, per confrontare dati tra gruppi appaiati, (analogo del test di Student per dati appaiati),
test di correlazione dei ranghi di Spearman (analogo non parametrico del coefficiente di Pearson).

Limiti di confidenza
La media calcolata di una popolazione campione (es. l’altezza di 900 italiani) non necessariamente è rappresentativa della media della popolazione generale di appartenenza (es. la popolazione italiana). I fattori influenzanti la differenza tra le due medie (popolazione campione e popolazione generale) sono essenzialmente due: a) il numero dei componenti della popolazione campione (> sono i componenti e < è la probabilità che la media calcolata sia diversa da quella della popolazione generale); b) la variabilità intrinseca del parametro (altezza) studiato (per es. l’altezza potrebbe variare con le condizioni economiche, coll’esposizione al sole, etc). La discordanza tra media della popolazione campione e media della popolazione generale viene definita Errore Standard (ES):

Errore Standard (ES) =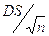
ove, DS e n sono, rispettivamente, la deviazione standard ed il numero dei componenti della popolazione campione (es. se la m±DS della popolazione campione di 900 italiani è 170±15 cm, l’errore standard è 15/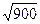 à 15/30 = 0.5).
L’errore standard, in pratica, ci da una stima probabilistica della differenza tra la media del campione testato e quella della popolazione generale di appartenenza.
Si definiscono, invece, limiti di confidenza i valori entro i quali si può presumere che cada, con probabilità prefissata, la media vera della popolazione generale di appartenenza. I limiti di confidenza possono essere

al 68% (m ± 1 ES)
al 95% (m ± 2 ES)
al 99% (m ± 3 ES)

Quelli più utilizzati sono i limiti di confidenza al 95% e l’intervallo compreso tra i due limiti di confidenza (quello inferiore – m-2ES – e quello superiore – m+2ES) si chiama intervallo di confidenza. Nel caso riportato sopra, il calcolo dei limiti di confidenza al 95% sarà dato da
Limite di confidenza inferiore à m-2ES à 170-2*0.5 = 170-1 = 169 cm
Limite di confidenza superioreà m+2ESà 170+2*0.5= 170+1= 171 cm
Pertanto, possiamo asserire che, con una probabilità del 95%, la media della popolazione generale degli italiani è compresa tra 169 e 171 cm.
Attenzione, l’intervallo di confidenza 169-171 cm non ci dice che il 95% delle altezze degli italiani è compresa tra 169 e 171 cm … ma che la media (quella vera) degli italiani è compresa (con una probabilità del 95%) in quello intervallo di valori!

Test di significatività’
E’ un metodo statistico che consente di stabilire se due risultati sono (o meno) significativamente diversi. Per calcolare il test di significatività si parte da un’ipotesi, detta ipotesi nulla, secondo la quale non c’è differenza significativa tra i due risultati. Si stabilisce, quindi, se l’ipotesi nulla è vera o falsa, definendo anche la probabilità che questo sia esatto.
Per convenzione, una probabilità (P) maggiore del 5% (P>0.05) non scarta l’ipotesi nulla, mentre una probabilità inferiore al 5% (P<0.05) scarta l’ipotesi nulla. Inoltre, tanto più il valore di P è inferiore al 5% (es. P>0.01, P<0.005, P<0.001) tanto più la differenza rilevata tra i due risultati è significativa (reale).

P>0.05 à non scarta l’ipotesi nulla (…non c’è una differenza significativa)
P<0.05 à scarta l’ipotesi nulla (… c’è una differenza significativa)

Per es. la media± DS dell’altezza dei pugliesi (calcolata su un campione di 200 persone) risulta essere 170±12 cm, mentre quella dei siciliani (calcolata su un campione di 230 persone) risulta essere 178±11 cm. La domanda che ci si pone è – sono i siciliani più alti dei pugliesi ? – Per poterlo stabilire, si procede nel seguente modo:
- si pone l’ipotesi nulla (secondo la quale la differenza tra i due risultati non è significativa): i siciliani non sono significativamente più alti dei pugliesi.
- poi, si procede all’elaborazione dei dati (mediante test specifici) e si calcola la “P”. Se risulta

P>0.05 à l’ipotesi nulla non è scartata, quindi à i siciliani non sono significativamente più alti dei pugliesi (e questo è vero con una probabilità del 95%).
P<0.05 à l’ipotesi nulla è scartata, quindi à non è vero che i siciliani non sono più alti dei pugliesi à il che equivale a dire che i siciliani sono più alti dei pugliesi (e questo è vero con una probabilità del 95%).
P<0.001 à scarta l’ipotesi nulla, quindi à … i siciliani sono più alti dei pugliesi e questo è vero con una probabilità del 99% (0.001=99/100).

In pratica, il valore di p rappresenta la probabilità di sbagliare affermando che esiste una differenza reale tra 2 risultati.

Due possibili errori che si possono commettere col test di significatività sono i seguenti:
Errore di tipo I (o errore alfa): la differenza tra i due risultati cade proprio nella piccola percentuale (<5%) non compresa dal test di significatività.
Errore di tipo II (o errore beta): la differenza apparentemente significativa è in realtà dovuta al basso numero dei componenti della popolazione campione. Questo accade, in particolare, quando il parametro considerato ha una notevole variabilità. Infatti, quando il parametro da analizzare è molto variabile… c’è bisogno di una popolazione campione costituita da numerosi componenti per non incorrere in un errore di tipo II.

Test parametrici

Test di Student
Il test di Student (t-test) è un tipo di analisi che serve per verificare se ci sono differenze tra due medie. Esso comprende due varianti:
il Test di Student per dati indipendenti, che permette di confrontare due gruppi diversi rispetto ad una singola variabile (es. valutare se l’altezza presenta differenze tra Maschi e Femmine…in questo caso le misurazioni vengono effettuate su soggetti diversi);
il Test di Student per dati appaiati, che permette di confrontare tra loro due misurazioni diverse (variabili) fatte sugli stessi soggetti (es. valutare se la temperatura corporea varia tra mattino e sera … in questo caso le misurazioni vengono effettuate 2 volte, mattina e sera, sugli stessi soggetti).

1° Esempio
Misuriamo l’altezza di 60 alunni maschi di III media italiani e 60 coetanei della Thailandia. I dati ottenuti sono riportati sotto:

Persone del nord Italia	Altezza (cm)	Persone del sud Italia	Altezza (cm)
Gianni	162	Siphong	156
Roberto	159	Onphitak	151
Carlo	165	Tokelau	155
Stefano	157	Siphong	149
Alessandro	161	Tsekim	156
Marco	163	Zombarn	153
…	…	…	…
Media	161		153

L’ipotesi che scaturisce dalla lettura dei dati è la seguente: gli alunni italiani sono più alti dei coetanei Thailandesi in quanto l’altezza media degli alunni italiani è 161 cm contro i 153 cm dei thailandesi.
L’ipotesi nulla, però, sostiene che non c’è differenza significativa tra le due medie. Applichiamo, pertanto il test di Student per dati indipendenti. Immettendo i dati nel computer si ricava un valore di P = 0,001 (valore di significatività). Poichè il valore calcolato di P è 0.001 e poiché esso è minore di 0.05 (P<0.05 … anzi P<0.01) à l’ipotesi nulla è bocciata. Pertanto, si deve concludere che l’ipotesi secondo la quale gli alunni maschi di III media italiani sono più alti dei coetanei thailandesi è vera.

2° Esempio
Un omeopata sostiene che un particolare prodotto omeopatico (Abbassafebbr) è in grado di far abbassare la febbre. Per dimostrare ciò, somministra il prodotto a 50 persone, in occasione di un episodio febbrile, misurando la temperatura prima della somministrazione e 2 ore dopo. I dati ottenuti sono riportati sotto:

PAZIENTE	Temperatura prima della somministrazione	Temperatura dopo 3 ore	Differenza di T prima e dopo il farmaco
Lucia	38,3	38,5	+0.2
Leonardo	39,1	37,6	-1.5
Primiano	40,2	38,3	-1.9
Grazia	37,6	37,5	-0.1
Alfonsina	38,9	36,9	-2.0
Michele	38,7	38,8	+0.1
…	…	…	…
Media	38.8	37.9

L’ipotesi che scaturisce dalla lettura dei dati è la seguente: l’assunzione dell’Abbassafebbr fa abbassare la febbre in quanto la temperatura media 2 ore dopo il prodotto è di 37.9 gradi contro i 38.8 gradi prima dell’assunzione (…con grande esultanza dell’omeopata).
L’ipotesi nulla, però, sostiene che non c’è differenza significativa tra le due medie. Applichiamo, pertanto il test di Student per dati appaiati. Immettendo i dati nel computer si ricava un valore di P = 0,097 (valore di significatività).
Poiché il valore calcolato di P è 0.097 e poiché esso è maggiore di 0.05 (P>0.05) à l’ipotesi nulla non può essere bocciata. Pertanto, si deve concludere che l’ipotesi secondo la quale l’Abbassafebbr fa abbassare la febbre va respinta (ci dispiace … ma non più di tanto, per l’omeopata).

Test di Correlazione di Pearson
E’ una tecnica statistica che serve a stabilire se tra due variabili esiste una relazione. Più specificatamente, la Correlazione valuta la tendenza che hanno due variabili a variare congiuntamente (o a co-variare) (es. “attitudine in matematica” e “profitto in matematica”). Essa viene qualificata sulla base di 3 elementi: a) tipo (o forma) della relazione, b) direzione della relazione e 3) entità della relazione.
Una relazione si dice lineare quando la sua rappresentazione grafica, sugli assi cartesiani, si avvicina alla forma di una retta, non lineare quando ha un andamento curvilineo.
Una relazione si dice positiva quando la sua rappresentazione grafica, sugli assi cartesiani, vista da sinistra a destra tende a “salire”, negativa quando da sinistra a destra tende a “scendere”.
L’intensità della relazione (ma anche la direzione) viene espressa dal coefficiente di correlazione, indicato con la lettera r. r può variare tra –1 e +1. Specificatamente,

Indice di correlazione (r) = 0 à le due variabili non hanno nessuna tendenza a variare assieme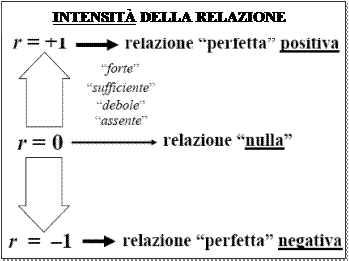
Indice di correlazione (r) = +1 à le due variabili variano congiuntamente e nello stesso senso (relazione positiva; cioè, se aumenta una aumenta anche l’altra) ed in maniera così perfetta che, dato il valore dell’una, si può prevedere con esattezza il valore dell’altra.
Indice di correlazione (r) = -1 à le due variabili variano congiuntamente ma in senso opposto (relazione negativa; cioè, se aumenta una, l’altra diminuisce e viceversa) ed in maniera così perfetta che, dato il valore dell’una, si può prevedere con esattezza il valore dell’altra.
Indice di correlazione (r) = compreso tra 0 e ±1 à le due variabili variano congiuntamente (nello stesso senso – se r è +vo - od in senso opposto – se r è -vo -) ma in maniera non perfetta.

Per il calcolo del coefficiente di correlazione si impiegano diversi metodi, a seconda del tipo di variabile. Per le variabili quantitative si utilizza il coefficiente di Pearson. Il test di correlazione di Pearson da, come risultato, un valore di r, variabile tra -1 e +1, ed un valore di p. Quest’ultimo esprime (come in ogni altro test statistico) il valore di significatività della relazione trovata.
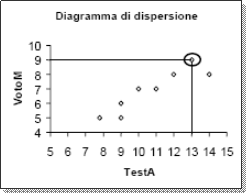
Esempio. Supponiamo di aver eseguito un test di attitudine alla matematica (testA, con punteggio da 0 a 15) e aver svolto un compito di matematica in classe (votoM, con punteggio da 0 a 10) su 8 studenti. I dati ottenuti sono riportati sotto.

Studente	Codice dato	TestA	VotoM
Primiano	1	12	8
Lucia	2	10	7
Amalio	3	14	8
Oriana	4	9	5
Silvio	5	9	6
Ivana	6	13	9
Felicia	7	11	7
Gaetano	8	8	5

Rappresentiamo adesso questi dati. Ad occhio si vede che esiste una relazione lineare e positiva tra le due variabili (testA e votoM) e viene spontaneo avanzare l’ipotesi che l’attitudine alla matematica (variabile “testA”) si correla con il profitto, cioè col punteggio al compito in classe (variabile “votoM”). Per verificare tutto questo, ricorriamo al test di Pearson. Il risultato del test ci da: r= 0.91 e P<0.05. Quindi, possiamo concludere che esiste una relazione lineare, positiva e forte tra l’attitudine alla matematica e il voto riportato al compito in classe. Infatti, maggiore è l’attitudine e maggiore è il voto riportato al compito (r = .91). La probabilità che tutto questo è errato è inferiore al 5% (perché p<0.05).
Alcune precisazioni sul test di correlazione.
1) Il coefficiente di correlazione r misura solo la tendenza che 2 variabili hanno a variare congiuntamente. Questo, però, non implica che tra le due variabili ci sia un nesso causale! Per es. la correlazione dimostrata tra attitudine alla matematica e voto al compito in classe non implica necessariamente che “chi ha una buona attitudine alla matematica avrà ottimi voti al compito in classe” (rapporto causale). Infatti, potrebbe benissimo accadere che ragazzi con bassa attitudine ottengano alti voti al compito in classe e, viceversa, ragazzi con elevata attitudine, voti bassi (perché, per esempio, i ragazzi con bassa attitudine si sono applicati allo studio della matematica più dei loro amici maggiormente dotati).
2) Quando il coefficiente di correlazione r è 0 implica solo che non c’è correlazione lineare tra le due variabili … esso non esclude che ci possa essere una correlazione non lineare !

Test non parametrici

Test del Chi-2 (Chi-quadro)
Il Chi-2 (c2) è un tipo di analisi che serve per verificare se ci sono differenze tra due percentuali di una stessa popolazione .

Calcolo di una percentuale
La percentuale (%) si calcola dividendo il numero di casi dei quali si intende valutare la percentuale per il numero totale dei casi e moltiplicando il risultato per 100.

1° esempio: a Lesina, durante gli anni compresi dal 2000 al 2005 sono nati 512 bambini. Di questi 252 sono maschi. Voglio calcolare la % di bambini maschi sul totale.
Riassumo così i dati:

Maschi + femmine	512
Maschi	256
Femmine	512 – 256

L’operazione da fare è la seguente:
256
---- = 0,4921 x 100 = 49,21 %
512
Quindi la percentuale di bambini maschi nati tra il 200 ed il 2005 è 49% (arrotondata), cioè 49 bambini maschi ogni 100 bambini nati. Di conseguenza, le femmine nate sono il 51% (100%–49%=51%).

2° esempio: Esaminiamo i gol fatti da un calciatore durante 5 anni di torneo di calcio. I dati sono riassunti nella tabella.

ANNO	NUMERO di GOL	FREQUENZA RELATIVA	FREQUENZA PERCENTUALE
2000	15	15/100 = 0.15	0.15 X 100 = 15%
2001	25	25 /100 = 0.25	0.25 X 100 = 25%
2002	30	30/100 = 0.30	0.30 X 100 = 30%
2003	20	20 /100 = 0.20	0.20 X 100 = 20%
2004	10	10/100 = 0.10	0.10 X 100 = 10%

Dall’esempio si nota come vengono calcolate le frequenze relative e percentuali dei gol realizzati nei 5 anni di torneo (N.B. 100 rappresenta il numero totale di gol fatti dal calciatore in 5 anni (cioè, 15+25+30+20+10=100).

Chi quadro
Una volta capito come si calcola una percentuale (%) possiamo applicare il test del Chi–quadro (per il cui calcolo provvede il computer).

1° esempio
Nelle scuole elementari e medie di Canicattì sono stati valutati i risultati dei promossi e respinti divisi per sesso durante l’anno 2005. La situazione viene esposta nella tabella sottostante.

STUDENTI	RESPINTI	PROMOSSI	TOTALE
Maschi	2	243	245
Femmine	7	225	233
Totale	9	468	477

L’ipotesi che scaturisce dalla lettura dei dati è la seguente: i maschi sono più bravi delle femmine in quanto solo lo 0.8% (2/243 * 100=0.8%) dei maschi è stato respinto, contro il 3.1% (7/225*100=3.1%) delle femmine.
L’ipotesi nulla, però, sostiene che non c’è differenza significativa tra maschi e femmine. Applichiamo, pertanto il chi-2. Immettendo i dati nel computer si ricava un valore di P = 0,077 (valore di significatività).
Poichè il valore calcolato di P è 0.077 e poiché esso è maggiore di 0.05 (P>0.05) à l’ipotesi nulla non può essere bocciata. Pertanto, si deve concludere che l’ipotesi secondo la quale i maschi siano più bravi delle femmine va respinta.

2° esempio
Nelle scuole superiori di Canicattì è stata valutata, su un campione di 100 studenti, la ricorrenza di influenza durante l’anno 2005, suddividendo gli studenti in due gruppi: quelli che vanno a scuola coi mezzi pubblici e quelli che vanno a scuola senza utilizzare i mezzi pubblici. La situazione viene esposta nella tabella sottostante.

STUDENTI	INFLUENZATI	NON INFLUENZATI	TOTALE
Usano mezzi pubblici	42	24	66
Non usano mezzi pubblici	12	22	34
Totale	62	38	100

L’ipotesi che scaturisce dalla lettura dei dati è la seguente: gli studenti che usano i mezzi pubblici si ammalano più facilmente di influenza in quanto ben il 63.6% (42/66 * 100=63.6%) degli studenti che usano i mezzi pubblici si è ammalato di influenza, contro il 35.3% (12/34*100=35.3%) degli studenti che non usano i mezzi pubblici.
L’ipotesi nulla, però, sostiene che non c’è differenza significativa tra i due gruppi di studenti. Applichiamo, pertanto il chi-2. Immettendo i dati nel computer si ricava un valore di P = 0,077 (valore di significatività).
Poichè il valore calcolato di P è 0.007 e poiché esso è minore di 0.05 (P<0.05 … anzi P<0.01) à l’ipotesi nulla è bocciata. Pertanto, si deve concludere che l’ipotesi secondo la quale gli studenti che usano i mezzi pubblici si ammalano più facilmente di influenza è vera.

Test di Fisher
E’ l’equivalente del Chi-quadro. Si usa, generalmente, quando il numero di casi misurati è piccolo (<20).

TEST U di MANN-WHITNEY e test di Wilcoxon
Entrambi i test servono per confrontare dati relativi a variabili ordinali. Una variabile è ordinale quando viene espressa con dei “numeri di ordine” che ne consentono, cioè, l’ordinazione crescente o decrescente (es. giudizio relativo ad un dolore: 0=assente, 1=lieve, 2=moderato, 3=intenso; oppure livello di intelligenza: 0=basso, 1=sufficiente, 2=normale, 3=elevato).
Il Test U di Mann-Whitney permette di confrontare i dati provenienti da due gruppi diversi, rispetto ad una variabile ordinale (es. valutare se il dolore provocato dalla puntura di una siringa è diverso tra Maschi e Femmine…in questo caso le misurazioni vengono effettuate su soggetti diversi).
Il Test di Wilcoxon permette di confrontare tra loro due misurazioni diverse di una variabile ordinale, fatte sugli stessi soggetti (es. valutare se il mal di testa in corso di influenza si riduce dopo assunzione di Tachipirina …in questo caso le misurazioni vengono effettuate 2 volte, prima e dopo l’assunzione del farmaco, sugli stessi soggetti).

Test di correlazione di spearman
E’ l’equivalente del Test di Correlazione di Pearson. Si usa, generalmente, quando le variabili sono ordinali (e non quantitative).

Appunti di statistica