variabili casuali

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

variabili casuali

SCHEDE SULLE VARIABILI CASUALI

Nozione

Variabile casuale (o aleatoria): insieme ordinato di valori numerici (che rappresentano un insieme delle risposte), ciascuno associato ad una probabilità; la somma delle probabilità dev’essere 1.

Le variabili casuali possono essere discrete, se i valori sono associabili a numeri naturali, o continue, se non lo sono (perché i valori sono “troppi” per poter essere contati).

Nel seguito si tratterà soltanto di variabili casuali discrete, che possono essere rappresentate in modo simile a quello usato per le distribuzioni di frequenza.

Esempio: qual è la variabile casuale per le risposte alla domanda: su 3 lanci di monete, qual è la probabilità che escano x teste?

L’insieme delle risposte, associato alle rispettive probabilità, è in questa tabella.

x: numero di teste in 3 lanci di monete	x₁ = 0	x₂ = 1	x₃ = 2	x₄ = 3
p: probabilità	p₁ = 1/8	p₂ = 3/8	p₃ = 3/8	p₄ = 1/8

La variabile casuale è data da tutti i valori possibili come risposta alla domanda, cioè 0, 1, 2 e 3.

Le probabilità sono ottenute calcolandole per ogni valore e usando la probabilità classica.

Tre lanci di monete danno 8 possibili risultati: 2 per il primo lancio, 2 per il secondo e 2 per il terzo, che vanno moltiplicati.

Esiste un solo modo di avere 0 teste ed è che in tutti i tre lanci sia uscita croce.

Esistono 3 modi di avere 1 testa, a seconda che la testa sia uscita al primo, al secondo o al terzo lancio.

Esistono 3 modi per avere 2 teste, a seconda che la croce sia uscita al primo, al secondo o al terzo lancio.

Esiste un solo modo di avere 3 teste ed è che in tutti i tre lanci sia uscita testa.

La tabella rappresenta una variabile casuale x discreta.

Si noti che la somma delle probabilità dà 1.

Esempio: se lancio due dadi con 6 facce, qual è la probabilità che la somma dei due esiti sia x?

L’insieme delle risposte, associato alle rispettive probabilità, è in questa tabella.

x	2	3	4	5	6	7	8	9	10	11	12
p	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

La variabile casuale è data da tutti i valori possibili come risposta alla domanda, cioè gli interi da 2 = 1+1 a 12 = 6+6.

Le probabilità sono ottenute calcolandole per ogni valore e usando la probabilità classica.

I possibili risultati sono 36: sono 6 per il primo dado e, per ciascuno di questi risultati, 6 per il secondo dado.

Esiste un solo modo di avere come risultato 2, cioè 1+1.

Allo stesso modo, esiste un solo modo di aver come risultato 12, cioè 6+6.

Esistono due modi per avere come risultato 3, cioè 1+2 e 2+1.

Allo stesso modo, esistono due modi per aver come risultato 11, cioè 5+6 e 6+5.

Esistono tre modi per avere come risultato 4, cioè 1+3, 2+2 e 3+1.

Allo stesso modo, esistono tre modi per aver come risultato 10, cioè 4+6, 5+5 e 6+4.

Continuando così, si arriva a trovare tutte le probabilità.

Si noti che la somma delle probabilità dà 1.

Funzione di ripartizione

Funzione di ripartizione: insieme ordinato di valori numerici (che rappresentano un insieme delle risposte), ciascuno associato alla somma delle probabilità dei valori minori o uguali ad esso.

Esempio: si vuole ottenere la funzione di ripartizione della seguente variabile casuale, calcolata sopra.

x: numero di teste in 3 lanci di monete	0	1	2	3
p: probabilità	1/8	3/8	3/8	1/8

La funzione di ripartizione è questa.

x: numero di teste in 3 lanci di monete	0	1	2	3
F(x): funzione di ripartizione	1/8	4/8 = 0,5	7/8	8/8 = 1

La funzione di ripartizione serve quindi a conoscere la probabilità che la variabile assuma valori minori o uguali ad un certo valore di x.

Valgono perciò le seguenti relazioni.

p(x£a) = F(a).

p(x<a) = F(a)-p(a).

p(x>a) = 1-F(a).

p(x³a) = 1-F(a)+p(a).

p(a<x£b) = F(b)-F(a).

È possible trovare altre varianti sul tema, come p(a<x<b), che si lasciano per esercizio.

Indici vari

Come per le distribuzioni di frequenza, anche per le variabili casuali si può calcolare moda, mediana, varie medie e scarto quadratico medio.

In genere, la media artitmetica, trattando di variabili casuali, viene chiamata valore atteso o speranza matematica. Si calcola usando le probabilità invece delle frequenze e, dato che il totale delle probabilità è 1, non serve dividere per esso.

Ecco un tipico uso del valore atteso: mi trovo davanti a due possibili eventi: il primo può capitare con una probabilità di 0,3 e dà un guadagno di 120 euro; il secondo può capitare con una probabilità di 0,7 e dà un guadagno di 100 euro. Qual è il guadagno medio M? Cioè, che guadagno mi aspetto?

Il ragionamento si può svolgere così: una probabilità frequentistica di 0,3 significa che in media, su 10 situazioni, in 3 capita l’evento; similmente per 0,7. Perciò, se considero 10 situazioni, il guadagno totale è 10M.

Il primo evento capita in media 3 volte, perciò il guadagno quando capita il primo evento è 3´120; similmente, quando capita il secondo evento il guadagno è 7´100. Il guadagno totale perciò è 3´120+7´100.

Confrontando i due diversi modi di scrivere il guadagno totale, si ha 10M = 3´120+7´100.

Isolando M, si ha M = (3´120+7´100)/10.

L’ultima uguaglianza si può scrivere anche come M = (3/10)´120+(7/10)´100.

In termini di probabilità frequentistica, si arriva a M = 0,3´120+0,7´100 (che, per la cronaca, fa 106).

Usiamo i simboli invece dei numeri; si ha che, avendo un evento con probabilità p₁ e guadagno x₁ e un altro evento con probabilità p₂ e guadagno x₂, bisogna trovare il guadagno medio (atteso) M.

Le probabilità, se trattate in senso frequentistico, possono essere scritte come p₁ = f₁/(f₁+f₂) e p₂ = f₂/(f₁+f₂).

Quindi ci sono f₁+f₂ casi totali, f₁ in cui capita il primo evento e f₂ in cui capita il secondo evento.

Il guadagno medio potrà essere trovato partendo da (f₁+f₂)M = f₁x₁+f₂x₂, che dà .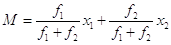

Tornando infine alle probabilità, si ottiene

M = p₁x₁+p₂x₂.

Naturalmente, gli stessi ragionamenti valgono anche con più di due eventi.

Può essere utile introdurre un nome per i prodotti p₁x₁, p₂x₂, p₃x₃, ..., p_nx_n. Chiamiamoli valori attesi parziali, dato che la loro somma è appunto il valore atteso (totale).

Esempio: si calcoli il valore atteso e lo scarto quadratico medio (con la formula ridotta) per la seguente variabile casuale, già usata sopra.

x: numero di teste in 3 lanci di monete	0	1	2	3
p: probabilità	1/8	3/8	3/8	1/8

Si ottiene questa tabella.

x	p	xp	x²p
0	0,125	0	0
1	0,375	0,375	0,375
2	0,375	0,75	1,5
3	0,125	0,375	1,125
somme = medie		1,5	3

Il valore atteso risulta M = 1,5; la varianza è VAR = 3-1,5² = 0,75; lo scarto quadratico medio è SQM = Ö0,75 = 0,866.

Giochi equi

Un gioco d’azzardo è equo se il valore atteso (totale) di ogni giocatore è nullo.

Esempio: dato che, per il decreto 179 del ministero dell’economia e delle finanze del 19 giugno 2003, art. 5, la posta dei concorsi a pronostici va al montepremi soltanto per il 34,65%, il totocalcio non è un gioco equo.

Infatti i giocatori, nel loro complesso, puntano una somma s e vincono una somma V = 0,3465s. Il valore atteso sarebbe perciò M = 0,3465ps-s = s(0,3465p-1), che è sempre negativo, perché p può al massimo valere 1.

La distribuzione geometrica

Le variabili casuali con un valido significato scientifico sono molte, ma nel seguito si tratterà soltanto di due.

La variabile casuale geometrica risponde alla domanda: faccio parecchi tentativi, i cui esiti sono fra loro indipendenti; per ciascuno dei tentativi ho una probabilità costante p di successo. Qual è la probabilità che il primo successo capiti al tentativo numero k?

Se il primo successo è il numero k, allora tutti gli k-1 precedenti tentativi sono fallimenti.

Se la probabilità di un successo è p, allora quella di un fallimento è 1-p.

Gli eventi, cioè i primi k-1 fallimenti e l’ultimo successo, devono capitare tutti, perciò vanno congiunti.

Gli esiti dei tentativi sono indipendenti, quindi, dato che vanno congiunti, le probabilità si possono moltiplicare.

Mettendo tutti questi ragionamenti insieme, si trova che per la variabile casuale geometrica G(k) vale la seguente regola di calcolo.

G(k) = (1-p)^k^-¹p.

Esempio: per un dato incontro, la probabilità che un venditore riesca a piazzare un prodotto è p = 0,2. Qual è la probabilità che il venditore piazzi il suo primo prodotto al quarto incontro?

Il venditore deve aver avuto un fallimento per 3 incontri e un successo al quarto, perciò è G(4) = (1-0,2)³0,2 = 0,1024.

Sicuramente G(k) rappresenta una probabilità; ma la successione delle G(k) serve a costruire una variabile casuale? La risposta è affermativa, grazie al seguente teorema.

Teorema: è SG(k) = 1.

Dimostrazione.

Rappresentiamo le formule in tabella.

k	1	2	3	...	¥
G(k)	(1-p)¹^-¹p = p	(1-p)p	(1-p)²p	...	(1-p)^¥^-1p = 0

Pertanto, bisogna calcolare la somma SG(k) = p+(1-p)p+(1-p)²p+(1-p)³p+...

Raccogliendo a fattor comune p e scrivendo per semplicità q invece di 1-p, si ottiene SG(k) = p(1+q+q²+q³+...).

In terza si è trovato il valore di 1+q+q²+q³+... per -1 < q < 1 (che è il nostro caso, perché q è una probabilità), cioè 1/(1-q).

(Chi volesse avere sottomano la dimostrazione, può guardare le SCHEDE DI MATEMATICA FINANZIARIA 2, al capitolo Le progressioni geometriche.)

Si arriva dunque a SG(k) = p/(1-q).

Dato che è stato posto sopra p = 1-q, è anche q = 1-p.

Perciò è SG(k) = 1.

CVD

Teorema: il valore atteso di una variabile casuale geometrica con probabilità p è 1/p.

Dimostrazione.

Si riprende la tabella sopra.

k	1	2	3	...	¥
G(k)	(1-p)¹^-¹p = p	(1-p)p	(1-p)²p	...	(1-p)^¥^-1p = 0

Tuttavia qui bisogna mostrare, ricordando che le probabilità qui si chiamano G(k), che è M = SkG(k) = 1/p.

Si cominci allora a scrivere SkG(k) = 1p+2(1-p)p+3(1-p)²p+... .

Raccogliendo a fattor comune p e scrivendo per semplicità q invece di 1-p, si arriva a SkG(k) = p(1+2q+3q²+...).

C’è un legame fra il generico addendo kq^k^-1 e q^k, che è l’addendo generico della serie q+q²+q³+...: quello è la derivata di questo rispetto a q.

La serie A = q+q²+q³+... è simile alla serie B = 1+q+q²+q³+...; l’unica differenza è il primo addendo. Perciò è A = B-1. Perciò è A = 1/(1-q)-1 = q/(1-q).

Per trovare una buona formula per 1+2q+3q²+..., bisogna allora derivare A rispetto a q, ottenendo A’ = 1/(1-q)².

Si arriva dunque a SkG(k) = p/(1-q)².

Dato che è stato posto sopra p = 1-q, è anche q = 1-p.

Perciò, semplificando, risulta M = SkG(k) = 1/p.

CVD

Con accorgimenti simili, ma qualche complicazione in più, si dimostra che la variabile casuale geometrica ha SQM = (1-p)^0,5p.

Esempio: trovare il valore atteso e lo scarto quadratico medio per l’esempio precedente.

Il venditore avrà il primo successo in media al tentativo numero 1/0,2 = 5, con uno scarto quadratico medio pari a (1-0,2)^0,50,2 = 0,1789.

La distribuzione binomiale

La variabile casuale binomiale risponde alla domanda: faccio parecchi tentativi, i cui esiti sono fra loro indipendenti; per ciascuno dei tentativi ho una probabilità costante p di successo. Qual è la probabilità di ottenere k successi su un totale di n tentativi?

La geometrica quindi è un caso particolare della binomiale: è come se nella binomiale fosse k = 1 e inoltre quest’unico successo dovesse capitare soltanto in una posizione ben precisa della successione (all’ultimo posto).

Se la probabilità di un successo è p, allora quella di un fallimento è 1-p.

Gli eventi, cioè i successi e i fallimenti, devono capitare tutti, perciò vanno congiunti.

Gli esiti dei tentativi sono indipendenti, quindi, dato che vanno congiunti, le probabilità si possono moltiplicare.

Se tutti i successi capitassero all’inizio della successione e tutti i fallimenti alla fine, la probabilità sarebbe p^k(1-p)ⁿ^-k.

Ma i successi possono benissimo essere sparpagliati sugli n tentativi, quindi ci sono molti più casi.

Per sapere quanti casi ci sono, serve il calcolo combinatorio: il mio insieme di origine è quello degli n tentativi; i miei insiemi destinazione sono quelli dei k successi. Non mi sto chiedendo quale successo è capitato per primo o per secondo o così via, perciò negli insiemi destinazione non conta l’ordine; non ha senso immaginare che un successo con un dato tentativo si ripeta (ogni tentativo esaurisce la possibilità di avere un dato successo), perciò negli insiemi destinazione non c’è ripetizione.

Abbiamo perciò a che fare con combinazioni senza ripetizione, il cui numero è .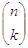

Mettendo tutti questi ragionamenti insieme, si trova che per la variabile casuale binomiale B(k) vale la seguente regola di calcolo.

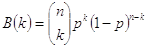Esempio: la probabilità che una ciliegia abbia un verme è 0,003. In un cestino di 40 ciliegie, qual è la probabilità di non trovare vermi? E di trovarne almeno 1?

La probabilità di non trovare vermi è k = 0, con p = 0,003 e n = 40.

La formula dà .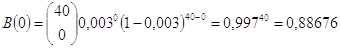

Trovare almeno un verme è negare di non trovare alcun verme, perciò la probabilità trovare almeno un verme è data da B(1, 2, ..., 40) = 1-0,88676 = 0,11324.

Sicuramente B(k) rappresenta una probabilità; ma la successione delle B(k) serve a costruire una variabile casuale? La risposta è affermativa, grazie al seguente teorema.

Teorema: è SB(k) = 1.

Dimostrazione.

Il coefficiente .

CVD

Ecco, senza dimostrazione, le formule per il valore atteso e lo scarto quadratico medio.

M = np;

SQM = Ö[np(1-p)].

Esempio: trovare il valore atteso e lo scarto quadratico medio per l’esempio precedente.

In un cestino in media ci sono 0,003´40 = 0,12 vermi, con uno scarto quadratico medio di 0,34589.

ESERCIZI SULLE VARIABILI CASUALI

V. C. GENERICHE

1) Scrivi la funzione di ripartizione della seguente variabile casuale, ricavando l’ultima probabilità:

x	2	3	4	5	6	7	8
p	0,1	0,3	0,2	0,15	0,05	0,02	...

2) Trova la variabile casuale delle risposte alla domanda: estraendo una pallina da un’urna che contiene 50 palline numerate da 1 a 50, qual è la probabilità che la cifra delle decine sia x?

3) Trova la variabile casuale delle risposte alla domanda: lanciando 2 dadi cubici, qual è la probabilità che la somma dei punteggi ottenuti con i due lanci sia x? Qual è la probabilità che la somma non sia maggiore di 4?

4) Trova la variabile casuale delle risposte alla domanda: lanciando 2 dadi cubici, qual è la probabilità che la differenza di punteggio fra il primo lancio e il secondo sia x? Qual è la probabilità che la somma sia compresa fra -1 e 2, estremi inclusi?

5) Trova la variabile casuale delle risposte alla domanda: lanciando 2 dadi cubici, qual è la probabilità che il valore assoluto della differenza di punteggio fra il primo lancio e il secondo sia x? Qual è la probabilità che questo valore non sia 0?

6) Trova la variabile casuale delle risposte alla domanda: estraendo 2 palline in blocco da un’urna che ne contiene 6 numerate da 1 a 6, qual è la probabilità che il maggiore dei due numeri estratti sia x? Qual è la probabilità che il maggiore sia almeno 4?

7) Trova il valore atteso e lo scarto quadratico medio di questa variabile casuale:

x	1	2	3	4	5
p	0,2	0,4	0,1	0,2	0,1

8) Trova la probabilità che rende equo il gioco rappresentato dalla seguente variabile casuale:

x	-3	-2	1	3
p	0,1	0,4	?	0,3

9) Trova il valore che rende equo il gioco rappresentato dalla seguente variabile casuale:

x	-2	0	?	3
p	0,4	0	0,5	0,1

V. C. GEOMETRICA

10) Le api pungono chi le disturba 1 volta su 30. Qual è la probabilità di disturbarle per 20 volte e di farla franca? Qual è il numero medio di volte che precedono la prima puntura? [0,017504]

11) Senza antivirus, ho una probabilità dello 0,1 di prenderne uno in ogni sito visitato. Quanti siti posso visitare prima che la probabilità cumulata di contagio sia 1/2? Qual è il numero medio di siti visitati fino al contagio? [6; 10]

12) In mensa fanno il brasato un giorno su sei. Qual è la probabilità che io mangi il brasato per la prima volta il quarto giorno? Quanti giorni devo aspettare in media per mangiare il brasato? [0,09645; 6]

13) La probabilità che in un dato mese una lampadina si fulmini è 0,08. Qual è la probabilità che si fulmini dopo un anno è mezzo? Qual è la durata media? [0,01939; 12,5]

14) In una certa specie, c’è una mutazione genetica in media ogni 400 generazioni. Qual è la probabilità che la prima mutazione genetica si abbia dopo 15 generazioni? Quanto si deve aspettare in media per avere una mutazione? [0,002457; 400]

15) In una certa città, la probabilità che un abitante abbia fatto un viaggio in Norvegia è 0,07. Qual è la probabilità che, intevistando a caso gli abitanti, se ne trovi uno che ha viaggiato in Norvegia soltanto al 10 tentativo? Quanti abitanti ci si aspetta di intervistare prima di trovarne uno che ha viaggiato in Norvegia? [0,03643; 14,29]

V. C. BINOMIALE

16) Dò un 4 ogni nove verifiche. Qual è la probabilità che correggendo i compiti in una classe di 25 studenti dia 3 volte 4? In media quanti 4 ci sono? [0,700151; 2,77778]

17) La probabilità che in una data seduta la borsa salga è 0,55; qual è la probabilità che salga in almeno 9 sedute su 15? In media quante salite ci sono? [0,45216; 8,25]

18) La probabilità che l’autobus sia in ritardo è 0,1. In 10 viaggi, qual è la probabilità di una maggioranza di ritardi? Quanti ritardi ci sono in media? [0,000147; 1]

19) La probabilità che un pezzo sia difettoso è 0,007. Qual è la probabilità che in un lotto di 1000 pezzi sia difettoso lo 0,4%? A buon senso, una percentuale difettosa del 2% avrà una probabilità grande o piccola? In media, quanti sono i pezzi difettosi nel lotto? [0,004951; 0,7]

20) La probabilità che un italiano preferisca l’olio al burro è 0,7. Su 100 italiani, qual è la probabilità che al massimo 10 preferiscano il burro all’olio? [0,0000...]

21) In media, in 4 locali su 10 servono birra annacquata. Su venti locali, qual è la probabilità di trovarne almeno 4 che servono birra annacquata? [0,05095]

22) Cinque studenti su 10 escono dalle medie con il giudizio di sufficienza. Qual è la probabilità che una classe di prima superiore di 25 studenti abbia almeno 15 studenti col giudizio di sufficienza? Quanti studenti con la sufficienza ci si aspettano? [0,88524; 12,5]

23) La probabilità di ricevere nei tempi prestabiliti un pacco ordinato negli USA è 0,4. Su 4 ordini, qual è la probabilità di riceverne nei tempi prestabiliti almeno la metà? In media, quanti ordini arrivano nei tempi prestabiliti? [0,1792; 1,6]

24) Un venditore ha successo in 2 casi su 10, Qual è la probabilità che in un giro di 20 incontri guadagni 2000 euro, se ogni provvigione è di 200 euro? Qual è il guadagno atteso? [0,03214; 800]

25) La probabilità che una malattia colpisca una persona è 0,2. In una comunità di 30 persone, qual è la probabilità che si ammalino più di 2 persone? Che non si ammali nessuna? Che se ne ammali un numero compreso fra 5 e 10, estremi inclusi? In media quante persone si ammalano? [0,98948; 0,001238; 0,71915; 6]

26) Trasformare i testi di questi esercizi in modo che la risposta corretta si applichi a una geometrica e non a una binomiale.

27) Se la probabilità che un congiurato mantenga il segreto sulla congiura è 0,99, qual è la probabilità che con 30 congiurati il segreto sia rivelato? [0,2603]

Fonte:

http://schedematematica.wikispaces.com/file/view/SCHEDE%20SULLA%20MATEMATICA%20ATTUARIALE.doc

http://schedematematica.wikispaces.com/file/view/ESERCIZI%20SULLE%20VARIABILI%20CASUALI.doc

Sito web da visitare :http://schedematematica.wikispaces.com/

Autore del testo: non indicato nel documento di origine

Parola chiave google : variabili casuali tipo file : doc

Matematica geometria ragioneria e statistica appunti esercizi lezioni riassunti testi materiale didattico

Matematica scuola elementare , scuola media, scuola superiore e università

Matematica geometria ragioneria e statistica appunti esercizi lezioni riassunti testi materiale didattico

variabili casuali