Elementi di Euclide

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Elementi di Euclide

GLI ELEMENTI DI EUCLIDE

Euclide(330 a.C.?-275a.C.?) è considerato il più famoso matematico di tutti i tempi. Nacque ad Alessandria e godette fama di scienziato puro, tutto preso dalle ricerche teoriche e dal culto del rigore; due aneddoti testimoniano il suo modo di vivere.

Al re Tolomeo che gli chiedeva se non ci fosse un metodo più semplice e più rapido di quello fondato sullo studio degli ELEMENTI, Euclide avrebbe risposto che non esistono "vie regie".

Un'altra volta un suo allievo gli avrebbe chiesto quali vantaggi fossero ricavabili dallo studio della geometria; pare che Euclide abbia ordinato ad un suo servo di dare a quel giovane una moneta e di scacciarlo, in quanto con la sua domanda si era dimostrato non solo venale ma anche incapace di comprendere il vero significato e l'inestimabile valore della scienza.

La popolarità di Euclide è dovuta alla sua maggiore opera: Gli ELEMENTI, un trattato che, per numero di edizioni e di traduzioni può competere con La Divina Commedia dantesca e, forse, è superato solo dalla Bibbia.

L'opera di Euclide rappresenta una sintesi organica delle conoscenze matematiche dei suoi tempi ed è ispirata a fini didattici: per molti anni è stato usato come testo nelle scuole, con ottimi risultati.

Il miglior testo euclideo è tuttora quello curato dal filosofo e matematico olandese J.L. Heiberg che fu uno dei più profondi conoscitori della matematica e della letteratura greca: è in greco con testo a fronte in latino. In italiano è da menzionare l'edizione curata da F. Enriques (in figura) e dai suoi collaboratori, che hanno tradotto l'intera opera euclidea.

Gli ELEMENTI si compongono di 13 libri, nei quali si trova esposta sistematicamente tutta la geometria elementare. Ogni libro inizia con un gruppo di proposizioni che possono essere considerate come una specie di definizioni che servono a chiarire i concetti successivi; esse sono seguite da altre proposizioni che sono invece veri e propri problemi o teoremi: questi si differenziano fra di loro per il modo con cui vengono enunciati e la frese rituale con cui si chiudono: "come dovevasi fare" per i problemi, "come dovevasi dimostrare" per i teoremi. I principi fondamentali esposti negli Elementi si distinguono in tre categorie: termini o definizioni, postulati (di natura geometrica) e nozioni comuni (postulati anch'essi, ma di

IL LIBRO 1

Il LIBRO I degli Elementi è il più poderoso ed in esso si trova praticamente tutta la geometria piana che si studia a scuola. Contiene 23 termini (pseudo-definizioni), 5 postulati e 5 nozioni comuni.

Vediamo alcuni "termini":

1) Punto è ciò che non ha parte

2) Linea è una lunghezza senza larghezza

.............

23) Parallele sono le rette di un piano che, prolungate da tutte e due le parti, da nessuna di esse si incontrano.

Ai termini del primo libro seguono nel testo originale i 5 postulati:

"Si ammette di poter condurre da qualsiasi punto ad ogni altro punto una linea retta ;"
"e che ogni retta terminata si possa prolungare continuamente per dritto;"
"e che con ogni centro e con ogni distanza si possa descrivere un circolo;"
"e che tutti gli angoli retti siano uguali tra di loro;"
"e che se una retta, incontrandone altri due, forma angoli interni da una stessa parte minori di due angoli retti, le due rette prolungate continuamente si incontrano dalla parte in cui sono gli angoli minori di due retti".

Il postulato n. 5, noto come IL QUINTO POSTULATO DI EUCLIDE o POSTULATO DELLE PARALLELE è quello caratteristico della geometria euclidea e da esso segue la dimostrazione dell'esistenza di almeno una parallela per un punto ad una retta data; da questo postulato e dalla proposizione 29 del libro 1 segue poi l'unicità della suddetta parallela.

Vediamo qualche sempio di "nozione comune":

1) Cose uguali ad una stessa cosa sono uguali;

2) il tutto è maggiore della parte;

.........

La prima proposizione di Euclide in cui si introduce il concetto di rette parallele, senza ancora ricorrere al quinto postulato, è la n. 27.

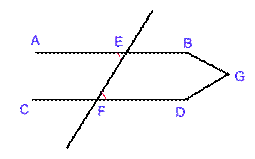
Se una retta, cadendo su due rette, fa gli angoli alterni interni uguali fra loro, le due rette saranno parallele fra loro.

Cadendo sulle due rette AB, CD, la retta EF formi gli angoli alterni AEF, EFD uguali fra loro. Dico che AB è parallela a CD.

Infatti se così non fosse, AB e CD prolungate (postulato 2) si incontrerebbero o dalla parte di B e D, o dalla parte di A e C.

Si prolunghino e si supponga che si incontrino nel punto G dalla parte di B e D. Allora, nel triangolo GEF, l'angolo esterno AEF risulterebbe uguale all'angolo interno ed opposto EFG, il che è impossibile (nella prop. 16 si dimostra il cosiddetto teorema dell'angolo esterno).

Dunque AB e CD, prolungate, non si incontrano dalla parte di B e D; analogamente si può dimostrare che esse non si incontrano neppure dalla parte di A e C. Ma allora, per il termine 23, le due rette sono parallele. Come dovevasi dimostrare.

Questo teorema rappresenta una vera vittoria sull'infinito, poichè il confronto di ciò che avviene al finito (l'uguaglianza tra due angoli) permette di dedurre una proprietà relativa ad un qualcosa che accade all'infinito.

Notiamo che le prime 27 proposizioni del primo libro degli Elementi non usano il suddetto Quinto postulato e pertanto sono vere anche nelle geometrie non euclidee. Ma il quinto postulato, lasciato accuratamente in disparte fino a questo momento, deve essere necessariamente utilizzato per invertire la prop. 27.

ENTRA IN GIOCO IL QUINTO POSTULATO

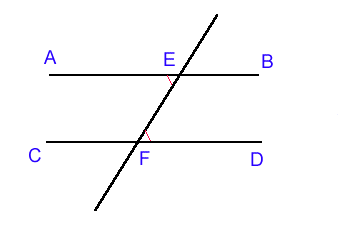
Una retta che cade su due rette parallele forma gli angoli alterni interni uguali fra loro, angoli corrispondenti uguali, angoli coniugati interni supplementari.

Vediamo come Euclide dinmostra la prima parte di questa proposizione:

"La retta EF cada sulle parallele AB e CD. Dico che essa forma gli angoli alterni interni AEF, EFD uguali fra loro.

Infatti; se gli angoli AEF ed EFD non fossero uguali fra loro, allora uno di essi sarebbe il maggiore. Sia AEF. Si aggiunga ad entrambi l'angolo BEF; allora gli angoli AEF e BEF presi insieme sono maggiori della somma degli angoli EFD e BEF (nozione comune 2). Ma gli angoli AEF e BEF presi insieme sono due angoli retti, dunque gli angoli EFD e BEF presi insieme sono minori di due angoli retti; ma allora per il postulato 5 le due rette AB e CD si intersecano dalla parte di B e D; ma esse non possono incontrarsi perchè sono parallele per ipotesi; ma allora l'angolo AEF non è disuguale all'angolo EFD e quindi è ad esso uguale. Come dovevasi dimostrare".

Questa teorema è la prima proposizione di "geometria euclidea" propriamente detta.

Il fatto che Euclide abbia tardato ad invocare il quinto postulato avvalora la congettura che già ai suoi tempi fossero sorte delle critiche intorno alla natura del postulato stesso. Di sicuro ai matematici che seguirono esso apparve meno evidente degli altri quattro, tanto che furono fatti diversi tentativi per dimostrarlo a partire dagli altri postulati, dalle nozioni comuni e dalle prime 28 proposizioni del Libro 1.

Questi tentativi si protrassero per venti secoli e condussero alla conclusione dell'impossibilità di dimostrarlo in base alle suddette premesse; anzi si dimostrò la possibilità logica di geometrie in cui esso non vale (Klein, Poincaré).

ALTRA FORMA DEL QUINTO POSTULATO

Prima di addentrarci nelle dispute intorno al quinto postulato domostriamo l'equivalenza tra la forma data da Euclide e quella (forse più nota) secondo cui:

postulato 5': "Per un punto esterno ad una retta passa una sola parallela ad una retta data".

Ricordiamo che l'esistenza di una parallela ad una retta data per un punto ad essa esterno viene dimostrata da Euclide nella proposizione 31 (si costruiscono due angoli alterni interni uguali....).

Con la proposizione 30 si dimostra la cosiddetta proprietà comparativa del parallelismo, ovvero che: "le parallele ad una stessa retta sono parallele fra loro" ( per la dimostrazione si sfrutta il fatto che due rette parallele formano con una trasversale angoli alterni interni uguali e viceversa).

Dimostriamo che da postulato 5 segue il postulato 5':

se per un punto P esterno ad una retta a passassero due rette parallele ad a queste dovrebbero essere tra di loro parallele ( in base alla prop. 30); ma avendo un punto in comune, P, sono coincidenti.

Dimostriamo che dal postulato 5' segue il postulato 5:

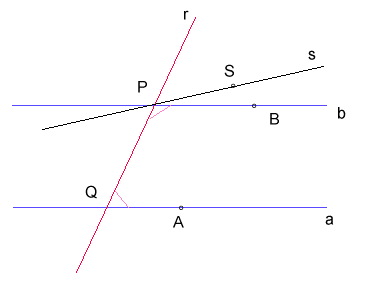
Supponiamo che le due rette siano parallele; esiste per P una retta s tale che insieme ad a e alla trasversale r forma angoli coniugati interni supplementari; ma allora, per la prop. 28 (dimostrata, ricordiamolo, senza ricorrere al quinto postulato) segue che s è parallela ad a; ma anche b è parallela ad a e pertanto, per il postulato 5' s deve coincidere con b; ma allora a e b formano con la trasversale r angoli coniugati interni la cui somma è due angoli retti, mentre per ipotesi la loro somma è minore di due angoli retti; allora non può essere b parallela ad a e quindi ne segue la tesi.

COME ARRIVA EUCLIDE AL QUINTO POSTULATO?

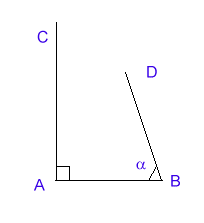
L'enunciato di Euclide è solo più generale di questo; infatti si parla di due angoli la cui somma sia minore di due angoli retti.

LE DISPUTE INTORNO AL QUINTO POSTULATO

Le dispute intorno al Quinto postulato si possono dividere in tre fasi:

PRIMA FASE: si cerca di ridefinire il postulato in questione (Tolomeo, Posidonio e Gemino, Proclo), ma si arriva alla sua sostituzione, più o meno esplicita, con uno equivalente.

SECONDA FASE: si cerca di dimostrare il quinto postulato (dal 1500 in poi), ma si giunge solo ad un postulato ad esso equivalente. La presenza del quinto postulato senza dimostrazione sembrava un difetto gravissimo degli Elementi; era assolutamente necessario liberare, emendare, purificare l'opera di Euclide da tale macchia, da tale neo; significativo a tal riguardo il titolo dell'opera di Gerolamo Saccheri: Euclides ab omni naevo vindicatus.

TERZA FASE: ci si convince dell'impossibiltà di dimostrare il quinto postulato e si costruiscono le prime geometrie non euclidee.

La prima idea nuova nel tentaivo di dimostrare il quinto postulato si ha nel 1663 con J. Wallis (in figura) , ma il tentativo meglio strutturato fu quello di di P.G. Saccheri (Sanremo 1667-Milano 1773) che arrivò ad un passo dalla scoperta delle geometrie non euclidee.

IL TENTATIVO DI P. SACCHERI

Il gesuita italiano pensò di dimostrare il quinto postulato a contrariis: sia questo postulato ciò che bisogna dimostrare; si assuma a punto di partenza la negazione di esso; se questa negazione, nel corso del procedimento dimostrativo, si distrugge da sé, essa risulterà falsa e quindi il postulato, che costituisce il suo contrario, risulterà vero.

Sta di fatto che egli pose a punto di partenza due ipotesi negative del quinto postulato che "dimostrò" inconsistenti solo perché non coerenti con l'impianto sistematico della stessa geometria euclidea. Ma quelle due ipotesi suggerirono ai matematici dell'Ottocento la via per dimostrare non solo che il quinto postulato era indimostrabile, ma che era possibile costruire su di esse delle nuove geometrie "non euclidee".

Seguiamo, a grandi linee, il ragionamento che Saccheri ha esposto nell'opera "Euclide emendato da ogni macchia" (Euclides ab omni naevo vindicatus).

Sia un segmento AB; dagli estremi si elevino due segmenti perpendicolari di uguale grandezza tra loro, AC e BD; si congiunga C con D. Gli angoli alfa e beta sono uguali e retti; si verifica facilmente che anche gli angoli gamma e delta saranno anch'essi uguali tra loro (basta considerare le coppie di triangoli congruenti ABC e ABD e successivamente la coppia di triangoli ADC e ACB che risultano anch'essi congruenti).

Ma tali angoli saranno anche retti?

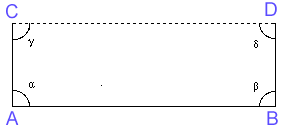
Secondo il postulato di Euclide, sí (prima ipotesi). Assumiamo ora le due ipotesi opposte a quel postulato: cioè quella per cui essi sono entrambi ottusi (seconda ipotesi), e quella per cui sono entrambi acuti (terza ipotesi). Nell'ipotesi dell'angolo ottuso, gli angoli gamma e delta saranno ognuno maggiore di un angolo retto; nell'ipotesi dell'angolo acuto, essi saranno entrambi minori di un angolo retto. È chiaro che se si assume l'ipotesi dell'angolo retto, allora vale la conclusione che la somma degli angoli interni di un triangolo è uguale a due angoli retti; ma se si assume quella dell'angolo ottuso, essa sarà sempre maggiore di due retti, e se si ammette quella dell'angolo acuto, essa sarà sempre minore di due retti.

Si esamini dunque la validità della seconda ipotesi; il quinto postulato non è per sé incompatibile con essa; allora dovrebbero valere anche i teoremi connessi a quel postulato; tra questi c'è quello per cui la somma degli angoli di un quadrilatero è uguale a quattro retti; ma nell'ipotesi dell'angolo ottuso la somma degli angoli del quadrilatero sarà di necessità maggiore di quattro retti; allora la seconda ipotesi si distrugge da sé e decade.

In realtà tale ipotesi non era decaduta, perché Saccheri non ha dimostrato incoerenza tra conseguenze e premesse assunte in via ipotetica, ma solo l'incompatibilità tra l'ipotesi ammessa e le conseguenze connesse all'ipotesi euclidea.

Saccheri poi dimostra l'insostenibilità dell'ipotesi dell'angolo acuto, ma commette un errore, in quanto estende all'infinito una proprietà che è valida al finito (per un punto esterno ad una retta si può tracciare una sola perpendicolare ad una retta data).

DOPO P. SACCHERI

Con le ipotesi dell'angolo ottuso e dell'angolo acuto lo stesso Saccheri aveva gettato le basi dei due tipi di geometrie non euclidee, che saranno definite rispettivamente, dai nomi dei loro elaboratori, geometria di Riemann e geometria di Lobacevskij.

Ma già prima di questi due matematici, LUIGI LAGRANGE (1736-1813) intuí la possibilità di ricavare geometrie "diverse" da quella euclidea; solo che egli, vittima del pregiudizio comune, non osò comunicare i suoi risultati, perché avrebbe dovuto sostenere pubblicamente che ci sono piú geometrie "vere", il che gli sembrava scandaloso. Bisognava arrivare alla consapevolezza che non esiste una geometria "vera", ma che ogni geometria è "vera" se non contraddittoria, nei procedimenti e nei risultati, con l'ipotesi assunta. Ma questa consapevolezza non poteva essere una conquista indolore, se si pensa che ammettere una geometria non euclidea significava abbandonare la stessa nozione di spazio tridimensionale che sta alla base del sistema euclideo, e per la quale quel sistema è incondizionatamente valido; e significava abbandonare, con quella nozione di spazio, anche la nozione euclidea di piano, di retta, ecc. (ad esempio, se disegnati su una superficie sferica, la retta sarà anche un arco di circonferenza, il quadrilatero fondamentale isoscele avrà angoli interni che sommati saranno maggiori di quattro retti, e il triangolo avrà angoli interni che sommati saranno maggiori di due retti). La resistenza ad ammettere "altre" geometrie veniva proprio dall'idea che lo spazio "reale" fosse quello "euclideo", e pertanto quella euclidea fosse l'unica vera geometria.

In ogni caso, nella prima metà dell'Ottocento venne ripreso il discorso di Saccheri. E nacque quella che oggi si dice "geometria iperbolica", per la quale, assunta l'ipotesi dell'angolo acuto, per un punto esterno ad una retta complanare si possono condurre non una ma due parallele alla retta data. E solo nella seconda metà dell'Ottocento fu scoperta quella "geometria ellittica" costruita sull'ipotesi dell'angolo ottuso, e per la quale per un punto esterno e complanare ad una retta non passa alcuna parallela alla retta data.

IL CONTRIBUTO DI GAUSS

KARL FRIEDRICH GAUSS (1777-1855) è considerato il primo matematico giunto alla precisa e chiara concezione di una geometria indipendente dal quinto postulato, ma egli non pubblicò i risultati raggiunti, per non suscitare le proteste e le risa di coloro che non sarebbero stati in grado di valuatare tale scoperta, per timore degli "strilli dei beoti". Sembra che Gauss abbia scritto a Bolyai padre (Farkas, in figura a sinistra),

per comunicare i suoi risultati; quest'ultimo pare sia impazzito nello studio del quinto postulato, di cui aveva intuito l'indipendenza dai primi quattro postulati, a tal punto da imporre per testamento al figlio Janos di non occuparsi di tale problema; ma il figlio arrivò alla costruzione di una nuova geometria non cercando di dimostrare il quinto postulato ma negandone la validità.

Dopo un iniaziale tentativo di dimostrare il quinto postulato, Gauss arriva (1831) gradualmente alla convinzione che esiste una geometria che nulla ha in sè di contraddittorio. Ma, a causa della discrezione con cui Gauss mosse questi primi, seppur tanto sicuri passi su un terreno così pericoloso e ignoto, tutto l'onore della scoperta venne tributato poco dopo a due matematici più che giovani che, all'insaputa uno dell'altro ed in lontani paesi, giunsero quasi contemporaneamente ad analoghi risultati: l'ungherese Janos Bolyai (Kolosvàr 1802-Marosvàsàrhely 1860) ed il russo Nicolaj Ivanovic Lobacevskij (Makarèv 1793-Kazan' 1856), detto "il Copernico della geometria" perchè come Copernico riuscì con la sua teoria eliocentrica del sistema planetario a far cadere una teoria (quella geocentrica di Tolomeo) che durava da diversi secoli, così egli riusci a far cadere una teoria (la geometria euclidea) che per duemila anni era stata considerata l'unica possibile.

Si mise in crisi cosí la certezza che la geometria euclidea fosse l'unica ad avere validità sia sul piano dell'esperienza ordinaria, sia sul piano logico; infatti del quinto postulato, valido per l'esperienza ordinaria, si può fare a meno sul piano logico. E su questa convinzione poggiano le costruzioni di Bolyai e di Lobacevskij.

Bolyai e Lobacevskij


Janos Bolyai	Nicolaj Ivanovic Lobacevskij

Il procedimento seguito dai due matematici (con molta approssimazione espositiva) è il seguente.

Dati una retta AB e un punto P complanare ed esterno ad essa, sia PO la perpendicolare alla retta passante per il punto P. Si consideri ora un punto D sulla retta AB; per esso passerà la retta PD secante la retta data. Si faccia muovere il punto D nel verso OB in corrispondenza di ogni posizione occupata da D sulla retta, si otterrà una secante PD alla retta assegnata. Si consideri ora la distanza OD tendente all'infinito; troveremo in corrispondenza una retta PL che non intersecherà la retta AB, e che quindi sarà parallela ad OB.

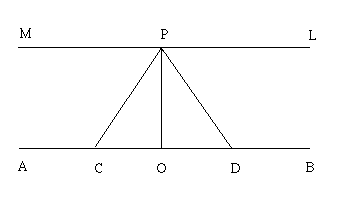
Si proceda in ugual modo dall'altra banda; anche in questo caso si troverà una retta PM non secante la retta data, e pertanto parallela ad OA.

Ora, secondo la geometria euclidea, PL e PM costituiscono un'unica retta parallela ad AB, e gli angoli OPL e OPM sono uguali e retti. Si assuma invece l'ipotesi dell'angolo acuto; allora PL e PM saranno due rette distinte, ed entrambe parallele ad AB pur senza essere equidistanti in ogni punto rispetto alla retta data! Quali sono le condizioni del loro parallelismo? Anzitutto bisognerà distinguere per ognuna delle due rette un proprio verso di parallelismo: e si dirà che PL è parallela ad OB e PM è parallela ad OA; inoltre ognuna di esse, pur prolungata all'infinito nel verso del parallelismo, non incontrerà mai la retta data, e la distanza da questa diminuirà infinitamente.

Da questa nozione di parallelismo discendono poi una serie di proprietà matematicamente dimostrabili. Ad esempio che l'angolo di parallelismo pigreco (OPL + OPM) è variabile in dipendenza dalla grandezza della perpendicolare PO; cioè diminuisce con l'aumentare della perpendicolare, e aumenta col diminuire della perpendicolare; perciò esso tende a zero quando la perpendicolare tende all'infinito; e tende a pigreco quando la perpendicolare tende a zero.

Inoltre, la distanza tra due rette parallele, ad esempio PL e OB, tende a zero nel verso del parallelismo, e invece tende all'infinito nel verso opposto.

Infine due rette parallele tra loro non avranno alcuna perpendicolare in comune; o meglio la avranno all'infinito, cioè là dove esse formano un angolo nullo.

Con ciò fu dimostrato che è possibile costruire un sistema geometrico logicamente coerente e rigoroso, a partire da una ipotesi prescelta, e che non solo non si dava un'unica geometria vera, quella euclidea, ma questa era anch'essa una costruzione basata su un'ipotesi preliminarmente scelta.

Bernhard Riemann

A confermare che era possibile costruire geometrie diverse da quella euclidea fu Bernhard Riemann (1826-1866), che costruí un altro tipo di geometria, egualmente rigorosa e coerente, ipotizzando una nozione di spazio, di piano, di retta ecc. diversa da quella che era alla base del sistema euclideo. Ciò fece nel suo celebre saggio Sulle ipotesi che stanno alla base della geometria, del 1854.

È un errore, dice Riemann, confondere l'"illimitatezza" con l'"infinità" dello spazio; il primo concetto è infatti relativo all'"estensione", cioè è un concetto "qualitativo"; il secondo invece è relativo alla "misura", cioè è un concetto "quantitativo". Sicché si può ipotizzare uno spazio che sia insieme "illimitato" e "finito"; e quindi una retta che sia, ugualmente, illimitata e finita. Nel caso della retta, essa risulterà quindi "chiusa".

Allora, si consideri in un unico piano una retta e un punto fuori di essa. Si assuma la retta illimitata e finita. Si consideri di essa, ora, un qualsiasi punto N; esso, spostandosi, ritornerà al punto di partenza avendo percorso una distanza di misura finita.

Orbene, già si può constatare che in uno stesso piano due rette s'incontrano sempre e necessariamente, in qualunque condizione le si consideri; ossia che due rette, in uno stesso piano, non possono essere parallele tra loro, secondo la definizione euclidea di parallelismo. Ma si considerino le perpendicolari ad una retta qualunque, sussistenti da una stessa banda. Esse, tutte, passeranno per uno stesso punto A. Inoltre questo unico punto A risulterà equidistante da tutti i punti della retta data. Prendiamo ora in esame tutte le perpendicolari a quella retta dalla parte opposta. Anche in tal caso esse si incontreranno in uno stesso punto A' equidistante da ciascun punto della retta data.

Ora si possono dare due casi diversi: il primo, in cui il punto A e il punto A' coincidono; il secondo, in cui detti punti non coincidono. Nel primo caso avremo una "geometria ellittica", nel secondo una "geometria sferica". Nel primo caso due rette s'incontrano in un solo punto; nel secondo due rette s'incontrano sempre in due punti.

LA SOMMA DEGLI ANGOLI INTERNI DI UN TRIANGOLO

Quanto al teorema euclideo in base al quale la somma degli angoli interni di un triangolo è uguale a due retti, nelle geometrie non euclidee, per la diversa nozione di piano che ne sta alla base, esso viene modificato in questi termini. Per la geometria di Riemann quella somma è sempre maggiore di due retti; per quella di Lobacevskij essa è sempre minore di due retti.

La cosa non risulterà difficile se si considera un triangolo una volta disegnato su una superficie sferica (geometria di Riemann) e una volta disegnato sulla superficie esterna di una trombetta (secondo il modello della geometria di Lobacevskij); in entrambi i casi avremo un triangolo con lati curvilinei. Ma c'è di piú. A partire dall'ipotesi di Riemann si dimostra che c'è una differenza tra la somma degli angoli interni e due retti, che è definita "eccesso angolare", e che aumenta con l'ingrandirsi del triangolo. Se invece si considera il modello della geometria di Lobacevskij, esiste una differenza tra due retti e la somma degli angoli interni di un triangolo, che vien definita "difetto angolare", e che aumenta con l'ingrandirsi del triangolo.

IL MODELLO DI FELIX KLEIN (1849-1925)

In tale modello si fissa una conica K irriducibile (per comodità un'ellisse o una circonferenza) e si danno le seguenti interpretazioni dei concetti primitivi:

punto è un punto interno a K;
retta è una corda di K estremi esclusi;
piano è l'insieme dei punti interni di K.

Si costruisce un modello di geometria che soddisfa tutti gli assiomi della geometria euclidea (in una forma più moderna data da Hilbert) tranne il quinto e per la quale valgono le prime 28 proposizioni del I libro degli Elementi: il quinto postulato è quindi indimostrabile a partire dai primi quattro postulati e dalle prime 28 proposizioni, quindi è indipendente da essi; una geometria basata sui primi quattro postulati e sulle prime 28 proposizioni non presenta alcuna contraddizione logica.

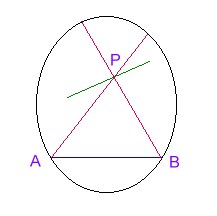
Le due rette PA e PB dividono le rette che intersecano la retta AB da quelle che non la intersecano; vi son perciò infinite rette passanti per P parallele ad AB; seguendo la dfinizione di Hilbert si chiamano però parallele le rette PA e PB, le "separatrici" delle rette parallele da quelle non parallele.

Pertanto:

"Per un punto esterno ad una retta passano due rette parallele alla retta data".

La geometria non euclidea in cui vale il precedente postulato al posto del quinto di Euclide è detta "geometria iperbolica".

N.B. Un altro modello di geometria iperbolica viene sviluppato da Poincarè: in tale modello si fissa una circonferenza K; si chiama punto un punto interno alla circonferenza; si chiama retta l'insieme dei punti di una circonferenza perpendicolare a K che sono interni a K.

UN MODELLO DI GEOMETRIA NON EUCLIDEA ELLITTICA

In tale geometria il quinto postulato di Euclide viene sostituito dal seguente:

"Due rette hanno sempre un punto in comune"

Come dire che per un punto esterno ad una retta non passa alcuna retta parallela alla retta data.

Un modello di tale geometria si ha nella cosiddetta "geometria della sfera". In tale modello si fissa una sfera S e si definiscono nel modo seguente gli enti fondamentali:

punto è una coppia di punti di S diametralmente opposti;
retta è una circonferenza massima di S.

E' evidente che due rette cosiffatte si intersecano sempre in un punto (una coppia di punti della sfera diametralmente opposti).

Fonte: http://www.alessandrobonini.it/download/matematica/GLI%20ELEMENTI%20DI%20EUCLIDE%20E%20ALTRO...doc

Autore del testo: non indicato nel documento di origine

Sito web : http://www.alessandrobonini.it/

Parola chiave google : Elementi di Euclide tipo file : doc

Gli Elementi di Euclide

Libro VII

Definizioni

Unità è ciò secondo cui ciascun ente è detto uno.
Numero è una pluralità composta da unità.
Un numero è “parte” di un [altro] numero, il minore di quello maggiore, quando esso misuri il maggiore (= lo divida).
È “parti”, invece, di un numero, quando non lo misuri.
Un numero maggiore è multiplo di un numero minore, quando sia misurato dal minore.
Numero pari è quello che è divisibile in due parti (=numeri) uguali.
Numero dispari è quello che non è divisibile in due parti uguali, ossia quello che differisce di un’unità da un numero pari.
Numero parimente pari è quello che è misurato da un numero pari secondo un numero pari (= è divisibile per quattro).
Numero parimente dispari è quello che è misurato da un numero pari secondo un numero dispari (= è divisibile per due, ma non per quattro).
Numero disparimente dispari è quello che è misurato da un numero dispari secondo un numero dispari (= è prodotto di due numeri dispari).
Numero primo è quello che è misurato soltanto dall’unità.
Numeri primi fra loro sono quelli che hanno soltanto l’unità come misura (=divisore) comune.
Numero composto è quello che è misurato da un qualche numero.
Numeri composti fra loro sono quelli che hanno un qualche numero come misura comune.
Si dice che un primo numero moltiplica un secondo numero, quando si ottenga un terzo numero componendolo con la somma di tante volte il secondo per quante sono le unità del primo.
Quando due numeri, moltiplicandosi fra loro, producano un terzo numero, il prodotto si chiama numero piano, ed i numeri che si moltiplicano fra loro si chiamano i suoi “lati”.
Quando tre numeri, moltiplicandosi fra loro, producano un quarto numero, il prodotto si chiama numero solido, ed i numeri che si moltiplicano fra loro si chiamano i suoi “lati”.
Numero quadrato è quello che è prodotto di due numeri uguali, ossia è un numero piano che ha per lati due numeri uguali.
[Numero] cubo è quello che è prodotto di tre numeri uguali, ossia è un numero solido che ha per lati tre numeri uguali.
[Quattro] numeri sono in proporzione quando, a seconda che il primo sia multiplo, sottomultiplo, o una frazione qualunque del secondo numero, corrispondentemente il terzo sia lo stesso multiplo, o lo stesso sottomultiplo, o la stessa frazione del quarto.
Numeri piani e solidi simili [fra loro] sono quelli che hanno i lati proporzionali.
Numero perfetto è quello che è uguale alla somma delle proprie parti (=dei suoi divisori).

Si noti che, come emerge chiaramente dalle Definizioni XIII e XIV, il numero è per Euclide sempre un numero intero positivo diverso da uno, il divisore (la “parte”) è sempre non banale. Sulla distinzione tra “uno” e “numero” si veda un commento di Pascal.

Il concetto di numero piano della Definizione XVI richiama alla memoria l’usanza pitagorica di rappresentare i numeri come sassolini disposti su righe e colonne. Il numero piano è un particolare numero poligonale, avente la forma di un rettangolo:

I “lati”corrispondono a due fattori in cui il numero – il 24 - si decompone: nell’esempio sono 4 e 6. Se i due lati sono uguali, il rettangolo è un quadrato, ed il numero è il prodotto di due fattori uguali, cioè è quadrato nel senso della Definizione XVIII.

Le nozioni di numero solido e di numero cubo (Definizioni XVII e XIX)

sono le estensioni tridimensionali delle precedenti.

La figura rappresenta il numero solido 3´4´6 = 72.

Due numeri piani simili ai sensi della Definizione XXI sono rappresentati da rettangoli simili: i lati dell’uno si ottengono moltiplicando i lati del secondo per lo stesso numero, che nell’esempio raffigurato è il 2:

Il secondo numero sarà dunque ottenuto dal primo moltiplicandolo per un numero quadrato, nel nostro caso il 4 (Libro VIII, Proposizione 26).

Analogamente, dati due numeri cubi simili, uno sarà ottenuto dall’altro moltiplicandolo per un numero cubo (Libro VIII, Proposizione 27).

Come Euclide dimostra nel Libro IX, due numeri sono numeri piani simili se e solo se il loro prodotto è un numero quadrato (Proposizioni 1 e 2). Attenzione: non vale il risultato analogo per i numeri solidi!

A Pitagora risale anche la nozione di numero perfetto.

A questo breve dizionario aritmetico si ispirerà, nel 1700, G.A. Alberti.

Fonte: http://www.dm.uniba.it/ipertesto/euclide/definizioni7.doc

Autore del testo: non indicato nel documento di origine

Parola chiave google : Elementi di Euclide tipo file : doc

Matematica geometria ragioneria e statistica appunti esercizi lezioni riassunti testi materiale didattico

Matematica scuola elementare , scuola media, scuola superiore e università

Matematica geometria ragioneria e statistica appunti esercizi lezioni riassunti testi materiale didattico

Elementi di Euclide