Radicali esponenti frazionari e potenze

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Radicali esponenti frazionari e potenze

Scheda sui radicali e gli esponenti frazionari

Richiami: proprietà delle potenze

La formula aⁿ indica che si moltiplica a per n volte. Si ricorda che a è chiamato base, n è chiamato esponente e l’intera operazione è chiamata potenza.

Valgono le seguenti proprietà, dove a e b possono essere numeri di ogni genere noto ad uno studente di seconda (numeri interi, relativi, decimali, frazioni), mentre, in questo paragrafo, n e m possono essere soltanto numeri interi (positivi o negativi).

a¹ = a.

a⁰ = 1, tranne quando è a = 0; in questo caso, la formula non ha un valore evidente.

0ⁿ = 0, tranne nel caso in cui è n = 0, come sopra.

1ⁿ = 1.

aⁿ´a^m = aⁿ^+m.

aⁿ : a^m = aⁿ^-^m.

(aⁿ)^m = a^nm.

aⁿ´bⁿ = (ab)ⁿ.

a^-ⁿ = (1/a)ⁿ = 1/aⁿ.

(a/b)^-ⁿ = (b/a)ⁿ.

QUESTE PROPRIETÀ VANNO SAPUTE A MENADITO ALMENO FINO ALL’ESAME DI STATO. Anche perché saranno usate in terza, in quarta e in quinta.

Nozione di radice

Notazione classica

Come la sottrazione è l’operazione inversa all’addizione e la divisione è quella inversa alla moltiplicazione, così la radice è l’operazione inversa alla potenza.

Quindi .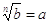

Il simbolo 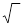è il classico simbolo di radice; in generale, bisogna stabilire qual è il suo indice, cioè il numero n che va posto sopra a sinistra. Il numero n può assumere tutti i valori interi; vanno notati in particolare i casi che seguono:

* per convenzione mondiale, quando n vale 2 non lo si scrive, perciò si ha

;

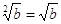* inoltre, quando n vale 1, si sta facendo l’inverso di una potenza con esponente 1, cioè non si sta facendo niente; perciò si ha

;

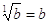* infine, in generale non si riesce a dare un significato alla radice con n che vale 0; perciò si ha

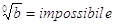Motivo di quest’ultimo fatto: essendo la radice l’inverso della potenza, da 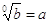. Ma il membro a destra vale 1, perciò deve valere 1 anche quello a sinistra.

La notazione sopra è quella classica dei libri di testo, che procedono in un modo didatticamente stravagante: prima, in seconda, riempiono le pagine di formule piene di 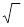, contribuendo a parecchi mal di testa, poi sul finire dell’argomento... ops! Rivelano, quasi fra le righe, che c’è un altro modo di fare i conti con le radici, cioè le potenze con esponente frazionario. In terza, bisogna imparare tutto di nuovo, pensando appunto agli esponenti frazionari invece che al classico simbolo di radice.

Notazione esponenziale

Qui si decide di procedere in modo semplice e diretto, perciò la definizione di radice verrà subito data in forma di esponenti, così:

la formula .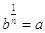

L’ultima frase scritta è la definizione di radice, scritta nel modo più pratico e comodo, ed è il punto fondamentale da sapere studiando le radici, perché tutto parte da lì.

Quindi la potenza b^1/n, in cui l’esponente è una frazione, è esattamente la radice ennesima di b.

Esempio: è .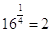

In particolare, se l’esponente è 1/2 si sta facendo una radice quadrata, mentre se è 1/3 si sta facendo una radice cubica.

Nella formula 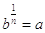, le lettere hanno un nome:

* b (che può rappresentare non soltanto un numero, ma anche un’intera espressione) viene chiamato radicando;

* n (che di solito sarà un numero, ma non è un obbligo) si chiama indice (o grado) della radice;

* a, cioè il risultato dell’intera operazione, si chiama radicale e può anch’esso rappresentare un’intera espressione.

Per essere espliciti: l’elevamento all’esponente 1/n si chiama radice, mentre l’intera potenza b^1/n viene chiamato nei libri radicale. Nel seguito, con grande costernazione per i notai della matematica, si userà ‘radice’ per intendere sia le radici sia i radicali; tanto non c’è pericolo di confusione.

Perché l’esponente frazionario è la radice?

L’idea di stabilire che un esponente frazionario è una radice sembra del tutto arbitraria; mostriamo ora che invece funziona benissimo. Una radice è essenzialmente l’inverso di una potenza. Il suo ruolo è quello. Basta mostrare che l’esponente frazionario svolge lo stesso ruolo e il suo uso viene giustificato.

Si parte da .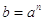

Dato che stiamo trattando dell’inverso della potenza, troviamo il modo di invertire questa formula, stabilendo anzitutto che cosa si intende per inversione: questa formula è invertita quando a resta da solo a destra dell’uguale ed ogni complicazione formale passa a sinistra dell’uguale, agendo su b.

In sintesi, mostriamo il seguente teorema: se la proprietà (aⁿ)^m = a^nm vale anche per esponenti frazionari, allora le potenze con esponenti frazionari (cioè le radici) invertono le potenze con esponenti interi (cioè le potenze per eccellenza).

In effetti non è dimostrato perché la proprietà (aⁿ)^m = a^nm dovrebbe valere anche per gli esponenti in forma di frazione; questo aspetto viene semplicemente preso come una proprietà iniziale, necessaria a fare tornare i conti; d’altronde, si tratta di una proprietà del tutto accettabile sul piano intuitivo.

Primo: eleviamo a sinistra e a destra dell’uguale per 1/n; si ottiene

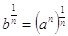Secondo: a destra applichiamo la proprietà delle potenze che toglie le parentesi fra gli esponenti, secondo cui (aⁿ)^m = a^nm. Con questa proprietà, si ottiene

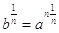Naturalmente, è 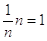, perciò si ottiene

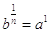Dato che è a¹ = a, si arriva a

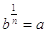Ecco che la formula è stata invertita: da 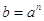, perciò da una potenza si ottenuta la formula inversa e tale formula inversa è appunto ciò che si intende per radice.

Calcolo concreto di una radice

Le radici di indice qualunque si calcolano concretamente usando le calcolatrici scientifiche (contenute anche in alcuni modelli di telefonino), ma si può anche calcolarle a mano; ecco un metodo efficiente (per sapere perché questo metodo funziona, bisogna aspettare almeno di aver svolto il programma di quarta).

Se si vuole trovare quanto fa 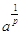, bisogna svolgere una serie di calcoli, ciascuno dei quali dà un certo risultato, che è sempre più vicino alla radice cercata.

Si comincia col scegliere un numero che almeno grossolanamente possa approssimare la radice; chiamiamo questo numero x₀.

La successione di risultati x₁, x₂, x₃, ..., che si avvicinano sempre più alla radice cercata, si ottiene con la formula

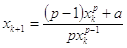A questo punto si stabilisce il numero di decimali che si vuole trovare. Quando due numeri della successione sono uguali fino al decimale stabilito, la radice è calcolata.

Esempio: si vuole calcolare 47^1/4.

Si stabilisce che sia x₀ = 2,5, perché 2⁴ fa 16 e 3⁴ fa 81, perciò la radice è un numero fra 2 e 3.

Poi si applica la formula con p = 4 e a = 47, ottenendo la formula .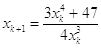

Segue il calcolo dei risultati x₁, x₂, x₃, ...; ecco i conti nei particolari:

;

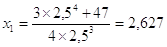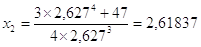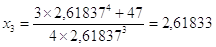I numeri della successione sono x₁ = 2,627, x₂ = 2,61837, x₃ = 2,61833, ... .

Se si stabilisce che 4 decimali sono abbastanza precisi, il risultato è 2,6183.

Esempi di uso concreto delle radici

* Per ottenere un’area quadrata di 320 cm², quanto dev’essere lungo il lato?

Indicando il lato con x, sappiamo che è 320 cm² = x²; usando la definizione di radice (quadrata), si ottiene x = (320 cm²)^1/2 = 17,89 cm.

* In 5 anni una certa popolazione di piante è raddoppiata; di quante volte cresce la popolazione all’anno?

Questo esercizio merita una spiegazione più ampia del precedente, perché è nuovo e perché è importante.

Quando una popolazione raddoppia, cresce di 2 volte. Quindi cresce di un fattore 2 (un fattore è ciò per cui si moltiplica qualcosa). Questo è ciò che è capitato durante tutto il periodo di 5 anni.

Il fattore di crescita annuo è chiaramente minore, ma non si sa quant’è, perciò lo si chiama x. Si sa soltanto che, applicando questo fattore 5 volte (cioè per i 5 anni), si ottiene il raddoppio, cioè 2. Dato che un fattore moltiplica, ciò significa che, moltiplicando x per 5 volte, si ottiene 2. O anche: la potenza quinta di x è 2.

Si ha allora 2 = x⁵; usando la radice (quinta), si ottiene x = 2^1/5 = 1,1487.

Il fattore di crescita annuo quindi è 1,1487.

* In 23 ore, lo scarto di temperatura fra un oggetto e l’ambiente si è dimezzato; di quante volte diminuisce lo scarto di temperatura all’ora?

L’esercizio è simile al precedente, ma usa le frazioni (½) o i decimali (0,5). In sostanza, si ha 0,5 = x²³, cioè x = 0,5^1/23 = 0,9703.

Si noti che, trattando numeri minori di 1, la radice (0,9703) è maggiore del radicando (0,5).

Dominio delle radici

Le radici presentano una stranezza antipatica, riassunta nelle regole che seguono.

* Se il radicando è negativo, allora l’indice può essere soltanto dispari e il risultato è negativo.

Esempi: la radice (-27)^1/3 vale -3; la radice (-5)^1/5 vale circa -1,37973; la radice (-9)^1/2 non dà risultati reali; la radice (-5)^0,623 non dà risultati reali.

* Se il radicando non è negativo, allora l’indice può essere un numero qualunque e il risultato non è negativo.

Esempi: la radice 9^1/2 vale 3; la radice 0^1/5 vale 0; la radice 8^1/3 vale 2.

Il motivo è dovuto al fatto che le radici sono l’inverso delle potenze: per la regola dei segni, se il radicando è negativo, allora è ottenuto da una potenza con base negativa ed esponente dispari (esempio: (-5)³ = -125), mentre è impossibile che sia ottenuto da una potenza positiva con esponente dispari (esempio: (-5)² = +25 e non -25!).

Quindi in tutti i passaggi di tutte le proprietà devono sempre valere le regole suddette, in particolare che, se il radicando è negativo, allora l’indice può essere soltanto dispari.

Radici da sapere

Ci sono alcune radici quadrate che vanno assolutamente sapute con grande padronanza, dato che si tratta di tabelline inverse:

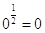
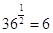
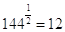
Vanno sapute anche alcune radici cubiche:

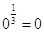
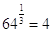
Proprietà delle radici

La radice della potenza si annulla

Mostriamo ora una proprietà essenziale della radice, cioè che radice e potenza (di uguale grado, ovviamente) si annullano fra di loro.

La radice della potenza è ;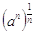

applicando la proprietà (aⁿ)^m = a^nm, si ottiene ;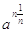

semplificando le frazioni all’esponente, si ottiene 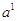, cioè a.

Tanto per capire che gli esponenti sono più comodi delle radici classiche, si dà la dimostrazione con l’uso di :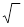

si prende la formula ;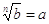

si adotta come valore di b proprio aⁿ;

sostituendo, si ottiene .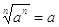

Anche in questa seconda dimostrazione ci sono 3 passaggi, ma serve più concentrazione per capirli e più sforzo per ricordarli.

In ogni caso, si arriva a 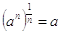, che è la proprietà da dimostrare: la radice della potenza si annulla.

Questo è uno dei punti in cui si capisce l’importanza della regola secondo cui, se il radicando è negativo, allora l’indice può essere soltanto dispari: se non valesse, sarebbero possibili giochi di prestigio come questo: -1 = [(-1)²]^1/2 = [1]^1/2 = 1, che basterebbe da solo a distruggere tutta l’aritmetica e l’algebra.

La potenza della radice si annulla

La potenza della radice è ;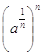

procedendo come sopra, si calcola .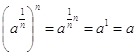

Radici di potenze, potenze di radici

Non è obbligatorio che le frazioni all’esponente abbiamo al numeratore 1; ecco perché può non essere così.

* La radice di una potenza si scrive .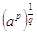

* La potenza di una radice si scrive .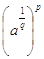

In sintesi: la scrittura 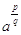indica sia una radice di potenza sia una potenza di radice: il grado della potenza è il numeratore dell’esponente, qui p, mentre l’indice della radice è il denominatore, qui q.

Esempio: in 8^7/5, all’8 bisogna applicare sia una potenza settima sia una radice quinta.

Di nuovo, se a è negativo, allora q può essere soltanto dispari. Qui la trappola da evitare è del genere -2 = (-8)^1/3 = (-8)^2/6 = [(-8)²]^1/6 = (64)^1/6 = 2. In altri termini, risulta essere -2 = 2! Dov’è l’errore?

L’errore è nel passaggio (-8)^2/6 = [(-8)²]^1/6, che non si può fare, perché -8 è negativo e 6 è pari.

Proprietà invariantiva delle radici

È .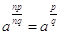

Esempio: è .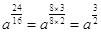

Questa proprietà, usando la notazione con gli esponenti, è particolarmente evidente: basta ridurre ai minimi termini la frazione all’esponente.

Moltiplicazione di radici con lo stesso indice

È .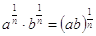

Esempio: 7^1/5´6^1/6 = 42^1/30.

Dimostrazione: si eleva alla n entrambi i membri di 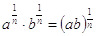è vero.

Si lascia come esercizio la dimostrazione che è .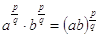

Moltiplicazione di radici con lo stesso radicando

È .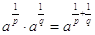

Esempio: 64^1/2´64^1/3 = 64^1/2+1/3, che fa 64^5/6. Infatti è 64^1/2 = 8, 64^1/3 = 4 e 64^5/6 = 2⁵ = 32.

Dimostrazione: si svolge il calcolo 1/p+1/q, che dà (q+p)/(pq); quindi da .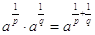

Si eleva entrambi i membri alla pq, ottenendo 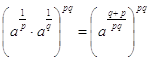è vero.

Si lascia come esercizio la dimostrazione che è .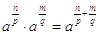

Moltiplicazione di radici in generale

È .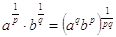

Esempio e spiegazione: volendo moltiplicare 3^1/2 per 4^1/5, si fa 3^1/2´4^1/5 = 3^5/10´4^2/10 = (3⁵)^1/10´(4²)^1/10 = (3⁵´4²)^1/10.

La dimostrazione segue lo stesso schema delle precedenti e la si lascia come esercizio.

Somma di radici: NO!!!!!!

In generale, NON è .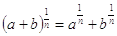

Se si vuole essere sicuri di irritare un insegnante di matematica, si può cercare di far valere questa uguaglianza in qualche calcolo, soprattutto dopo aver sentito innumerevoli volte che il passaggio è impraticabile; se si vuole aumentare l’irritazione, dopo essere stati avvisati, sempre per l’ennesima volta, che questa proprietà non vale, si può dichiarare, con aria ingenua e piuttosto sorpresa, “Davvero? Sa che mi giunge nuova?”. Purtroppo, il presente avvertimento non scongiurerà il pericolo che giunga nuova anche l’inevitabilità di un’insufficienza.

Padroneggiare le radici

Portar fuori da radice

Capita di avere radici in cui il radicando può essere ridotto, portando fuori dalla radice, con gli opportuni adattamenti, alcuni fattori; mostro come procedere mediante esempi.

Esempio A: 24^1/2 = (4´6)^1/2 = 4^1/2´6^1/2 = 2´6^1/2.

Nel caso sopra, si è scomposto il 24 in fattori, in modo che uno dei fattori fosse un quadrato (4 e 6, il 4 è un quadrato); poi si è applicata la proprietà della moltiplicazione di radici con stesso indice, isolando il quadrato; infine, il quadrato è servito per eliminare la sua radice quadrata.

Il risultato è che sotto radice ormai non c’è più il grande 24, ma soltanto il piccolo 6; il 2 non è più sotto radice.

Esempio B: 24^1/3 = (8´3)^1/3 = 8^1/3´3^1/3 = 2´3^1/3.

Qui si è ancora scomposto il 24 in fattori, ma questa volta uno dei fattori doveva essere un cubo, perché la radice è cubica. Il cubo è chiaramente 8. Così il cubo di 8 si è semplificato con la radice cubica, facendo restare 2.

In questo modo, sotto radice è rimasto soltanto un 3, invece del 24 iniziale.

Esempio C: 125^1/2 = (25´5)^1/2 = 25^1/2´5^1/2 = 5´5^1/2.

Qui si è scomposto il 125 non in un inutile 5³, ma nel più utile 5²´5. Soltanto così una sua parte è potuta uscire dalla radice.

Esempio D: 72^1/2 = (9´8)^1/2 = (9´4´2)^1/2 = 9^1/2´4^1/2´2^1/2 = 3´2´2^1/2 = 6´2^1/2.

Qui si è individuato più di un quadrato presente nel radicando. Naturalmente, era anche possibile scomporre il 72 in 36´2 e poi fare la radice di 36. Chi non riuscisse a trovare al volo questi quadrati, può sempre lavorare a tappe come ho fatto sopra, scomponendo il 72 prima in 9´8 e poi in 9´4´2.

Razionalizzare

Quando in una frazione, al numeratore o al denominatore, appaiono radici, capita che le si possa eliminare almeno dal numeratore o dal denominatore, se non addirittura dall’intera frazione. Si tratta di un modo per rendersi conto che una stessa frazione può assumere diversi aspetti.

Esempio A: si vuole togliere la radice dal denominatore in 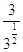. Come si nota, in questo caso felice non soltanto si è eliminata la radice al denominatore, ma si è addirittura eliminato il denominatore!

Va ammesso che in questo caso particolare, in cui l’unica base è 3, ci si poteva anche limitare all’uso delle proprietà di potenze e radici: 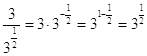. Questa seconda procedura diventa meno pratica negli esempi che seguono.

Esempio B: si vuole togliere la radice dal numeratore in .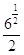

Esempio C: si vuole togliere le radici dal denominatore in .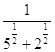

Fonte: http://schedematematica.wikispaces.com/file/view/SCHEDA%20SUI%20RADICALI%20E%20GLI%20ESPONENTI%20FRAZIONARI.doc

Autore del testo: non indicato nel documento di origine

Parola chiave google : Radicali esponenti frazionari e potenze tipo file : doc

Matematica geometria ragioneria e statistica appunti esercizi lezioni riassunti testi materiale didattico

Matematica scuola elementare , scuola media, scuola superiore e università

Matematica geometria ragioneria e statistica appunti esercizi lezioni riassunti testi materiale didattico

Radicali esponenti frazionari e potenze