Integrali

 

 

Integrali

 

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

 

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

 

 

 

 

Integrali

 

Integrale indefinito

 

Sappiamo che assegnata una funzione y = f(x) è possibile associare ad essa, sotto opportune condizioni, la sua funzione derivata . Ad esempio :

- alla funzione  y = x2  si associa la funzione derivata  y ' = 2x ;

- alla funzione  y = sin x   si associa la funzione derivata  y ' = cos x .

Ci si pone il problema inverso: data una funzione F(x) è possibile determinare una funzione f (x) tale che la derivata di questa ci fornisca la funzione F(x) , cioè tale che
f ’(x)=F(x) ?

Questo problema ha senso ; infatti , negli esempi suddetti :

- alla funzione  y = 2x  si associa   y = x2 

-alla funzione  y = cos x  si associa  y= sin x .

 

Possiamo dare allora la seguente definizione:

Data una funzione reale  y = F(x) , definita e continua in un intervallo I, si definisce primitiva della funzione  F  una funzione reale y = f(x)  tale che  f ’ = F.

 

Osserviamo però che, essendo la derivata di una costante uguale a zero , alla funzione f(x) si deve associare non una sola ma infinite primitive  f(x) + c, che differiscono per una costante additiva c. Infatti :  D( f + c) = D(f) = F .

Perciò , se  f  è una primitiva della funzione F, lo sarà anche ogni altra funzione y = f(x)+c,

con  c numero reale. L’insieme o famiglia di primitive di una funzione  F  prende il nome di integrale indefinito di  F  e si indica con il simbolo:   ∫ F(x)dx   .

Se  f  è una primitiva della  F,  si usa scrivere:  ∫ F(x)dx = f(x) + c .

L’operazione che permette di determinare le primitive di una funzione si dice integrazione indefinita e la funzione  F  si chiama funzione integranda .

L’integrazione indefinita è l'operazione inversa della derivazione.

Il problema della ricerca dell’integrale indefinito di una funzione ha una interpretazione geometrica. La famiglia di curve y =f(x) +c ha come rappresentazione grafica in un riferimento cartesiano un insieme di infinite curve, al variare di c , che sono tutte ottenibili dalla primitiva principale y =f(x) operando una traslazione di ampiezza  |c| nel senso dell’asse y . Nella traslazione, la generica retta tangente, in un punto di ascissa x , a ciascuna delle curve mantiene invariata la propria pendenza ovvero il proprio coefficiente angolare F(x) = f ’(x). Da ciò possiamo dedurre che, mentre il problema di determinare la retta tangente ad una curva in un suo punto ha una sola soluzione ( se la funzione è derivabile), il problema inverso, di determinare una curva che abbia in un suo punto come tangente una retta di assegnato coefficiente angolare, ammette infinite soluzioni.

 

Il teorema fondamentale del calcolo può così essere espresso:

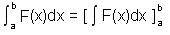intendendo, col simbolismo usato al secondo membro, la differenza fra i valori calcolati in b  e in  a  di una qualunque primitiva di F, ossia un qualunque elemento di   ∫ F(x)dx .

Proprietà dell’integrale indefinito

 

  1. L’integrale del prodotto di una costante reale per una funzione continua è uguale al prodotto della costante per l’integrale della funzione : ∫ k F(x)dx = k ∫ F(x)dx .
    Infatti derivando i due membri di tale uguaglianza si ha la funzione F e poiché si ha lo stesso risultato i due membri rappresentano la stessa primitiva.

 

  1. L’integrale di una somma di funzioni continue è uguale alla somma degli integrali delle singole funzioni:  ∫ [ F(x) + G(x) ]dx = ∫ F(x)dx + ∫ G(x)dx
    Infatti i due membri hanno la stessa derivata  F+G  e quindi sono uguali.

 

  1. L’integrale della combinazione lineare di funzioni continue è la combinazione lineare degli integrali delle singole funzioni:
    ∫ [ h F(x) + k G(x) ] dx  =  h ∫ F(x)dx  +  k ∫ G(x)dx .

 

Integrale indefinito di funzioni semplici   ( integrali immediati )

 

Sappiamo che è possibile calcolare la derivata di una qualunque funzione derivabile  direttamente attraverso il calcolo del limite del suo rapporto incrementale oppure applicando le regole di derivazione. Non è invece possibile ricavare l’integrale indefinito di una qualunque funzione continua a meno che questo non sia un integrale immediato o che ci si possa ricondurre ad esso attraverso opportuni metodi di integrazione.

Un integrale indefinito si dice immediato se nella funzione integranda si riconosce la derivata di una funzione elementare.

 

Dalle regole di derivazione si riconoscono i seguenti integrali fondamentali :

 

 

 

∫ k dx = k x + c

 

∫ x n dx  =  x n+1 / (n+1) + c     ( se  n+1 ≠ 0 )

 

∫ (1 / x ) dx  =  ln x  +  c      ( nell'intervallo  x>0 )

 

∫ (1 / x ) dx  =  ln ( - x)  +  c      ( nell'intervallo  x<0 )

 

∫ (1 / x ) dx  =  ln |x|  +  c      ( sintesi delle due precedenti )

 

∫ e x dx  =  e x  +  c

 

∫ a x dx  =  a x / ln(a)  +  c

 

∫ cos x dx = sin x + c

 

∫ sin x dx = - cos x + c

 

∫ 1 / √(1 - x2)  dx = arcsin x + c = - arccos x + c

 

∫ 1 / (1 + x2)  dx = arctg x + c

 

 

 

 

 

 
Integrazione per parti

Se f e g sono derivabili in [a,b] si ha:  ( f g ) ' = f ' g  +  f  g '

ossia:   f  g '  =  ( f g ) '  -    f ' g ..

Prendendo l'integrale indefinito di entrambi i membri ed osservando che
∫ ( f g ) ' (x)dx = f g  , a meno di una costante, si trova la formula di integrazione per parti :
∫ f (x) g ' (x) dx =  f(x) g(x) -  ∫ f ' (x) g (x) dx

da cui per gli integrali definiti :

 

 

 

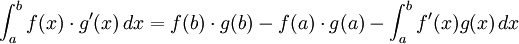
Integrazione per sostituzione

 

In alcuni casi è utile introdurre sotto il segno di integrale una variabile ausiliaria al fine di ottenere un integrale più semplice da calcolare.
Supponiamo di dover calcolare  ∫ F(x)dx .

Scelta una qualsiasi funzione derivabile con derivata continua x = g(t), con il vincolo di conoscerne anche l’inversa  t = g-1(x)=γ(x), si considera il nuovo integrale:   ∫ F[g(t)]g'(t)dt .

Se  G(t)  è una primitiva per quest’ultimo integrale, cioè qualunque sia  t  risulta: 
G’(t) = F[g(t)] g’(t),  allora la funzione composta f(x) = G[g-1(x)] è una primitiva di F.
Pertanto, se si riesce a calcolare G, si ricava  f = G ▫ h ;  se invece si riesce a calcolare  f, si ricava G = f ▫ g :

 ∫ F(x)dx = [ ∫ F [ g(t) ] g ' (t) dt  ] t=γ(x)  ,   ∫ F [ g(t) ] g ' (t) dt = [ ∫ F(x)dx ] x=g(t)        

 (di solito le scritte in pedice si sottintendono, delegando ai nomi delle variabili le relative sostituzioni finali)

ESEMPI:

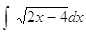
 1) Calcolare 

Poniamo   2x - 4 =  t   da cui   x =  ( t + 4 ) / 2        dx= (1/2) dt

                                                                        

 

 

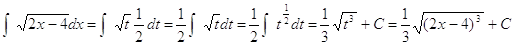
  2) Calcolare       ∫ sin5 x cos x dx

Tale integrale può anche essere espresso usando un'altra variabile: ∫ sin5 t cos t dt .
Posto x = g(t) = sin t, ricaviamo g'(t) = cos t, e quindi:

                ∫ sin5 t cos t dt  =  ∫ x5 dx = x6 / 6  + c  =  (1/6) sin6 t  + c

 

 

Fonte: http://w3.romascuola.net/gspes/materiali/integrale_indefinito.doc

Sito web da visitare: http://w3.romascuola.net/gspes

Autore del testo: non indicato nel documento di origine

Parola chiave google : Integrali tipo file : doc

 

Matematica geometria ragioneria e statistica appunti esercizi lezioni riassunti testi materiale didattico

Matematica scuola elementare , scuola media, scuola superiore e università

 

Matematica geometria ragioneria e statistica appunti esercizi lezioni riassunti testi materiale didattico

Matematica scuola elementare , scuola media, scuola superiore e università

 

 

 

 

Visita la nostra pagina principale

 

Integrali

 

Termini d' uso e privacy

 

 

 

 

Integrali