Aritmetica per bambini e ragazzi scuola elementare e prima media

 

 

 

Aritmetica per bambini e ragazzi scuola elementare e prima media

 

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

 

 

 

Aritmetica per bambini e ragazzi scuola elementare e prima media

 

L’aritmetica è la più antica branca della matematica e studia le proprietà elementari delle operazioni sui numeri. Il termine “aritmetica” deriva dalla parola greca arithmos che significa numero. La sua semplicità è dovuta dal fatto che essa è utilizzata in molte attività quotidiane dell’uomo, come per esempio contare, calcolare la spesa ecc.

 

L’aritmetica si è evoluta con l’evolversi delle esigenze di calcolo del genere umano che tra l’altro corrispondono anche alla maturazione di un individuo. Già dai primi anni, un bambino matura l’esigenza di contare e di sommare le proprie cose. I bambini piccoli, dai tre ai cinque anni, sono la massima espressione di approvvigionamento individuale, infatti, sono curiosi, voglio tutto e voglio sapere tutto. Provate a chiedere ad un bambino di tre anni se vuole una caramella, quasi certamente risponderà che ne vuole due. Quindi inizialmente si imparano i numeri naturali e la loro somma. Subito dopo, contemporaneamente all’amicizia nasce nel bambino una componente altruistica, cioè sottrae qualcosa dai propri averi per donarla agli amici, così sviluppa anche un senso di mancanza e di privazione. Ed ecco la nascita dell’operazione di sottrazione dei numeri naturali e la nascita dei numeri relativi nei quali si contemplano anche i numeri negativi. La generosità e la condivisione aumentano col crescere, si dividono i frutti conquistati con la collaborazione e anche una sola caramella va divisa. Ed ecco nascere infine le divisioni e le frazioni.

 

Questa lezione non richiede quindi un impegno eccessivo, i contenuti saranno acquisiti con molta naturalezza nella maggioranza dei casi.

 

«

 

Nel precedente argomento (Cenni di Insiemistica) abbiamo introdotto i principali insiemi numerici e le loro relative operazioni, quelle ben definite e non. Cercheremo ora di capire meglio che qualsiasi operazione ben definita è anche un’operazione interna, mentre non lo è un’operazione non ben definita.

 

Generalmente in matematica, un’operazione è una qualsiasi azione che se applicata su una coppia di elementi di un dato insieme detti operandi, questa produce un elemento detto risultato dell’operazione. A questo punto occorre fare un’importante considerazione, e cioè, se il risultato appartiene all’insieme di base (l’insieme al quale appartengono gli elementi su cui è stata applicata l’operazione), allora l’operazione si dirà operazione interna, altrimenti, tale operazione si dirà operazione esterna.

 

Questo concetto di operazione interna vale per qualsiasi sia la natura degli elementi, infatti, può valere anche per le figure geometriche. Ad esempio, proviamo a verificare se la seguente operazione tra elementi geometrici è un’operazione interna:

 

• Consideriamo un insieme a cui appartengono i segmenti di tutte le lunghezze; (Insieme di base)

 

• Consideriamo come operazione la somma di due segmenti;

 

• Il risultato di tale operazione, cioè della somma dei due segmenti, è rappresentato da un terzo segmento lungo quanto i primi due messi insieme.

 

É facile verificare che questa è un’operazione interna, infatti, per qualsiasi coppia di segmenti iniziali, il risultato sarà un segmento di una certa lunghezza e quindi appartenente all’insieme di base.

 

Fonte: http://www.atuttoportale.it/didattica/a_scuola_di_matematica/Argomento-02.doc

Sito web da visitare: http://www.atuttoportale.it/

Autore del testo: Amitrano Eugenio

Parola chiave google : Aritmetica per bambini e ragazzi scuola elementare e prima media tipo file : doc

 

Aritmetica per bambini e ragazzi scuola elementare e prima media

Addizione, sottrazione, moltiplicazione, divisione…?

Quale operazione?

 

 

Il linguaggio dell’addizione

 

 

Il linguaggio della moltiplicazione

 

 

 

 

 

 

 

 

  

  

 

 

 

Fonte: http://www.melzoscuole.gov.it/old/download/docenti/matematica3/parole-chiave_nei_problemi.doc

Sito web da visitare: http://www.melzoscuole.gov.it

Autore del testo: non indicato nel documento di origine

Parola chiave google : Aritmetica per bambini e ragazzi scuola elementare e prima media tipo file : doc

 

Aritmetica per bambini e ragazzi scuola elementare e prima media

O P E R A Z I O N I     NELL’ INSIEME  DEI   NUMERI    NATURALI       N

 

1)         ADDIZIONE    e   PROPRIETA’

 

L’addizione è l’operazione con la quale si ottiene la somma di due numeri.

I numeri si dicono addendi e il risultato si dice somma o totale .

L’addizione è sempre possibile in  N , per questo si dice operazione interna ad N.

 

PROPRIETA’

 

COMMUTATIVA	a+b = b+a	5+1 = 1+5
ASSOCIATIVA	a+b+c = (a+b)+c	7+3+8 = (7+3)+8
DISSOCIATIVA	a+b+c = ( a1+a2) +b+c	7+5+9 = (4+3)+5+9
ELEMENTO NEUTRO	a+0 = 0+a = a	3+0 = 0+3 = 3

 

2)         SOTTRAZIONE    e   PROPRIETA’

 

La sottrazione è l’operazione con la quale si ottiene la differenza o resto tra due numeri e si scrive a - b = c ;   a si dice minuendo e b è il sottraendo .

Precisamente : la differenza tra due numeri   a , b con   a ³ b è quel numero c che sommato al sottraendo , dà il minuendo.

La sottrazione  non è sempre possibile in  N , lo è solo quando il minuendo è maggiore del sottraendo.

La sottrazione è l’operazione inversa dell’addizione .

 

PROPRIETA’

 

INVARIANTIVA

a-b = (a+m)-(b+m) a-b = (a-m)-(b-m)

= (15+2) - (8+2) 9-3 = ( 9-1)- (3-1)

 

3)         MOLTIPLICAZIONE    e    PROPRIETA’

 

La moltiplicazione è l’operazione con la quale si ottiene il  prodotto di due numeri : a .b = c.

Il prodotto  a .b  è la somma di tanti addendi uguali ad a , quante sono le unità di b

I numeri  a e b si dicono fattori  e il risultato si dice prodotto.

La moltiplicazione è sempre possibile in  N , per questo si dice operazione interna ad N.

 

PROPRIETA’

 

COMMUTATIVA	a .b = b .a	5.3 = 3.5
ASSOCIATIVA	a. b. c = (a .b).c	7.3.8 = (7.3).8
DISSOCIATIVA	a .b .c = ( a1.a2) .b .c	6.5.9= (2.3).5.9
DISTRIBUTIVA rispetto all’ADDIZIONE	a .(b + c ) = a .b +a .c	3.( 4+5) = 3 .4 + 3.5
DISTRIBUTIVA rispetto alla SOTTRAZIONE	a .(b - c ) = a .b - a .c	3.( 4- 5) = 3 .4 -  3.5
ELEMENTO NEUTRO	a .1 = 1 . a = a	3.1 = 1.3 = 3
	a . 0 = 0 . a = 0
Legge di Annullamento del Prodotto	a .b = 0   «   a = 0 , oppure b = 0 , oppure   a = b = 0

 

4)  DIVISIONE    e    PROPRIETA’

 

La divisione è l’operazione con la quale si ottiene il quoziente o quoto tra due numeri e si scrive

 a : b = c ;   a si dice dividendo  e b è il divisore .

Precisamente : il quoziente  tra due numeri   a , b con    b  ¹ 0   è quel numero c che moltiplicato per il divisore b , dà come risultato a .

La divisione esatta ( cioè con resto zero) non è sempre possibile in  N , lo è solo quando il numero a è multiplo di  b  .

La divisione è l’operazione inversa della moltiplicazione.

 

PROPRIETA’

 

INVARIANTIVA	a : b = (a .m) : (b .m) a : b = (a :m) : (b : m)	20 : 2 = (20 .3 ) : ( 2 .3 ) 20 : 4 = (20 : 2) : (4 : 2 )
Altre proprietà	a : a = 1  ;  a : 1 = a
	0 : b =  0
	a : 0 = impossibile
	0 : 0 = indeterminata

 

O P E R A Z I O N I     NELL’ INSIEME  DEI   NUMERI  INTERI  RELATIVI  Z

 

E   RAZIONALI  RELATIVI  Q  

 

• Numero Intero Relativo : è ogni numero naturale preceduto dal segno + o - .
• Numero Razionale  Relativo : è ogni numero razionale assoluto ( frazione )  preceduto dal segno + o - .
• Valore Assoluto o Modulo di un numero relativo a : si indica con  | a |

             ed è uguale ad  a , se a ³ 0 ;  è uguale   all’opposto di a , cioè – a , se a < 0

• Due o più numeri  relativi diversi  da  0  si dicono :
• Concordi , se hanno stesso segno
• Discordi , se hanno segno diverso
• Uguali , stesso segno e stesso valore assoluto
• Opposti , se sono discordi , cioè hanno segno diverso , ma lo stesso valore assoluto.

 

1)         ADDIZIONE  in   Z  e in Q    e  PROPRIETA’

 

L’addizione è sempre possibile in  Z e in Q , per questo si dice operazione interna .

 

PROPRIETA’

 

COMMUTATIVA	a+b = b+a	5+1 = 1+5
ASSOCIATIVA	a+b+c = (a+b)+c	7+3+8 = (7+3)+8
DISSOCIATIVA	a+b+c = ( a1+a2) +b+c	7+5+9 = (4+3)+5+9
ELEMENTO NEUTRO	a+0 = 0+a = a	3+0 = 0+3 = 3
ELEMENTO SIMMETRICO	a + ( - a ) = ( - a ) + a  = 0

 

 

2)         SOTTRAZIONE    e   PROPRIETA’

 

La sottrazione  è sempre possibile in  Z e in Q.

 

PROPRIETA’

 

INVARIANTIVA

a-b = (a+m)-(b+m) a-b = (a-m)-(b-m)

= (15+2) - (8+2) 9-3 = ( 9-1)- (3-1)

 

3)         MOLTIPLCAZIONE    e    PROPRIETA’

 

La moltiplicazione è sempre possibile in  Z e in Q .

 

PROPRIETA’

 

COMMUTATIVA	a .b = b .a	5.3 = 3.5
ASSOCIATIVA	a. b. c = (a .b).c	7.3.8 = (7.3).8
DISSOCIATIVA	a .b .c = ( a1.a2) .b .c	6.5.9= (2.3).5.9
DISTRIBUTIVA rispetto all’ADDIZIONE	a .(b + c ) = a .b +a .c	3.( 4+5) = 3 .4 + 3.5
DISTRIBUTIVA rispetto alla SOTTRAZIONE	a .(b - c ) = a .b - a .c	3.( 4- 5) = 3 .4 -  3.5
ELEMENTO NEUTRO	a .1 = 1 . a = a	3.1 = 1.3 = 3
	a . 0 = 0 . a = 0
Legge di Annullamento del Prodotto	a .b = 0   «   a = 0 , oppure b = 0 , oppure   a = b = 0
Regola dei segni : Il prodotto di 2 numeri concordi ha sempre segno +   ;   Il prodotto di 2 numeri discordi ha sempre segno – Il  prodotto di più fattori ha segno  + , se il numero dei fattori negativi è PARI; Il prodotto di più fattori ha segno  - , se il numero dei fattori è DISPARI

 

 

4)  DIVISIONE    e    PROPRIETA’

 

La divisione esatta ( cioè con resto zero) non è sempre possibile in  Z , lo è solo quando il numero a è multiplo di  b  .Invece è sempre possibile in Q .

La divisione è l’operazione inversa della moltiplicazione.

 

PROPRIETA’

 

INVARIANTIVA	a : b = (a .m) : (b .m) a : b = (a :m) : (b : m)	20 : 2 = (20 .3 ) : ( 2 .3 ) 20 : 4 = (20 : 2) : (4 : 2 )
Altre proprietà	a : a = 1  ;  a : 1 = a
	0 : b =  0
	a : 0 = impossibile
	0 : 0 = indeterminata

 

 

Fonte: http://www.bassilo.it/documents/MFIOCCHI/Toperazioni%20e%20proprieta.doc

 

Autore del testo: non indicato nel documento di origine

Parola chiave google : Aritmetica per bambini e ragazzi scuola elementare e prima media tipo file : doc

 

Aritmetica per bambini e ragazzi scuola elementare e prima media

Sintesi

Numeri

Alla base di tutte le conoscenza scientifiche vi sono i numeri. 

I numeri fondamentali sono i numeri naturali 1, 2, 3, ... Gli altri tipi di numeri si definiscono a
partire dai numeri naturali.

I numeri naturali sono entità indefinibili. Sono dati "a priori" come oggetti di cui abbiamo tutti 
innata intuizione. Tutti li usiamo ma nessuno può affermare cosa essi siano senza cadere nella 
ovvia tautologia "i numeri naturali sono i numeri naturali".

Nel linguaggio scientifico, quando qualcosa, un concetto, una affermazione, non è spiegabile
in termini logici a partire da altri concetti, affermazioni ecc. si dice che quel qualcosa è un
assioma, un postulato. Le altre affermazioni che sono derivabili logicamente da altre
affermazioni si chiamano invece teoremi.

Le regole logiche che si utilizzano per dimostrare un teorema a partire da altri postulati o
teoremi sono in definitiva le regole del "buon senso", quelle che non producono contraddizione.

Senza addentrarci nei particolari (la logica matematica è una branca della matematica a sé stante),
diamo solo alcuni esempi di queste regole logiche :

      - 1 - una affermazione può essere o vera o falsa (legge del terzo escluso)

      - 2 - se l'affermazione A implica l'affermazione B, allora la negazione di B implica la negazione
              di A (legge di contrapposizione)

      - 3 - se l'affermazione A implica l'affermazione B e l'affermazione B implica l'affermazione C,
              allora A implica C (legge transitiva)

Noi usiamo le regole della logica ogni momento della nostra vita, quando pensiamo o parliamo,
anche se non ne siamo consci. 

Proseguiamo ora con la descrizione delle proprietà dei numeri naturali e degli altri tipi di numeri.

01 - Numeri naturali.

Come abbiamo sopra affermato i numeri naturali sono : 1, 2, 3, ... e non possono essere definiti o
spiegati ulteriormente. Essi sono dati a priori. Si noti che il numero 0 non appartiene ai numeri
naturali.

Le caratteristiche principali dei numeri naturali sono :

      - 1- ogni numero naturale possiede un numero naturale "successivo". Per esempio se prendo
             il numero 12, il suo successivo è 13.

      - 2 - ogni numero naturale è ottenibile partendo dal numero 1 "contando" in successione.

Questi fatti, anch'essi non dimostrabili, sono di fondamentale importanza perché permettono di
definire l'operazione di addizione fra due numeri naturali per ottenerne un terzo.

Il successivo di un numero naturale può essere considerato come la somma del numero dato
più il numero 1 :

      12 + 1 = 13

La somma di due numeri naturali qualunque può essere di conseguenza ottenuta partendo dal primo
addendo e "contando" tutti i numeri successivi per un numero di volte corrispondente al secondo addendo :

      4 + 3  = (((4 + 1) + 1) + 1) = 7

Anche l'operazione di moltiplicazione è riconducibile all'operazione di addizione. Infatti, per esempio :

      2 * 3 = 2 + 2 + 2

ovvero moltiplicare due numeri naturali significa sommare il primo fattore a sé stesso per un numero
di volte pari al secondo fattore.

Abbiamo così ricostruito le regole dell'aritmetica elementare partendo da pochissimi assiomi : l'esistenza
dei numeri naturali (addirittura è sufficiente ipotizzare l'esistenza del solo numero1), la possibilità
di determinare il successivo di ogni numero naturale e la possibilità di contare in successione.

02 - Numeri interi.

La definizione di addizione fra numeri naturali ci permette di definire una nuova operazione : la sottrazione.

La sottrazione fra due numeri naturali è l'operazione inversa dell'addizione. Per esempio :

      5 - 2 = 3   in quanto  5 = 2 + 3.

Sorge a questo punto un problema. Se il primo termine della sottrazione è minore del secondo
la sottrazione è impossibile in quanto non vi è nessun numero naturale che possa essere il risultato
di simile operazione. Per esempio :

      2 - 5 = impossibile, in quanto non esiste nessun numero naturale che sommato a 5 dia 2.

Se però introduciamo il numero 0 ed i numeri interi negativi -1, -2, -3 ... ogni operazione di 
sottrazione di numeri naturali diventa possibile. Esempi :

      5 - 2 = 3   
      2 - 5 = -3  perché  2 = 5 - 3 
      3 - 3 = 0   perché  3 = 3 + 0

L'insieme di numeri naturali con l'aggiunta dello 0 e dei numeri interi negativi forma così un nuovo 
insieme di numeri che è una estensione dell'insieme dei numeri naturali : questo nuovo insieme si
chiama insieme dei numeri interi.

All'interno dei numeri interi possiamo eseguire le operazioni di somma, sottrazione e moltiplicazione.

03 - Numeri razionali.

La definizione di moltiplicazione fra numeri interi ci permette di definire una nuova operazione : la divisione.

La divisione fra due numeri interi è l'operazione inversa della moltiplicazione. Per esempio :

      10 : 2 = 5   in quanto  10 = 2 * 5.

Sorge a questo punto un problema. Se il primo termine della divisione non è multiplo del secondo
la divisione è impossibile in quanto non vi è nessun numero intero che possa essere il risultato
di simile operazione. Per esempio :

      10 : 3 = impossibile, in quanto  non esiste nessun numero intero che moltiplicato per 3 dia 10.

Se però introduciamo le frazioni positive e negative ... 1/2, -2/3 ... ogni operazione di divisione di
numeri interi diventa possibile. Esempi :

      10 : 2 = 5   
      10 : 3  = 10/3  perché  10 = (10/3) * 3 
      (-2) : 3 = -2/3   perché  -2 = (-2/3) * 3
      (-2) : (-3) = 2/3   perché  -2 = (2/3) * (-3)

L'insieme di numeri interi con l'aggiunta delle frazioni positive e negative forma così un nuovo
insieme di numeri che è una estensione dell'insieme dei numeri interi : questo nuovo insieme si
chiama insieme dei numeri razionali.

All'interno dei numeri razionali possiamo eseguire le operazioni di somma, sottrazione, moltiplicazione
e divisione .

04 - Numeri reali.

I numeri razionali dotati delle usuali quattro operazioni non sono gli unici numeri che possiamo costruire.
Già i matematici greci verificarono che esistevano altri tipi di numeri, i cosiddetti numeri irrazionali, cioè 
che non possono essere riconducibili ai numeri razionali, ovvero frazioni di numeri interi. 

I numeri irrazionali sono infiniti. Ad essi appartengono per esempio 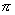(radice quadrata 
di 2). 

. 

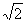I numeri irrazionali si possono allora rappresentare come numeri decimali ad infinite cifre non periodiche
dopo la virgola. 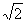 risulta allora uguale a 1,41421... 

L'insieme di tutti i numeri razionali e di quelli irrazionali si chiama l'insieme dei numeri reali. Su di essi si possono
effettuare le usuali quattro operazioni.

05 - Numeri complessi.

Oltre ai numeri reali si possono costruire i numeri complessi a partire dall'unità immaginaria .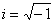

La radice quadrata di -1 non è fattibile nel campo dei numeri reali in quanto non esiste nessun numero
reale che moltiplicato per sé stesso dia -1. 

L'introduzione del numero immaginario  i  permette invece di estendere i numeri reali e l'insieme che 
se ne ottiene si chiama l'insieme dei numeri complessi. 

Ogni numero complesso si definisce come somma di un numero reale più un altro numero reale 
moltiplicato per  i , ovvero :

      z = x + y i .

Sull'insieme dei numeri complessi di essi si possono effettuare le usuali quattro operazioni.

 

Fonte: http://www.alessandrobonini.it/download/matematica/Sintesi-numeri.doc

 

Autore del testo: non indicato nel documento di origine

Parola chiave google : Aritmetica per bambini e ragazzi scuola elementare e prima media tipo file : doc

 

Matematica geometria ragioneria e statistica appunti esercizi lezioni riassunti testi materiale didattico

Matematica scuola elementare , scuola media, scuola superiore e università

 

Aritmetica per bambini e ragazzi scuola elementare e prima media

 

 

 

 

Visita la nostra pagina principale

 

Aritmetica per bambini e ragazzi scuola elementare e prima media

 

Termini d' uso e privacy